石墨烯纳米片大自旋特性第一性原理研究∗

张淑亭 孙志 赵磊

(哈尔滨理工大学电气与电子工程学院,工程电介质及其应用教育部重点实验室,黑龙江省电介质工程重点实验室,哈尔滨 150080)

1 引 言

石墨烯被公认为是下一代电子和自旋电子器件的基础材料,其独特的磁性能使碳基材料的磁学研究受到了广泛关注[1,2].二维石墨烯晶体的发现引起了对石墨烯体系的深入研究,很多特殊的性质如无质量准粒子、高迁移率和相干性、室温量子霍尔效应以及半金属性等不断被发现,对于基础理论和技术应用都有重要意义[3−7].目前大多数石墨烯的研究都集中在和电子电导率有关的介观特性上,只有少数研究特别关注于石墨烯衍生结构如石墨烯纳米带(GNR)的内禀磁性[8−11].GNR的锯齿形边缘产生的边缘局域态使费米能级附近的电子能带结构趋于平坦,通过自旋极化形成反平行自旋排列而使总的自旋为零[10,11].一维结构的GNR具有平直的边缘,可以被看作在两个维度上都为有限尺度的任意形状石墨烯纳米片(GNF)的一种特例.掌握GNF的特殊性质,使其应用于电子和自旋器件的基本功能组件,能够在纳米尺度上仍然保持器件微型化发展趋势(摩尔定律).最近的实验研究已经能够在数十纳米的尺度上探测石墨烯的特征属性,同时量子限制作用和边缘变化使GNF呈现丰富的电子和磁特性[12],但已经报道的GNR磁性研究只涉及到关于GNF磁应用的一小部分.

本文通过第一性原理电子结构计算和苯环形图理论(benzenoid graph theory)研究任意形状的边缘氢化GNF的磁学性质,包括3次和6次旋转对称类型以及其他的一些与有限GNR相关的纳米片几何结构,图1为各种GNF的形状结构示意图.除了图1(c)表示的锯齿边缘三角形GNF结构具有随尺寸线性增大的拓扑挫折净自旋,其他5种形状GNF的内禀自旋都为零.本文还探讨了运用拓扑挫折原理设计大自旋结构,应用于自旋电子器件.

在某些特殊拓扑结构的分子或原子体系中,电子的能量矩阵成为奇异矩阵即具有能量本征值为零的电子成键状态,被称作非键态(NBS),发生所有π键都不能满足量子力学条件的拓扑挫折,会产生由费米能级简并导致的单电子占据自旋排列分子轨道(SOMO),对应的特殊原子结构称作奇异分子图(singular molecular graph).如何表征奇异图一直是形图理论中的一个未解决的问题,虽然1985年第一次实现了苯环结构奇异图的结构标定,但直到20年后才建立起严格的定理来描述原子结构特征与电子能量本征值分布的关联性[13,14].对于由苯环构成的GNF,这一定理表明奇异图的成对非相邻顶点和边缘的最大数量a和b满足条件a=b+z和b=p=q,其中p,q和z分别表示电子能量本征值为负值、正值和零的数量,能量本征值为零的本征态即为NBS.因此奇异图体系的总自旋为S=z/2=(a−b)/2=a−n/2,其中n=p+q+z表示顶点总数量.由双六角苯环晶格单元构成的GNF根据对称性分成两组间隔成键相邻排列的碳原子位点,即成键的相邻两个碳原子属于不同组A和B,如图1所示.GNF的两个子晶格之间通过化学键相连,但子晶格内部各格点之间都不是化学键相连的近邻原子,一般满足nA,nB6a(nA和nB分别表示两个子晶格A和B的格点数),在特殊情况下满足a=max{nA,nB},如图1示意的所有GNF结构都属于这种情况[15].据此,通过将GNF裁割成子片段并逐个拼接的方法能够分析计算NBS总数z:拼接子片段时根据子片段交界线上碳原子数的奇偶性累计NBS数量,偶数时NBS不变,奇数时增加一个NBS.按照这样的构造计算法则,可以通过拼接自旋为零的碳六角单元组合来构建净自旋不为零的GNF,最简单的例子就是由单苯→双苯→三角三苯逐个拼接可获得自旋为0.5的最小GNF.在锯齿边缘三角形GNF的一条边上增加一层苯环使边缘碳原子数增加了1个且仍然保持三角形状,由于新增加的A和B碳原子格点数相差1(如图1(c)),所以引入了比A格点数更多的1个B格点.根据形图定理,每增加一层边缘碳原子后,锯齿边缘三角形GNF的NBS总数就增加1个(净自旋增加0.5),NBS总数z=N−1(N为边缘碳原子数),因此锯齿三角形GNF的净自旋随着纳米片半径尺寸线性增加.相比之下,无论是何种边缘类型,GNR的NBS数都为零,因为在GNR结构中A和B格点碳原子总是成对出现(如图1(a)和图1(b)).因此GNR电子能带的平缓带边是由尺度效应造成的,而GNF的NBS在费米能级附近的高度简并来自于电子能量矩阵的奇异性,二者的根本区别导致GNR没有自旋而GNF却能够形成很大的净自旋.

图1 由不同原子排列边缘扩展而成的各类GNF形状结构示意图(未显示末端氢原子) (a)锯齿形边缘GNR;(b)扶手椅形边缘GNR;(c)锯齿形边缘三角GNF;(d)扶手椅形边缘三角GNF;(e)锯齿形边缘六方GNF;(f)扶手椅形边缘六方GNFFig.1.Various types of GNF extending from smaller edges(darker shade)with different atomic alignments.The hydrogen termination along the edges is not shown for clearity:(a)Zigzag-edged GNR;(b)armchair-edged GNR;(c)zigzag-edged triangular GNF with four edge carbon atoms;(d)armchair-edged triangular GNF;(e)zigzagedged hexagonal GNF with three edged carbon atoms;(f)armchair-edged hexagonal GNF.

2 理论方法

为了进一步证实由形图理论推出的GNF自旋特性,按照基于自旋密度泛函理论的全电子数值轨道第一性原理方法,使用Materials Studio 8.0软件包中的DMol3模块计算GNF的原子结构、能量和电子结构[16,17].采用广义梯度近似的PBEsol交换相关泛函[18].电子本征态波函数由双数值极化基组展开,总轨道截止(global orbital cuto ff)设为5.0 Å使得引入的有限基组误差足够小.电子与原子实相互作用由全电子相对论(all electron relativistic)核处理(core treatment)来描述.自洽场迭代的收敛容忍度设为1.0×10−6Ha/atom(1 Ha=27.2 eV).基于狄拉克相对论量子力学方程组的自旋密度泛函理论,对不同自旋的电子采用不同本征态波函数,计算自旋-轨道相互作用和自旋极化[19].通过基于共轭梯度法的总能量最小化对GNF的原子结构进行几何优化[20],以获得低于1.0×10−5Ha/atom的总能量收敛性,并且使作用于原子上的力和原子位移分别小于0.002 Ha/Å和0.005 Å,从而获得弛豫的原子结构.

3 结果与讨论

电子之间的交换作用要求相同能量的电子本征态的自旋最大化(类似于原子轨道的洪德规则),而NBS处于由同一自旋状态电子填充的半满状态,类似于铁磁原子的电子外壳层,所以未形成自旋极化的GNF处于自旋不稳定状态.因此,为了探讨自旋极化的作用,用类似的第一性原理方法进行非自旋极化的电子结构计算并进行比较.第一性原理计算结果表明边长N=6的锯齿边缘三角形GNF中简并的NBS因自旋极化发生分裂,产生0.70 eV的带隙和自旋值为2.50的净自旋,如图2(a)所示.自旋极化状态的基态能量低于非自旋极化基态能量0.58 eV.在自旋极化分裂成的两种电子自旋态中数量较多的自旋态(上旋)局域分布在数量较多的子晶格A的碳原子上(如图2(b)).自旋极化轨道的非自旋对称性使简并的深能级轨道发生分裂(如图2(a)).由于两种自旋态在空间上的非对称分布,上旋轨道附属于数量较多的子晶格A上,而下旋电子被限制在数量较少的子晶格B上(如图2(b)),因此由两个子晶格上自旋相反的自旋极化态形成了亚铁磁有序,且净自旋来自分布于A格点上的NBS(如图2(c)).在锯齿边缘三角GNF中总上旋电子数大于总下旋电子数产生的净自旋数为(N−1)/2,随GNF的线性尺度呈正比增加,与形图理论得出的结果相一致.

锯齿边缘三角形GNF中的NBS由自旋极化在费米能级处产生的能带带隙0.4—0.7 eV(如图3中Emin所示),因此电子将在室温下仍然保持比较稳定的自旋排列,与sp电子高温磁性理论研究结果相一致[21].当三角形GNF的线性尺寸超过了纳米尺度(N>13),电子能带带隙减小至接近于零,对应于二维石墨烯的狄拉克点,但SOMO最低能级与最低未占据轨道(LUMO)能级之差(图3中定义为Emax)保持在∼0.68 eV,因此即使GNF的尺寸超过了纳米尺度,在室温下三角形GNF边缘仍然保留一部分磁矩(所有SOMO自旋电子能够被激发才会完全失去净自旋).石墨烯中电子的弱自旋-轨道耦合和超精细相互作用导致自旋态的相干时间显著增加[22,23],加上随尺度增加的净自旋在室温下的稳定性,能够通过纳米石墨烯制作纳米反铁磁体并有望应用于自旋电子器件如自旋存储器、晶体管和固态量子位元等.

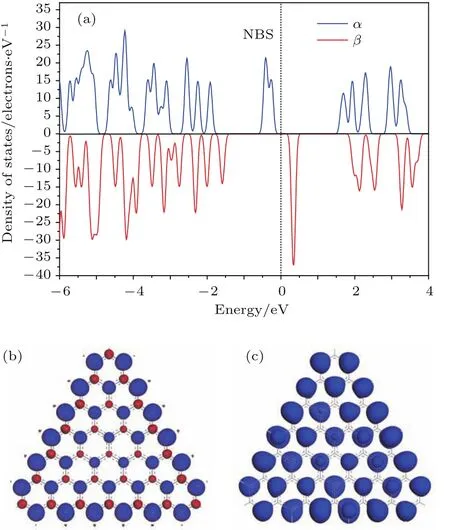
图2 锯齿型边缘三角GNF的净自旋和亚铁磁有序 (a)自旋态密度(正负曲线分别表示电子α-上旋和β-下旋态),高斯拖尾宽度0.05 eV,竖直虚线表示费米能级(参考能量零点);(b)全部电子占据轨道;(c)NBS的自旋密度空间分布——等自旋密度面(蓝色和红色分别表示上旋和下旋态,等密度值为0.02/Å3)Fig.2. Zigzag-edged triangular GNF with ferrimagnetic order and linearly scaling net spin represented as:(a)Density of spin states with up and down panels identifying up and down spins respectively,Gaussian smearing 0.05 eV,vertical dot line indicates Fermi energy level(reference energy zero);(b)all occupied orbitals;(c)NBS spin density distributions illustrated as isosurfaces of spin density with the blue and red colors indicating the up and down spins respectively,contoured at the value of 0.02/Å3.

从化学角度来看,边缘由氢钝化的三角形GNF可以被当作巨大的碳氢自由基,只不过不具有普通自由基的活性,因为在π键共轭体系中未成对电子自旋轨道的离域化使能量显著降低,已有理论研究证明小尺寸石墨烯体系和GNR确实具有较高的稳定性[24,25].化学合成稳定的大自旋聚合物自由基一直是一个长期目标,目前一些实验研究已经成功地制备了具有超高自旋输运和载流子迁移率性能的大共轭π键聚合物[26].但是用传统的化学方法合成大自旋分子受到复杂反应路径的限制,并且苛刻的化学反应条件和自由基之间的相互作用很容易破坏分子的自旋特性.相比之下,大自旋GNF可以用光刻技术雕琢石墨烯来制作,因而避免了化学合成中的复杂问题.本文的形图理论分析和第一性原理计算结果证明亚微米尺寸GNF的净自旋值很容易超过已经报道的共轭聚合物所能达到的最高自旋值,得出的结论与Ezawa[27],Fernndez-Rossier和Palacios[28]及Hod 等[29]对长方形、三角形和六边形GNF的研究结果相一致.尽管在实际GNF中可能存在的晶格缺陷会降低净自旋,但是根据形图理论缺陷对总自旋的影响较小,少量缺陷不至于破坏GNF边缘的规则性.

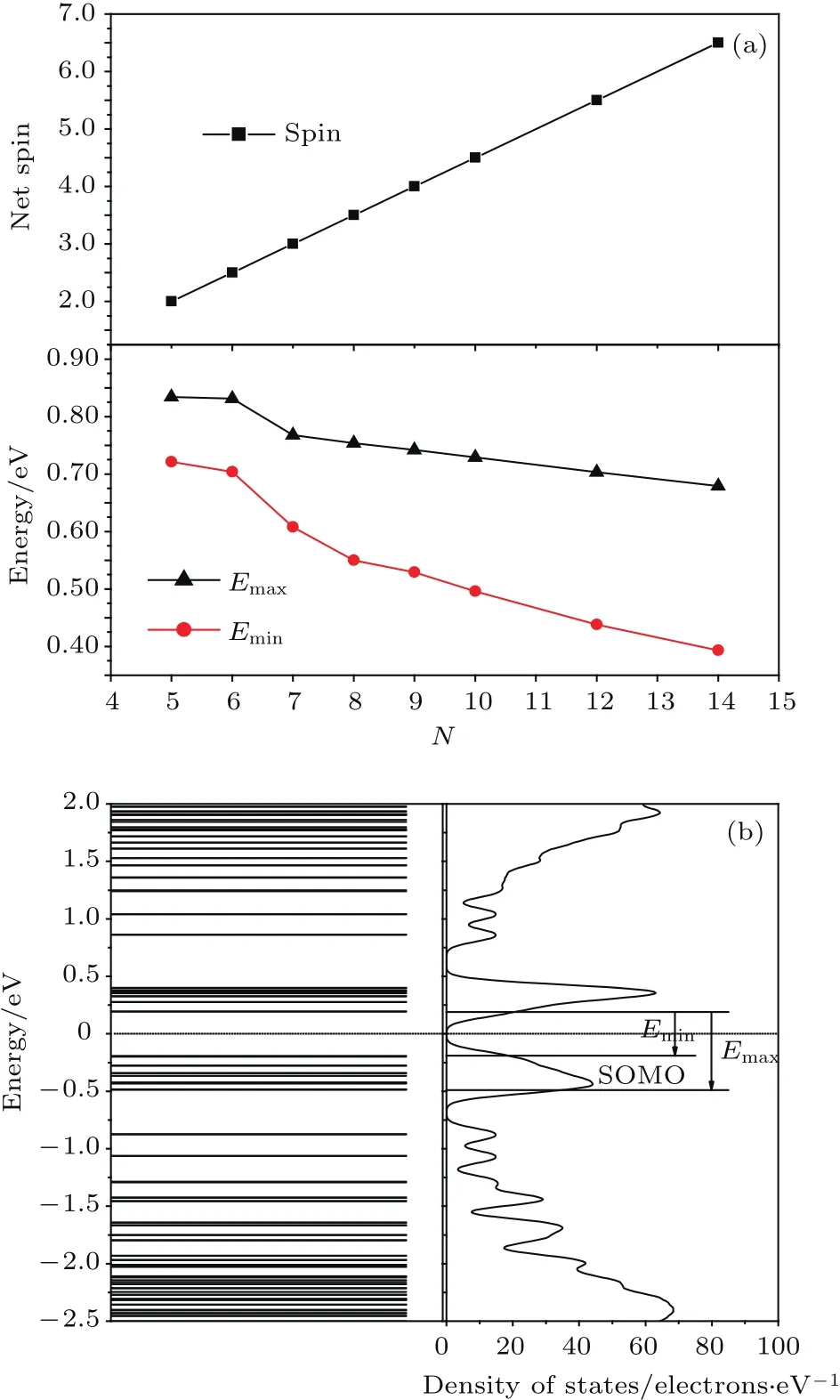
图3 (a)自旋值和能带带隙随锯齿形边缘三角GNF线性尺度N(边缘碳原子数)的变化;(b)电子轨道能谱和态密度,高斯拖尾宽度0.05 eV.Emax和Emin分别表示SOMO最低和最高能级到LUMO能级的能量差Fig.3.(a)Spin values and energy gaps scaling with the inverse linear size N(edge carbon atom number)of zigzag-edged triangular GNF;(b)orbital energy spectrum and density of states for N=14,with Gaussian smearing 0.05 eV and indicating the maximum Emax and minimum Eminenergy gaps from the lowest and highest levels of SOMOs to LUMO respectively.

根据形图理论,具有大自旋的锯齿形边缘三角GNF只是满足NBS条件的一种特殊情况,在一些非近邻顶点数不等于nA或nB的GNF仍然可以具有NBS并更有效地呈现较大的净自旋,例如由在相反方向上连续重叠连接的三角形GNF构成的分形结构-David星形GNF以及更高一级的分形结构,如图4(a)和4(b)所示.David星形GNF中由A和B子晶格组成的成对非相邻顶点碳原子组间隔出现在六个星角区(如图4(a)所示),因此即使是A和B子晶格的碳原子数相同,成对非相邻顶点数a仍然明显高于原子总数的一半,使NBS总数及净自旋与星角数量成正比.第一性原理计算David星形GNF的总自旋为2.50,带隙宽度为0.16 eV,与形图理论得出的结果相一致,本质上是由于分形结构边界长度的增加有效提高了共轭π键发生拓扑挫折的概率.该分形结构的维度为log(1/6)/log(1/3)=1.62(连续两级自相似形的原子数比例为1/6,线性尺寸比例为1/3),因此总的星角顶点数及自旋值St随分形结构的自相似维度l和分形级数m呈指数增加:St=2.5×2ml.

另一种能产生拓扑挫折并可形成多样磁有序的典型GNF结构如图5所示,由锯齿边缘三角GNF通过锯齿边缘GNR结合而成,其中三角形GNF顶点所属子晶格种类由GNF与GNR连接方式决定.由于GNR的费米能级处于能带中间(无带隙),具有良好的导电性,该结构可用于制作电子和自旋电子电路元件.DMol3第一性原理计算的结果表明,在锯齿边缘GNR上引入锯齿边缘三角形GNF所产生的净自旋密度主要局限在三角形GNF突出边缘并有一部分扩展到GNR的另一边(如图5(a)所示),净自旋值为2.00,自旋极化分裂带隙为0.52 eV.此外,中间镂空锯齿形三角形的GNF也能形成较大净自旋(如图5(b)所示),净自旋值为1.00,自旋极化分裂带隙为0.42 eV.这两类拓扑结构的GNF产生净自旋的机理与锯齿三角形GNF相同,都是因为A和B格点数不相等破坏了格点的反演对称性.GNF产生大自旋的多样性和设计灵活性使其很有希望用作自旋存储和自旋过滤器件.从理论上讲,采用电子束或扫描探针显微刻蚀方法,通过雕刻单层石墨烯能够制作由GNF元件构成的纳米自旋电子电路.

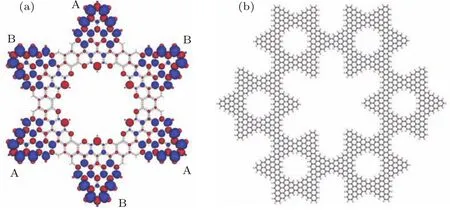
图4 (a)David星GNF的自旋密度等值面分布,蓝色和红色分别表示上旋和下旋态,自旋等密度面的密度值为0.003/Å3,A和B标示分别属于两套石墨烯子晶格的上自旋态高密度区域;(b)以David星GNF为六角形基元的分形结构Fig.4.(a)Spin density isosurfaces on a basic hexagram David star representing up and down spins by blue and red colors respectively,the spin density is contoured at the value of 0.003/Å3and marked A and B indicating the different sublattices respectively where the net up spins reside;(b)the fractal structure with topology of David star as a basic hexagram.

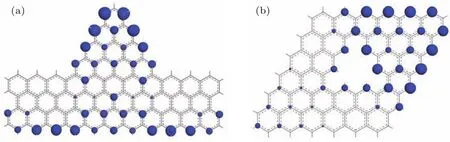
图5 (a)锯齿三角形GNF-GNR复合结构和(b)中间三角形镂空GNF的NBS电子自旋密度分布,自旋等密度面的密度值为0.04/Å3Fig.5.Representative(a)zigzag-edged triangular GNF connected with GNR and(b)GNF with internal zigzagedged triangular vacancy,rendering spintronic components illustrated with the spin density distribution projected from the NBS from first-principles calculation by the isosurface of spin density contoured at 0.04/Å3.

4 结 论

本文按照形图理论分析几种典型形状GNF的自旋特性,并采用全电子数值轨道基组方法进行第一性原理电子结构计算,证实了形图理论结构的正确性.根据锯齿边缘三角形GNF由拓扑挫折产生的净自旋随线性尺度增加,提出由石墨烯原子层平面刻蚀各种图案的GNF来获得大自旋和控制自旋态分布的基本设计原理,证明利用自旋磁特性与形状的关联性,通过雕琢有限石墨烯片段是实现自旋电子纳米器件的有效途径.