多属性逆向同步增价拍卖模型及最优投标策略

冉茂盛,黄 俊,蒋卫艳

(1.重庆大学经济与工商管理学院,重庆400030;2.香港理工大学建筑及房地产学系,中国香港999077)

1 引 言

逆向拍卖又被称为采购拍卖,是一种存在唯一卖方(采购商)和多个竞争性买方(供应商)的拍卖形式.随着互联网的普及和电子商务的发展,逆向拍卖机制已经被越来越广泛的用于企业的电子采购[1].由于采购商在进行电子采购时,除了关心物品的提供价格外,往往还会考虑物品的质量、交货期和售后服务等其他非价格属性,例如在飞机采购合同中,产品的质量、交货期等与价格处于同等重要的位置.多属性逆向拍卖日渐成为电子采购的主流形式,并成为拍卖理论研究的热点之一.

早期的文献主要研究单物品的多属性拍卖.Che[2]基于投标人成本独立的前提,提出了二维多属性拍卖模型,而Branco[3]则研究了基于投标人成本相互关联前提的二维多属性拍卖模型.在Che的研究基础上,David[4,5]进一步将模型扩展到任意多维属性的情形,构建了一般意义上的多属性拍卖模型.孙亚辉等[6]对David的模型进行改进,使其更符合现实且具有更广泛的适用性.曾宪科等[7]在模型中加入了质量属性最低值的约束,建立了基于非对称投标人的多属性英式逆向拍卖模型,并得出了供应商的均衡投标策略.此外,王明喜等[8]通过对采购商的评分函数进行修改,建立了基于简单加权法的多属性逆向拍卖模型,从而解决了价格属性和质量属性量纲不统一和数值不可比的难题.

而现实中的采购商往往一次性采购多个物品,且物件间又具有一定的互补性,此时单物品的多属性拍卖机制已不能满足实践的要求.于是,此后的研究将多属性拍卖从单物品情形拓展到多物品情形.在组合效应存在的前提下,关于多物品多属性拍卖的文献主要研究以下两种拍卖机制:1)同步二级价格密封拍卖(simultaneous sealed-bid second-price auction,SSA)机制.在Krishna等[9]包含两类供应商的单属性SSA拍卖模型的基础上,黄河等[10]将多属性拍卖引入SSA机制,建立了采用SSA机制的多物品多属性逆向拍卖模型,并分析了物品组合效应对供应商投标策略的影响.2)动态拍卖机制.在另一篇论文中,黄河等[11]基于组合拍卖规则,设计了一种多属性逆向拍卖的动态机制,并分析了投标者的均衡投标策略.姚升保[12]则在Zhang等[13]研究的基础上,将多轮逆向拍卖机制(iterative multi-attribute multi-unit reverse auction,IMMRA)引入到多属性拍卖中,研究了采购商信息披露政策对拍卖的影响.

上述关于多物品多属性拍卖的文献,均未涉及同步增价拍卖(simultaneous ascending auction,SAA)机制下的多属性拍卖.同步增价拍卖是单物品英式拍卖在多物品情形下的推广,该机制中的多个物品同时进行公开叫价,直到所有物品的出价均不变时拍卖结束,物品的最高出价人获得相应物品[14].SAA机制作为一种重要的多物品拍卖机制,由于可操作性强及便于投标者对标的物的比较选择,被各国政府大量应用于特定市场的牌照拍卖中,例如美国联邦通讯委员会(FCC)主要使用SAA机制来拍卖无线电频谱拍照[15].SAA机制还被用于采购拍卖中,现实中的采购商除关心物品的价格外,往往还会考虑物品的其他非价格属性,为了对该情形下的多物品拍卖进行分析,有必要研究多属性逆向SAA机制及其均衡策略.基于此,本文将同步增价拍卖机制引入到存在组合效应的多属性逆向拍卖中,建立了基于两类非对称供应商的多属性逆向同步增价拍卖模型.从供应商期望收益最大化角度,给出了两类非对称供应商的均衡投标(包括价格投标和非价格投标)策略,并验证了均衡最高得分关于组合效应单调递增.与黄河等[10,11]的密封多物品多属性拍卖机制不同,本文将一种应用最普遍的公开多物品拍卖机制—–SAA机制引入到多属性拍卖中去,从而进一步拓展了现有的多物品多属性拍卖理论[10-12].从机制设计的角度,一方面将Zheng[16]和Goeree等[17]的SAA机制由单属性拓展到了多属性,另一方面将黄河等[10]的多属性逆向拍卖由SSA机制拓展到了SAA机制.此外,由于SAA机制在现实中的广泛应用,研究作为其拓展的多属性逆向SAA机制,有利于指导现实的多物品多属性电子采购实践.

为此本文构建了多属性逆向同步增价拍卖模型,在推导出两类供应商的均衡非价格属性投标的基础上,得出了地方供应商的均衡价格投标策略,然后运用逆向递推法,进一步的分析给出了全局供应商的均衡价格投标策略,并对组合效应进行了比较静态分析.最后,通过在线拍卖的实例给出了两类供应商均衡投标策略的计算步骤及结果.

2 多属性逆向同步增价拍卖模型

多属性逆向同步增价(分)拍卖是多属性逆向英式拍卖由单物品向多物品的扩展.在多属性逆向同步增价拍卖中,采购商向多个潜在供应商采购n个物品,n个提供物品的竞拍同时进行.采购商对物品的要求包含价格属性和非价格属性,物品的分配由采购商制定的评分函数来决定.此时,供应商之间通过公开报分对提供物品的机会进行竞争,物品由获得最高得分的供应商提供,因此该拍卖又可以被称为多属性逆向同步增分拍卖.

本文考虑唯一的采购商采购两个物品.拍卖中有两类供应商,第一类供应商只对提供两个物品中的某一个有兴趣(有能力),称为地方供应商;第二类供应商对提供全部两个物品均有兴趣,且同时提供两个物品产生的价值大于分别提供这两个物品分别产生的价值之和,称为全局供应商.此时,同时提供两个物品给全局供应商带来的额外收益称为物品的组合效应,用α表示.

2.1 模型的基本假设

为简化分析,除假设物品的拍卖最小加分幅度无穷小之外,还建立了如下假设:

假设1采购商购买的物品具有1+m个属性,价格属性为p,其余m个相互独立的非价格属性用qj表示,j=1,2,...,m.模型中的非价格属性为为效益型属性,即属性值越大表明产品质量越高;而对于成本型属性,可运用取倒数或极差变换等方法转化为效益型属性.

假设2拍卖中的所有参与人都是风险中性的,且满足个体理性条件.因此,供应商选择在自身效用大于零时参加拍卖,且采供双方的效用均具有可加性.

假设3对任意非价格属性qj,采购商的效用递增,而边际效用递减;供应商的生产成本和边际生产成本均是递增的.

假设4供应商对所感兴趣物品的成本参数在区间上独立同分布,其分布函数及相应的密度函数分别为F(x)和f(x),是公共知识,且.特别的,由于地域的限制,地方供应商只能提供某一个物品;全局供应商可同时提供两物品,且对两物品的成本参数相同,这与Krishna等[9]的假设相同.

假设5拍卖中有两个地方供应商和一个全局供应商,全局供应商同时提供两个物品时获得的额外收益即为组合效应,用α表示,为正常数.这里从收益角度来理解组合效应,但若从成本角度看,组合效应可被视为成本的减少,即供应商提供两个物品可以享受规模经济.然而,无论是理解为收益的增加还是成本的减少,都不会对最终的分析产生影响.

假设6供应商的类型为共同知识,而组合效应及成本参数为相应供应商的私人信息,其他供应商只知道其分布函数.不同于Krishna等[9]和Albano等[18]关于α为公共知识的假设,这里更具一般性的假设α为全局供应商的私人信息.

2.2 采购商的效用函数与评分函数

在多属性拍卖中,采购商以价格p购买非价格属性值为q1,q2,...,qm的物品时,其获得的效用为

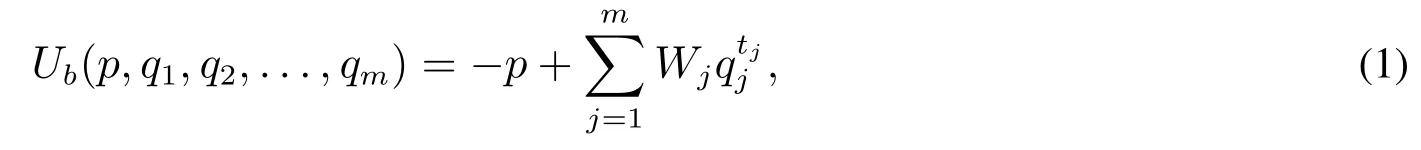
其中Wj为采购商赋予非价格属性qj的权重,表示其对qj的偏好程度,且Wj＞0;tj为采购商赋予非价格属性qj的幂次,则0＜tj＜1表示采购商边际效用关于qj递减,与假设3一致.Wj和tj为采购商的私人信息.

假设采购商对不同物品的Wj和tj相同.用pi表示采购商购买物品i的价格,则采购商购买两个物品时的效用为.

评分函数是由采购商制定并在拍卖前向所有潜在供应商公布的获胜者确定及物品分配方案,由价格属性p和非价格属性q1,q2,...,qm构造而成.采购商公布的评分函数可能偏离其真实效用,其评分函数为

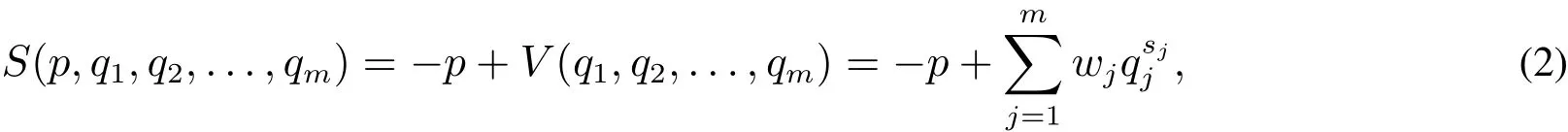
2.3 两类供应商的效用函数

若成本参数为θ的供应商以价格p及非价格属性值q1,q2,...,qm获得提供物品的机会,则其效用函数为

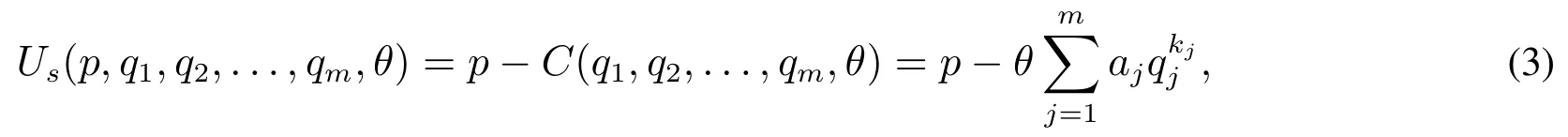
用pi表示全局供应商对物品i的价格属性投标,由于同时提供两个物品可获得额外收益α,故此时全局供应商获得的总效用为.

2.4 多属性逆向同步增价拍卖机制描述

首先,由采购商公布拍卖的规则,包括所拍卖物品包含的价格属性和非价格属性(质量)、物品数量、评分函数和结束规则等.

然后,是供应商竞分及获胜者确定阶段.以两个地方供应商和一个全局供应商的情形为例进行说明.两个物品的采购同时进行,两地方供应商分别参与相应物品的采购竞标,而全局供应商同时参与两个物品的采购竞标.采用公开叫分的方式,两类供应商根据评分函数计算出的得分进行竞争,直至两物品的采购中都仅剩唯一供应商时采购结束.仅剩的供应商获得提供对应物品的合同.

最后,每个物品的最终获胜者为相应拍卖中得分最高的供应商,获胜者按照其投标的价格属性值和非价格属性值配置出售物品.

3 两类供应商非价格属性均衡投标策略

在多属性逆向同步增价拍卖中,供应商的投标策略由价格属性值p和非价格属性值q1,q2,...,qm构成,供应商根据评分函数计算出的得分进行投标.不同于密封拍卖的一次性报价(分),本文的模型为公开拍卖形式,供应商通过互相竞分直至最高得分者胜出,此时供应商的均衡策略就意味着其最优退出水平.在给定采购商的评分函数和供应商效用函数的前提下,供应商的目标为选择合适的价格属性值p及非价格属性值q1,q2,...,qm,计算得出可接受的最高得分以最大化其期望效用.

在非价格属性的投标方面,全局供应商和地方供应商是对称,下面的定理给出了两类投标者的非价格属性投标策略.

定理1给定采购商的评分函数和供应商的效用函数,在第一得分拍卖中,供应商的最优非价格属性值q1∗,q2∗,...,qm∗独立于价格属性p和其他供应商的策略,为.进一步的,由一阶条件可以得到

证明运用反证法.给定供应商成本参数θ,假设存在至少一个非价格属性值使投标组合(p,q1,q2,...,qm)最大化供应商期望效用π(p,q1,q2,...,qm,θ).再构造一个投标策略组合(p′,q∗1,q∗2,...,q∗m),其中p′=p+V(q∗1,q∗2,...,q∗m)-V(q1,q2,...,qm),故S(p,q1,q2,...,qm)=S(p′,q∗1,q∗2,...,q∗m).此时,如果证得构造的策略组合(p′,q∗1,q∗2,...,q∗m)带给供应商的效用大于策略组合(p,q1,q2,...,qm)的效用,那么就与假设矛盾,从而原命题成立,即最优非价格属性qj=q∗j.

下面只需证策略组合(p′,q∗1,q∗2,...,q∗m)带给供应商的效用大于策略组合(p,q1,q2,...,qm).用G(S)表示供应商得分为S时获胜的概率.此时,供应商的期望效用为

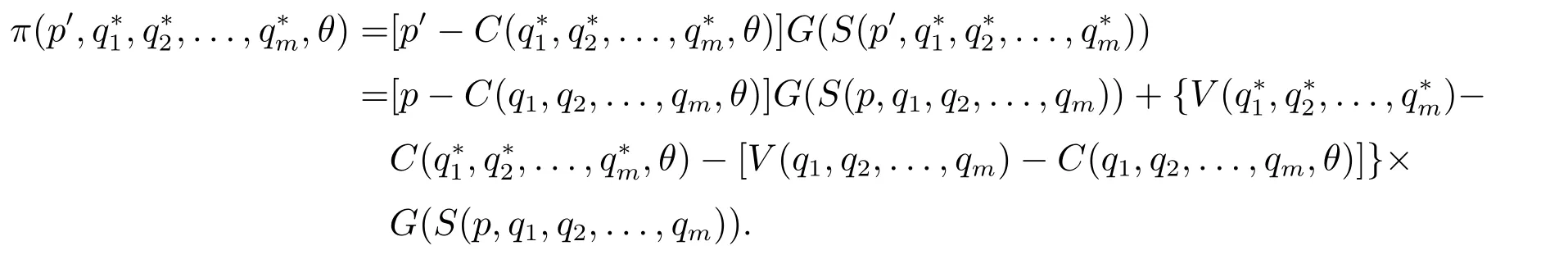
由q∗j(θ)的定义,可知V(q∗1,q∗2,...,q∗m)-C(q∗1,q∗2,...,q∗m,θ)＞V(q1,q2,...,qm)-C(q1,q2,...,qm,θ).于是,有

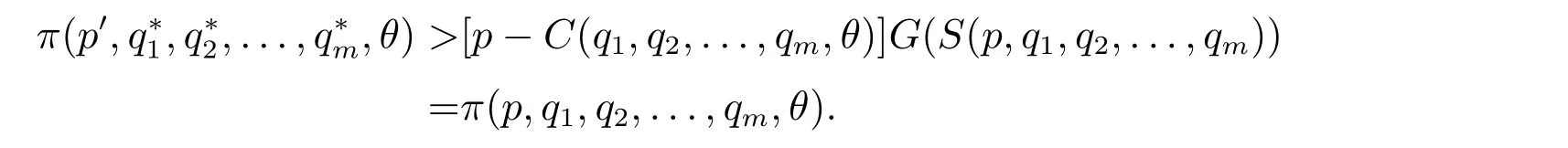
因此,原命题成立.再由一阶条件,可得式(4)成立. 证毕.

定理1的证明与Che[2]和曾宪科等[7]的方法类似.由定理可以看出,供应商的非价格属性投标在每轮投标中固定不变且不受组合效应影响.而由于全局供应商对两个物品成本参数相同,所以其非价格属性投标策略也相同.为进一步分析,给定由定理1所确定的非价格属性均衡策略,均衡时采购商估值函数可表示为V(θ)≡V(q∗1,q∗2,...,q∗m),供应商的成本函数和得分函数可分别表示为C(θ)≡C(q∗1,q∗2,...,q∗m,θ)和S(θ)≡S(p,q∗1,q∗2,...,q∗m).

4 两类供应商价格属性均衡投标策略

组合效应对全局供应商均衡投标策略的影响主要体现在价格属性投标方面,全局供应商和地方供应商在价格属性投标方面不再对称.在多属性逆向拍卖中,由于供应商的非价格属性投标均为固定不变的,供应商之间的竞争本质上是价格属性投标的竞争,故这里的价格属性均衡投标策略是指供应商的价格属性投标最低值.

4.1 地方供应商价格属性均衡投标

地方供应商的占优策略为在其效用等于零时退出,这是由于:对于使得效用为正的价格属性值,地方供应商是有利可图的,故其会继续参加投标;对于使得效用为负的价格属性值,理性的地方供应商不会选择参与拍卖,所以在效用等于零时退出,此时的均衡投标策略满足激励相容和个体理性条件.由于非价格属性投标固定不变,由此可以确定出其价格属性投标策略.于是,可以得到如下定理.

定理2给定采购商的评分函数和供应商的效用函数,在第一得分拍卖中,物品相应地方供应商的均衡价格属性值(最低出价水平)为

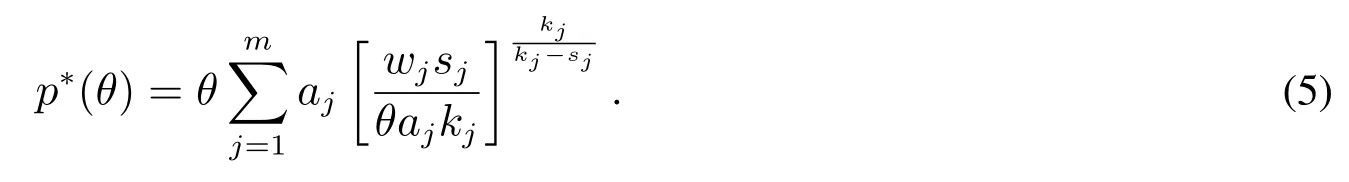
进一步地,地方供应商均衡投标的最高得分为

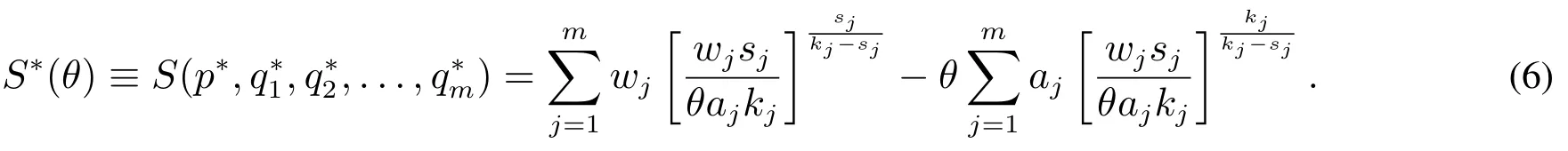
证明由于地方供应商在最低出价水平时的效用为零,即

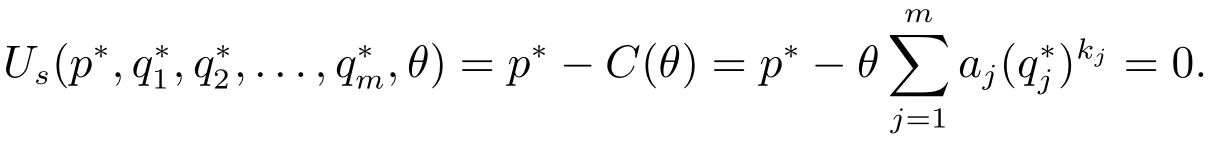
推论1在第一得分拍卖中,地方供应商的均衡价格属性值p∗(θ)和均衡投标的最高得分S∗(θ)关于成本参数θ严格单调递减.

证明在式(5)中,对θ求导,可得

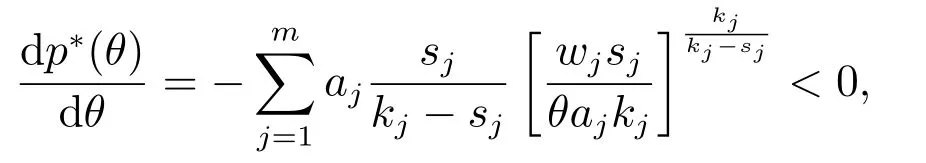
其中kj-sj＞0.所以,p∗(θ)关于成本参数θ严格单调递减.在式(6)中,对θ求导,可得

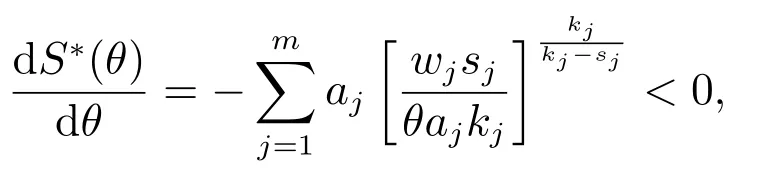
即S∗(θ)关于成本参数θ严格单调递减. 证毕.

由定理2可以看出,该机制中地方供应商价格属性投标策略与多属性逆向英式拍卖模型中的相同,最小加分幅度为D时,即为曾宪科等[7]得出的结论.此外,由地方供应商最高得分S∗(θ)=V(θ)-C(θ)及推论1,得V′(θ)-C′(θ)＜0.

4.2 全局供应商价格属性均衡投标

组合效应的存在使得全局供应商的价格属性投标策略复杂化,下面对此进行分析.由于供应商的最高得分决定了拍卖的结果,而由推论1可知成本参数与非价格属性均衡投标及地方供应商的最高得分一一对应,故可通过分析全局供应商均衡投标最高得分及对应水平的局部供应商成本参数来推出其价格属性均衡投标.

用S∗(1)(θ)和p∗(1)(θ)分别表示仅剩一个地方供应商(或物品)时私人成本为θ的全局供应商的均衡投标的最高得分和价格属性值;用S∗(2)(θ)和p∗(2)(θ)分别表示剩余两个地方供应商(或物品)时全局供应商的均衡投标的最高得分和价格属性值.用θ(1)表示以分数水平S∗(1)(θ)为均衡最高得分的地方供应商成本参数,有S∗(1)(θ)=S∗(θ(1));用θ(2)表示以分数水平S∗(2)(θ)为均衡最高得分的地方供应商成本参数,有S∗(2)(θ)=S∗(θ(2)).根据S∗(θ)关于θ递减,有θ(1)≡S∗-1(S∗(1)(θ))和θ(2)=S∗-1(S∗(2)(θ)).用θmin表示两个地方供应商中的较小私人成本,用θmax表示两个地方供应商中的较大私人成本.用Fn(θ|p)=[F(θ)/F(p)]n表示n个地方供应商中的最大私人成本小于水平p前提下,该最大私人成本小于θ的条件概率,n=1,2.

从决策顺序角度,全局供应商的竞拍决策分为两个阶段:在第一阶段,若S∗(2)(θ)＜S∗(θmax),则全局供应商在分数达到S∗(2)(θ)时退出拍卖;若S∗(2)(θ)≥S∗(θmax),则以分数S∗(θmax)获得提供该物品的机会并进入拍卖的第二阶段.在第二阶段,若S∗(1)(θ)＜S∗(θmin),则全局供应商在分数达到S∗(1)(θ)时退出拍卖;若S∗(1)(θ)≥S∗(θmin),则以分数S∗(θmin)获得提供该剩余物品的机会.

定理3给定采购商的评分函数和供应商的效用函数,假定φ(θ,θ(2))关于θ(2)在[θ,θ]内为凸函数,在第一得分拍卖中,该逆向拍卖机制存在一个精炼贝叶斯均衡.全局供应商第一阶段的均衡投标最高得分S∗(2)(θ)=S∗(θ∗(2)),相应的均衡价格属性投标p∗(2)(θ)=V(θ)-S∗(2)(θ).其中,

而θ(+2)为方程的唯一根或两根中的较大者;全局供应商第二阶段均衡投标最高得分S∗(1)(θ)=S∗(θ∗(1)),相应的均衡价格属性投标p∗(1)(θ)=V(θ)-S∗(1)(θ).其中

而θ+(1)为方程S∗(θ(1))=V(θ)-C(θ)+α的唯一根.

证明运用逆向递推法,先看第二阶段全局投标人的均衡策略.此时,全局供应商已经是第一件物品的获胜者.成本参数为θ的全局供应商在S∗(1)时退出,其对S∗(1)(θ)选择可转化为选择θ(1)以最大化期望收益

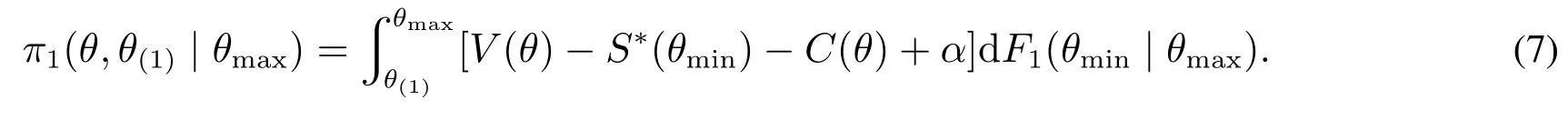
上式对θ(1)求偏导数,得到以下一阶条件

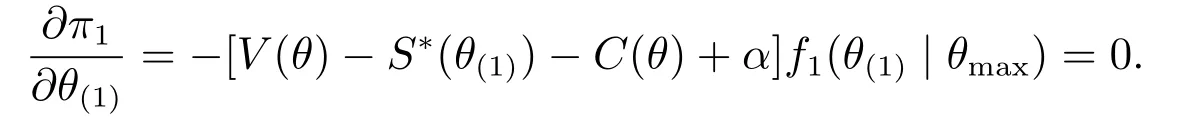
当S∗(θ(1))=V(θ)-C(θ)+α时,π1(θ,θ(1)|θmax)取到最大值,用θ+(1)表示方程的解.由于

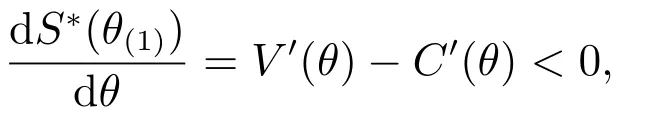
故方程的解θ(+1)唯一.由S∗(θ(1))的单调性及,存在唯一使得成立.此时,对所有,全局供应商选择最大化其期望收益;对所有,选择最大化其期望收益.于是,由θ∗(1)可得全局供应商的均衡投标最高得分.再由评分函数式(2),可得全局供应商在第二阶段的均衡价格属性投标.

再看第一阶段全局投标人的均衡策略.第一阶段全局供应商同时参加两件物品竞拍.在地方供应商私人成本均小于p前提下,全局供应商在S∗(2)(θ)时退出拍卖,其对S∗(2)选择可转化为对θ(2)选择以最大化期望收益

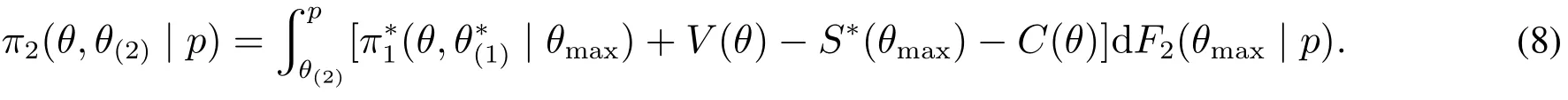
上式对θ(2)求偏导数,得到以下一阶条件

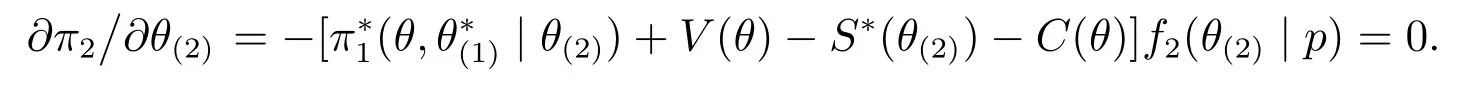
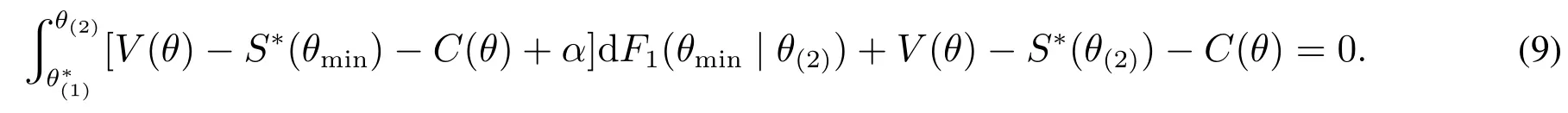
由φ(θ,θ(2))关于θ(2)的凹凸性,可知方程φ(θ,θ(2))=0最多存在两个根,用表示方程的唯一根,或者两根中的较大者.如果方程存在唯一的根,则为局部最优点;如果方程存在两个根,由凸性假设可知为凹函数,而的导数在方程的较大根处取值为负,此时也是局部最优点.为得到全局最优解,再比较边界解和内解.本文采用类似于Krishna等[9]和黄河等[10]的方法,定义.由于

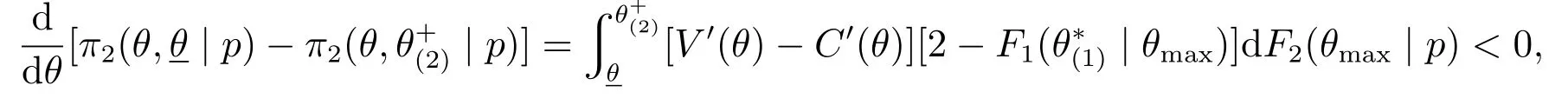
从定理3的结论中可以观察到:首先,均衡价格属性投标p∗(1)独立于全局投标人在第一阶段的投标策略,而只取决于其成本系数和组合效应;其次,p∗(2)不但取决于其成本系数和组合效应,还与私人成本系数θmin的分布有关;最后,私人成本系数θmax不影响全局投标人的均衡价格属性投标p∗(1)和p∗(2),但是只有当时拍卖才会进入第二阶段.

推论2给定采购商的评分函数和供应商的效用函数,对所有可得

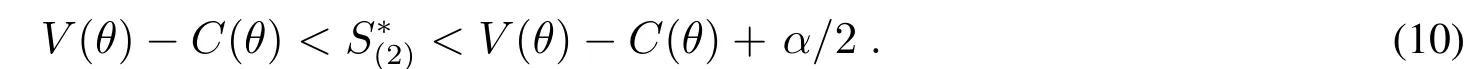
证明对,由式(9),有

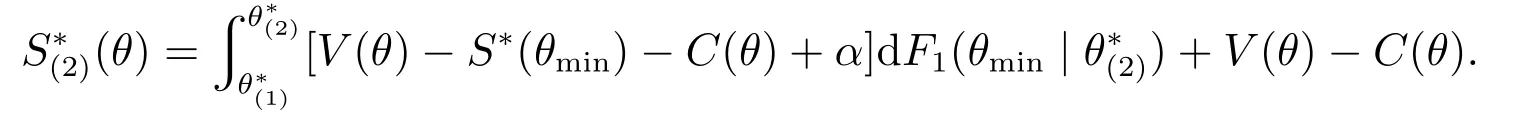
另一方面,由于

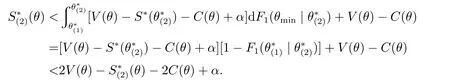
所以S∗(2)＜V(θ)-C(θ)+α/2. 证毕.

4.3 两类供应商投标策略的比较静态分析

以上部分均基于给定的α来分析两类供应商的投标策略,下面分析α变化时供应商均衡策略变化情况.

对于地方供应商,由定理2可知,组合效应α对其均衡策略没有影响.而对于全局供应商,由定理3可知,全局供应商在第一阶段和第二阶段的均衡投标策略均受α影响.于是,下面定理分析了组合效应对全局投标人均衡策略的影响.

定理4给定采购商的评分函数和供应商的效用函数,在第一得分拍卖中,全局供应商在两阶段的均衡投标最高得分S∗(1)(θ)和S∗(2)(θ)关于组合效应α单调递增,均衡投标价格属性值p∗(1)(θ)和p∗(2)(θ)关于组合效应α单调递减.

证明由定理3,对于第二阶段,在上,有,显然其关于α递增;而在上,为常数,由于,所以当α增大时,随之增大.也就是说,随着α增大,在上的关于α递增,同时随之增大,此时会使更大区域内的均衡投标最高得分为常数.同理,由,可以证得随α递减.

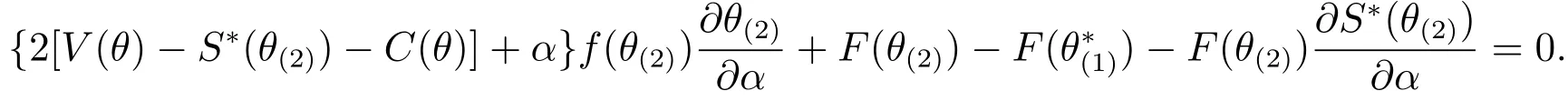
利用链式法则,上式可整理为

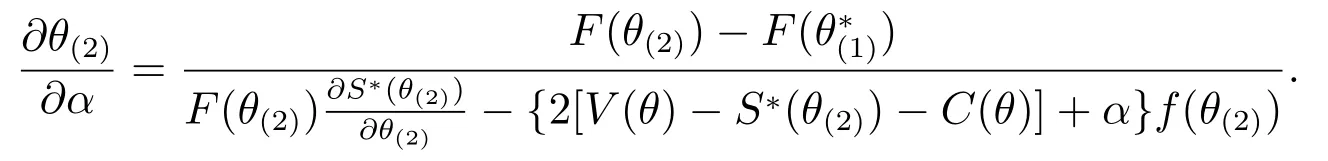
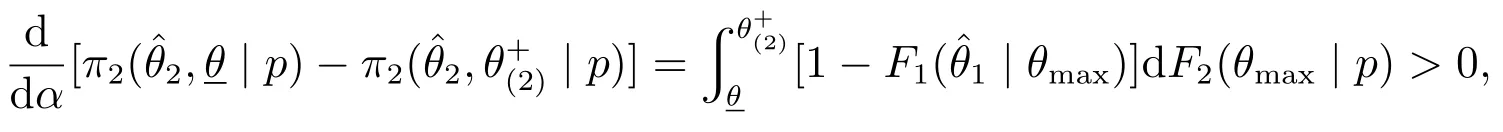
5 拍卖案例分析

假定某采购商通过逆向多属性同步增价拍卖机制在两相邻地域采购两件物品,该拍卖通过在线拍卖系统进行.地方供应商只需在系统中输入其成本参数,而全局供应商在系统中输入其成本参数和组合效应值,均衡投标的属性值由相应命题推导出的公式计算得出,此时投标人可利用在线拍卖系统的代理投标功能进行自动投标,并由该系统决定最终物品的分配和支付.

在该拍卖机制中,除所采购物品的价格属性外,采购商还关心物品所对应的两个非价格属性q1和q2.假定采购商公布的评分函数的参量w1=1,w2=2,s1=s2=0.5与其效用函数中的参量一致.拍卖中有两个地方供应商和一个全局供应商,其成本函数中的参量为a1=0.5,a2=0.25,k1=k2=1.5,两类供应商的成本参数在区间[0.2,0.6]上服从均匀分布.此时,.容易验证,函数φ(θ,θ(2))满足凸性要求.

对于给定的θ,根据定理1可以计算出两类供应商的均衡非价格属性值q∗1和q∗2;根据定理2可以计算出地方供应商的均衡价格属性值p∗和最高退出得分S∗.分别给定θ为0.2,0.3,0.4,0.5,0.6,局部供应商的均衡非价格属性值、最低价格属性值和最高得分的计算结果如表1所示.

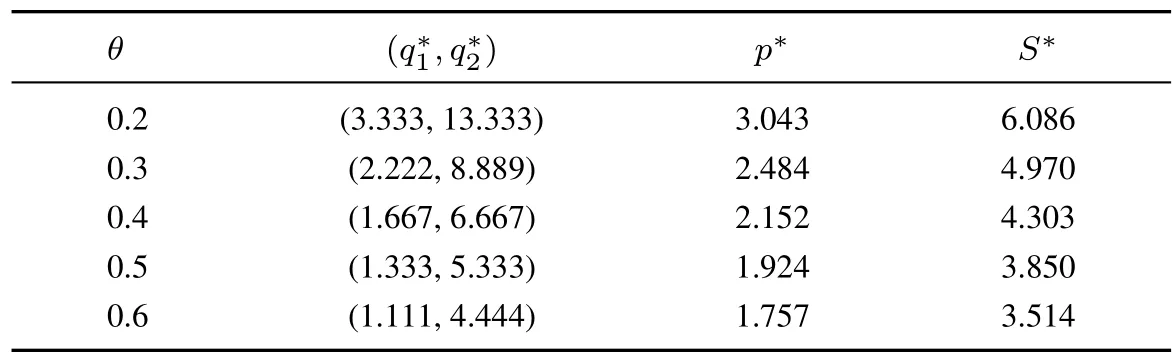
表1 地方供应商的均衡投标策略及最高退出得分Table 1 The local bidders’equilibrium bidding strategies and optimal drop–out scores

再给定α的取值,根据定理3可以计算出全局供应商在两阶段的均衡价格属性值以及相应的最高退出得分.具体的计算步骤如下:

步骤1根据确定分界点;

步骤2在上,有,根据,计算出.在上,根据计算出S∗(1)(θ)并求出唯一的根θ(+1),确定;

步骤3根据计算出的S∗(1)(θ),由p∗(1)(θ)=V(θ)-S∗(1)(θ)计算出p∗(1)(θ);

步骤4再计算拍卖第一阶段的内解.已知θ∗(1)及由供应商分布函数得到的条件分布函数,根据式(9)计算出θ(+2)为方程的唯一根或者两根中的较大者.再将不同θ所对应的期望收益π2(θ,θ(+2)|p)与边界点处的期望收益比较,从而确定出分界点;

步骤5在上,确定,在上,确定,从而计算出S∗(2)(θ),然后再由p∗(2)(θ)=V(θ)-S∗(2)(θ)计算出p∗(2)(θ).

下面的表2和表3给出了当α分别为0.5和1.0时,θ为0.2,0.3,0.4,0.5,0.6时,全局供应商在两阶段的均衡非价格属性值、最低价格属性值和最高得分的计算结果.

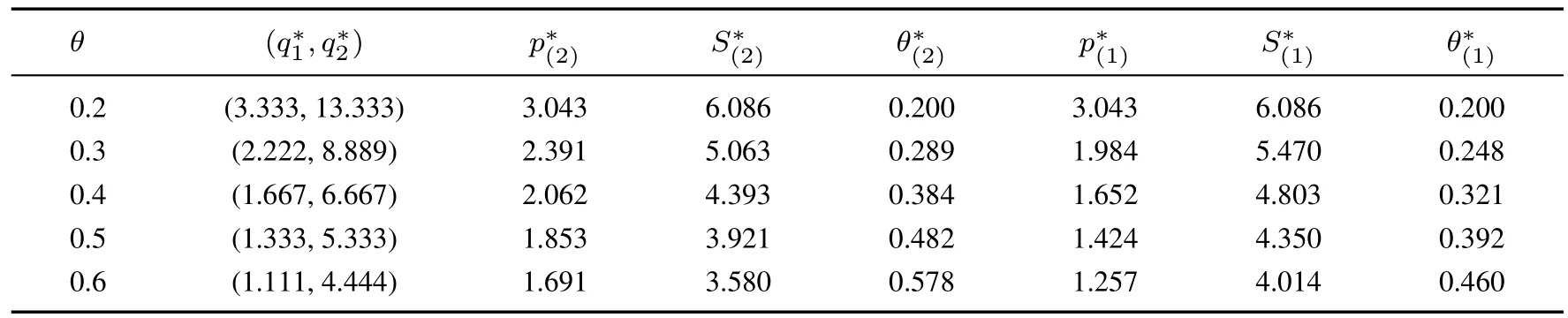
表2 当α=0.5时全局供应商的均衡投标策略及最高退出得分Table 2 The global bidder’s equilibrium bidding strategy and optimal drop-out score when α equals 0.5

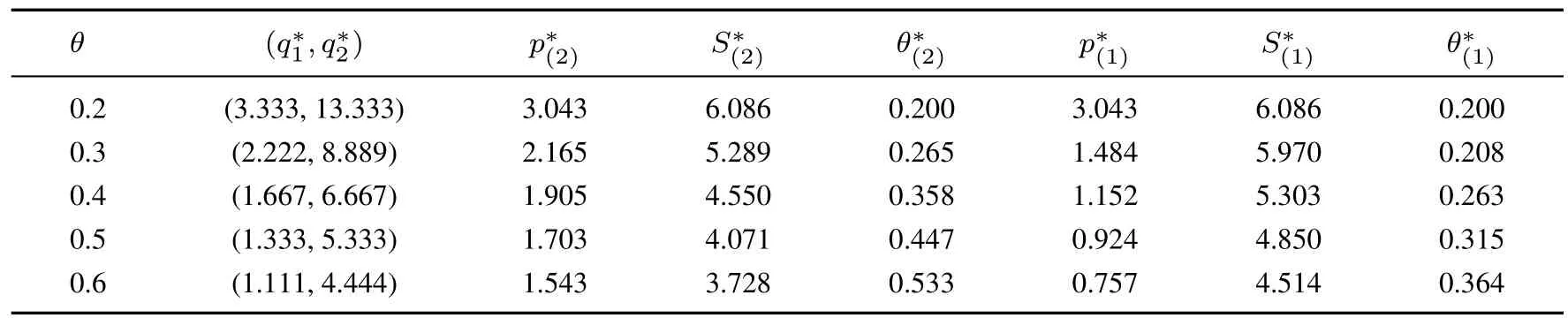
表3 当α=1.0时全局供应商的均衡投标策略及最高退出得分Table 3 The global bidder’s equilibrium bidding strategy and optimal drop-out score when α equals 1.0

比较表2和表3中的数据,可以看出:组合效应α越大,全局供应商在两阶段的均衡投标最高得分和越大,而最低投标价格属性值p∗.(1)和p∗(2)越小,这些结果与文中的定理相符.

下面以α=0.5情形为例进行说明.假定全局供应商的成本参数θ=0.5,两个地方供应商成本参数0.2≤θmin≤θmax≤0.6,查表可知:当θmax＜0.482时,全局供应商退出拍卖,两个地方供应商赢得拍卖且支付分数均为S∗(0.482)=3.921;当θmax≥0.482时,全局供应商赢得提供一个物品的机会,其支付分数为S∗(θmax),并进入拍卖第二阶段.在第二阶段,当θmin＜0.392时,全局供应商退出对第二个物品的竞拍,该阶段地方供应商的支付分数为S∗(0.392)=4.350;当θmin≥0.392时,全局供应商继续赢得提供第二个物品的机会,其支付分数为S∗(θmin),此时全局供应商获得了提供两个物品的机会.

6 结束语

在多属性拍卖中,多物品采购拍卖的相关研究尚不充分.基于存在两类非对称供应商的前提,本文将同步增价拍卖(SAA)引入多属性逆向拍卖中,设计了一种多物品多属性逆向拍卖机制,即多属性逆向同步增价拍卖机制.从供应商的角度出发,在研究了两类供应商的非价格属性均衡投标策略的基础上,分别对两类供应商的价格属性投标策略进行分析.针对公开竞分的拍卖形式和拍卖中存在的组合效应,将全局供应商的投标决策分为两个阶段进行研究,得出了该拍卖机制下的精炼贝叶斯均衡,并对影响策略的组合效应作了比较静态分析.最后,通过拍卖实例给出了两类供应商均衡投标策略的计算步骤,并对物品的分配和支付作了示例,以便于该机制在现实采购拍卖中的运用.

本文的分析只是基于两个物品的情形,运用类似的逆向递推法,容易分析采购物品多于两个的多属性逆向同步增价拍卖模型.另外,本文的分析主要基于供应商视角,未来的研究可以从采购商的角度进行分析,研究采购商所采取的最优评分规则及对拍卖结果的影响[21].