基于有限理性的需求模型与承诺交付时间研究

李海南,邱晗光

(重庆工商大学商务策划学院,电子商务及供应链系统重庆市重点实验室,重庆400067)

1 引 言

在现代商务尤其是电子商务环境下,在企业与顾客达成交易后,非即时的交付服务或长时间的交付过程通常因为可能出现的不可控因素表现出不确定性.这种不确定性可能导致顾客无法准确估计收货前的等待时间,企业也无法确定合理的服务价格、交付时间等,从而为双方带来不利的结果.在传统的管理实践中,解决这类问题可以采用忽视不确定性或利用历史数据进行预测的方法,但是这些做法会导致过于理想化的方案.而且,这种基于完全理性的做法也受到了来自心理学或行为经济学的极大挑战.还有一种方法就是把不确定因素处理成一种噪声,并把噪声看成是有限理性的结果,再对噪声进行估计.该方法也许不能圆满解决上述问题,但从某种意义上,至少比前一种方法更贴近实际.在考虑人的有限理性的行为运作研究领域,有学者从企业利润或社会福利最大化的角度研究服务系统的定价决策以及顾客有限理性的影响[1],本文研究这种情况下的承诺交付时间(promised delivery time,PDT)决策以及顾客有限理性的影响.

考虑一个提供交付服务的能力无限的企业.假定排队系统中的顾客无法准确估计逗留时间(包括等待时间和交付时间).首先,构造基于时间竞争的有限理性需求函数.其中,顾客采用随机选择规则,并根据企业的承诺交付时间和交付可靠性决定是否接受服务.其次,研究顾客有限理性对企业PDT决策的影响.结果表明,在顾客存在有限理性的情况下,企业的最优PDT存在并且随着顾客有限理性水平的增加而递减,而已有研究中基于完全理性的相关结论是本文的一种特殊情况.

在运作管理(OM)领域,与本文直接相关的研究包括有限理性建模和承诺交付时间(PDT)决策.排队系统的“平均到达率”在下列PDT决策类文献中被称为“需求率”,相应的需求率函数有时也称为需求函数.本文沿用需求率的称谓,在不引起混淆的情况下需求率函数也称为需求函数.

自文献[2]及文献[3]发表以来,行为运作管理成为研究的热点.在OM领域,有限理性建模的研究成果尚不丰富.

Su[4]假定在供应链环境下的报童没有准确选择订货量的能力,分析了几种常见分布的有限理性报童的订货量决策,发现把决策噪声和优化误差合并起来研究能得到与实验研究一致的结果.Ho等[5]讨论在由单制造商与单零售商组成的供应链中,假定零售商不能准确选择适当价格组合的情况下,完全理性制造商提供给零售商的两步收费定价合同的设计问题.Chen等[6]讨论在由单供应商、双零售商组成的供应链中,假定其中一个零售商无法理性地判断另一零售商策略的情况下,完全理性供应商的能力在零售商之间的分配博弈均衡.以上文献研究产品供应链中的不同问题,都把有限理性解释为决策噪声,采用Logit选择规则[7,8],得到的均衡结果均受到有限理性程度的影响.这样处理的一个必然结果就是,这些研究中基于完全理性的结论是基于有限理性的结论的一种特殊情况.与上述研究一样,本文假定顾客是有限理性的,但研究服务系统中的问题.

Huang等[1]研究服务系统中的有限理性,假定顾客在选择是否加入一个队列时缺乏准确估计预期等待时间的能力,把对等待时间的估计误差看成是噪声,影响顾客选择的因素是服务价格和预期逗留时间.在队列是否可视、是否采用最优价格的不同组合情况下,有限理性对以利润最大化为目标的企业和社会福利的影响是有差别的.与产品供应链研究不同的是,Huang等[1]在讨论顾客选择加入还是退出一个队列时,假定顾客等待时间的误差项服从Logistic分布[9,10],得到纯策略;而且顾客的有限理性水平被具体定义为单位时间的等待成本与等待时间误差项分布参数的乘积.Veeraraghavan等[11]研究排队系统中顾客在两个队列中选择加入其中一个时的从众行为,假定在选择前顾客不具有关于服务台的服务价值和队长的完全信息.采用贝叶斯规则,结果表明分别以效用最大和后悔值最小为目标的顾客表现出不同的程度的从众行为.

本文采用与Huang等[1]类似的需求函数建模方法,从时间竞争角度研究顾客的有限理性,影响需求率的因素是交付时间和交付可靠性;这与Huang等[1]从价格竞争角度的研究是不同的.有限理性建模除了上面的方法外,近期还出现了基于稀疏集[12]和通过人眼跟踪测量偏好的建模方法[13].其中,基于稀疏集的方法可以写成约束优化的形式.这似乎为利用传统优化理论研究行为运作问题提供了可能.

在考虑顾客行为的基于完全理性的研究中,于等[14]和朱等[15]在研究呼叫中心的运作问题时,考虑已知的提示等待时间对顾客行为的影响,引入顾客的等待耐心度参数从顾客离队概率角度建模.这类研究考虑的顾客行为不是有限理性的,但提供了另一种有限理性建模的思路.

关于PDT决策的研究,因为缺少从有限理性角度的研究,下面的文献都是基于完全理性假定的.假定顾客根据PDT或者包含PDT在内的因素组合决定是否接受服务.企业为达到最大利润,需要选择PDT或者联合选择包含PDT在内的策略组合.

So等[16]假定需求是产品价格和交付时间的函数,交付可靠性是内生变量,在行业存在交付可靠性门槛的情况下建立约束优化模型,得到关于定价、交付时间保证和能力扩张在内的决策方案.Boyaci等[17]假定需求对产品价格和交付时间敏感,讨论产品差异化与运作能力成本的相互影响,研究表明不同产品的绝对或相对的边际能力成本在形成企业的最优产品定位决策中起关键作用.Boyaci等[18]在Boyaci等[17]的研究基础上增加交付可靠性对需求的影响,对产品差异化与能力的相互影响进行了更深入的研究.Liu等[19]假定顾客对产品价格和提前期敏感,在由单个供应商和单个零售商组成的供应链中,二者进行Stackelberg博弈的情况下分权式供应链将导致源于市场和运作因素的无效率.这些文献讨论生产系统的PDT决策,采用线性的,或者可转化为对数线性的需求函数.

Shang等[20]研究排队系统的PDT和能力博弈,假定M/M/1排队系统的需求率受交付时间、交付可靠性的影响,服务价格是外生的.在研究PDT决策的过程中采用受交付可靠性的行业门槛约束的寡头博弈模型,得到唯一的Nash均衡.Xiao等[21]假定M/M/1排队系统的需求率是价格、交付时间、交付可靠性的函数,研究在交付时间、交付可靠性、制造商能力等是否内生以及生产成本是否为私人信息的不同组合情况下的供应链协调问题.与So等[16]一致,本文中的交付可靠性也是内生的.与本文研究形成直接对比的是Shang等[20]关于PDT竞争的研究.他们的需求模型虽然也考虑顾客选择行为,但这种选择是基于效用最大化的选择,与本文基于顾客满意的选择规则并不相同.

2 有限理性需求模型

2.1 基于完全理性假定的需求模型及其局限

取M/M/1的等待制排队系统,先到先服务.假定服务机构即企业以不变的服务价格和成本按订单交付（delivery to order,DTO）一种已经达成交易的产品.讨论被大多数基于时间竞争的文献采用的需求率函数,即受承诺交付时间L,交付可靠性α影响的单位时间需求λ,即

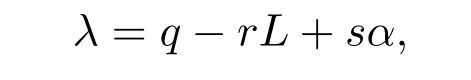
其中λ表示基于完全理性假定的单位时间内的需求率(简记为“完全理性需求率”);交付可靠性α被定义为顾客接受完交付服务时的逗留时间w的概率,即α=Pr(w≤L)=1-e-L(µ-λ),顾客逗留时间w是包含排队等待时间和服务时间的随机变量,µ表示企业的服务率;q,r,s均为非负常数,分别表示需求的固定部分、交付时间敏感性因子、交付可靠性敏感性因子.

由于交付可靠性是交付时间的函数,所以,在短期内企业的服务能力不变的情况下,这种基于完全理性假定的需求率函数是由交付时间决定的,企业可以通过选择适当的承诺交付时间来影响需求.然而,实际交付过程具有不确定性,顾客往往无法准确估计逗留时间.在交付过程中一旦发生不可预期的突发事件,顾客的实际等待或服务时间可能比承诺交付时间更长.这说明,基于完全理性的传统需求率函数并没有考虑顾客有限理性的影响,不适用于有限理性的情况.因此,需要对其修正或者建立有限理性需求函数.

2.2 有限理性需求函数

假定顾客无法准确估计逗留时间,但是可以根据历史数据拟合逗留时间的分布,尤其对于有重复购买经历的顾客大抵如此.假定顾客对逗留时间的估计误差项ε服从参数为θ的Logistic分布,其分布函数F(x)=1/(1+e-x/θ),其中0＜θ＜1.在服务完成后顾客获得的预期效用U=R-CEw,其中R表示逗留时间为0时顾客从产品和服务中获得的净效用,已经从R中剔除了产品和服务的价格；C表示顾客的单位时间逗留成本;Ew表示顾客的预期逗留时间.如果有限理性顾客加入队列的条件是R-C(Ew+ε)≥0,即U≥Cε,那么,根据随机选择规则[7],有限理性顾客接受交付服务的概率就是φ=F(U/C).这里“加入队列”意味着顾客下订单并接受服务.概率φ表示净期望效用非负的选择概率,反映顾客在效用方面的要求.与Huang等[1]一致,取顾客的有限理性水平β=Cθ.下文将用β/θ替换C.对于完全理性顾客有β=0.

关于顾客的预期逗留时间与承诺交付时间的关系,由于λ=q-rL+sα,一方面,企业承诺比顾客预期逗留时间更短的交付时间可以提高对时间敏感的顾客的需求量,从而Ew≥L；另一方面,由于交付可靠性是交付时间的增函数,所以企业也可以承诺比预期逗留时间更长的交付时间来提高对交付可靠性敏感的顾客的需求量,从而Ew≤L.不失一般性,这里取Ew=L,则U=R-Lβ/θ.因此,顾客接受交付服务的概率φ=F(θR/β-L)=1/(1+e-(R/β-L/θ)),且在L上是递减的.当β由0变化到+∞时,φ由1变化到1/(1+eL/θ);且在L=0 时,1/(1+eL/θ)等于1/2.

因为概率φ包含了顾客的有限理性因素,那么就可以用φ对完全理性需求率函数进行修正.考虑到φ的值域属性,应用乘法规则得到下面的有限理性需求率函数Λ,即

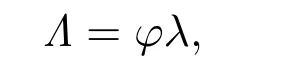
其中φ=1/(1+e-(R/β-L/θ)),λ=q-rL+sα,α=1-e-L(µ-λ),且R,µ,q,r,s,θ,β是非负常数,0＜θ＜1.

有限理性需求率函数除了包含承诺交付时间、交付可靠性外,还包含顾客的效用条件,其中的有限理性水平参数把顾客的理性程度由极端的完全理性扩充到一个变化范围,可以适用于不同理性程度的顾客,比传统的需求模型更具有普适性.对有限理性需求率函数进行简单推导可以得出下列结论.

定理1有限理性需求率在顾客有限理性水平上是递减的；而且

1)当顾客的有限理性水平趋于0即处于完全理性时,有限理性需求率逼近完全理性需求率λ；

2)当顾客的有限理性水平趋于正无穷大时,有限理性需求率达到最小值λ/(1+eL/θ).

定理1的证明略.

3 PDT决策

3.1 基于有限理性需求的利润最大化问题

假定企业在短期内DTO服务的价格不变、有充分大的不变的服务能力µ(≥λ),以承诺交付时间L作为决策变量,此时交付可靠性α是内生的.不失一般性,假定q≤µ.在有限理性需求率函数中,把α=1-e-L(µ-λ)代入λ=q-rL+sα得到λ=q-rL+s(1-e-L(µ-λ)),即λ+se-L(µ-λ)+rL=q+s.在参数s,µ,r,q给定的情况下,用λ=λ(L)表示由方程λ+se-L(µ-λ)+rL=q+s确定的隐函数.在服务的价格和成本均不变的情况下,利润最大化等价于需求率最大化.结合前面的分析可以得到下面的问题

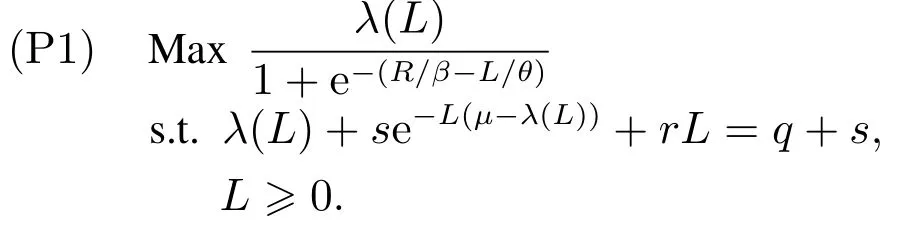
3.2 对于完全理性的情况

取β=0,则φ=1,这是顾客完全理性的情况.问题(P1)化为完全理性需求率最大化问题,即

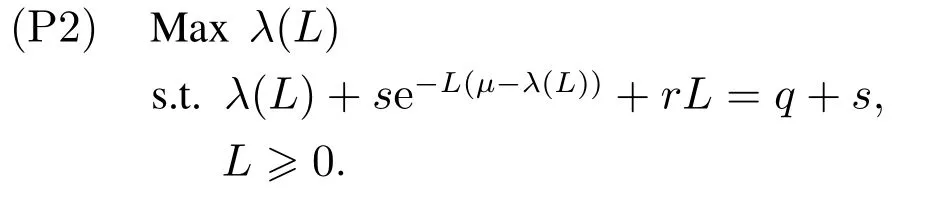
定理2对于问题(P2),在顾客的有限理性水平等于0即完全理性的情况下,当µ-λ(L)＞r/s时,企业的最优承诺交付时间由最优方程(µ-λ(L))se-L(µ-λ(L))-r=0确定;否则,最优承诺交付时间为0.

证明见附录.

在定理2中,如果用L∗、λ∗分别表示最优PDT以及最优PDT下的需求率;那么,当µ-λ∗＞r/s时,通过最优PDT方程可得到唯一的.因此,定理2的结论与Shang等[20]中的多个企业的PDT竞争的Nash均衡结果一致(注意模型不考虑交付可靠性的行业门槛,对应于Shang等[20]γ取0的情况).

3.3 对于有限理性的情况

取β＞0,问题(P1)是有限理性需求率最大化问题.

定理3对于问题(P1),在顾客的有限理性水平大于0即非完全理性的情况下,企业的最优承诺交付时间存在,并且最优PDT由方程确定.

证明见附录.

定理3中的最优PDT方程无法求得显式解;在给定参数的情况下,可以借助计算软件求得数值解.

4 数值算例分析

4.1 有限理性需求率的变化情况

取µ=25,q=15,r=1,s=1,R=90,θ=0.5,而β选取若干不同的值,对有限理性需求率函数作图并分析曲线的变化情况(如图1).

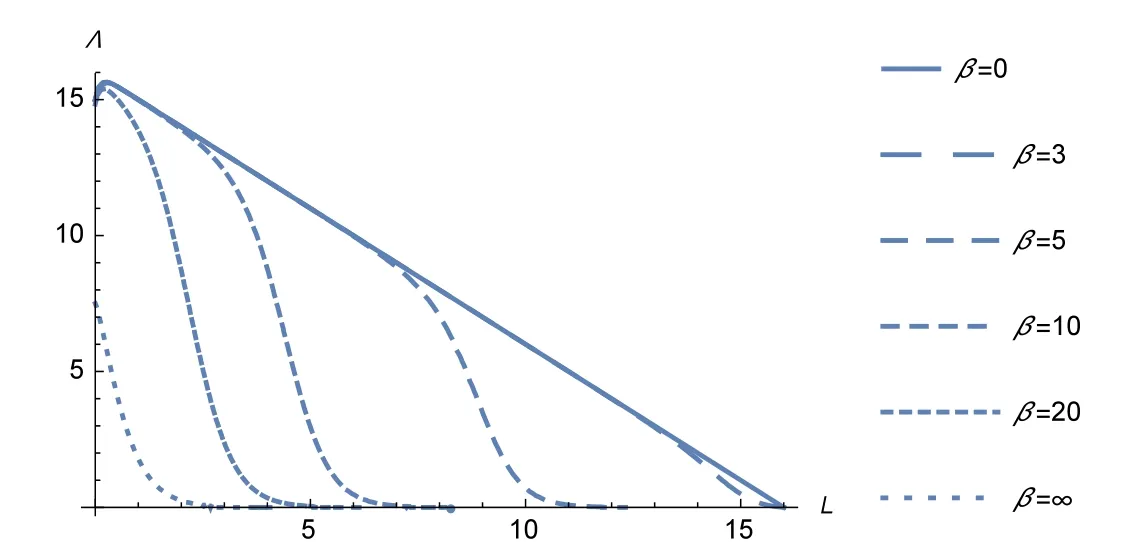
图1 不同有限理性水平下的需求率曲线Fig.1 Demand rate curves with various BR levels

定理1是有限理性需求率曲线的两种极端情况,分别对应于图1的左下方和右上方的边线.当L=0时,有限理性水平β趋于∞时的需求量是在完全理性时需求量的一半,即φ达到1/2.由图1可以看出,除了β趋于∞这种极端情况外,随着L的逐渐增加,有限理性需求率开始是递增的;当到达一个最高点后,有限理性需求率是递减的.一个合理的解释是,开始的需求率增加是由于PDT延长引起的交付可靠性增加带来的需求率增加占优势,即开始的PDT延长表现出正效应；随着PDT的进一步延长,交付可靠性的增加效应有限而PDT延长的负效应占优势,因此需求率下降.有限理性水平越高,在相同的交付时间下,需求下降得越多.

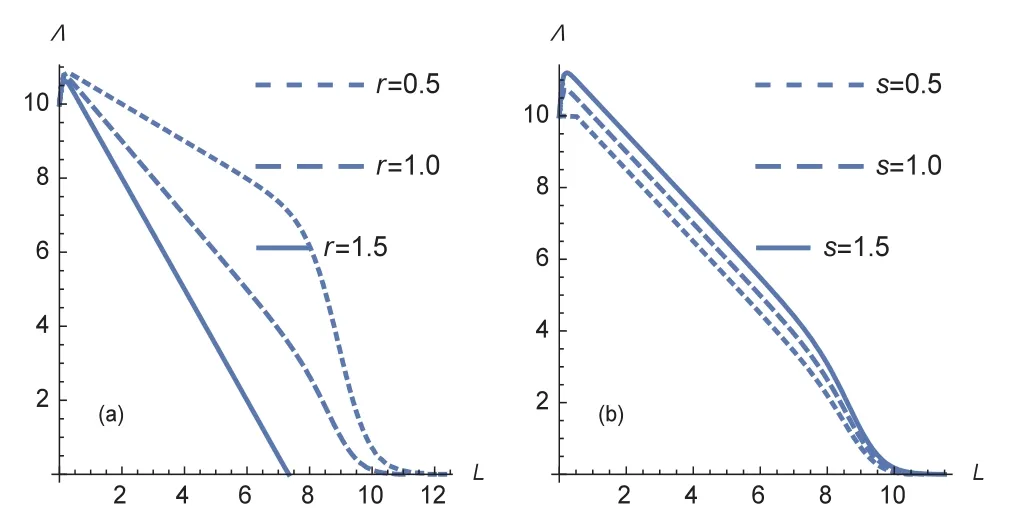
图2 β＝5时的有限理性需求率变化((a)中s=1,(b)中r=1)Fig.2 BR demand curves withβ＝5(s=1 in(a),and r=1 in(b))

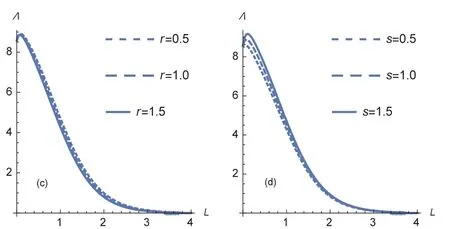
图3 β＝50时的有限理性需求率变化((c)中s=1,(d)中r=1)Fig.3 BR demand curves with β＝50(s=1 in(c),and r=1 in(d))

下面通过数值例子观察,当交付时间因子、交付可靠性因子分别取不同值时的有限理性需求率的变化情况.取µ=20,q=10,R=90,θ=0.5,图2和图3是β分别取5和50的情况.在时间因子变化的图2(a)和图3(c)中s=1,在交付可靠性因子变化的图2(b)和图3(d)中r=1.相较于交付可靠性因子,在有限理性水平较低时交付时间因子的变化对有限理性需求率的影响似乎更为明显(如图2(a));在顾客有限理性水平较高的情况下,两个因子的变化对有限理性需求率的影响都不明显(如图3).考虑到效用条件U=R-L·β/θ≥0,在本例中只有β≤45/L的顾客才会进入排队系统.可以认为,有限理性水平越高的顾客对交付时间的要求会越短.这说明,PDT决策对有限理性水平偏低的顾客最有效.

4.2 最优承诺交付时间及其与有限理性水平的关系

对于定理3中的最优PDT方程,由于λ=λ(L)是由λ-(q-rL+s(1-e-L(µ-λ)))=0确定的隐函数,所以最优PDT是下面方程组的解,即

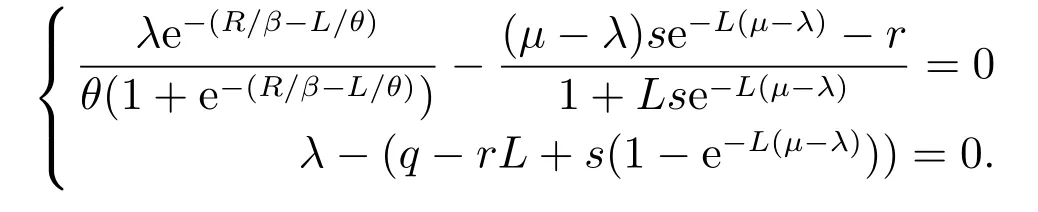
取µ=25,q=15,r=1,s=1,R=90,θ=0.5,β=1,得到唯一的最优解L∗=0.24.为显示曲线的变化趋势,通过图示解以便于观察解的情况(如图4).顺次改变参数β,其它参数保持与图4一样,求出相应的L∗就能得到最优PDT的变化趋势图(如图5).

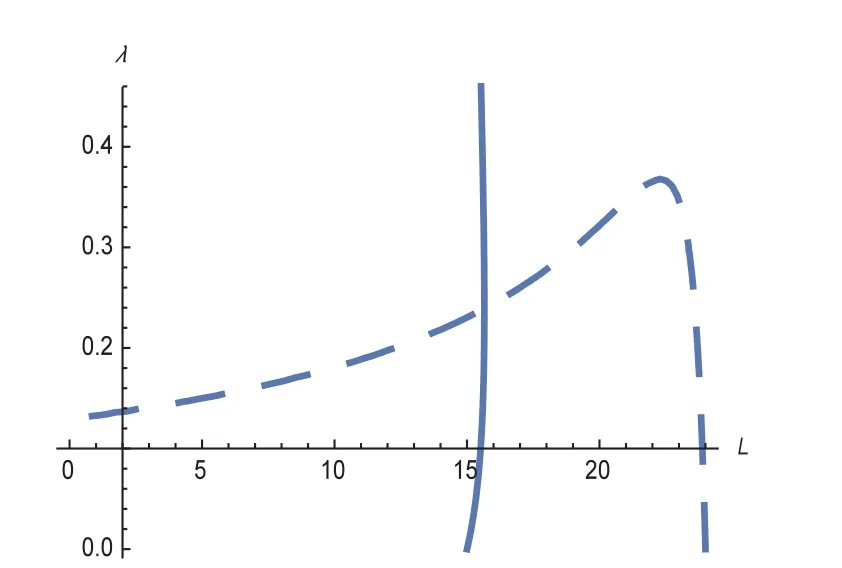
图4 最优PDT存在的一个例子Fig.4 An example to validate existence of optimal PDT

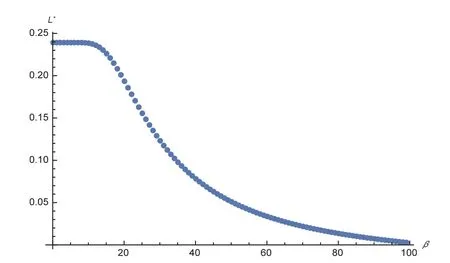
图5 不同有限理性水平下的最优PDTFig.5 Optimal PDT curve in BR level

图5表明:企业的最优承诺交付时间在顾客的有限理性水平上是递减的;在有限理性水平接近0的一段范围内曲线下降得比较缓慢,也就是说,在较低的顾客有限理性水平上,最优PDT对有限理性水平变化的反应不灵敏.在β接近无穷时,最优承诺交付时间接近于0.这说明,企业在进行最优PDT决策时,对有限理性水平较低的顾客采用差别不大的PDT策略,并不会损失多少效率.

5 结束语

本文研究服务系统中顾客有限理性对企业的交付时间决策的影响.在顾客无法准确估计逗留时间的情况下,通过引入顾客有限理性水平参数建立基于时间竞争的有限理性需求率函数,并在此基础上提出企业利润最大化问题.研究表明,有限理性需求率是顾客有限理性水平的减函数;在企业交付成本与交付价格均外生而交付可靠性内生的情况下,最优承诺交付时间存在并且在顾客的有限理性水平上是递减的.

与完全理性的情况相比,基于有限理性需求的承诺交付时间决策有更广泛的适用性.企业可以根据顾客有限理性水平的差异采用有差别的承诺交付时间以达到利润最大化.但是,在应用中得知道顾客有限理性水平参数,需要找到测定该参数的简捷有效的方法.企业在短期中可能出现服务能力不足,因而本文讨论的单个企业的能力无限的要求过高,后续研究可以考虑能力有限,或多个企业竞争时的情况.