不确定性、最优资本结构与投资期权价值

曹启龙,周 晶,盛昭瀚

(南京大学工程管理学院,江苏南京210093)

1 引 言

自Myers[1]提出可以把企业在未来的投资机会看作成长期权以来,关于期权在实物投资中的研究,即实物期权领域的研究一时成为学界的热点.实物期权理论之所以能够引起国内外学界和实务界的强烈关注,在于其相对于传统投资决策方法的三大优势:考虑了投资的不可逆(部分不可逆)性、管理的灵活性以及等待的时间价值[2].以Dixit等[3]为代表的一批学者深入探讨了不确定性、投资时机选择与企业投资期权价值关系及其应用的问题.Bellalah等[4]基于资本资产定价模型研究了不完全信息条件下企业投资的期权价值.Cortazar等[5]的研究是把实物期权理论应用于讨论油田投资的代表作之一.Farzin等[6]开创性的研究了技术采用的最优投资时机问题.Bellalah[7]考虑了存在信息成本的条件下的不可逆性以及沉没成本对企业投资期权价值的影响.Wong[8]研究了不确定条件下的投资时机选择效应,并发现了不确定性与期望投资时间的倒“U”型关系.亢娅丽等[9]基于实物期权理论评估了政策不确定条件下的发电企业投资燃煤发电+CSS技术的期权价值以及主要影响因素.

此后,有学者注意到企业在进行投资时不仅要考虑到投资的时机而且要考虑投资的规模问题.Bøckman等[10]研究了不确定条件下小型水电站的投资时机和投资规模问题,得出了不同项目类型的最优投资时机和最优投资规模.Wong[11]构建出一个连续时间序列模型,研究了不确定性对投资时机和投资规模的影响.Wong[12]基于均值回归模型研究了投资时机和投资规模对放弃期权投资的影响效应.国内学者李应求等[13]以最大化投资机会价值为基点,在不确定条件下构建了最优投资时机和最优投资规模的模型,并用数值解研究了其变化规律.李强等[14]基于实物期权的方法研究了企业融资能力对企业技术创新投资决策的影响.阳军等[15]基于实物期权理论,研究了不变产出和可变产出条件下企业最优投资时机和最优投资规模的解析表达式,比较了不同条件下的企业投资决策问题.

通过上述综述和分析可以看出,学界对企业在不确定条件下的投资决策问题主要是从两个方面展开的:投资时机和投资规模的选择.然而,当涉及到企业投资规模的问题时,一个不得不面临的问题是企业资金的来源,即股权融资与债务融资的权衡问题.根据资本结构权衡理论[16-18],企业进行债务融资有两个方面的效应:债务融资产生的债务利息是免税的,即负债能够产生“税盾效应”,增加企业的价值;但同时负债过多,破产的风险也就更大,这一不利因素降低了企业的价值.这一经典理论认为对于负债企业而言,企业价值是其“税盾”效应与破产风险权衡的结果,并且根据这一权衡过程能够得到最优的负债水平,即最优的资本结构.鉴于现实中几乎不存在不负债的企业,因此更为现实的问题是考虑不确定条件下,企业负债时的最优投资时机和最优投资规模选择的问题.

考虑到不确定性、资本结构水平对企业价值的重要影响,本文基于实物期权理论和资本结构理论研究在企业负债的条件下,企业投资时机、投资规模的选择问题及其对企业投资期权价值的影响.本文的研究有三个方面的新问题:第一,在不同的不确定条件下即不同的资产价格波动水平下,企业最优资本结构的选择问题;第二,在不同的不确定条件下,负债企业与非负债企业投资期权价值的差异性问题,即债务是否增加了企业的投资期权价值;第三,负债企业在不同的资本结构情形下,最优投资规模和最优投资时机的选择问题.本文的研究既得到了与已有研究相一致的结论,即随着企业面临风险不确定性的增加,企业投资期权的价值亦会增加,也得到了更多的新的结论,具体为对应上述问题的三个方面:1)当资产价格的波动率在一定的范围之内时,不确定性与资本结构是正相关的关系,而一旦超出某个临界点,不确定性的增加将导致企业资本结构剧烈的下降;2)负债企业和非负债企业投资期权的价值虽然都随着资产价格波动率的增加而增加,但二者增加的趋势和幅度是不同的,并且不确定性的程度在一定的范围之内时负债企业投资期权的价值大于非负债企业投资期权的价,而一旦超过了某一临界点,则正好相反;3)企业负债水平的增加能够推迟企业的投资时机但会增加企业投资的规模,并且企业投资规模增加的幅度要大于企业投资时机的幅度.

2 企业负债与投资决策

企业在进行投资决策时通常要面临如下问题:1)何时投资;2)投资多少;3)如何融资.假设企业投资时机的选择与其产品的预期市场价格产品严格相关,即当产品价格较低时不投资,当产品价格上升到某一水平之后,可以“触发”企业进行投资.假设产品的产出价格为p,并且p服从几何布朗运动,即

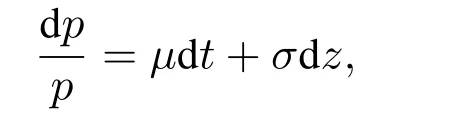
其中u和σ分别为产品价格的预期增长率和波动率,z为维纳过程.

根据柯布道格拉斯生产函数,企业的产出与投资的关系为Q=ALαKβ,其中Q为产出水平,A为技术水平,L为劳动力投入,K为资本投入,α和β分别为劳动力和资本产出的弹性系数.为简化起见,假设企业具有不变的技术产出水平和劳动力投入水平,并且A=1,α=1,则企业的产出完全由其投入的资本水平K所决定,即Q=Ka,0＜a≤1.假设每一单位资本的价格为k,则投资的总成本为kK.根据柯布道格拉斯生产函数,单位时间内的生产能力(产量水平)与投入的资本为指数函数关系,则其投资的总成本又可以写成kQb,b=1/a,由于k和a都是正的常数,Q和K存在着严格的正相关关系,下文将以Q代表企业的投资规模.另外假设企业生产的可变成本为c,税率为τ,现金流折现率为ρ,并且ρ＞µ,企业进行债务融资时支付的债务利息为ϕm,其中ϕ为债务不违约时的债务利息率,m为债务的面值.

2.1 无负债时企业投资期权的价值

为了能够与负债企业的投资决策进行比较,这一小节在文献[19]研究的基础之上首先讨论无负债时企业的投资时机、投资规模以及投资期权价值的问题.企业在没有债务并且持续经营的情形下,其价值为经营现金流的折现值,在企业产品的产出价格为p时,有

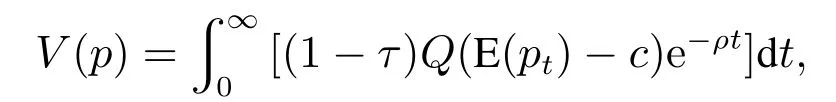
将E(pt)=peut代入上式,可得

式(1)说明,无负债企业的价值为其收入流的现值与支出流的现值之差.

式(1)是非负债企业能够持续经营条件下的企业价值,若假设p∗为企业进行投资的门槛价格,则上式隐含的假设是p＞p∗.根据文献[19],当市场前景不好,产品价格持续下降到p＜p∗时,企业将停止生产,由于非负债的企业不能申请破产,并且产品价格依然存在上升的可能性,因此对于暂时停止生产的企业而言,其再次开始生产的投资机会相当于一个看涨期权,即p＜p∗时企业存在投资的期权价值.由于期权不产生现金流,根据Bellman方程,在时间区间(t,dt)内

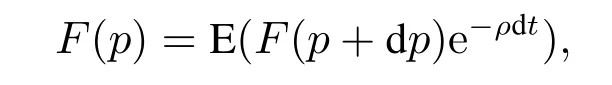
其中F(p)为企业投资的期权价值,计算并化简得

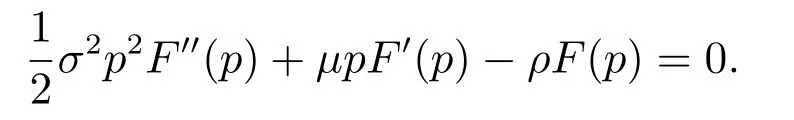
根据文献[2],上述微分方程的解的形式为

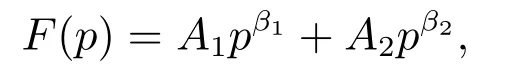
为使得系数A1,A2不为0,表达式F(p)=A1pβ1+A2pβ2还满足如下约束条件

约束条件(2)表示当产品价格p趋近于0时,其再次回复到原有价格水平的可能性非常小,对于企业而言此时已经没有继续等待的价值了,因此其对应的投资期权价值为0.约束条件(3)为价值匹配条件,即在p∗这一点,企业投资期权的价值等于企业投资的最终净回报V(p∗)-kQb.约束条件(4)为平滑粘贴条件1关于价值匹配和平滑粘贴条件的讨论见文献[3]..

由于β2＜0,为满足式(2)需要有A2=0,此时F(p)=A1pβ1.结合表达式价值匹配条件(3)和平滑粘贴条件(4),可得

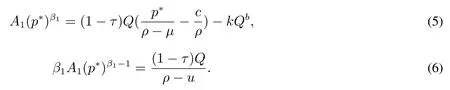
由式(5)和式(6)可得

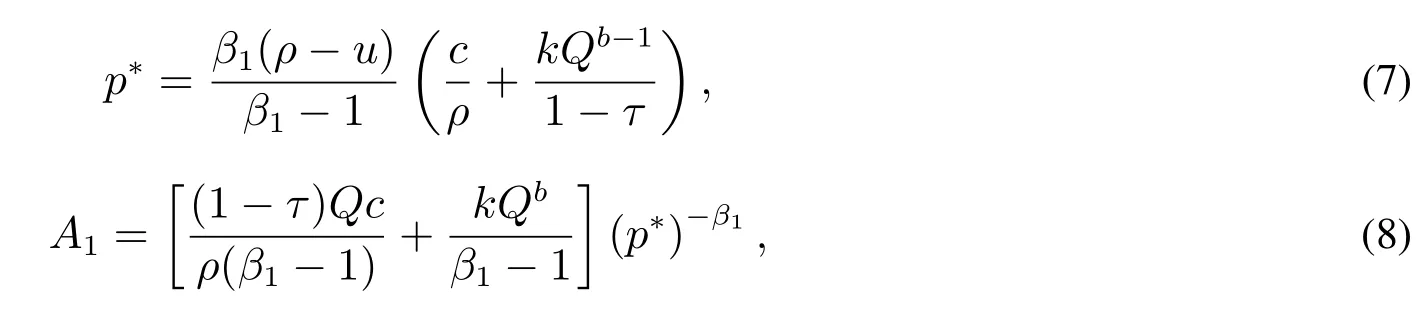
从而得到企业投资期权的价值

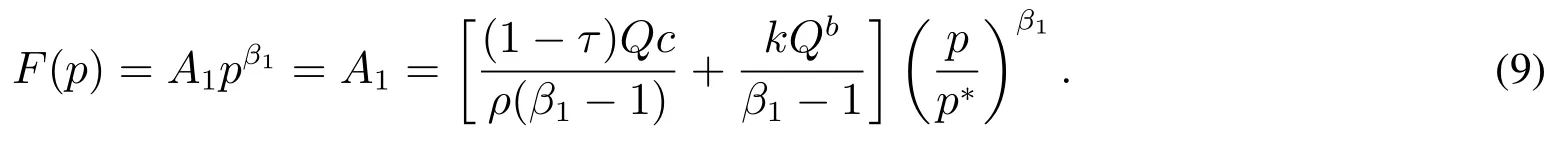
在上述的分析中,将企业的产量Q都是作为给定的外生变量,但在企业的实际生产中,企业必须根据市场的需求不断的调整产量,企业对产量的调整应满足其价值最大化,即给定任意的产品价格水平p,有,计算可得

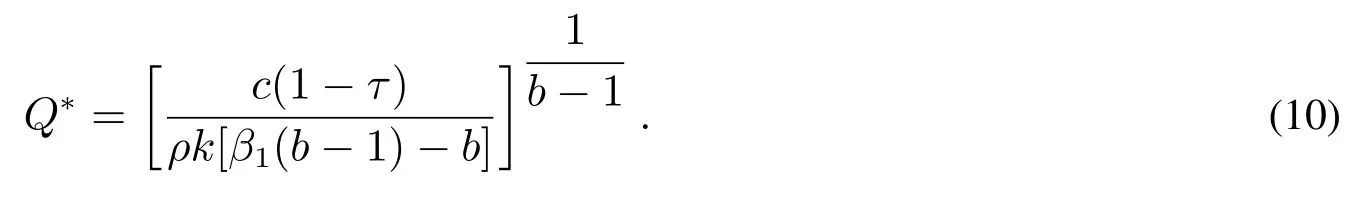
式(7)为企业进行投资时的产品门槛价格表达式,把式(10)代入到式(7)可计算出在企业选择其最优生产规模时所对应的投资价格

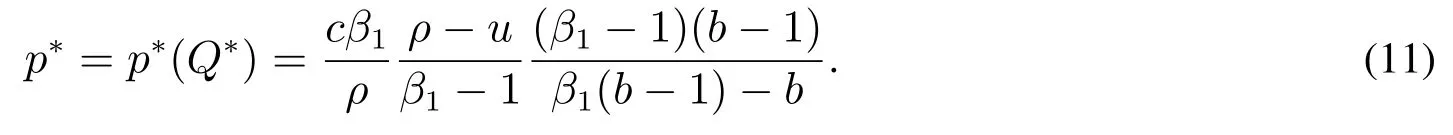
把式(10),式(11)代入到式(9)就可以得到非负债企业在选择其最优投资时机和最优生产规模时的投资期权价值.

2.2 负债条件下的投资时机、投资规模与投资期权价值

虽然目前大多数研究不确定条件下企业投资决策的文献没有涉及到企业的债务问题,但现实中债务融资是企业投资资金的重要来源之一.公司金融理论认为企业负债不仅能够提升企业的市场价值,而且债务的规模和结构也能够影响到企业投资的选择.因此,研究不确定条件下,负债企业投资的时机选择、投资规模以及投资期权价值问题是十分有必要的.

当企业进行债务融资时,假设企业支付的债务利息为ϕm,其中ϕ为不违约时的债务利息率,m为债务的面值.对于负债的企业而言,企业的价值可以分为债务价值和权益价值两个部分[20].下面分别对这两个部分的价值进行计算.首先对负债企业的债务价值进行计算,有

式(12)表示在贴现率水平为ρ的水平下,债务利息的确定现值.由于该现值是确定的，因此用一个固定的参数G来表示.

根据文献[20],当考虑到产品价格波动对债务的影响,即考虑到产品价格下降后的破产风险时,企业的债务价值应该有一定的风险补偿,根据Bellman方程,可以计算出考虑价格波动(破产风险)的债务价值

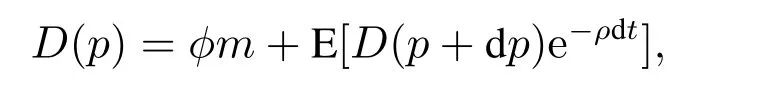
需要说明的是,这里的D(p)表示考虑存在破产风险的债务价值,是一个不确定性的变量,而G是表示债务利息现值的确定性变量,两者是不同的.计算并化简得到非齐次常微分方程

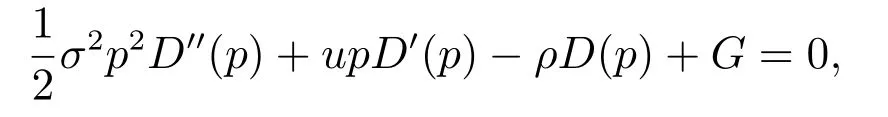
容易得出该方程的解为

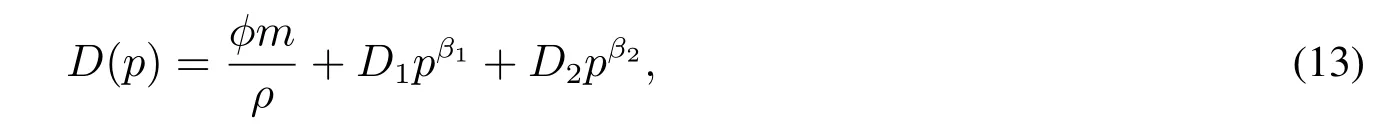
第1项为确定条件下债务的价值,第2项和第3项为考虑到破产情形下的风险补偿价值,D1,D2为待定系数.

同样,在不考虑破产的条件下,企业权益的价值贴现为

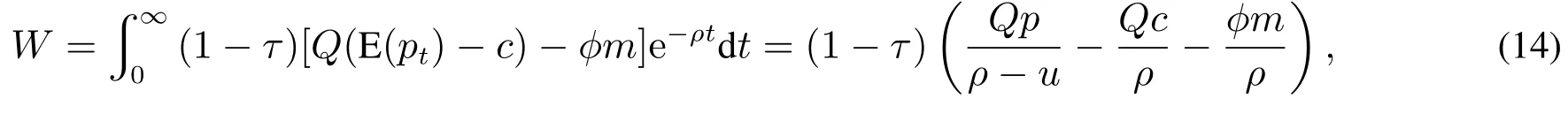
而当考虑到企业破产的风险时,有

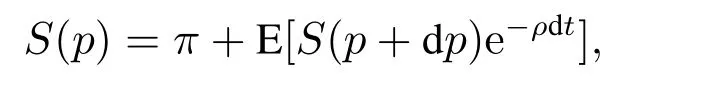
其中π=(1-τ)[Q(p-c)-ϕm.

计算并化简得到常微分方程

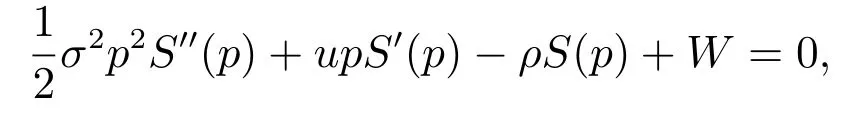
其中S(p)表示考虑存在破产风险的权益价值,是一个不确定性的变量,而W是表示权益价值现值的确定性变量,两者是不同的.该方程的解为

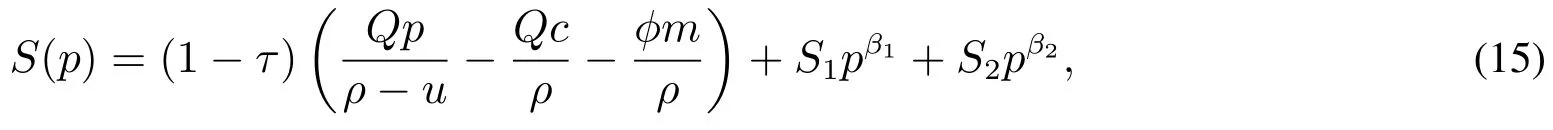
第1项为无风险条件下债务的价值,第2项和第3项为考虑到破产情形下的风险补偿价值,S1,S2为待定系数.

方程(13)和方程(15)分别表示考虑破产风险时,负债企业的债务市场价值和权益市场价值,两个方程式共有D1,D2和S1,S2四个待定系数.为了能够得到待定系数的解,依据Sarkar[20]的论述,当p→∞时,企业破产的概率几乎为0,此时附加于债务价值和权益价值的破产风险补偿也趋于0,因此当p→∞时,有

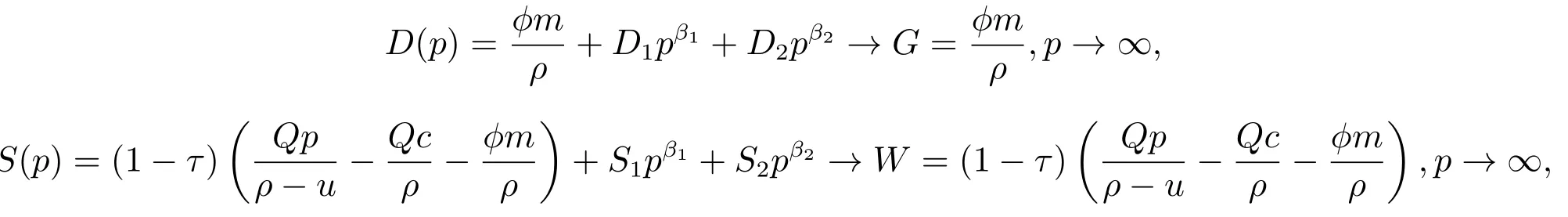
由于β1＞1、β2＜0,为得到收敛解,需要有D1=0,S1=0,即

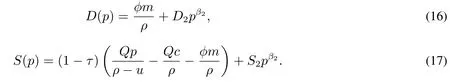
进一步分析当企业的价格持续下降时的情形:当企业的产出价格持续下降到某一价格水平时,企业的收益不足以支付其债务利息,此时企业会申请破产.假设这一破产价格的临界水平为pb,并且当企业破产时,会产生破产成本,假设破产成本占企业价值的比例为λ,0≤λ≤1.在企业破产之后,债权持有者可以得到剩余的1-λ的企业价值,而权益所有者得到的价值为0,因此在pb价格水平上,有以下条件成立

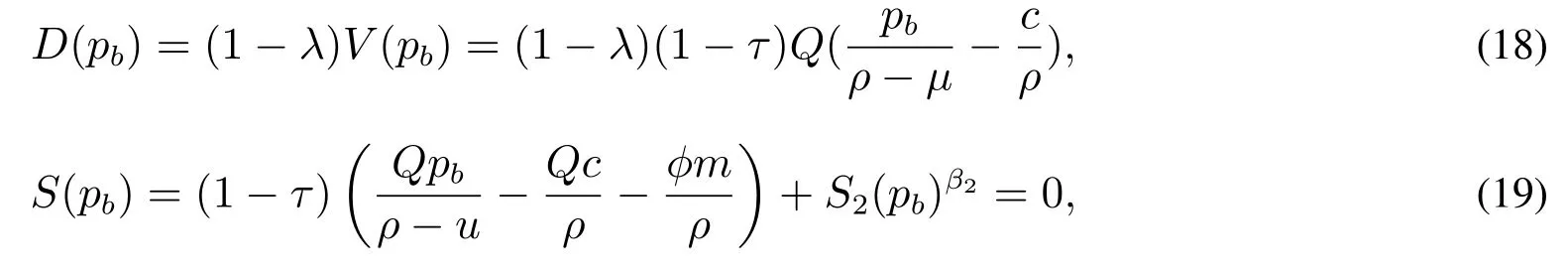
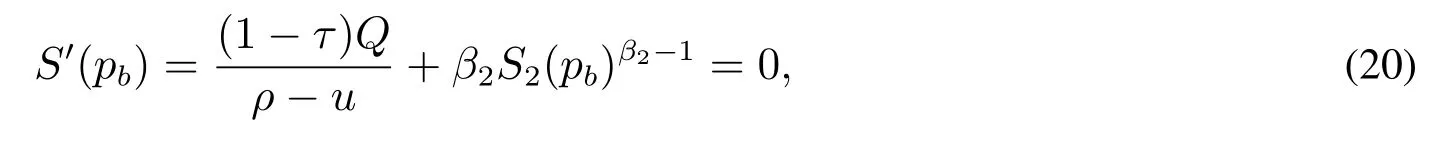
把式(1),式(16),式(17)分别代入约束条件式(18),式(19),式(20),得

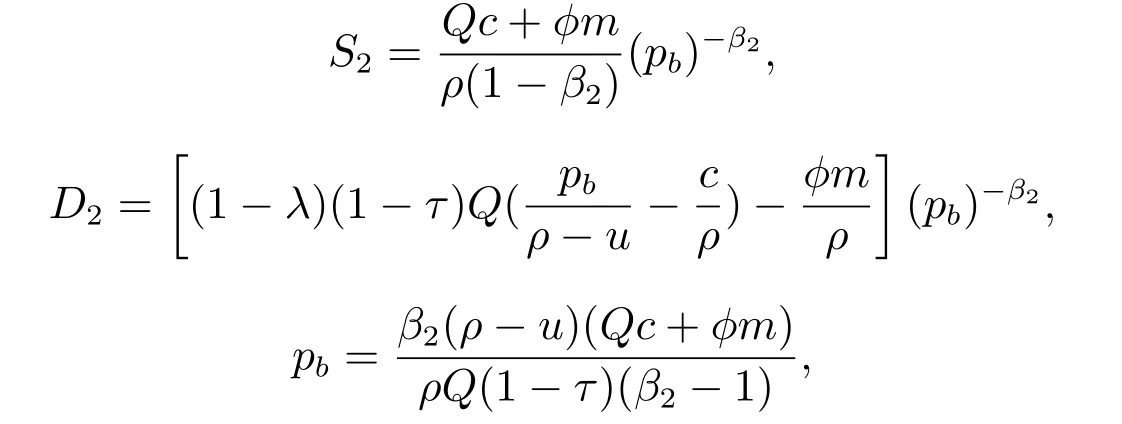
从而

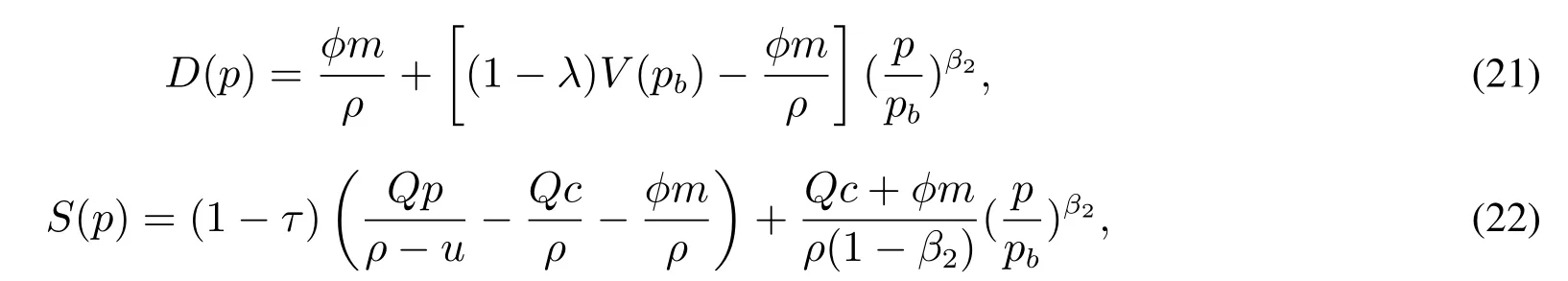
上文分别计算了不考虑负债时,企业的价值和投资期权的价值以及负债时企业的债务价值和权益价值,同样能够继续得出产出价格水平服从布朗运动条件下的负债企业投资期权的价值.

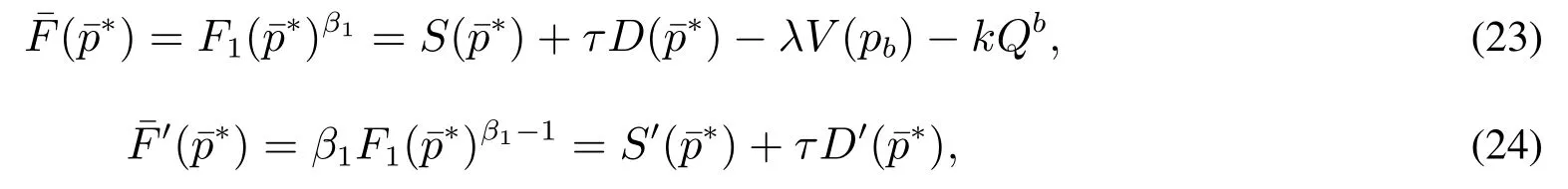
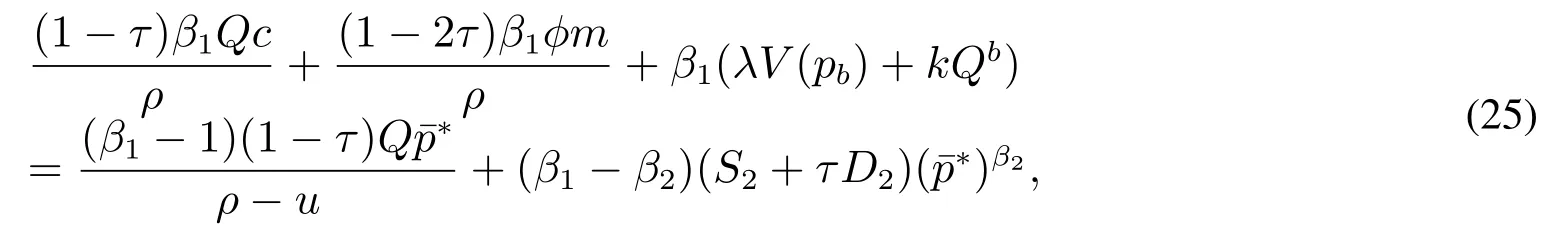
式(25)不容易求得其解析解,但给出常数的参数之后较易获得其数值解,在得到的数值解之后,根据价值匹配条件式(23)很容易求得负债企业投资期权的价值

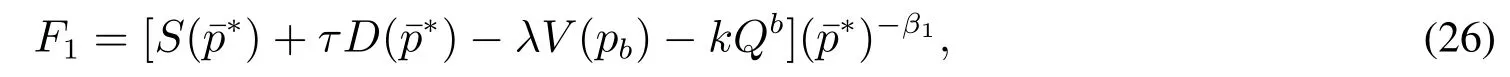
从而

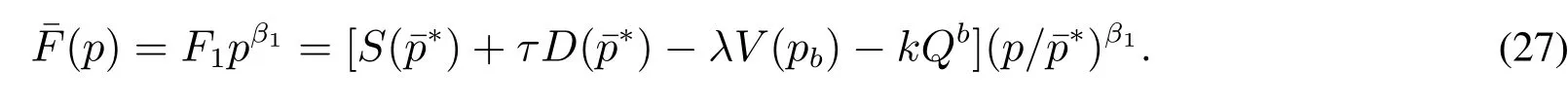
实际生产当中,企业可以依据预期的市场需求调整产量,从而选择最优的生产规模Q.最优的投资水平应该满足在任意的产品价格p下,负债企业投资期权的价值最大化,即.将式(27)对Q求一阶导数,计算并化简得

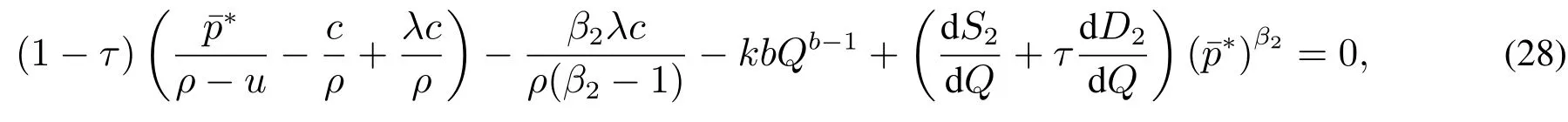
其中

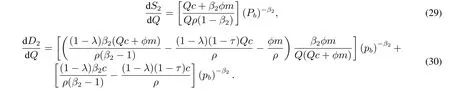
由此,得到了负债企业投资时机选择的表达式(25),负债企业最优投资规模的表达式(28),由于这两个表达式都是非线性方程,不容易求得解析解,将在下文对其进行数值求解.若给定不同的负债水平,并同时对式(25)和式(28)组成的非线性方程组进行求解,可以得到不同负债水平条件下企业的最优投资时机和最优投资规模.把和代入到式(27),则很容易得到不同价格水平下负债企业投资期权的价值.

3 最优资本结构的选择

因为存在税盾的收益效应和破产的风险效应,对于负债企业而言,在投资时不仅要考虑投资的时机选择和投资规模问题,还要考虑企业资本的结构问题,即负债企业的最优资本结构.根据权衡理论,负债企业的价值为权益资本的市场价值加上税盾效应的现值再减去破产成本的现值,而最优资本结构是其税盾效应和破产效应权衡的结果,在最优资本结构水平上,企业的价值应最大化.结合实物期权理论,在不确定条件下,最优资本结构应该满足企业投资期权价值的最大化.若令企业的债务额l=ϕm,则根据本文的说明和假设,企业的最优负债水平应该满足

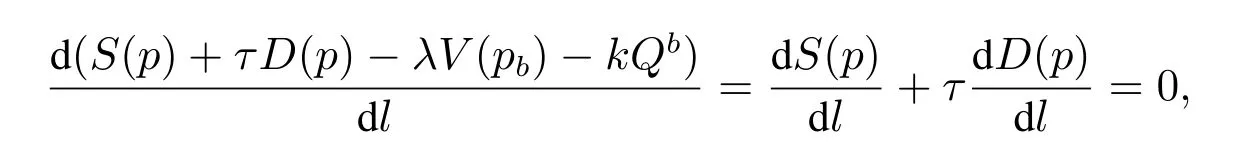
即

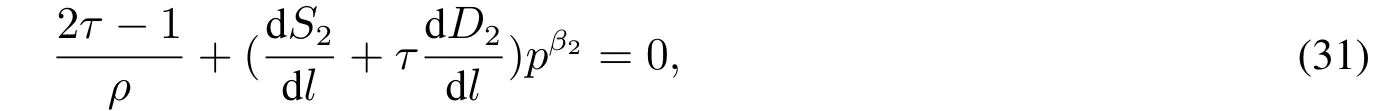
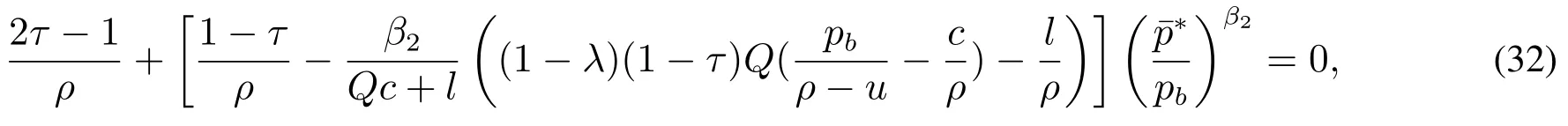
同样对式(32)进行数值求解可以得到使得负债企业投资期权价值最大化的最优资本结构水平.若同时求解由式(25),式(28)和式(32)组成的非线性方程组,能够得到企业进行投资时的最优投资时机、最优的投资规模以及最优的资本结构水平l∗.

4 算例仿真分析

接下来采用数值求解的方法对构建的模型的特征进行分析.参数值的选取参考了Bar-Ilan等[19]的文献,具体赋值为µ=0.01,σ=0.05,ρ=0.06,k=2,c=1,b=2或a=0.5,τ=0.15,λ=0.1.算例仿真主要焦距如下三个方面的问题:第一,在不同的不确定条件下即不同的资产价格波动水平下,企业最优资本结构的选择问题;第二,在不同的不确定条件下,负债企业与非负债企业投资期权价值的差异性问题,即债务是否增加了企业的投资期权价值;第三,负债企业在不同的资本结构情形下,最优投资规模和最优投资时机的选择问题.

图1为负债企业在不同的资产价格波动水平下,企业最优资本结构选择的仿真图.从图1可以看出,在波动率为0的情形下,企业选择的最优资本结构水平为52.16%;此后随着波动率的增加,企业的最优资本结构呈现出平缓上升的趋势,直到波动率为0.73时,最优资本结构达到其临界值0.80;接下来,随着波动率的增加,企业的最优资本结构出现了近乎直线的下降,在波动率为0.91时,企业的资本结构下降到52.16%,即波动率为0的情形,而在波动率接近1.0的情形下,企业选择的最优资本结构为0,此时企业已完全不负债了.从该描述性分析中可以看出,企业的资本结构选择与其资产价格的不确定性有着极为强烈的关系,资产价格的波动率在一定的范围之内时,与资本结构是正相关的关系,而一旦超出某个临界点(本文参数模拟的临界点时0.73),不确定性的增加可以导致企业资本结构剧烈的下降.

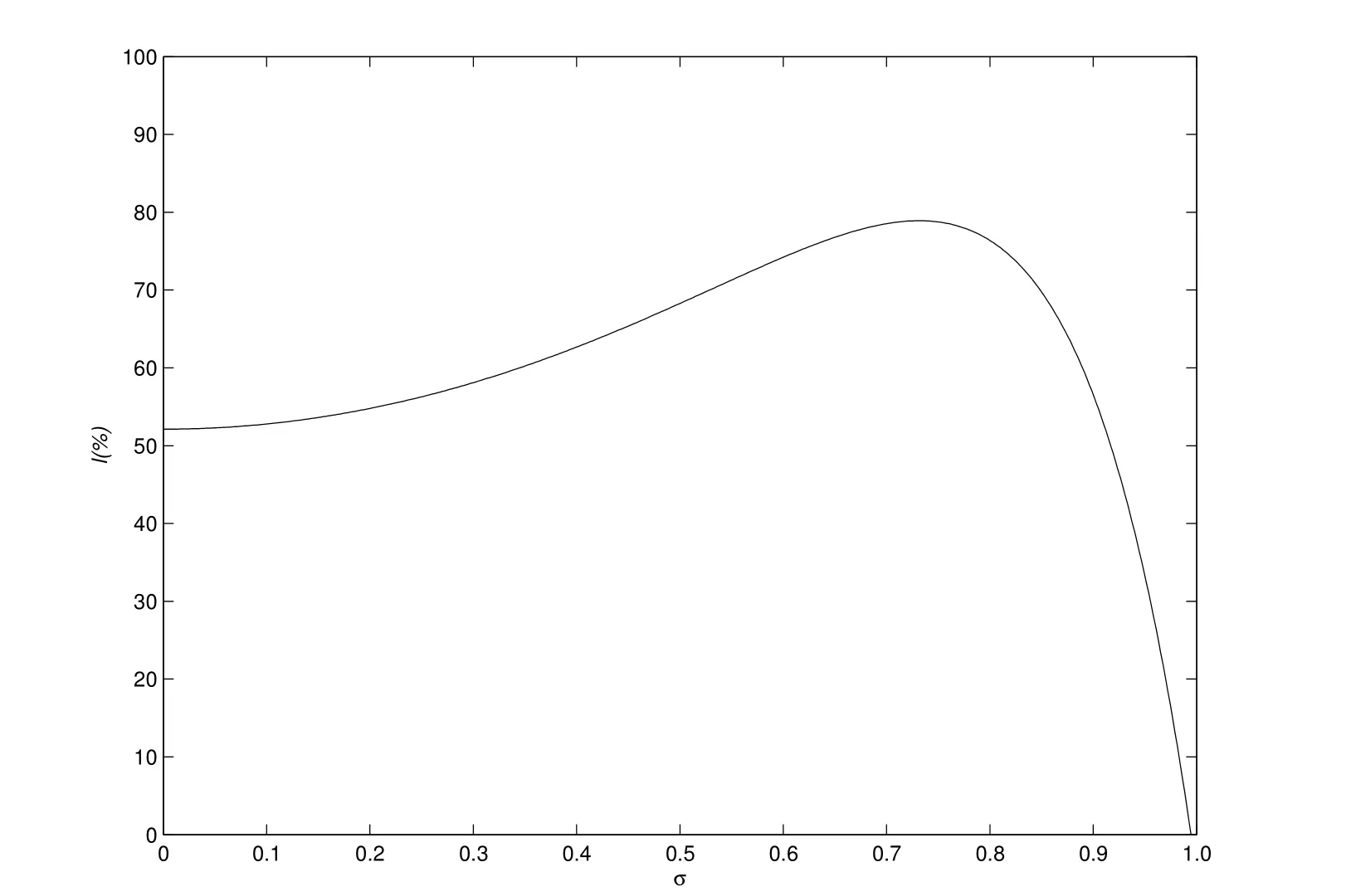
图1 不同波动率水平下企业的最优资本结构选择Fig.1 The optimal capital structure under different volatility levels

图2为在不同波动率水平下非负债企业与负债企业投资期权价值的对比仿真图.从图2中可以看出,在资产价格为0的情形下,负债企业投资期权的价值略大约非负债企业投资期权的价值,随着不确定性程度的增加,负债企业投资期权的价值和非负债企业投资期权的价值都呈现出上升的趋势,但两者增加的轨迹明显不同:负债企业以近似于凹函数的形式增加,而非负债企业以近似于凸函数的形式增加,两者在波动率为0.91处有一个交点.

在Dixit等的研究中,一个经典的结论是:随着企业面临风险不确定性的增加,企业投资期权的价值亦会增加[2,3,7].这一经典结论在图2中得以在此验证,但除此之外,本文创新性的把实物期权理论与资本结构理论结合起来,考虑了现实中企业存在负债和破产风险的情形下其投资期权价值的问题.在得到与经典理论相一致的结论的同时,本文的模型还得到了一些新的结论:1)负债企业和非负债企业投资期权的价值虽然都随着资产价格波动率的增加而增加,但二者增加的趋势和幅度是不同的;2)在波动率小于0.91的情形下,负债企业投资期权的价值大于非负债企业投资期权的价值,而在波动率大于0.91的情形下,正好相反.负债企业投资期权的价值之所以会小于非负债企业投资期权的价值根源在于不确定性太高,不确定性在一定范围之内可以提高负债企业和非负债企业投资期权的价值,而一旦不确定性程度超过了某一临界点(本文参数模拟的临界点时0.91),对于负债企业而言其面临的风险大大增加,企业会迅速降低其负债的水平,从而债务税盾的价值迅速下降,加之高度不确定性情形下企业破产风险的增加,一同降低了负债企业投资期权的价值.

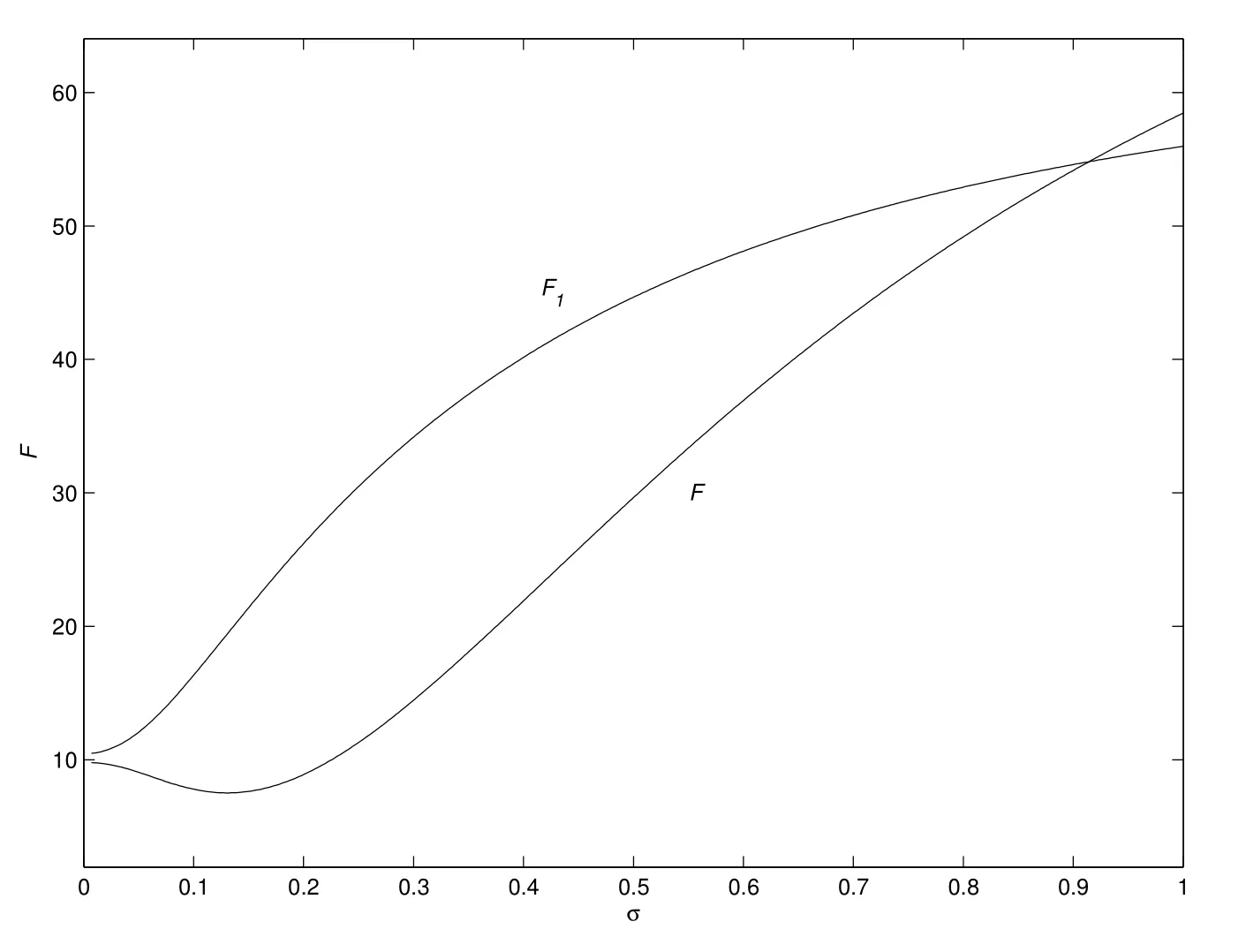
图2 不同波动率水平下企业投资期权的价值Fig.2 The value of option to investment under different volatility levels

文献[3]研究了非负债企业的最优投资时机的问题,但并没有涉及到投资规模和企业的债务问题,他们的研究只考虑不同不确定性情形下企业的最优投资时机问题.本文构建的模型不仅同时考虑了企业的投资时机和投资规模,而且分析了债务因素的影响,这一问题的仿真结果如图3所示.

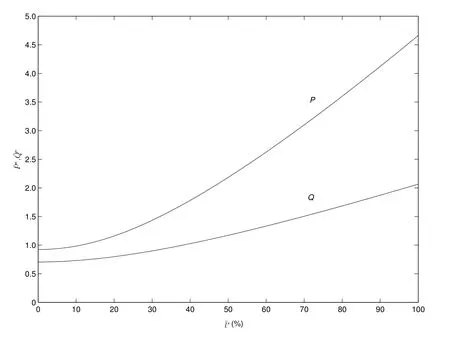
图3 不同资本结构水平下企业的最优投资时机和最优投资规模Fig.3 Optimal timing and optimal size under different capital structure levels

图3为企业在不同的资本结构水平下最优投资时机和最优投资规模选择的仿真结果,横轴为不同的资本结构水平,纵轴为企业的最优投资时机和最优投资规模.从图3中能够看出,随着企业负债水平的增加,其最优投资时机和最优投资规模先是出现了轻微的回落,随后是较大幅度的上升,但企业投资规模上升的幅度较大,而投资时机变化的趋势较为平缓,即企业负债水平的增加最终推迟企业的投资但会增加企业投资的规模,并且企业投资规模增加的幅度要大于企业投资时机的幅度.

5 结束语

现有的研究不确定条件下的企业投资决策的文献较少把企业的负债作为一个重要因素加以考虑,而在实际当中企业负债的规模直接关系到企业投资时机、投资规模的选择以及企业的价值.本文的研究把不确定条件下企业的投资决策与资本结构理论结合起来,引入债务因素和破产成本,研究了不确定条件负债企业的投资时机、投资规模、投资期权价值与最优资本结构选择的问题,同时对比分析了债务因素对在不同不确定性情形下对负债企业和非负债企业投资期权价值的影响.本文的研究认为企业资产价格的不确定性与其资本结构的选择有着极为强烈的关系,并且这两者同时对企业的最优投资决策和投资期权价值产生影响.

把不确定条件下企业的投资决策与资本结构理论结合起来,研究负债企业的投资决策和投资期权的价值问题是一个很有价值的学术问题,本文的研究作为这方面的一个初步探讨不可避免的有着一定的局限性,如模型设计略为复杂,不能求得解析解,而数值解对于参数设置有着较为敏感的变化;另外本文构建的模型均为常微分方程,考虑构建偏微分方程同时考虑价格、债务等多个不确定因素对企业投资决策的共同影响也是下一步的研究方向.