买方“跳单”行为下房产中介差异化定价机制
2018-10-25王晨,龚朴
王 晨,龚 朴
(1.上海商学院商务经济学院,上海200235;2.华中科技大学管理学院,湖北武汉430074)
1 引 言
“跳单”指买方利用中介提供的免费房源信息寻找到合适的房屋,但在已签署《看房合同》后选择绕开房产中介与卖方直接交易的行为.买方“跳单”的直接原因在于不愿意支付过高的中介费,主要体现在两个方面.一方面,我国中介的收费模式主要是按比例收取中介费,这一比例并未随着房价的大幅度增长而减少,反而一直维持在2%~3%未变,因而买方的实际支付大大提升[1],使得买方愈发希望规避高额中介费,“跳单”的动机越来越强.另一方面,买方支付中介费获得的是无形的中介服务,这与支付房款获得有形的房屋有很大区别,且随着房价飞涨,买方支付的中介费增加,但中介提供的服务却未发生任何改变,这种差异使得买方原本就对中介费的支付意愿较低.
驱使买方“跳单”的间接原因主要在于中介的开放性代理模式和不完备的法律体系两方面.在中国,中介代理卖方售房的形式大多为开放性代理[2].该模式下,卖方既可以同时委托多个中介代售同一套房屋,又可自行出售.从而,卖方不仅拥有与“跳单”买方直接交易的权利,还拥有为“跳单”买方隐瞒以保证私下交易不被中介知晓的能力.因此,中介很难从卖方处获得“跳单”买方的信息,无法有效监管房源,为买方“跳单”创造了有利条件.另一方面,即便“跳单”买方交易成功后被中介发现,由于法律体系的不完备,对“跳单”实务的裁定缺乏可供参考的居间法律条款[3],法律约束能力的不足提高了“跳单”买方成功规避中介费的概率.
虽然当前的市场外部环境间接为买方“跳单”创造了便利性,但市场制度的改变并非一朝一夕可以实现,房产中介不能依赖市场制度的改变来改善“跳单”现象.另一方面由于买方选择“跳单”的根本原因是不愿支付过高的中介费,因此,房产中介可以针对具体的交易环境,从运营层面制定更优的中介费决策以应对“跳单”和实现更高利润.基于以上分析,本文将研究当房产中介采取与当前单一定价策略(uniform pricing strategy)相对应的差异化定价策略(differential pricing strategy)时,即针对不同买方的不同交易行为适时适当的调整中介费,能否更好的适应当前房价高企的现状,吸引更多“跳单”买方改选中介交易,以提升总体利润?
房产中介的中介费制定问题一直是国内外学术界的研究热点.Hsieh等[1]的研究表明,固定中介费模式是导致市场无效率的重要原因.近年来,越来越多的研究显示,固定中介费模式已经不合时宜[4].Schnare等[5]指出不应该将中介费固定,而应该由市场决定.Wiley等[6]认为中介费会随着房屋出售的难易程度而变化.秦学志等[7]分析了在房价风险较低的情况下中介机构效益最大化的两部中介费制定策略.Barker[8]则从道德规范的角度出发,得出提高房产中介职业资格和受教育程度要求会促使中介费上涨25%的结论.上述文献表明,有一系列的因素会影响中介费制定策略,制定过程中应该充分考虑这些因素并做适当调整.与以上文献不同,本研究针对中国市场的具体情况,考虑买方“跳单”这一不可忽略的现象,重点研究中介应该如何制定定价策略以应对买方的“跳单”行为.
在买方行为动机上,“跳单”与已受国内外广泛关注的搭便车行为[9,10]相似.搭便车者在坐享他人之利时几乎不付成本且不担风险[11].不同的是,“跳单”者存在被中介发现而支付违约金的可能,同时,由于房屋交易环节复杂,耗时长,在缺少中介居中协调时,“跳单”者还会面临交易失败的风险.因此,与搭便车行为的应对措施不同,中介可以通过制定合理的价格策略在一定程度上克制“跳单”行为,这也是本研究的出发点.目前,对“跳单”问题的研究大多见于法学文献,例如,税兵[12]从解释论层面分析了“跳单”现象;进一步,汤文平[3]探究了“跳单”问题的深层法理,为法律体系的构建做了铺垫.然而,“跳单”对经济决策的影响不可小觑.但仅有于立等[13]从经济学的角度分析了“跳单”行为,发现其与转售价格维持(RPM)互克,并以此为反价格垄断提供政策建议.目前尚未有文献从房产中介的利益角度出发,探讨买方“跳单”行为对价格策略制定的影响,而这一点便是本文的研究重点.
买方“跳单”行为使得中介在付出信息匹配成本之后难以获得收入[14],但现行的单一中介费定价策略无法积极应对这一事实.因此,本研究提出针对具有不同“跳单”倾向程度的异质性买方群体的差异化定价策略模型,探讨中介实施差异化中介费策略的条件及影响因素,并在买方对中介费的敏感度和中介的服务成本变动时,将其与单一定价策略进行比较.
2 房产中介定价
卖方委托中介出售房屋,不失一般性,将售价标准化到[0,1]范围内,假设房屋售价p在[0,1]范围内变动,且服从概率密度函数f(·),分布函数F(·).类比Konishi[15]关于买方支付意愿较高的概率不会太小的假设,假定,这保证了卖方以高价出售房屋的可能性更大,符合现实情况,同时也方便了后续定价策略的分析.买方对该套房屋的支付意愿w服从均匀分布U[0,1],仅在支付意愿w大于p时,买方才会决定购买,但会以θ的概率选择“跳单”与卖方私下交易.由于“跳单”的买方只是不愿支付过高的中介费,并非无力承担中介费,并且选择“跳单”会面临交易失败和被中介发现而追讨违约金的双重风险,因此中介降低中介费可降低买方“跳单”的比例.那么,“跳单”概率θ可设置为中介费k∈(0,v]的增函数θ(k)=αk,其中,v为政府规定的中介费上限.
中介促进买卖双方交易的成本含两部分:提供看房服务的成本,即信息匹配费c1;协调双方达成交易的成本,即服务费c2.无论买方是否购房,中介都需付出成本c1,而成本c2则是在买方通过中介购房之后才会付出.由于中介的定价至少保证在代理最高售价p=1的房屋时,收入能够覆盖服务成本,所以有c2≤k≤v.
下面分别分析单一定价策略和差异化定价策略下房产中介如何制定最优中介费,并提出了差异化策略的具体实施步骤.
2.1 单一定价
单一定价策略下,中介会将买方的“跳单”倾向考虑在内来制定中介费,但不会变动价格来获取更多利润.即,无论买方是否“跳单”,单一定价策略下,中介都会收取同样的中介费.因此,中介面对的优化问题为
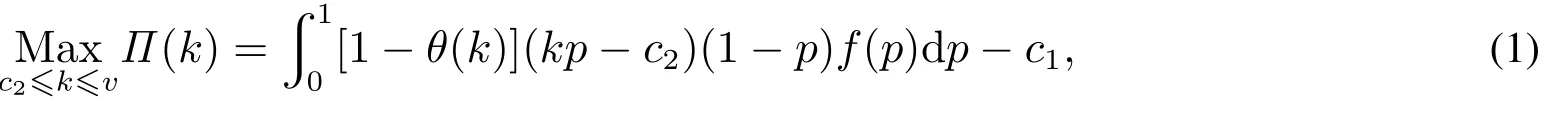
其中1-p是买方愿意购买房屋的概率,1-θ(k)是买方不“跳单”的概率,kp-c2是信息匹配之后,买方通过中介购房时中介获得的利润.
命题1单一定价策略下,利润函数Π(k)是关于k的凹函数.最优的定价策略为:若α≤α0,那么k∗=v;若α≥α0,那么
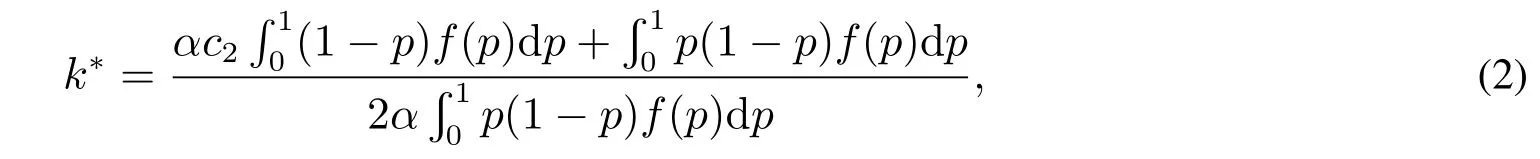
证明由于
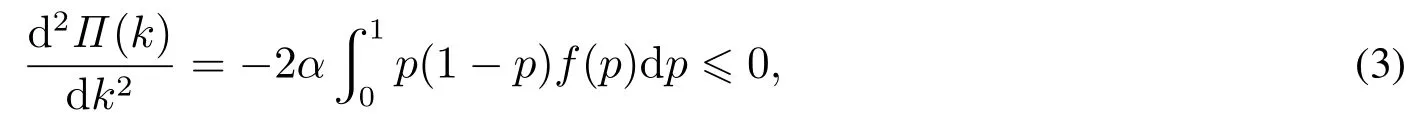
那么函数Π(k)为凹函数,最优解在一阶导数为0处或者边界点处取得.
首先
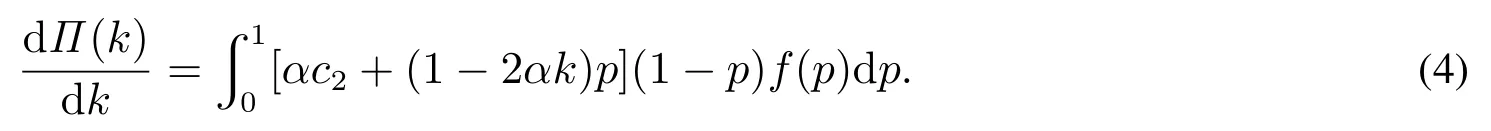
由于αc2≤αv≤1,所以
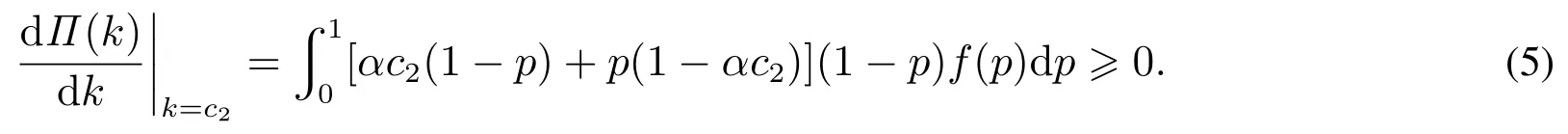

所以
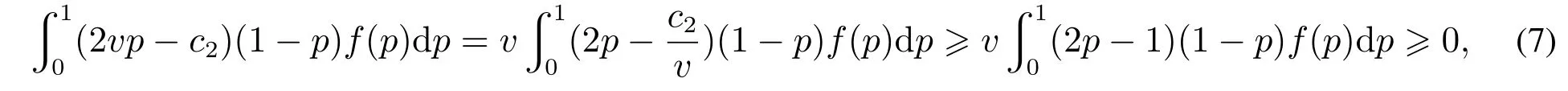
那么α0为正.
因此,α≤α0保证了,根据式(5),对∀k∈[c2,v]可得,所以k∗=v;而若α≥α0,类似可得k∗满足,即结论成立. 证毕.
α越大,说明在同样的中介费下,更多的买方会“跳单”,即买方对中介费更为敏感.那么,命题1表明,在买方对中介费不太敏感时,单一定价策略下中介应该将中介费设置为上限值以获得更高利润.而在买方对中介费较为敏感时,中介需要考虑买方强烈的“跳单”倾向,选择更低的中介费.
2.2 差异化定价
差异化策略下,房产中介会针对有“跳单”倾向的买方额外提供一个较低的中介费,以期望能够降低“跳单”比例,增加收入.较低的中介费是在买方决定不与中介交易之时由中介提出的,计划“跳单”的买方是潜在的接受降价交易的对象,房产中介可以通过这一方式吸引计划“跳单”的买方改为通过中介购买房屋,从而识别出一部分“跳单”买方,提升利润.那么,差异化策略实际上可以描述为两阶段定价模型:第一阶段,中介制定中介费k1;第二阶段,若买方选择不购买房屋p,中介会使用中介费k2(≤k1)进行交易.这样,中介在第二阶段是否一定采取低于第一阶段的中介费,在什么情况下会放弃降价?这正是本节所要研究的问题.
以下采用逆向推导的方式分析差异化策略,首先考虑第二阶段中介费k2的制定.在第二阶段,买卖双方的信息匹配已经完成,因此不需要考虑成本c1,同时,房屋售价p已经实现,中介可针对不同的售价制定相应的k2.因此,中介在第二阶段的优化问题为
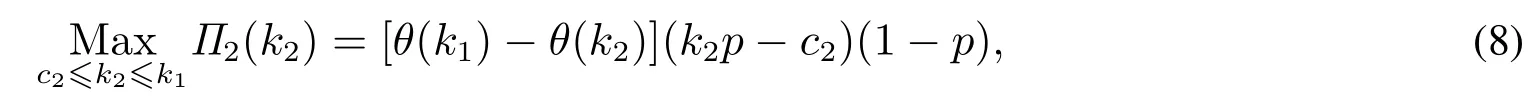
其中1-p是买方愿意购买房屋的概率,k2p-c2是买方在第二阶段购房后中介获得的利润,θ(k1)-θ(k2)是买方由“跳单”改为通过中介交易的人数比例.
命题2差异化策略下,利润函数Π2(k2)是关于k2的凹函数.第二阶段的定价决策如下:当k1p≤c2时,k2∗=k1;当k1p≥c2时,.
证明由于
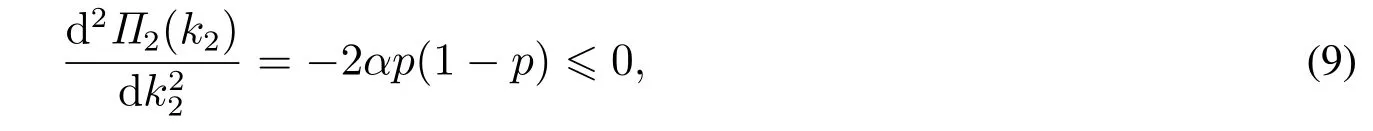
那么函数Π2(k2)为凹函数,最优解在一阶导数为0处或者边界点处取得.
由于
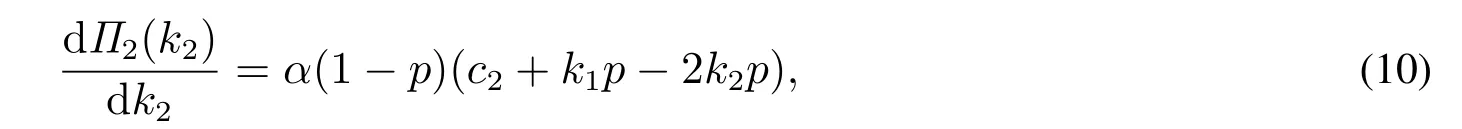
根据命题2,中介在第一阶段所要求的中介费收入k1p会对第二阶段的价格策略产生影响.若要求的中介费收入k1p较高,足以弥补服务成本,那么中介在第二阶段会适当降价,且房屋售价越高,中介费降得越低,以此吸引“跳单”买方改用中介交易,提升利润.若要求的中介费收入k1p无法弥补服务成本,中介不会再降价来对“跳单”买方作任何挽留.
下面分析房产中介在第一阶段的定价.中介在第一阶段的优化问题为
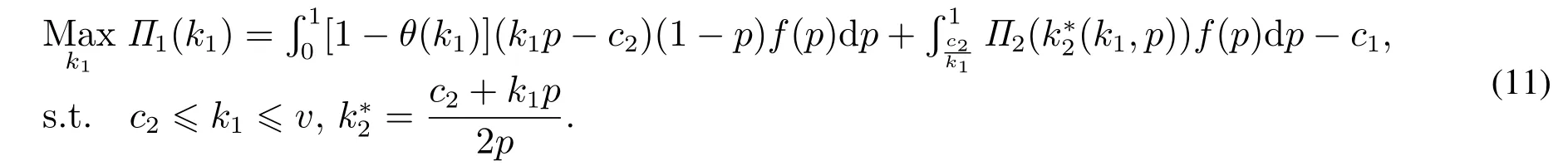
命题3差异化策略下,利润函数Π1(k1)是关于k1的凹函数.第一阶段的定价决策如下:当α≤α1时,k1∗=v;当α≥α1时,k1∗满足,其中
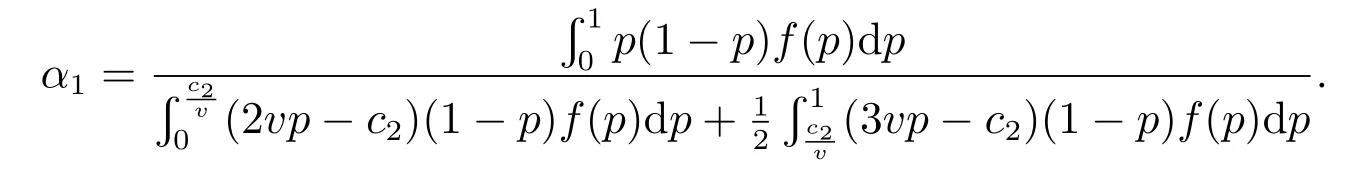
证明由于
所以,函数Π1(k1)为凹函数,最优解在一阶导数为0处或者边界点处取得.
由于
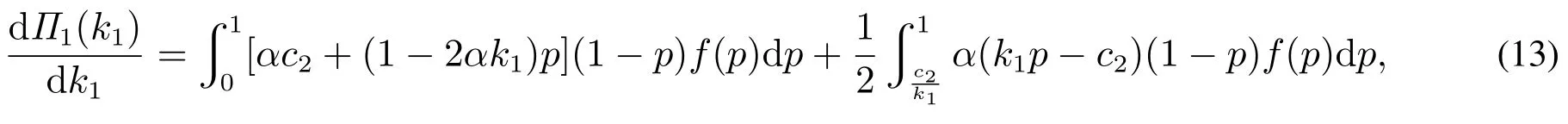
根据2p-1≤p,那么
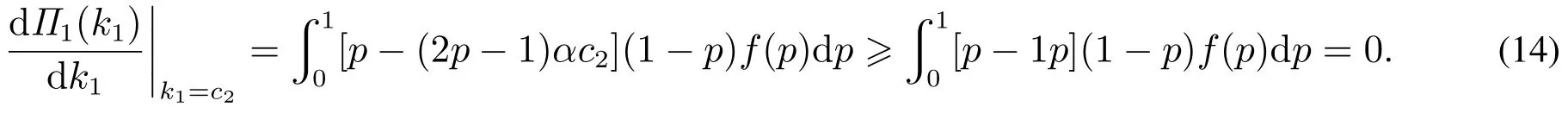
又根据式(6)可得
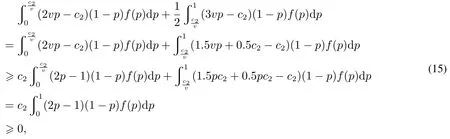
那么α1为正.因此,α≤α1保证了,所以最优中介费k1∗=v;而若α≥α1,则k1∗满足. 证毕.
命题3给出了差异化策略第一阶段中介费的制定原则:在买方对中介费的高低情况不太敏感时,中介应该将中介费设置为上限值;而若买方对中介费较为敏感时,则应该制定较低的中介费.差异化策略第一阶段的定价思路与单一中介费策略类似,但是,在降价条件和幅度上会存在区别,这一点将在3.1节对两种策略的中介费比较中详细说明.
根据以上分析,现将差异化定价策略的实施方案归纳如下.策略实施过程中,中介分别需要根据两个判定条件来制定两个阶段的中介费.首先是外部市场条件—买方对中介费的敏感度α,该敏感度越低,中介在第一阶段应制定越高的中介费.若第一阶段买方通过中介交易,中介能够获得较高的中介费收入k∗1p.若第一阶段买方未交易,那么中介就考虑是否在第二阶段降低中介费,这就涉及第二个判定条件—具体房屋情况.仅当对于房屋售价p来说,中介第一阶段可得的中介费收入k∗1p较高时,即k∗1p≥c2,中介才应降低中介费.并且,房屋售价越高,中介费降得越低.房屋若在第二阶段成交,中介最终会获得较低的中介费收入k∗2p.
3 策略比较
下面将理论推导和数值实验相结合,分别从中介费和利润两个方面对单一定价策略和差异化策略进行比较,试图为房产中介的策略制定和具体的定价决策提供指导.
数值实验的参数设置如下:第一,中介费的取值上限v由中介所在地的政府规定,尽管各地政府的规定不同,但大都在2%~3%之间.本实验以北京市为例,政府规定中介费不得超过交易房屋总价的2.2%,因此设置v=2.2%.第二,与理论模型一致,数值实验中依旧将每平米房屋售价的最高值标准化为1,那么信息匹配费c1和服务费c2的数量级约为每平米10-4,因此可设置c1=c2=10-4.第三,房屋售价的密度函数方面,类似于Li等[16],设置为,其中,示性函数在时值为1,否则为0.该设置满足第二节中关于卖方以高价出售房屋的可能性更大的假定.第四,在需要控制α来研究其他参数变动下中介的策略时(图3,图5和图6),为了使分析能够捕捉更全面的现实情况,参考图2(a),设置α=35以使得中介的策略不会固定不变.
3.1 最优中介费比较
与单一定价策略不同,差异化策略下,中介会视具体情况决定是否在第二阶段给出较低的中介费,以此挽回部分有“跳单”倾向的买方.那么差异化策略第二阶段较低的中介费是否一定低于单一定价策略的中介费?而差异化策略第一阶段的中介费和单一定价策略的中介费间又存在怎样的大小关系?这正是本节所要研究的问题.
根据命题1和命题3,在买方对中介费的敏感度α较小时(单一定价策略,α≤α0;差异化策略,α≤α1),中介的最优中介费决策是取上限值2.2%.如图1,随着服务成本的升高,阈值α0和α1均变大,这说明服务成本对中介利润影响较大,即使会造成更多的买方“跳单”,中介也应将中介费提升至取值上限处.并且,服务成本越高,阈值α0和α1的差异越小,如图1,这意味着单一定价策略的决策更易受到服务成本的影响.
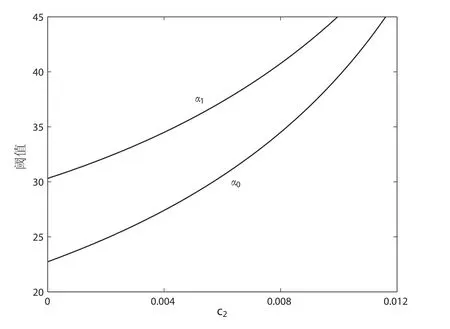
图1 阈值随服务成本c2的变动图Fig.1 Impact of service cost c2on thresholds
命题4各策略下中介费之间的相对大小关系如下:当α≤α0时,k1∗=k∗≥k2∗;当α≥α0时,若p≤p0,那么k∗1≥k∗2≥k∗,若p≥p0,那么k∗1≥k∗≥k∗2.其中.
证明由于,所以
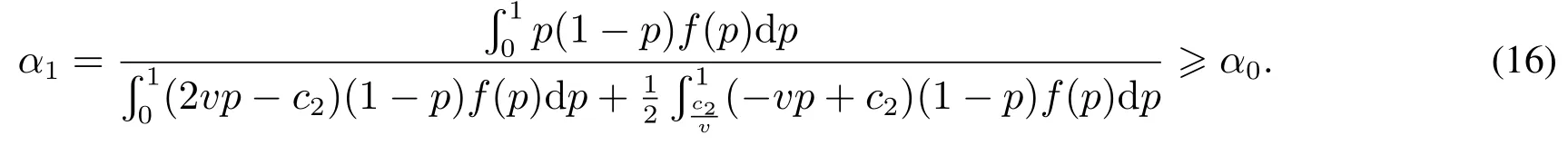
下面考虑α≤α0时的情况.根据命题1和命题3,k∗1=v,k∗=v.又由于k∗2≤k∗1,因此k∗1=k∗≥k∗2.考虑α≥α0时的情况.根据命题1,命题3,k∗满足或k1∗满足0.当k1∗=v时,有k1∗≥k∗.下面分析k1∗满足时,k1∗和k∗的相对大小关系.根据式(3)和式(12)得
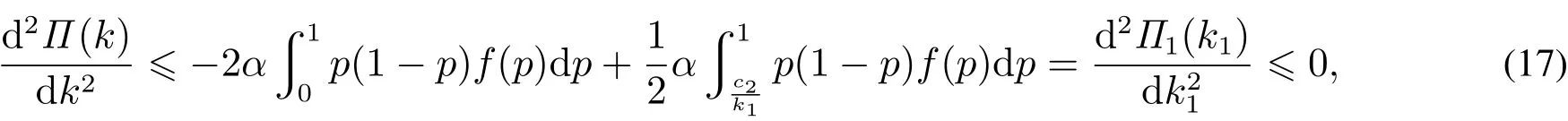
又由式(14)可得
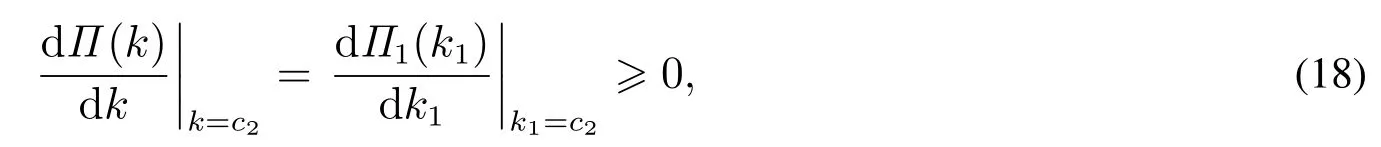
所以k1∗≥k∗.因此,在k1∗的两种取值下,都有k1∗≥k∗.又由于k2∗≤k1∗,所以接下来比较k∗和k2∗.根据命题2,时,有k2∗=k1∗≥k∗.而在p=1时,根据式(2)和αv≤1,有
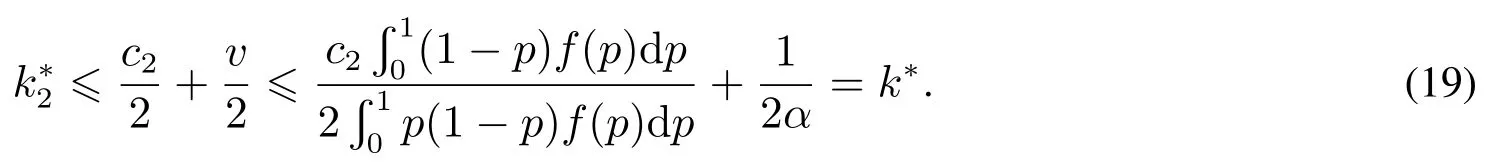
图2给出了命题4的一个数值实例,呈现了随敏感度α的变动,各中介费的相对大小.第一,k1∗和k∗的比较.在α较低时,中介应将二者设置相等,如图2(a).而在α较高时,中介需要降低中介费来降低买方的“跳单”比例.由于差异化策略下中介可设置较低的k2∗来防御“跳单”,因此k1∗下降得较慢,高于k∗.第二,根据命题4,k2∗和k∗的大小关系与房屋售价p有关.在p较高时,k2∗比k∗低,以达到降低“跳单”人数的效果.而p较低时,中介设置的k2∗会高于k∗.这是因为,此时中介实际可得的收入k1∗p难以弥补成本,所以中介只会在保证利润的情形下降低中介费,因而k2∗会高于k∗.这也从侧面体现了差异化策略的灵活性,针对每套房屋都进行了优化.第三,根据命题4,房屋售价p的高低是以阈值p0为判断标准.进一步,图2还表明,随着敏感度α的提升,阈值p0逐渐升高,如图2(b).只有在α高于时,p才会低于p0,如图2(a),差异化策略的k2∗才会高于k∗.另外,根据图2(b),由于阈值p0实际上极小,98%以上的房屋售价都高于p0,因此,在绝大多数情况下,k2∗是低于k∗的.
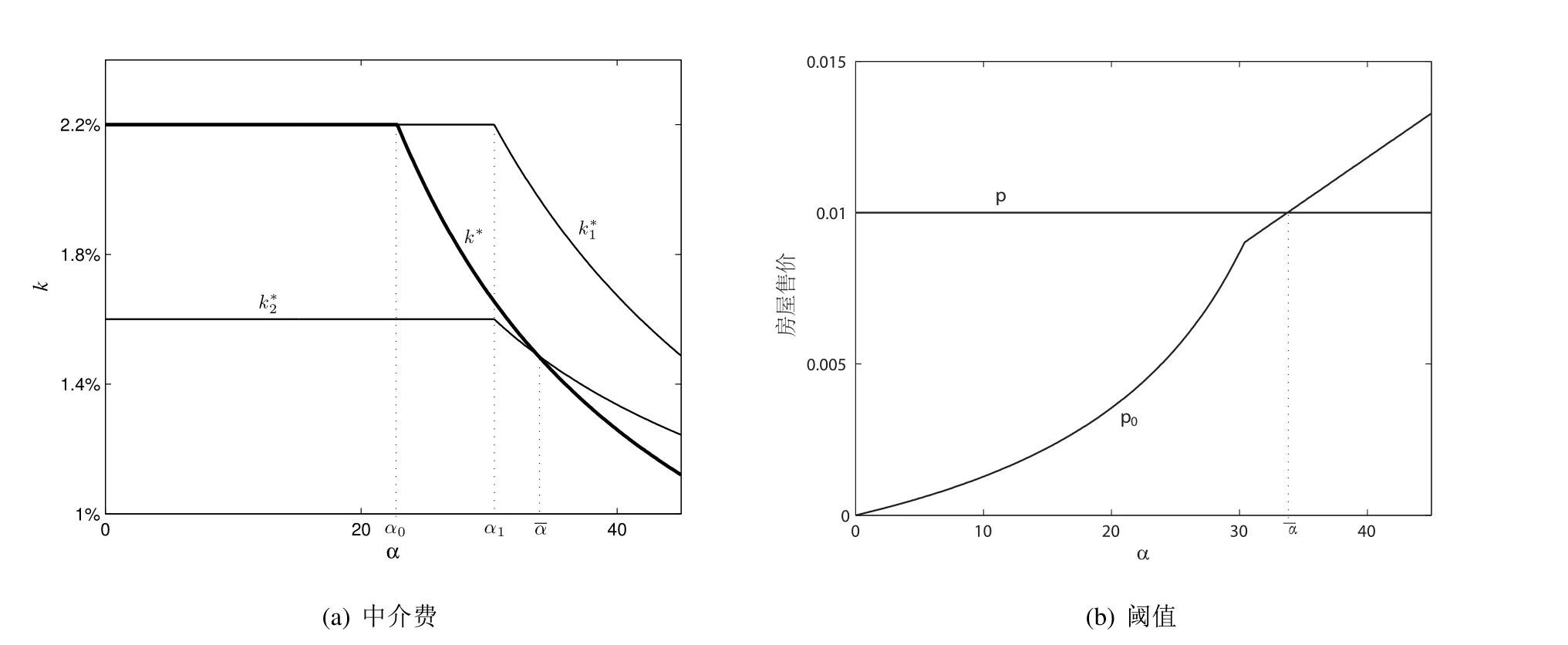
图2 不同中介费的比较分析图Fig.2 Comparison of commissions
图3显示了服务成本c2对中介费的影响.随着c2的升高,为了弥补成本,如图3,两种策略下的中介费都在升高.然而,差异化策略k∗1的上升速度相对较慢.随着c2的进一步升高,两种中介费都会相继达到上限2.2%.
于政府而言,合理制定上限值v对维护市场秩序至关重要.根据上述分析,只有在买方对中介费敏感度较低或服务成本较高时,政府才需要动态调整上限v.否则,中介的最优中介费不会触碰上限,政府无需调整.
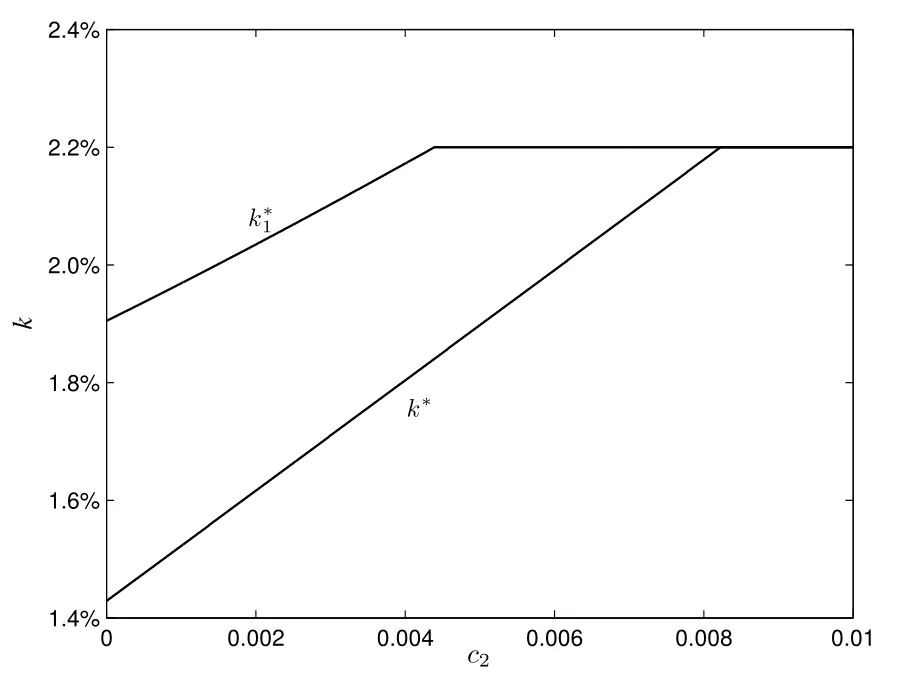
图3 中介费随服务成本c2的变动图Fig.3 Impact of service cost c2on commissions

图4 期望利润随α的变动图Fig.4 Impact of α on expected pro fi ts
3.2 利润比较
本节对两种策略的利润进行比较,并在此基础上给出了中介的最优中介费策略选择法则.
实施差异化策略的利润更高,那么中介是否一定应该使用该策略呢?实际上,与单一定价相比,差异化策略的计算复杂度和实施难度较大,因此,在两种策略的利润无显著差异时,单一定价策略更便于实践操作.
图4和图5分别是中介的期望利润随敏感度α和服务成本c2的变化图.如图4,随着α的升高,由于差异化策略能够挽回一部分“跳单”买方,所以利润下降得较慢.并且,相比于单一定价,差异化策略的利润优势先增大后减小.两种策略下,期望利润都随着c2的升高而降低,如图5.相对而言,差异化策略的期望利润下降得更快.这说明,c2的过高使得差异化策略的优异性能难以发挥.而对于不同房屋p,中介可获得的实际利润见图6.
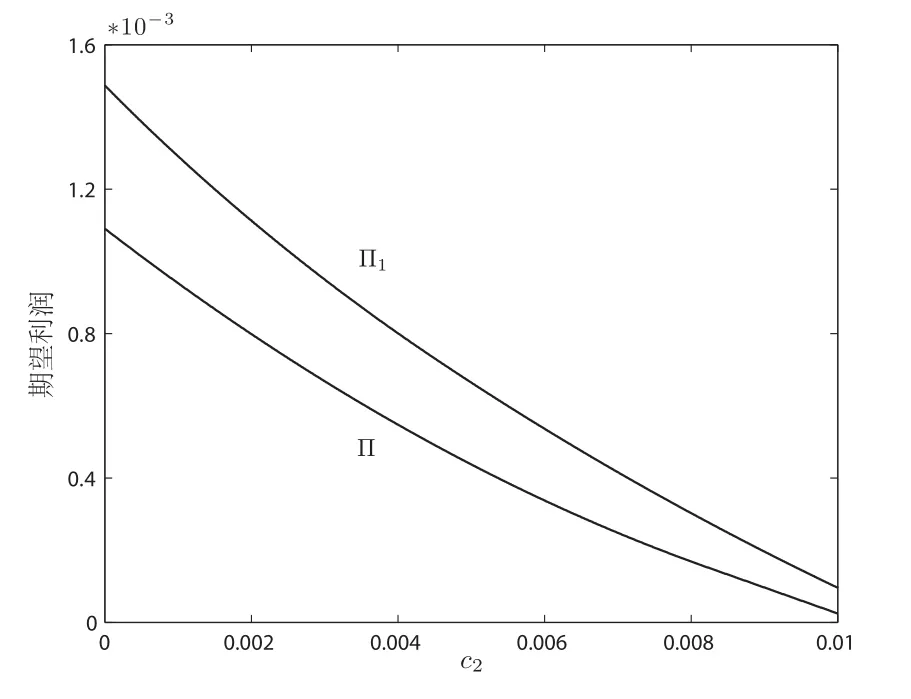
图5 期望利润随服务成本c2的变动图Fig.5 Impact of service cost c2on expected profits
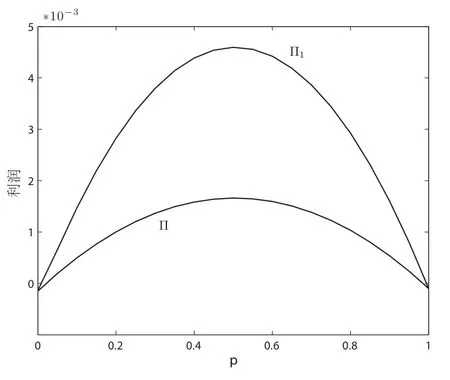
图6 利润随房屋售价p的变动图Fig.6 Impact of p on profits
在p大小适中时,差异化策略的利润优势达到最大.这是因为,在p过高时,愿意购房的买方过少,而p过低时,能实现的中介费收入k∗1p过低,这都缩小了中介可进行差异化定价的空间,难以实现该策略的优势.
基于上述分析,可以得出以下两方面的管理启示:第一,尽管一般情况下差异化策略利润较高,但考虑计算复杂度和实施难度后,中介应在买方对中介费敏感度较小(图4)或房屋售价极高或极低(图6)时,采用单一中介费策略;第二,中介应尽可能降低服务成本(图5)和买方的“跳单”倾向(图4).减少“跳单”的措施如下:可宣传“跳单”的弊病,依靠道德约束买方;可依靠法律,追踪“跳单”买方并起诉;可修改与买方的契约关系,使得买方自愿放弃“跳单”;可从卖方着手,中介牺牲一部分利益,激励卖方签署不与“跳单”买方交易的合约.
4 结束语
针对买方“跳单”行为会对房产中介的利润产生负面影响这一问题,本研究构建了中介费的差异化策略模型,并将其与现时中介大量使用的单一定价策略相比较.结果表明,在买方对中介费敏感度较小时,两种策略下中介费都应提升至最高水平.实施差异化策略时,中介仅在第一阶段要求的中介费收入较高时才应在第二阶段降低中介费,房屋售价越高,中介费应越低.差异化策略第一阶段的中介费一定不低于单一定价的中介费,而第二阶段中介费的大小关系则视具体房屋售价而定.随着服务成本的升高,差异化策略中介费上升的速度较单一定价更慢.除买方对中介费敏感度较小或房屋售价极高或极低的情况外,中介的最优选择是差异化策略.未来可考虑从以下方面进行研究:考虑买方对不同房屋的中介费敏感度不同,或者可多次购置房屋时,中介的最优中介费策略;采用实证研究的方法,探索更多影响中介费定价的因素.
