分位数向量自回归分布滞后模型及脉冲响应分析

许启发刘 曦蒋翠侠虞克明

(1.合肥工业大学管理学院,安徽合肥230009;2.合肥工业大学过程优化与智能决策教育部重点实验室,安徽合肥230009;3.Department of Mathematics,Brunel University,London UB8 3PH,UK)

1 引 言

时间序列分析是一种动态数据分析与处理方法,为揭示决策变量的动态行为特征及其相互之间动态影响关系提供了基本工具,在实践中获得了广泛应用、取得了很好的应用价值,成为一个重要的研究领域.时间序列可以视为随机过程的一次样本实现,其分析方法大体经历了从确定到随机、从一元到多元、从线性到非线性等发展历程.随着差异化统计需求的发展,时间序列平均取值信息难以满足决策需求,如:VaR风险管理侧重于尾部风险特征的描述,人们越来越倾向于研究时间序列完整分布特征的变动规律.为此,在分位数回归框架下进行多元时间序列分析,能够揭示在不同分位点处变量之间的异质影响关系,从而提供更多有用信息,便于科学决策,本文对此开展研究.

为研究多个时间序列之间的关系,Sims[1]提出了向量自回归(vector autoregressive model,VAR)模型.VAR模型采用多方程联立的形式,通过每一个内生变量对模型全部内生变量的滞后值进行回归,从而估计全部内生变量的动态关系,避免了变量内生性与外生性的划分以及模型识别等复杂问题.VAR模型建模过程非常简单,只需进行两个关键性的选择:(1)变量选择,在系统边界范围内,选择关联关系紧密的变量建立模型系统;(2)滞后阶数选择,在可能整数取值范围内,选择能够揭示变量间真实关系的最优滞后阶数.在多元时间序列分析中,VAR模型占据非常重要的地位,一方面它能够同时捕捉多个时间序列之间的线性依赖关系,准确地预测时间序列的动态变化规律;另一方面它可以为许多其他时间序列分析方法提供基础,如:基于VAR模型的脉冲响应分析、Granger因果分析、协整分析等.因此,VAR模型在实践中获得了广泛的应用,如:刘向丽等[2]通过高频数据,使用VAR模型研究了中国期货市场收益率与交易量之间日内变动模式;王曦等[3]使用VAR模型与脉冲响应分析,比较了各种货币政策工具、目标和作用效果,识别反通货膨胀的货币政策有效性;李湘梅等[4]使用VAR模型与脉冲响应分析、方差分解等,研究中国能源消费碳排放影响因素.

然而,以上研究工作都是在均值意义下开展的,只能描述响应变量条件均值的变动规律.按照统计学观点,均值只是随机变量分布的局部特征,当响应变量服从非对称分布或者散布较大时,均值很难具有代表性.完整地描述随机变量变动规律需要依赖于分布函数.为此,Koenker等[5]提出了分位数回归,主要目的在于细致地刻画解释变量对响应变量整个条件分布的影响.王新宇等[6]考虑金融资产收益与正负收益对分位数冲击的非对称性,建立含有非对称绝对值和斜率设定的AAVS-CAViaR模型,采用混合最优化方法估计模型的参数并进行显著性检验.许启发等[7]提出了分位数局部调整模型,实证结果表明,在不同分位点处,调整速度与调整方式都呈现出非对称性.运用分位数回归方法,史金凤等[8]对金融市场稳定进行了检验,王新宇等[9]描述了在不同分位点处IPO收益率与交易量之间的异质性关系.Xu等[10]更进一步使用非线性分位数回归方法,研究了美国非线性Phillips曲线,并给出产出缺口变化对通货膨胀条件概率密度的影响.许启发等[11]使用神经网络分位数回归模拟金融系统的非线性结构,同时结合极值理论弥补非线性分位数回归对极端尾部数据信息处理能力的不足,并将其应用于极端VaR风险测度.这些研究工作一致表明,分位数回归能够弥补均值回归的不足,可以更加细致地描述经济规律在不同分位点处的异质效应,从而提供更多有用信息,便于科学决策.

在时间序列分析领域,均值回归框架下的诸多经典模型与方法,纷纷扩展到分位数回归框架下.Koenker等[12]将自回归模型扩展到分位数回归框架下,提出了分位数自回归(QAR)模型,其自回归系数具有分位点依赖性,随着分位点变化而变化.陈磊等[13]使用分位数自回归(QAR)模型,对石油期货收益率的分布特征与石油市场的风险特征进行了定量研究,发现前期油价涨跌对石油期货收益存在明显的非对称影响.Engle等[14]在QAR框架下提出了CAViaR模型,用于描述风险价值(VaR)的变动规律.Xu等[15]研究了QAR模型对金融危机的预测能力,发现CAViaR模型的预测能力优于QAR模型.Gourieroux等[16]研究了动态加性分位数模型,该模型一方面具有很好的自回归性质,体现分位数的动态效应;另一方面具有很好的包容性,概括了几类经典的线性与非线性分位数自回归模型.叶五一等[17]使用动态分位数回归方法,通过回归系数函数变化趋势对金融风险传染问题进行检验和预测.更进一步,Galvao等[18]在QAR模型中引入外生变量,提出了分位数自回归分布滞后(QARDL)模型.White等[19]将QAR模型扩展到多元情形的向量分析框架下,提出分位数向量自回归(QVAR)模型,可用于讨论不同随机变量尾部之间的关联程度.

本文在QVAR模型基础上,引入外生解释变量及其滞后项,建立高阶分位数向量自回归分布滞后(QVARDL)模型,该模型不仅能够考虑内生解释变量之间的相互影响,而且可以讨论外生解释变量所带来的在不同分位点处的异质影响,从而将White等[19]的QVAR模型向前推进一步.本文主要开展了四个方面新的研究工作:第一,给出了高阶QVARDL(p,q)模型的数学表示及参数估计方法;第二,建立了用于最优滞后阶数p与q选择的信息准则;第三,推导了基于QVARDL(p,q)模型的分位数脉冲响应过程;第四,将QVARDL(p,q)模型及分位数脉冲响应分析应用于解释美国次贷危机的影响.研究结果显示:本文的模型与方法能够同时刻画多个时间序列在多个分位点处条件分位数之间的关联关系,可以更加深入地揭示美国次贷危机带来的影响,实证结果表明:美国次贷危机在世界范围内产生了深远影响,但对不同国家(地区)的资本市场在影响程度、影响方式、响应时期等方面有着不同的表现.

2 QVARDL模型

2.1 模型表示

考虑一个由Y1t,Y2t,...,Ynt组成的n×1维向量时间序列,记Ωt为由生成的直到t时刻的信息集.在给定Ωt-1时,Yit的条件分位数可以定义为

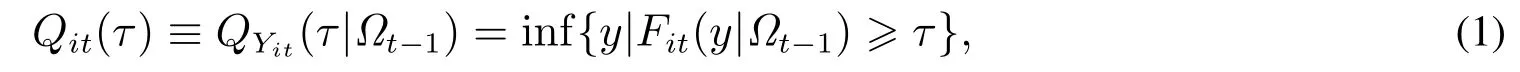
其中τ(0＜τ＜1)称为分位点;Fit(y|Ωt-1)=Pr(Yit≤y|Ωt-1)为随机序列{Yit}的条件分布函数;inf{x}表示变量x的下确界.

Koenker等[5]提出了分位数回归方法,用以估计条件分位数.在时间序列分析中,自回归是最为常用的一个建模方法,它能够很好地描述时间序列的动态性.Koenker等[12]将自回归模型扩展到分位数领域,让自回归系数随着分位点的变化而变化,提出了分位数自回归(QAR)模型.在QAR模型中,响应变量为时间序列的条件分位数,解释变量为时间序列的滞后项.更进一步,Engle等[14]在QAR框架下不仅使用时间序列的滞后项,也使用了条件分位数滞后项,提出了CAViaR模型,取得了更好的实证效果.

受Engle等[14]建模理念的启示,本文将分位数自回归模型扩展到多元情形,建立分位数向量自回归分布滞后(QVARDL)模型,同时估计多个时间序列在多个分位点处的条件分位数及其相互之间动态关联关系.不妨考虑由n个时间序列条件分位数组成的n×1维向量条件分位数QYt(τ)≡Qt(τ)=(Q1t(τ),Q2t(τ),...,Qnt(τ))T,可以建立模型

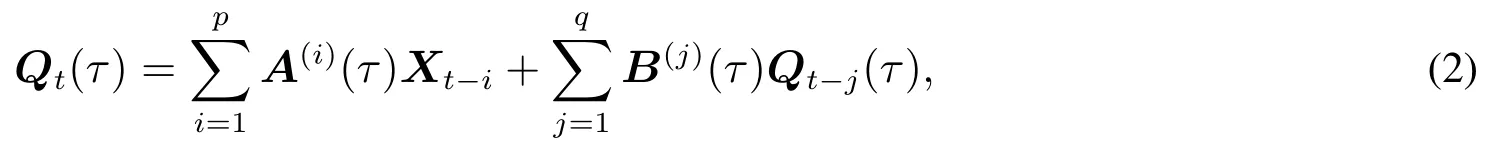
其中X既可以表示由外生变量组成的向量,也可以特指模型内生变量组成的向量X≡Y;p,q分别为滞后阶数;A(i)(τ)与B(j)(τ)为影响系数矩阵,依赖于分位点τ的取值,分别定义为

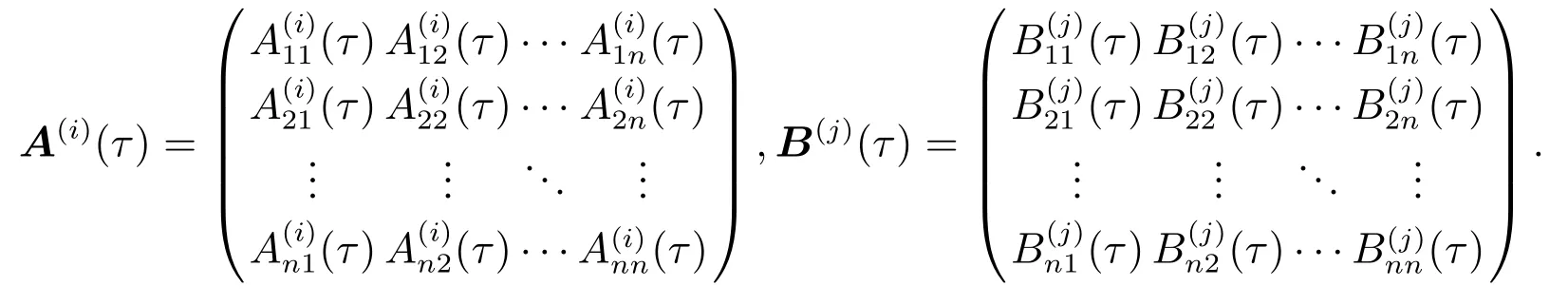
模型表明,向量条件分位数Qt(τ)不仅受到向量时间序列滞后项Xt-i的影响,产生分布滞后效应;同时受到其自身滞后项Qt-j(τ)的影响,产生自回归效应.不过,模型(2)只是考虑了一个分位点,只能估计第τ个条件分位数.如果同时考虑m个分位点τ1＜τ2＜···＜τm处的向量条件分位数,则可以建立模型

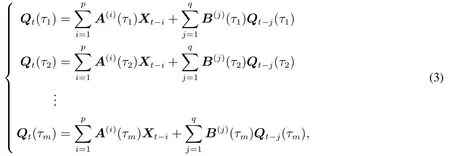
将其表示成矩阵与向量形式

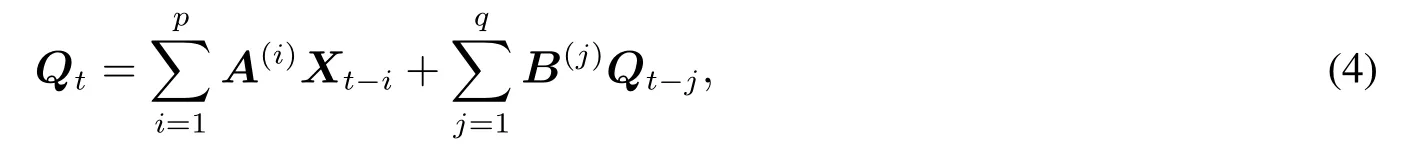
模型(4)与时间序列分析中的自回归分布滞后模型在形式上完全一致,然而却存在本质上的区别,这里的响应变量为条件分位数,回归系数也是依赖于分位点的变化而变化.值得注意,模型(4)是在White等[19]的QVAR模型基础上引入外生解释变量的滞后项所得,是其推广形式,不仅能够考虑内生解释变量之间的相互影响,而且可以讨论外生解释变量所带来的在不同分位点处的异质影响.事实上,模型(4)与Engle等[14]的CAViaR模型也存在显著差别,至少表现在三个方面:第一,这里的响应变量为向量形式,能够同时对多个时间序列的条件分位数进行估计,提高了建模效率;第二,这里的分位点为多个分位点,能够同时考虑在多个分位点处条件分位数的估计,为解决分位数交叉问题提供了可能;第三,这里的回归系数为矩阵形式,若矩阵中非主对角线上的元素非零,则能够刻画不同时间序列之间的相互依赖关系.因此,本文称式(4)为分位数向量自回归分布滞后模型,记为QVARDL(p,q).由QVARDL(p,q)模型,可以得到每一个时间序列在各个分位点处条件分位数估计,其中第i个时间序列在分位点τj处的条件分位数可以表示为

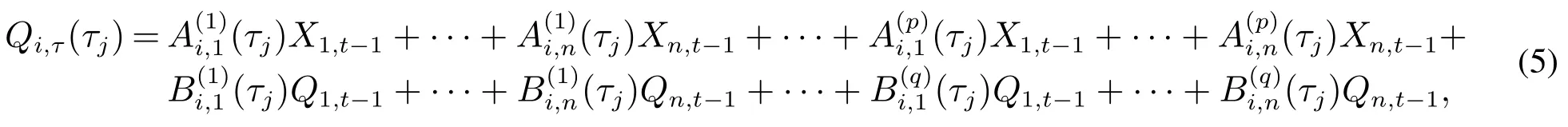
可以看出,QVARDL(p,q)模型不仅描述了时间序列(或条件分位数)自身对自身条件分位数的影响,而且刻画了来自其他时间序列(或条件分位数)的影响,能够度量多个时间序列及其条件分位数之间复杂的相互依赖关系.本文建立了更为一般的高阶QVARDL(p,q)模型,这一高阶模型比White等[19]的一阶QVAR(1,1)模型更能体现变量之间的真实依赖关系,从而更加符合实际建模需求.

2.2 模型参数估计

为实现QVARDL(p,q)模型的系数向量θ的估计,需要将其视为一个模型系统,在多个分位点处同时考虑多个时间序列条件分位数之间的关系.为此,对于样本观测值Yi,t,i=1,2,...,n;t=1,2,...,T,可以定义损失函数S(θ),并由下式实现模型的参数估计

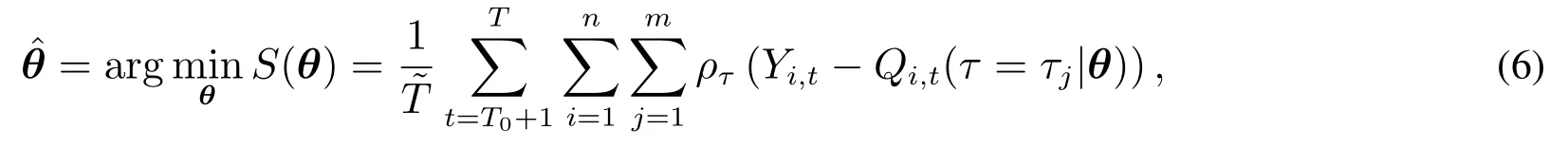
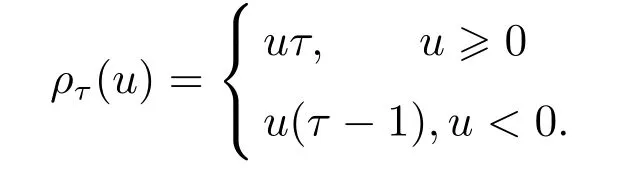
可以证明,式(6)所示的QVARDL(p,q)模型的系数向量估计量具有良好的统计性质:一致性与渐近正态性.

定理1(一致性):对回归系数估计量与真实参数θ∗,有.

证明定理1的证明过程参见附录2.

定理2(渐近正态性):渐近服从正态分布,满足,其中”表示依分布收敛;;▽θ为关于θ的向量偏导数,1{·}为指示函数.

证明定理2的证明过程参见附录3.

2.3 模型定阶

在QVARDL(p,q)模型中,滞后阶数p与q的选择非常重要,可以通过信息准则实现这一目的.信息准则最早由Akaike[20]和Schwarz[21]提出,在实践中获得了广泛的应用,其核心思想为:在模型使用变量数目与模型拟合效果之间进行权衡,以求达到通过最简单的模型结构给出最佳解释效果之目的.传统的AIC和BIC信息准则定义如下:

其中L,k,n分别表示模型似然函数,待估参数个数以及样本量.

为解决QVARDL(p,q)模型定阶问题,本文在分位数回归框架下给出AIC和BIC定阶准则如下:

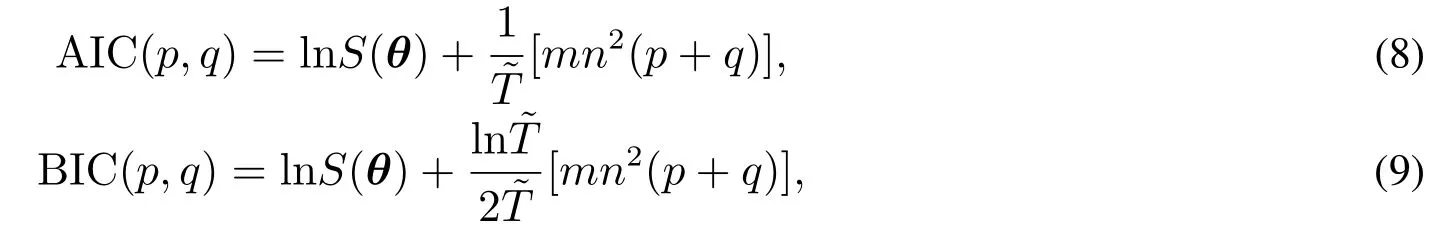
其中S(θ)为按照式(6)定义的经验损失函数,反映模型的拟合效果;待估参数个数取决于p,q,m,n,并且表示为mn2(p+q),反映模型的复杂程度;为实际样本量.使得AIC或BIC达到最小的p,q取值,将作为QVARDL(p,q)模型的最优滞后阶数.

本文给出的信息准则依然沿用了信息准则定义的核心思想,但与传统的AIC和BIC定义也存在不同之处:1)使用经验损失而不是对数似然,来表示拟合效果;2)将对数似然前面的负号,调整为经验损失前面的正号.Yuan[22]和Li等[23]验证了在分位数回归框架下AIC准则和BIC准则的定阶效果,Monte Carlo模拟结果表明:AIC和BIC准则具有与广义交叉验证较为类似的性能,能够获得满意的定阶效果.

3 分位数脉冲响应分析

3.1 分位数脉冲响应函数定义

为进一步考察QVARDL模型系统的稳定性,本文通过对随机误差项ϵi,t实施一个冲击,进而观察各内生变量以及对应的条件分位数的响应情况,称其为分位数脉冲响应分析.在QVARDL模型(4)中,为简化起见,可以不考虑外生变量的影响(取X=Y),仅仅考虑内生变量及其滞后项的影响,从而建立起在QVARDL模型基础上的脉冲响应分析,可以揭示组成QVARDL系统内生变量间动态影响规律,并描述对随机误差项施加一个冲击后,对内生变量在各个分位点处条件分位数的当期值和未来值所带来的影响.

定义1第i个时间序列{Yi,t}在第τ分位点处的分位数脉冲响应函数(QIRF)定义如下

其中δ为t时刻的冲击.在传统VAR模型及脉冲响应分析中,随机误差项ϵi,t服从对称分布,一次性冲击δ常取一个单位的标准差(即δ=1个单位标准差).为简便起见与满足可比性要求,本文依然对随机误差项ϵi,t实施一个单位标准差δ的冲击,来进行分位数脉冲响应分析.

本文给出的分位数脉冲响应函数可以称为伪分位数脉冲响应函数.这里,t时刻的冲击δ仅存在于t时刻,其他时刻并不存在冲击.因此,可以分别给出无冲击时误差项的时间路径为,以及有冲击时误差项的时间路径为.

事实上,本文模型的误差项可能是更为一般的分布函数,如非对称Laplace分布,未必满足对称性要求.此时,可以考虑一个非标准化冲击带来的影响,这一分析在贝叶斯框架下运用贝叶斯分位数回归,更容易得到相应的分位数脉冲响应分析结果,值得未来进一步研究.

3.2 分位数脉冲响应函数估计

考虑如下数据生成过程,用以描述向量时间序列(Y1t,Y2t)T的动态行为

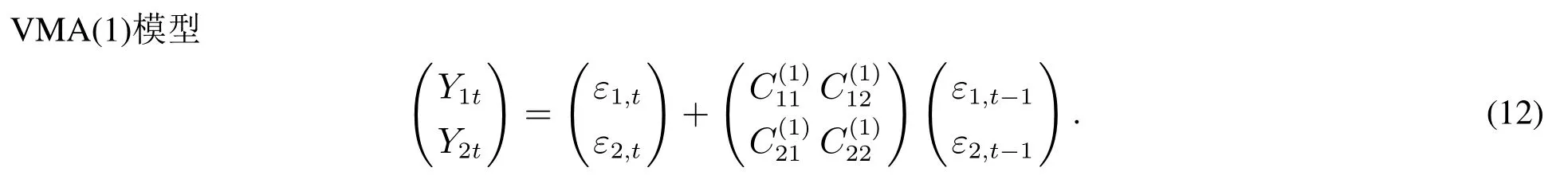
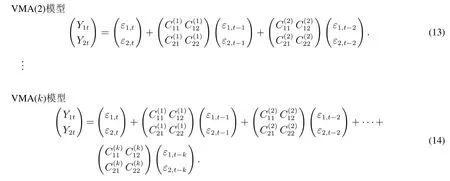
此外,QVARDL(1,1)模型给出的τ分位点表达式

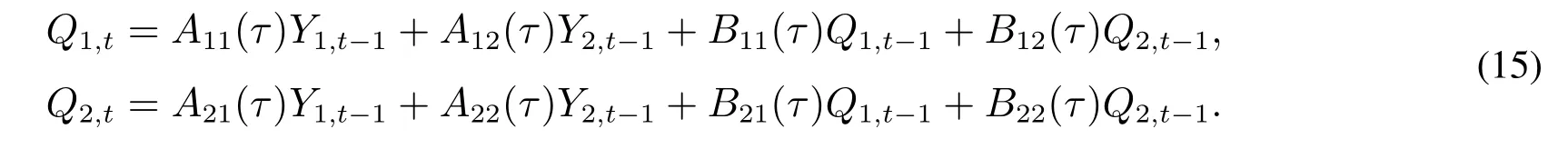
由此,可以通过矩阵形式来表达t时刻二维向量时间序列的分位数

其中Qt与Yt-1均为二维向量,A和B为2×2的矩阵,矩阵元素如上式所示.

1)一阶情形

根据VMA模型设置,t时刻冲击δ仅仅影响Yt,并不影响.进而可以给出有冲击时的时间路径为,此时.

首先,以i=1为例计算分位数脉冲响应函数(QIRF).当s=1时,扰动为常数项,此时只影响,所以有

当s=2时,根据一阶VMA模型设置,扰动同时影响Y1,t和Y2,t,有

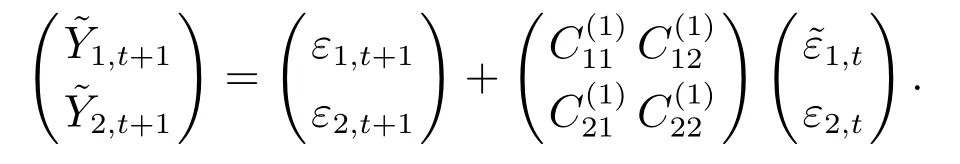
此时,分位数脉冲响应函数可以表达为

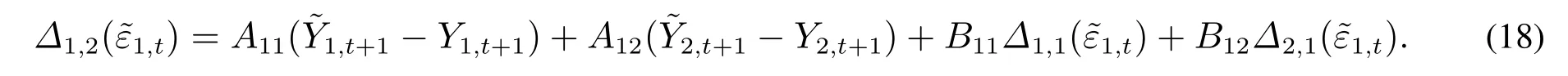
当s≥2时,由于VMA(1)的设置,此时Yt与无关,而对应的条件分位数与有关,有

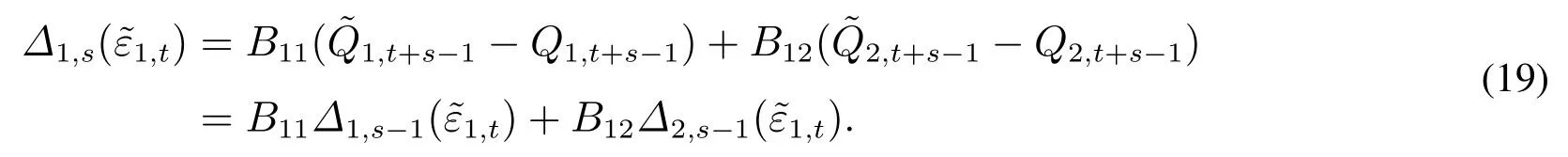
同理,可以得到i=2对应各期分位数脉冲响应函数.当s=1时,有

当s=2时,有

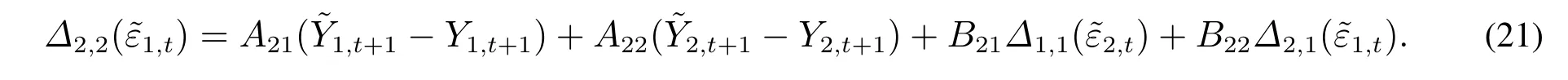
当s≥ 2时,有

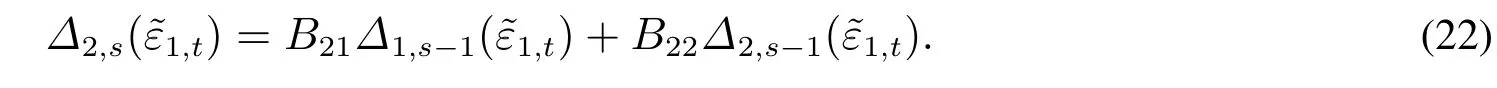
由上述推导过程,可以综合出基于VMA(1)模型的分位数脉冲响应函数一般表达式

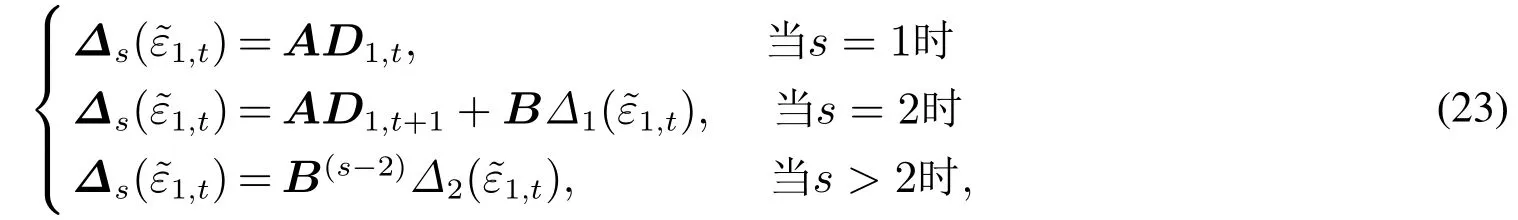
2)高阶情形

类似地,可以导出高阶向量移动平均VMA(k)模型的分位数脉冲响应函数一般表达式(以i=1为例)

当s=1时,同式(19),有分位数脉冲响应函数(QIRF)

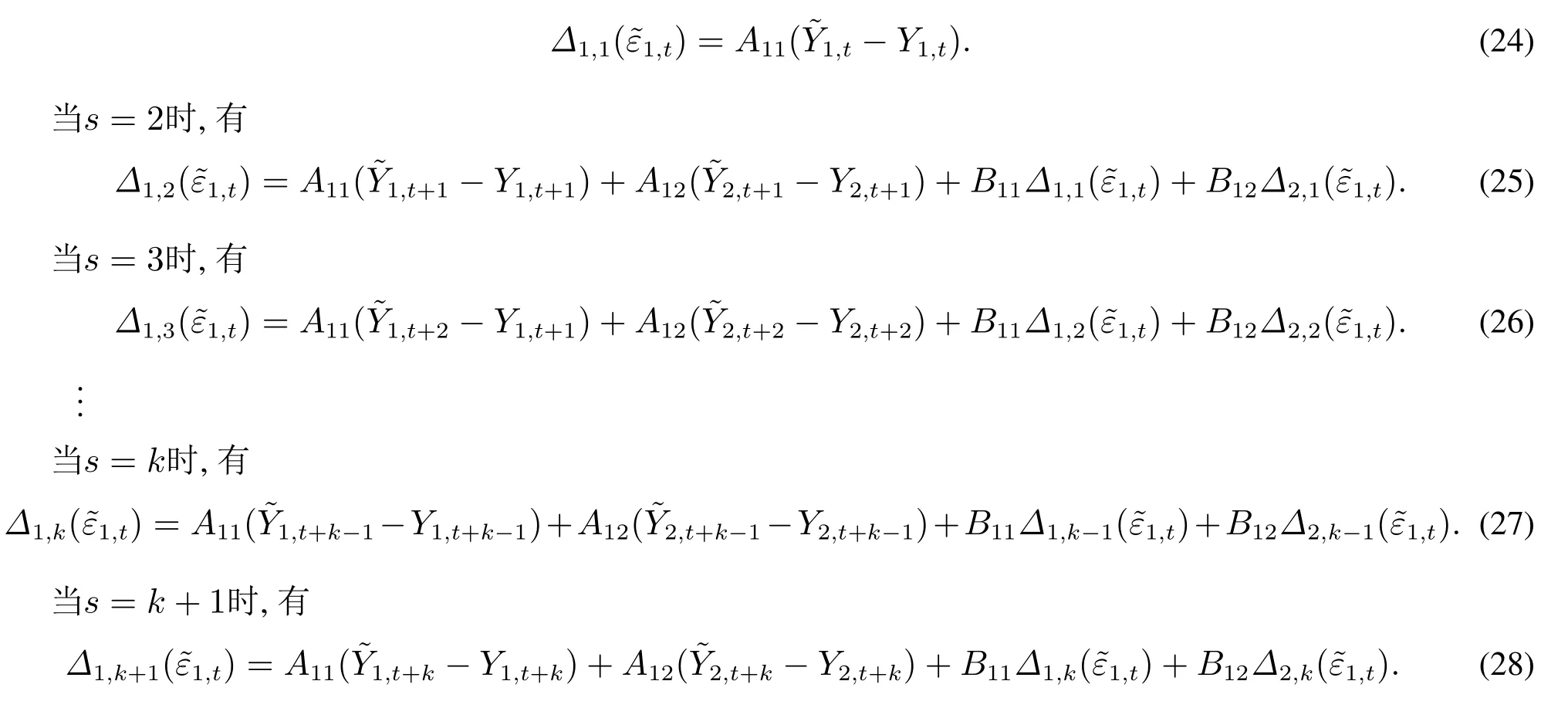
当s＞k+1时,由于VMA(k)的设置,无关,仅有对应的条件分位数与有关,即

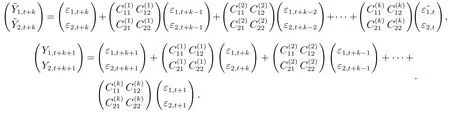
此时,有分位数脉冲响应函数

由上述推导过程,可以综合出VMA(k)模型的分位数脉冲响应函数一般表达式

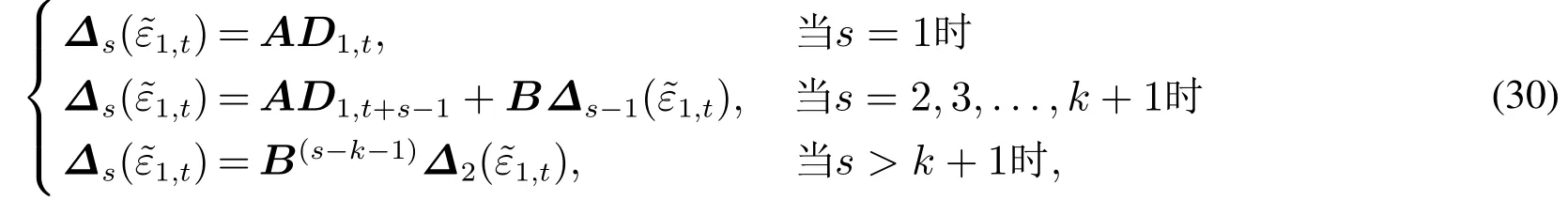
易见,基于VMA(1)模型得出分位数脉冲响应函数正是上式k=1时的特例.至此,本文讨论了更为一般情形下的分位数脉冲响应分析,运用高阶向量移动平均VMA(k)模型与QVARDL模型之间关系,推导出分位数脉冲相应函数.White等[19]的分位数脉冲响应分析是本文的特例形式,本文是其推广.

3.3 分位数脉冲响应函数分布特征

分位数脉冲响应函数也是随机变量,研究其分布特征对于把握其变动规律至关重要.给出如下引理.

引理1Hamilton[24]:对一个向量随机序列{Zt},若存在,同时有一函数g(·)其在c处有连续的一阶导数,则有.

由上述引理,可以得出下列结论.

定理3对于定义1中给出的脉冲响应函数,有

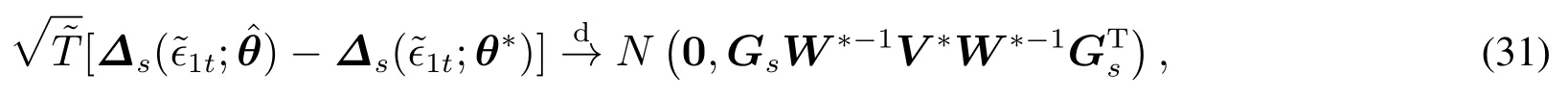
证明定理3的证明过程参见附录4.

4 实证研究

4.1 数据选择

杨博理等[25]的研究工作表明,向量自回归(VAR)模型能够有效地揭示金融市场之间动态关联关系.这里,使用本文提出的QVARDL(p,q)模型来检验美国次贷危机在世界范围的影响.在QVARDL模型(4)中,不考虑外生变量的影响,仅仅考虑内生变量滞后项的影响.以美国S&P500指数作为研究基准,同时选取如表1所示的14个不同国家(地区)的综合指数作为研究对象进行实证研究.样本数据取2005–01–01至2013–12–31 期间各市场指数日收盘价,其中以2005–01–01至2012–05–31为样本内,2012–06–01 至2013–12–31为样本外,样本数据均来自雅虎财经网站(http://finance.yahoo.com/).这一样本区间包含了2008年美国次贷危机的完整周期,便于定量研究美国次贷危险产生的影响.收益率采用对数收益率,用自然对数收盘价的一阶差分计算rt=100×(lnPt-lnPt-1).

4.2 参数估计

为考察美国次贷危机对其他国家(地区)带来的影响,以美国市场作为基础,与其他任意一个市场,分别建立二元QVARDL模型与VMA模型,共建立14个QVARDL模型与14个VMA模型.这里,使用VMA模型描述时间序列的动态变动规律,使用QVARDL模型描述时间序列条件分位数的变动规律.在估计VMA模型与QVARDL模型时,使用2.3节给出的AIC与BIC信息准则,确定了最优滞后阶数为VMA(2)与QVARDL(1,1).

表1报告了VMA(2)模型的参数估计结果,为进一步进行脉冲响应分析,定量揭示美国次贷危机冲击对于不同国家(地区)股票市场的影响,奠定了基础.表2报告了QVARDL(1,1)模型在一个分位点(τ=0.01,对应99%VaR)处的参数估计结果(限于篇幅,这里略去了其他分位点处的估计结果),可以得到几个初步结论.第一,在14个QVARDL(1,1)模型中,有超过一半的国家(地区)所得自回归系数矩阵B中的对角线元素(即B1(11)和B2(12))在统计上显著(10%水平),意味着条件分位数(与VaR风险对应)过程具有显著的自相关性.第二,QVARDL(1,1)模型中所有非对角线系数均显著不等于0,意味着美国与世界其他国家(地区)之间的金融风险存在相互影响.第三,值得注意的是,德国和巴西的自回归系数矩阵B各元素均在统计上显著(5%水平).作为欧洲经济的顶梁柱,德国的出口导向型经济增长模式以及稳定欧元区经济状况的能力在一定程度上对美国造成冲击;而作为新兴经济体的巴西,以与美国模式不同的经济政策不断加强与拉美邻国、非洲国家乃至印度和中国之间的政治经济合作,而这正是美国一再巩固“南北关系”的重要原因.第四,由于考虑到不同国家(地区)金融风险之间相互作用,QVARDL(1,1)模型能够更加准确预测其金融风险变化规律,结果见图1和图2.

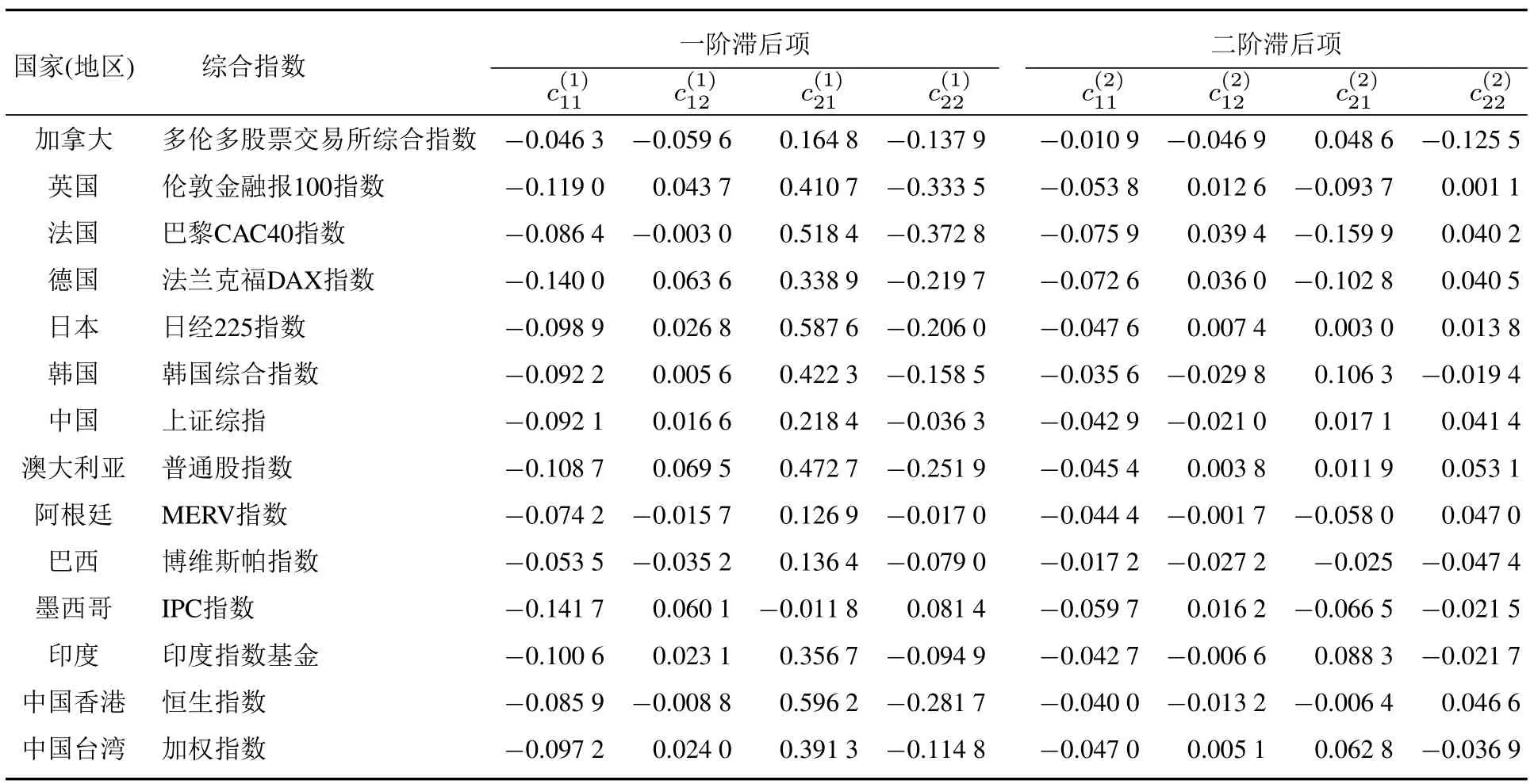
表1 14个国家(地区)股票指数与美国的VMA(2)模型估计结果Table 1 Estimated results of 14 countries(districts)from VMA(2)model

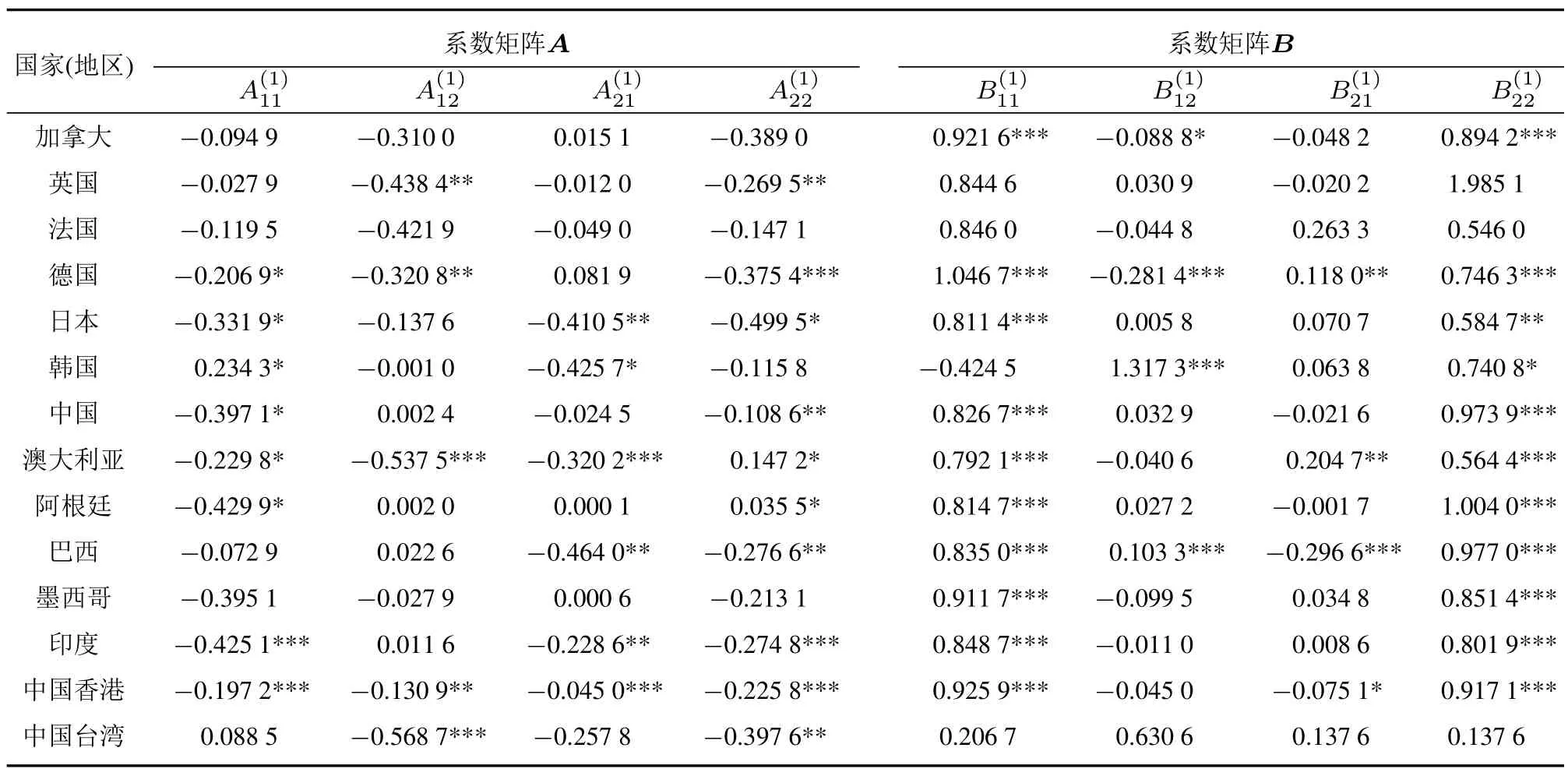
表2 14个国家(地区)股票指数与美国的QVARDL(1,1)模型估计结果(τ=0.01)Table 2 Estimated results of 14 countries(districts)from QVARDL(1,1)model with τ=0.01

图1给出了15个国家(地区)样本内的实际收益率(蓝线)与99%VaR估计结果(绿线)(限于篇幅,本文略去了其他置信水平VaR估计结果,只报告了极端风险值估计结果),图2则给出其样本外预测结果.在图1与图2中,美国的VaR是通过在QVARDL(1,1)模型中将两个内生变量都取做S&P500指数所得,其他国家(地区)的VaR是将模型中的两个内生变量分别取做S&P500指数及本国(地区)的市场指数.

由图1可以看出,第一,QVARDL(1,1)模型在样本内取得了很好拟合效果,表现为99%VaR变动趋势与收益率变化趋势吻合程度较高.第二,不同国家(地区)市场均在2007底至2008年初开始出现不同程度波动,并于2008年底至2009年初大幅度波动全面爆发,而这段时间恰逢美国次贷危机集中爆发并演变成全球性金融海啸.第三,在2011年中下旬不同国家(地区)再次出现不同程度波动,这可能源于欧元区主权债务危机影响.由图2可以看出,99%VaR同样与收益率变化趋势一致,表明QVARDL(1,1)模型同样具有很好的样本外表现.

综合图1和图2的信息可知,基于QVARDL(1,1)模型能够给出准确的VaR风险测度,具有很好的样本内与样本外表现.为精确检验模型的测算效果,本文采用Kupiec[26]无条件覆盖似然比(uc.LR)检验与Christoffersen等[27]条件覆盖似然比(cc.LR)检验对样本内与样本外VaR风险测度进行返回测试检验,同时还采用Engle等[14]提出的样本外动态分位数(DQ)检验作为指标检验方法,检验结果如表3所示.

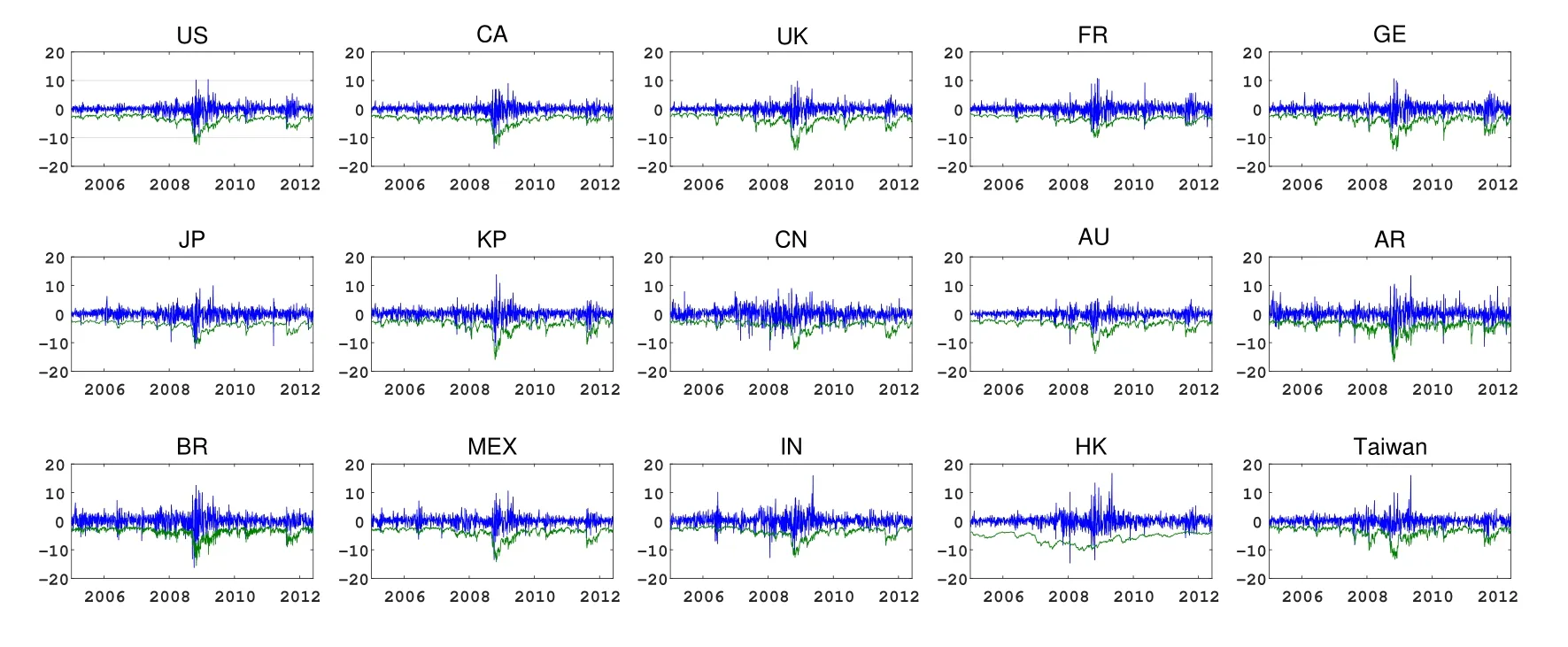
图1 15个国家(地区)股票指数的样本内99%VaR(τ=0.01)Fig.1 Stock indices returns plot for the in-sample days of 15 countries(districts)superimposed by VaR estimates at=1%and 5%

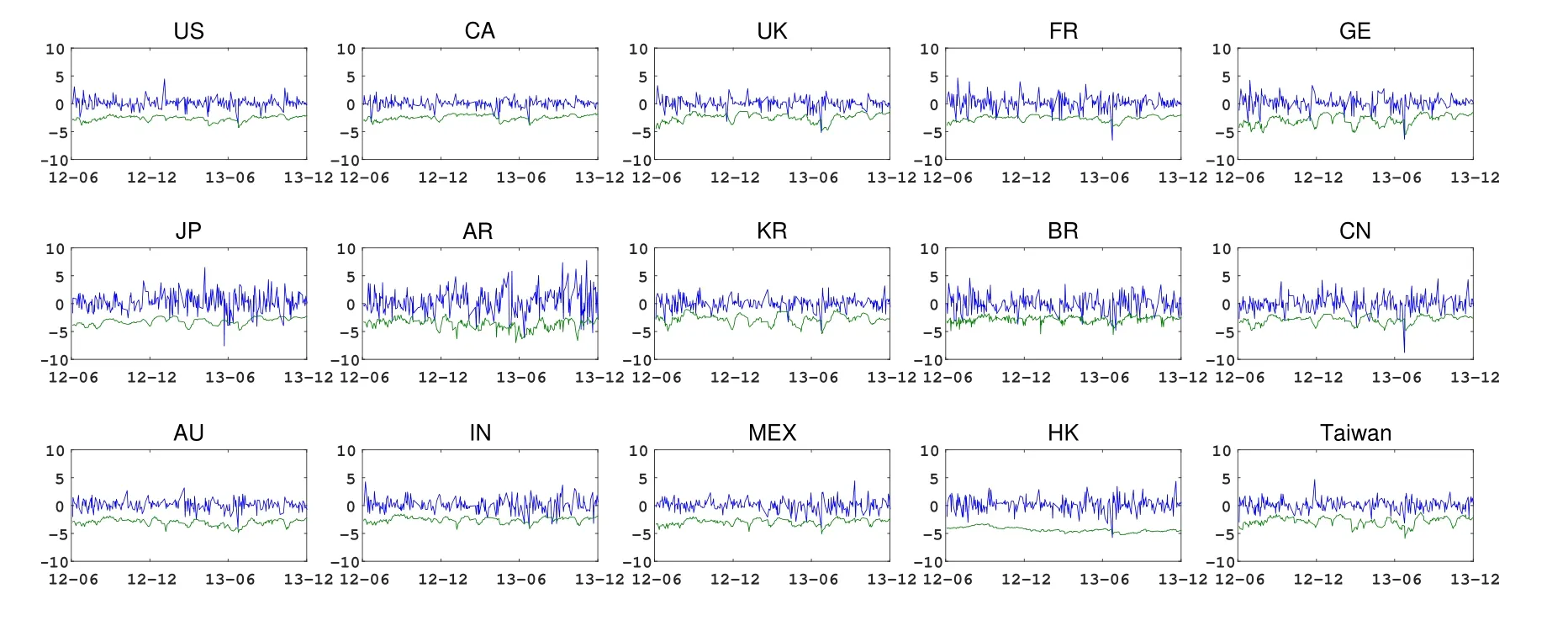
图2 15个国家(地区)股票指数的样本外99%VaR(τ=0.01)Fig.2 Stock indices returns plot for the out-of-sample days of 15 countries(districts)superimposed by VaR estimates at=1%and 5%

表3 99%VaR返回测试结果Table 3 Backtesting results of 99%VaR for 14 countries(districts)

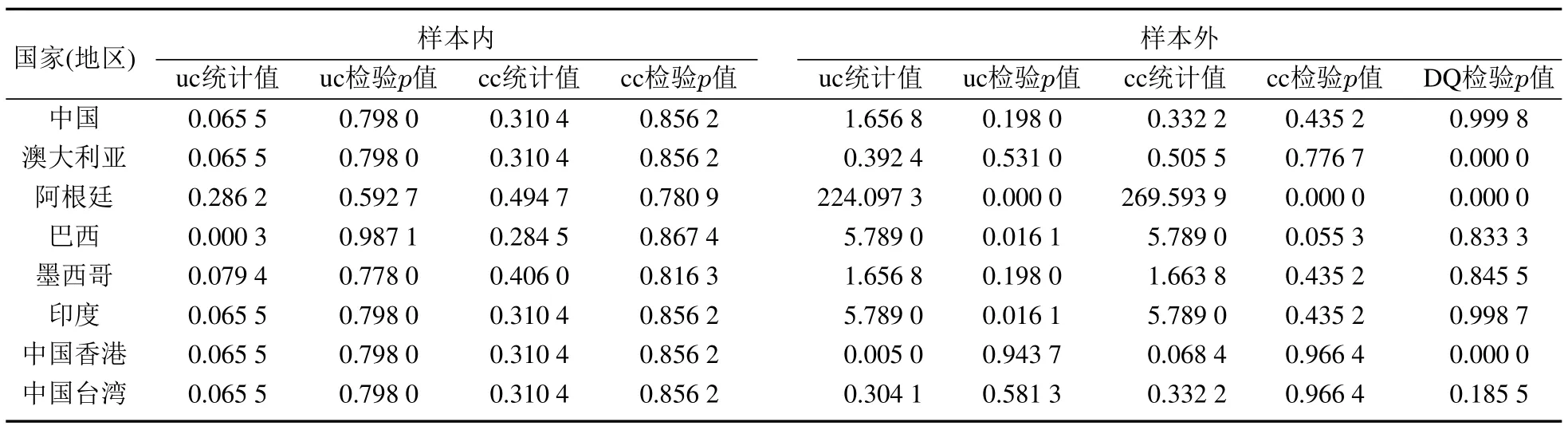
续表3Table 3 Continues

由表3,可以得到以下初步结果.第一,除美国以外的14个国家(地区)股票指数的VaR在样本内均有很好的拟合效果.其中,由uc.LR检验可以看出,QVARDL(1,1)模型对日本、韩国与巴西的拟合效果最优,表现为有较大的p值且都为0.987 1;由cc.LR检验则可以看出,QVARDL(1,1)模型对韩国与巴西拟合效果最优,表现为p值较大且都为0.867 4.第二,在14个股票指数VaR样本外预测中,有9个国家(地区)的股票指数通过了样本外DQ检验,仅有阿根廷MERV指数没有通过cc.LR检验;事实上,所有国家(地区)的股票指数均通过了uc.LR检验.这一实证结果也表明,在VaR返回测试中,uc.LR检验最为宽松,其次为cc.LR检验,最严格的为DQ检验.以上结果表明基于QVARDL(1,1)模型的VaR风险测度在样本内与样本外都取得了很好的效果,其中样本内更为有效,这也与预期结果相符.

4.3 分位数脉冲响应分析

由前面QVARDL(1,1)模型估计结果,已经判定美国金融市场与其他国家(地区)市场之间存在密切联系.本节主要通过分位数脉冲响应分析,定量揭示不同国家(地区)受美国次贷危机影响的程度与反应速度.黄友珀等[28]认为,有必要研究资产组合收益分位数预测问题.郭华等[29]通过脉冲相应分析考察由特定交易变量构成的脉冲交易对价格波动的冲击模式.本文中,在一个单位标准差冲击下的分位数脉冲响应函数可以直观地报告危机的传播过程以及危机被吸收(脉冲响应函数收敛于0)的时间,结果见图3.在图3中,横轴代表天数,纵轴表示99%VaR(对应0.01分位数)的变化.

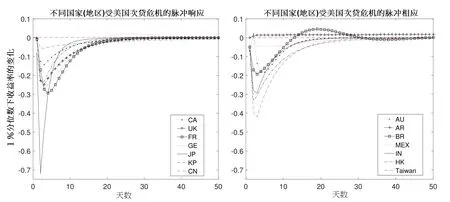
图3 14个国家(地区)受美国次贷危机影响的脉冲响应(τ=0.01)Fig.3 Impulse response of 14 countries(districts)to the U.S.subprime mortgage crisis(τ=0.01)

由图3,可以得到如下结果.第一,可以看出大部分国家(地区)在次贷危机爆发后2天∼3天内受到了严重的冲击,除了法国与澳大利亚约在5天左右才达到收益率的最低值.第二,欧洲地区包括法国、英国和德国,主要受到次贷危机对本地银行业的冲击,受到冲击后收益率百分比低至-0.2后都开始回升,并在约20天收敛于0值.第三,亚洲地区包括中国大陆、中国香港、中国台湾、韩国以及日本,其中中国大陆受到次贷危机冲击影响最小,脉冲响应过程也较短,可以看出美国次贷危机对于中国大陆的冲击有限,这可能是由于中国大陆准备金充足,所以并没有造成实质性的影响.中国台湾地区相对于中国香港地区受冲击更为严重,可能是中国台湾出口萎缩等原因导致了中国台湾地区经济衰退.亚洲其他地区,如日本与韩国对于次贷危机的响应却有着明显的差异.日本是受到次贷危机冲击最大的国家,收益率百分比一度跌破-0.65,这种现象与日本近年经济发展不稳定有密切的关系,在此期间日本需要面对经济衰退和通货膨胀的双重压力.第四,墨西哥与阿根廷几乎没有受到次贷危机的冲击,作为拉丁美洲的新兴市场,受益于长期以来实施的对外贸易自由化政策,对美国商品市场的依赖性较小,因而受美国次贷危机的冲击相对有限.

5 结束语

本文提出了一个新的分位数回归模型:分位数向量自回归分布滞后(QVARDL),给出其数学表示、参数估计、滞后阶数选择、脉冲响应分析等一整套建模方法.该模型可以同时刻画多个时间序列在多个分位点处条件分位数之间的关联关系,能够整体提升分位数回归的功能.在结构分析方面,主要通过回归系数矩阵,定量揭示不同时间序列及其分位数之间的相互依赖关系,有助于解释经济系统内部联系与相互影响.在经济预测方面,主要通过多变量与自回归,从横向与纵向两个方面把握条件分位数的变动规律,有助于准确预测响应变量在不同分位点处的条件分位数,进而可以准确地进行风险评估.在政策评价方面,主要通过分位数脉冲响应分析,可以考察对经济系统实施一个冲击,定量刻画经济系统内部的响应情况,评估经济政策的有效性.

为检验提出模型与方法的有效性,本文将其应用于解释美国次贷危机对世界范围金融市场产生的影响.实证中,选取世界范围内主要国家(地区)资本市场作为研究对象,建立QVARDL(p,q)模型并进行分位数脉冲响应分析.通过QVARDL(p,q)模型估计结果发现,一方面,绝大多数国家(地区)的金融风险具有显著的自相关性;另一方面,美国对世界其他国家(地区)的金融市场存在显著影响.通过脉冲响应分析发现,美国次贷危机对不同国家(地区)的资本市场在影响程度、影响方式、响应时期等方面有着不同的表现.本文的研究方法与实证结果,为从新的角度研究金融风险及其传染性提供了一个参考.