基于Credit期权的集群式供应链采购模型及算法分析
2014-04-10刘春玲肖位春黎继子曹晓刚黄纯辉
刘春玲,肖位春,黎继子,曹晓刚,黄纯辉
(1.武汉纺织大学供应链系统研究中心,湖北 武汉 430073;2.华中科技大学管理学院,湖北 武汉 430070)
1 引言
集群式供应链是以产业集群为运作平台的供应链系统。在产业集群内,大量企业围绕着同一类产品进行生产,形成了完备的上下游企业配套体系以及供应链网络[1]。由于产业集群内中小企业占据比例较大,同时这些中小企业在协作过程中,呈现出“抱团性”、“社会网络性”和“根植性”。因此集群式供应链在协作模式上,具有与大企业不一样的供应链合作方式,特别是在供应链采购上,更多体现出基于血缘、人缘、地缘和亲缘的信任采购,即是一种非正式契约的Credit期权的采购协作模式,同时由于产业集群内中小企业制造品类的同一性,使得在供应链采购上具有联合规模优势。事实上也是如此,在中山沙溪休闲装产业集群中,休闲装生产企业如雷柏高、汉弗莱和剑龙等企业,为了降低成本,就联合起来进行集中式采购。
关于采购问题的研究,目前国内外文献主要体现在分散式采购和联合采购两个方面,换言之,也就是体现在独立决策与集中决策两种形式。其中Lau[2]发现单供应商-单采购商在独立采购中不同需求曲线的效用;Heydari和Chaharsooghi[3]和盛方正和季建华[4]建立了单供应商-单采购商对订货量和再订货点的决策模型;Tiwari[5]为了确保较高服务水平,提出了单供应商-单采购商的多交通运输工具选择模型;在此基础上,更多文献则是对单供应商-多采购商或多供应商-单采购商采购模式的研究,Weng[6]将数量折扣下采购模型扩展到了单供应商-多采购商模型中;Chu和Leon[7]则考虑在各参与者信息对称和不对称的情形下,研究单供应商-多采购商的采购问题;Abdul[8];李建斌和杨瑞娜[9]建立了在单供应商-多采购商采购中的多级库存系统。而Sinha和Sarma[10]分析了市场随机需求时,单供应商-多采购商订货批量的决策。更进一步,Sarker和Diponegoro[11]在多约束条件下,考虑了仓库和运输成本因素的多供应商-多采购商(MV—MB)采购模型;Taleizadeh等[12]则分析了随机需求和采购提前期随机下的多供应商-多采购商的采购模型。在联合采购上,Chan等[13]将单供应商-多采购商分散式决策扩展到了集中式决策来优化采购;Hoque[14]为单供应商-多采购商联合采购建立了仓储模型,并考虑订货提前期、运输批量等现实约束条件对采购商库存成本的影响。Moon,Cha,Lee[15]将能容纳不同货物的第三方仓库引入到了需求导向的联合采购中;Lu Liang和Qi Xiangtong[16]就联合采购中,多产品动态成批排列进行研究,分析不同成批策略对采购成本的影响程度。所需说明的是,这些联合采购多为NP-HARD问题,不少学者也对相关算法进行了探讨,如Moon和Chab[17]对联合采购及算法(C-RAND算法、GA算法、GOYAL等算法)进行一一分析。
总之,以上文献分析都是基于采购商在采购货物运达后立即支付全额费用来进行研究,但是这种情况在实际中发生比例较小,通常做法都是采购商延期支付货款。虽然Rachamadugu[18]分析了经济订货批量和延迟支付周期长度的关系;Kim等[19]则基于弹性需求方程基础上提出了单供应商-单采购商的供应链模型,通过最优延迟周期来最大化供应商的利益。Jamal[20]则扩张了这个模型,考虑到在最大延迟周期内的最优延迟周期。但针对于中小企业特点的延迟支付以及基于多供应商和多采购商(MV-MB)集群式供应链联合采购目前研究极少。基于此,本文引入了柔性周期和基于Credit期权策略,来建立集群式供应链MV-MB联合采购模型,并对模型设计了相应的Enumeration算法进行求解和分析。
2 集群式供应链分散式采购模型
在产业集群中,存在围绕同一产业的诸多上游供应商j和下游采购商i,假设Qj为集群内供应商j的生产批量;Pj为供应商j的生产速率;Fj为供应商j的固定生产费用;Cij为供应商j对采购商i的供货处理费用;Hj为供应商j的仓储费用;ρD为采购量为D时运费折扣率;G为运输能力限制;Hij为采购商i对供应商j的单位仓储成本;Qij为采购商i对供应商j的产品订货量;Tij为采购商i对供应商j的采购周期;Dij为采购商i对供应商j的产品年采购量;Sij为采购商i对供应商j的订货处理费用;wij为采购商i对供应商j的产品单位运输成本;mi为采购商的库存能力限制;kij为联合采购时集群内采购商采购周期为最小采购周期的kij倍(正整数,决策变量);Nj为联合采购时集群内供应商生产周期为最小采购周期的Nj倍(正整数,决策变量);另外,文中出现的p表示采购商,s表示供应商。上标d表示独立决策、c表示集群式供应链联合决策、*表示最优。
2.1 基本采购模型
首先考虑最基本的单一采购商向单一供应商采购的情况,设定采购商采购量已知且固定,并且供应商不允许缺货发生,单一采购商i向单一供应商j采购,单位时间总采购成本为:
(1)

(2)
将(2)式代入(1)式化简,得到采购商i分散式决策下最优采购总成本为:
(3)
由于供应链中采购商i进行分散式决策且采购周期不确定,所以供应商j必须有一个安全库存Qij*来满足采购商i的需求从而保证不缺货。因此,供应商j单位时间总成本为:
(4)

(5)
将(2)、(5)式代入(4)式得到供应商j的总成本为:
(6)
2.3 基于MV-MB集群式供应链分散式采购模型
集群式供应链中,中小企业生产产品类似性使得集群式供应链系统中同一链节处存在多个采购商,并且向共同的多供应商进行采购,在这个多供应商-多采购商采购系统中,各供应商相互独立,所以由单供应商-单采购商系统成本函数可以很简单地扩展到多供应商-多采购商成本函数:
(7)
分散式决策采购模式下,集群式供应链系统中各参与方均已自身利润最大化为出发点来进行独立的分散式决策。然而,由于缺乏信息共享导致信息不对称很容易产生双边效应,且各自最优决策都有可能影响其他参与者利润,从而使得供应链能效低下。显然,集群式供应链中,供应商与采购商联合起来进行集中式决策十分必要。
3 基于Credit期权的集群式供应链联合采购模型
3.1 柔性周期采购模型
Banerjee和Burton[21]指出在联合采购中,供应商为了降低自身供货处理次数与安全库存,会迫使所有采购商采用一个共同的采购周期T。然而,让所有的采购商都采用固定的采购周期虽然能降低供应商缺货的可能却并不合理,低需求的采购商倾向更短的采购周期,而对需求量大的采购商而言,较长的采购周期更有利。由Chan和Kingsman[22]提出来的柔性联合采购周期策略可以很好的解决上述问题。在柔性联合采购周期策略中,假定一个基本采购周期T作为所有采购商最短的采购周期,联合采购中集群式供应链的任何采购商均可以选择基本采购周期的ki(ki为正整数)倍作为其独立的采购周期。而供应商也可以选择选择基本采购周期的N倍(N为正整数)作为生产周期,且必须满足N≥ki。由以上分析可知,在集群式供应链柔性周期采购模型中,采购商采购周期为kijT,供应商生产周期为NT,因此(1)式可整理为:
(8)
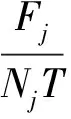
(9)
由以上分析可知基于柔性周期的集群式供应链MV-MB联合采购系统总成本为:
(10)
3.2 Credit期权联合采购模型
(11)
由以上可知,供应商j为了刺激采购商加入联合采购中,必须弥补其增加的采购成本。而已有关于联合采购文献中,都假设采购商在采购货物运达后立即支付全额费用,但是这种情况在实际中可能性比较小。为此,本文考虑到资金时间价值,引入Credit期权,考虑延迟支付周期,使得供应商j能促成集群供应链系统进行联合采购。
为了吸引集群内采购商加入到联合采购中,供应商需要用资金时间价值也就是延迟支付策略来弥补采购商增加的采购成本(11)式。然而,对于供应商而言,过长的延迟支付时间也会相应增加自身资金时间成本,过短的延迟支付时间无法刺激采购商加入联合采购中。因此,合理确定延迟支付时间对于供需双方能否达成联合采购十分必要。为了刺激集群内采购商进行联合采购,供应商j可以提供给采购商i一个延迟支付时间Mij,来弥补增加的采购成本。
Sarmah等[23]指出,采购商资金时间价值可以表示为:DijHijtij,其中tij表示延迟支付时间,因此由(11)式可知供应商必须向采购商提供的延迟支付时间为:
(12)

图1 联合采购下采购商库存状态
采购商按照有Credit期权的联合采购模式向供应商订货,图1表示集群式供应链联合采购模式下采购商库存状态,大三角形区域表示采购商联合采购库存成本,小三角形表示独立采购下采购商库存成本,虚线梯形区域表示采购商增加的成本,需要供应商提供延迟支付来弥补。采用Credit期权联合采购策略,虽然采购商成本会增加(大三角形面积大于小三角形区域面积),但是由于有采购商提供的延迟支付弥补(虚线梯形区域),采购商的成本会降低到独立采购下最优成本。
对于供应商j而言,为了刺激采购商联合采购而提供延迟支付时间Mij的同时会增加自身资金时间成本:
(13)
注意到,供应商j需要需要知道的关于采购商i独立采购时的最优采购周期Tij*可以从历史订货记录里面得到。因此供应商可以准确的为采购商提供延迟支付时间,不至于过高或过低的提供延迟支付时间而产生双边效应。
通过延迟支付的补偿,每个采购商都不会因为采购成本增加而拒绝加入Credit期权联合采购。供应商由于提供延迟支付增加的成本为(13)式减去运费折扣:
(14)
因此得到集群式供应链供应商的总成本函数:
(15)
由以上分析可知,采购商总采购成本由于延迟支付的补偿没有发生任何变化,供应商的成本却有所变化。因此本文目标函数为追求供应商总成本最低,从而联合采购系统总成本最低。由此得到基于Credit期权集群式供应链系统目标函数为:
整理得到:
(16)
s.t.
(17)
(18)
(19)
ρ=f(D)
(20)
其中,式(17)为采购商库存能力限制,式(18)为运输能力限制,式(19)为供应商生产能力限制,式(20)为运费折扣条件限制,表示运输折扣率与运输批量成某种函数关系。
4 模型Enumeration算法
在基于Credit期权下的集群式供应链采购模型中,由于集群内供应商的弥补使得每个采购商的采购成本与其在独立采购下一致,因此本文优化目标为供应商成本最小,从而该集群式供应链采购系统成本最低。目标模型式(16)为关于Nj和kij二元函数,且Nj和kij均为小于等于365(假设一年为365天,T=1/365)的正整数,因此本文设计出相应的Enumeration算法来找到最优解,也就是在确定的Nj值下寻找最优的kij值。对于给定的Nj值,目标模型式(16)是关于kij的一元函数,将其简写为:
(21)
其中,
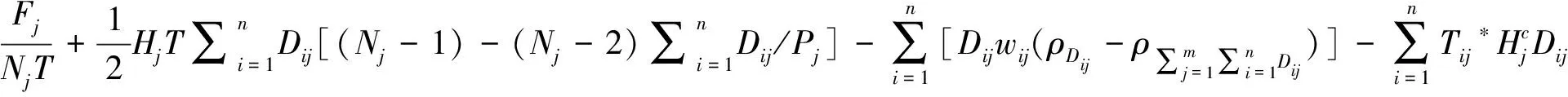
(22)
(23)
(24)
求式(20)关于kij的一阶导数,得到:

Step 1.设T=1/365,i=1,j=1,Nj=1。
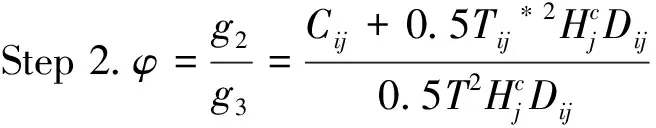
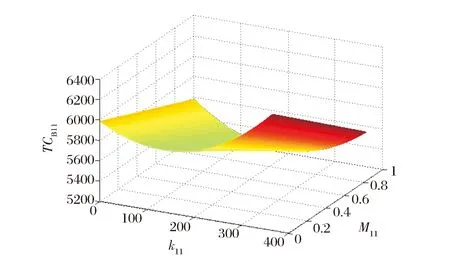
Step 5.如果i Step 7.如果Nj<365,设Nj=Nj+1,进入Step 2。 Step 8.找到最优解MinTCsj(Nj,k1j,k2j,…,knj)。 Step 9.如果j Step 10.找到最优解(N1、N2,…,Nj,k11、k12,…,k1j,…,knm)使得目标函数: 为了比较集群式供应链系统中独立采购与基于Credit期权的联合采购两种策略下供应商、采购商以及整个集群式供应链系统采购成本差异。假设集群式供应链系统中有三个相对独立的供应商、两个采购商。相关模型参数如表1所示。采购商1和采购商2的库存能力限制为m1=m2=1500;运输能力限制为G=5000;单位运费折扣限制为ρMax=1,ρMin=0.8,ρD=1.23-2.85×10-5D,折扣运量下限为D=8000,运量上限为D=15000。 表1 模型相关参数值 表2 采购成本信息 由相关参数及模型可计算出供应商、采购商以及整个集群式供应链系统在分散式采购和基于Credit期权的联合采购策略下的相关成本如表2所示。 由表2可知,在集群式供应链系统独立采购的情况下,采购商1向供应商1、2、3的经济采购周期分别为103天、37天、35天,采购成本分别为7259.58、10275、00、11952.11,总采购成本为29486.69;采购商2向供应商1、2、3的经济采购周期分别为86天、66天、42天,采购成本分别为8382.31、7568.13、11292.85,总采购成本为27243.29;供应商1、2、3成本分别为24007.23、20654.90、18112.10,总共为62774.23。而在基于柔性周期的Credit期权联合采购策略中,采购商1向供应商1、2、3的经济采购周期分别为72天、36天、24天,供应商1、2、3分别向采购商1提供36、18、12天的延迟支付时间,采购成本由于供应商提供的延迟支付时间弥补保持不变,仍然分别为7259.58、10275、00、11952.11;采购商2向供应商1、2、3的经济采购周期分别为72天、24天、24天,供应商1、2、3分别向采购商2提供36、12、12天的延迟支付时间,采购成本由于供应商提供的延迟支付时间弥补仍然分别为8382.31、7568.13、11292.85。供应商1、2、3成本分别降低到为22519.31、18751.06、17532.36,总共为58802.73,分别降低了6.2%、9.2%、3.2%。分散式采购下集群式供应链系统总成本为采购商1、2与供应商1、2、3成本之和,即为119504.21,基于柔性周期的Credit期权联合采购策略下系统总成本为115532.71,降低了3.3%。显然对于整个集群式供应链系统来讲,采用基于Credit期权的联合采购策略既能维系合作关系,又能为降低该系统的总成本,为该集群企业提升竞争力创造条件。 同时也不难发现,系统节约的成本主要是由于供应商与采购商协调后,降低了系统双边效应,供应商能确定各采购商的采购周期与采购批量,从而减少安全库存降低库存成本,以及采用联合采购以后由于数量优势而获得的运费折扣。 (1) 延迟支付时间敏感性分析 为了研究集群内采购商的采购周期与库存成本对供应商所能提供的延迟支付时间的影响,以采购商1向供应商1进行采购为研究对象,采购商采购周期波动范围为[1,365],库存成本波动范围为[0,100]。如图2所示,当采购商采购周期和库存成本都很小时,供应商为了吸引采购商加入到联合采购中,使其改变其较短的独立采购周期到较长的联合采购周期,需要提供很长的延迟时间来进行激励,由图可以看出,M11需要大于1年,在这种情况下,供应商不适合组织采购商进行联合采购;在采购商采购周期不变的情况下,供应商提供的延迟支付时间随着采购商库存成本的增加而降低,因为采购商库存成本较高时,供应商只需稍微提供一个延迟支付时间,采购商都能大幅度降低成本,但当库存成本上升到一定水平后延迟支付时间基本维持稳定,因为此时采购商的联合采购成本由于延迟支付的弥补已经等于独立决策时的最优成本;在采购商库存成本不变的情况下,供应商提供的延迟支付时间随着采购商采购周期增加先降低再升高,这是因为采购商在联合采购下的采购周期越往独立决策最优采购周期靠拢,供应商需要提供的刺激也就是延迟支付时间就越小。 图2 延迟支付时间敏感性程度 图3 采购商成本敏感性程度 (2)采购商成本敏感性分析 选取采购商1向供应商1进行采购为研究对象来分析延迟支付时间与联合采购周期对采购商成本的影响,延迟支付时间波动区间为[0,1],联合采购周期波动范围为[1,365]。在不同的延迟时间与采购周期下,采购商成本波动趋势如图3所示。由图3可知,在延迟支付时间一定的情况下,采购商的成本随着联合采购周期的增加呈先增后减的趋势,这是由于过低的采购周期意味着采购次数过高,相应的采购固定成本增加,而过高的采购周期也将使库存成本大幅度升高;而在联合采购周期确定的情况下,采购商的成本在达到供应商与采购商协调的延迟支付时间之前急剧下降,但超过了该延迟支付时间后,由于延迟支付时间完全弥补了采购商的库存机会成本,使得采购商联合采购成本下降缓慢甚至维持不变,这将有助于采购商与供应商在联合采购模式下协商延迟支付时间。 集群式供应链是以产业集群为运作平台的供应链系统。文首先在单供应商-单采购商采购模型的基础上,建立了多供应商-多采购商的集群式供应链分散式采购模型。在模型中通过采用柔性周期和Credit期权模式,构建了适合多频次、小批量、柔性、信任等特征的基于Credit期权的集群式供应链MV-MB联合采购模型,并设计出针对模型的Enumeration算法。通过分析发现在基于Credit期权的联合采购策略下,各采购商虽然改变了经济采购周期与采购批量,但由于有延迟支付的弥补,采购成本不会上升。对于供应商而言,虽然为采购商提供了一定的延迟支付时间增加了自身资金时间成本,但通过与采购商协商,降低了系统双边效应,供应商因此能确定各采购商的采购周期与采购批量,从而减少安全库存降低库存成本,同时由于联合采购数量优势而获得的运费折扣,使得各供应商成本都有明显下降,从而整个集群式供应链系统成本降低。通过算例分析证明了模型的有效性。 但本文所提出的解决方法也存在一定不足,如只考虑到了采购商在固定需求下的联合采购问题等,而现实中市场需求往往是随机不固定的,今后关于联合采购的研究可以从这些方面展开。 参考文献: [1] Li Jizi, Xiong Naixue, Park J H.Intelligent model design of cluster supply chain with horizontal cooperation[J].Journal of Intelligent Manufacturing, 2009,11(8): 256—268. [2] Lau A, Lau H S.Effects of a demand-curve's shape on the optimal solutions of a multi echelon inventory pricing model[J].European Journal of Operational Research, 2002,147(3): 530-548. [3] Chaharsooghi S K, Heydari J.Supply chain coordination for the joint determination of order quantity and reorder point using credit option[J].European Journal of Operational Research, 2010,204(1): 86-95. [4] 盛方正,季建华.最优期权合同组合的充要条件及采购方法[J].系统管理学报,2008,(17)3:307-311. [5] Tiwari M K, Raghavendra N, Goyal S K.A hybrid Taguchi-Immune approach to optimize an integrated supply chain design problem with multiple shipping[J].European Journal of Operational Research, 2010,203(1): 95-106. [6] Weng Z K.Modeling quantity discounts under general price-sensitive demand functions: optimal policies and relationships[J].European Journal of Operational Research, 1995,86(2): 300-314. [7] Chu C L, Leon V J.Single-vendor multi-buyer inventory coordination under private information[J].European Journal of Operational Research, 2008,191(2): 485-503. [8] Abdul J B, Gutierrez J, Sicilia M J.Policies for a single-vendor multi-buyer system with finite production rate[J].Decision Support Systems, 2008(1),46: 84-100. [9] 李建斌,杨瑞娜.现货价格和需求关联时期权组合合约模式下采购风险管理策略[J].中国管理科学,2011,19(1):12-20. [10] Sinha S, Sarma S P.Single-vendor multi-buyer discount pricing model under stochastic demand environment[J].Computers&Industrial Engineering, 2010,59(4): 945-953. [11] Sarker B R, Diponegoro A.Optimal production plans and shipment schedules in a supply-chain system with multiple suppliers and multiple buyers[J].European Journal of Operational Research, 2009,194(3): 753-773. [12] Taleizadeh A A, Akhavan S T, Barzinpour F.Multiple-buyer multiple-vendor multi-product multi-constraint supply chain problem with stochastic demand and variable lead-time: A harmony search algorithm[J].Applied Mathematics and Computation, 2011,217(22): 9234-9253. [13] Chan C K, Lee Y C E, Goyal S K.A delayed payment method in coordinating a single-vendor multi-buyer supply chain[J].European Journal of Operational Research, 2010,127(1): 95-102. [14] Hoque M A.An optimal solution technique to the single-vendor multi-buyer integrated inventory supply chain by incorporating some realistic factors[J].European Journal of Operational research, 2011,215(1): 80-88. [15] Moon I K, Cha B C, Lee CU.The joint replenishment and freight consolidation of a warehouse in a supply chain[J].International Journal of production Economics,2011,133(1):344-350. [16] Lu Liang, Qi Xiangtong.Dynamic lot sizing for multiple products with a new joint replenishment model[J].European Journal of Operational Research,2011,212(1):74-80. [17] Moon I K, Chab B C.The joint replenishment problem with resource restriction[J].European Journal of Operational Research, 2006,173: 190-198. [18] Rachamadugu R.Effect of delayed payments on order quantities[J].The Journal of Operational Research, 1989,40: 805-813. [19] Kim J, Hwang H, Shinn S.An optimal credit policy to increase supplier's profits with price-dependent demand function[J].Production Planning and Control, 1995,6(1): 45-50. [20] Jamal A M M, Sarker B R, Wang Shaojun.Optimal payment time for a retailer under permitted delay of payment by the wholesaler[J].International Journal of Production Economics, 2000,66(1): 59-66. [21] Banerjee A,Burton J S.Coordination vs.independent inventory replenishment policies for a vendor and multiple buyers[J].International Journal of Production Economics,1994,35(1):215-222. [22] Chan C K, Kingsman B G.Co-ordination in a single-vendor multi-buyer supply chain by synchronizing delivery and production cycless[J].Transportation research, 2007,43(6): 90-111. [23] Sarmah S P, Acharya D, Goyal S K.Coordination of a single-manufacture multi-buyer supply chain with credit option[J].International Journal of Production Economics, 2008,111: 676-685.
5 算例分析
5.1 数值分析
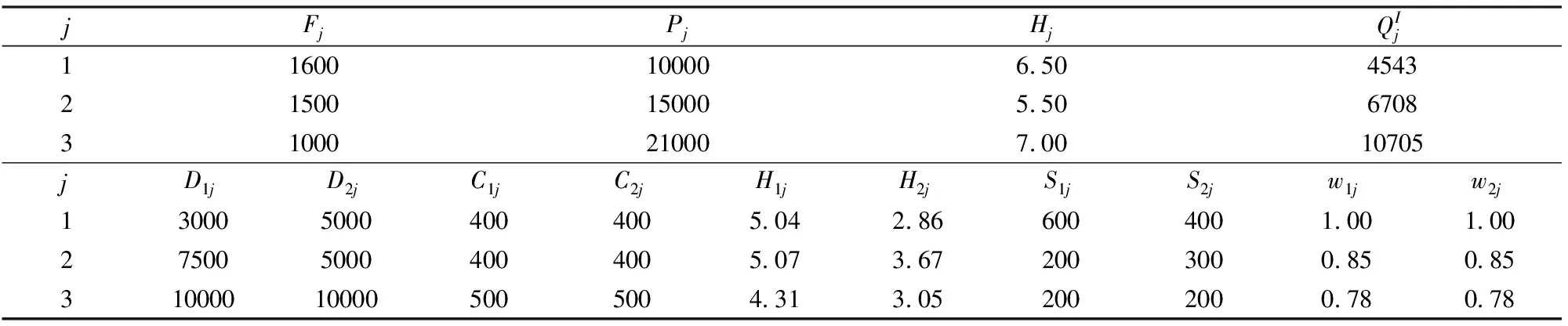

5.2 敏感性分析

6 结语
