稀疏角度CT图像重建算法研究

2018-10-24林泽田

计算机应用与软件 2018年10期

林泽田王单

1(北京航空航天大学数学与系统科学学院北京 100191)2(北京航空航天大学经济管理学院北京 100191)

0 引言

计算机断层成像CT(Computed Tomography)技术是指利用X射线穿透物体的衰减信息进行重建来获得物体的断层图像信息的技术，该技术被公认为20世纪后期最伟大的科技成果之一[1]。在医学诊断领域，CT技术已在医学成像领域确立了其不可动摇的地位。不仅如此，在工业无损检测、树木年轮测定、地球资源勘探等领域，CT技术也成为了有力的手段。然而，在实际的应用过程中，由于受辐射剂量、对比度等的约束，抑或是受现实条件限制，只能采集到部分数据。而在不完全数据的CT图像重建中，大多涉及到稀疏角度图像重建。基于此背景，本文展开研究。

2006年，文献[2]提出了压缩感知理论。该理论基于已知信号具有稀疏性或可压缩性，对信号数据进行采集、编码以及解码。当信号具有稀疏性或可压缩性时，该理论表明通过采集少量的信号投影值便可以实现信号的准确性或者近似重建。该理论突破了传统采样定理的局限，实现了压缩和采样的统一，在信息与信号处理方面带来革命性的突破，并已成功应用在人脸识别、地震勘探、通信与信号处理等诸多领域。

信号重构算法是一种由投影矩阵以及投影测量值重建出来原始信号，一般把问题转化为求解l0范数的优化问题。目前为止，典型的重建算法有贪婪算法[3]、l1最小化算法以及全变差TV(Total Variation)最小化算法[4]。自从2006年，文献[2]提出压缩感知理论，发现l1最小化与l0最小化的等价之后，在如安检、核磁共振等方面，压缩感知和l1最小化算法已经被广泛应用。进而，对于图像重建问题而言，文献[5]研究表明应用全变差最小化算法能够更好地保留图像的边界，而这对于特征图像很重要。全变差最小化算法的优点来自一个很重要的性质，那就是它能够恢复非稀疏的但具有分片连续性质的图像。换言之，全变差正则化能够成功地应用于具有梯度稀疏的信号或图像。近些年，变量分离思想也为解决全变差最小化问题提供了新的有效解决途径，这强力推动了单像素相机等硬件的发展。

近几年，诸多学者在研究CT图像重建的稀疏表示模型的过程中，取得了一些重要研究成果。比较普遍的做法就是首先建立合适的目标函数，之后寻找求解目标函数的快速算法。文献[6]的目标函数是最小化基于压缩感知的全变差正则化，基于全变差最速下降法和凸集投影约束，提出二者相结合的ASD-POCS算法。陈庆贵等人又基于总变差最小化原则，提出了PICS算法。文献[7]改进了目标函数，在全变差正则化目标函数中加入约束条件重建出的先验图像，用引用参数平衡两个目标函数的权重，之后采用迭代重建算法和最速下降法进行模型求解，提出了先验约束压缩感知PICCS(Prior Image Constrained Compressed Sensing)算法。文献[8]又基于总变差最小化原则，提出了PICS算法。这些算法虽然对图像的整体信息有较好的恢复，但是仍然存在一些伪影。

Bregman迭代正则化最早由文献[9]引入图像处理领域，该算法主要分为线性Bregman算法和分离Bregman算法两种，后来被广泛应用于基于压缩感知的核磁共振成像和基于小波变换的图像去噪中。文献[10]将分离Bregman算法用于全变差正则化图像重建，分析了算法可行性，得到了更快的收敛速度。文献[11]将分离Bregman算法与先验图像相结合，也取得了很好的效果。

近年来有学者采用增广Lagrangian方法进行研究，该方法应用了加入先验信息等思想。文献[12]提出了有序线性增广Lagrangian(OS-LALM)算法，模型的目标函数为全变差正则化。实验显示，有序线性增广Lagrangian算法能够有效加速CT图像重建的收敛速度，同时，当子集个数较多时，能有效减少伪影。但该算法需要首先对系统矩阵进行选择排序，这大大降低了效率。之后又提出了改进过的松弛的有序线性增广拉格朗日算法。但是，这些算法或者降低了重建效率，或者存在小范围的伪影。

为了提升CT图像重建的质量效率，本文提出外点惩罚函数增广Lagrangian EPFALM算法。首先，提出了新的稀疏角度CT图像重建的目标函数并求解；然后，通过仿真实验，将所提出的算法与前人算法作对比，验证了EPFALM算法用于稀疏CT图像重建时的质量和效率优势。

1 CT图像典型算法综述

滤波反投影FBP算法尽管已提出多年，目前依然是广泛应用的图像算法之一。其重建算法原理为先对各个视角θ的投影数据进行滤波，然后反投影，累加计算f(x,y)。该算法虽然计算效率高，重建速度快，但对数据完整性要求很高。

代数重建ART算法由Kaczmarz提出，由Gordon等人用于图像重建领域。Hounsfield的第一台CT机实际上用的是ART算法。该重建算法原理是给定重建区域初值，将所得投影值残差沿射线方向反投影从而对图像进行校正，进而满足要求、结束迭代。该算法较适用于数据不完全的情况，但对较大图像重建速度较慢。

分离 Bregman算法由文献[13]提出，并被文献[14]用于CT图像重建。分离 Bregman算法是解决l1范数目标函数最小化的有效算法，已被广泛应用与图像处理的各个领域。该算法相对于传统的算法，能够较好地抑制由于数据不足带来的条状伪影，但是收敛速度较慢，重建时间较长。

本文提出一种新的稀疏角度CT图像重建算法，即EPFALM算法。该重建算法的原理是采用增广Lagrangian 罚函数方法，先将约束问题非约束化，再通过在交替方向上更新迭代求解目标函数的等价子问题，从而求得全局最优解。通过计算机仿真实验，可以发现该算法能够很好地平衡重建速度与图像质量，在实际应用中有一定价值。

2 稀疏角度CT图像重建算法

基于压缩感知理论的CT图像重建是近年来研究的热点，其基本思路是先给出目标函数，然后寻找求解目标函数有效算法。

即定义一个稀疏变换为Φ，重建算法可以通过求解以下约束最小问题而实现：

(1)

但是，该问题是数值不稳定的NP问题。基于此，文献[15]于2006年提出了压缩感知理论，证明了l1范数解可以等价于l0范数解。从此，l1范数重建算法被广泛应用。因此可以考察l1范数最小化问题：

(2)

文献[15]还说明精确重建与所在频域的位置无关，这对于稀疏角度重建问题有着至关重要的意义。

本文提出改进的稀疏角度CT图像重建算法，即EPFALM算法，算法流程图如图1所示。

图中算式编号在下文演算过程中均有对应算式。算法的具体步骤如下：

步骤1：

(1) 初始化参数v0、ζ0、λ0、β0、μ0、α、ρ；

(2) 令Xk=XXp当条件满足时停止迭代；

(3) 令αk=ραk，当满足Armijo条件时停止。

步骤2：

(1) 由式(14)，计算Xk+1；

(2) 由式(19)，计算wk+1；

(3) 由式(21)，计算zk+1；

(4) 由式(7)-式(9)，计算新乘子。

2.1 目标函数的建立

在稀疏角度重建问题中，有效方程数量远少于未知数个数，属于不确定问题。文献[7]因此提出了先验图像约束压缩感知PICCS算法，该算法通过在目标函数中加入先验图像，从而弥补图像的不完整，平滑重建伪影。PICCS设定的目标函数为：

(3)

式中：p为先验图像，Φ1、Φ2为任意稀疏变换，α为相对权重。Chen等[7]通过两个独立的步骤数值计算：第一步，使用ART重建算法得到先验图像p；第二步，将式(3)中差图像的TV与目标的图像的TV加权求和。两步计算交替迭代，直到迭代终止。

受Chen等[7]、Xu等[16]和王欢等[17]的启发，提出以下优化目标函数：

minXfs.t.AX=b

(4)

2.2 外点惩罚函数增广Lagrangian乘子法求解

文献[18]的研究说明，用增广Lagrangian方法求解约束问题最优化是适合的。因此，本文提出外点惩罚函数增广Lagrangian乘子法(EPFALM算法)。其本质是连续不断的改变Lagrangian乘子和惩罚因子来求解各异的Lagrangian函数，即使用无约束最小优化方法得到此Lagrangian函数的极小值点。

对于本文提出的优化目标函数式(4)，应用EPFALM，可以将其化为如下问题：

(5)

式中：wi=Di(X-Xp)2,zi=DiX。

相应的Lagrangian函数为：

LA(wi,zi,X)=

(6)

设wi,k、zi,k、Xi,k代表第k次迭代的最优解。通过式(7)-式(9)更新乘子：

vi,k+1=vi,k-βk(DiXk-wi,k)

(7)

ζi,k+1=ζi,k-βk(Di(Xk-Xp)-zi,k)

(8)

λk+1=λk-μk(AXk-b)

(9)

应用EPFALM，可得增广Lagrangian函数为：

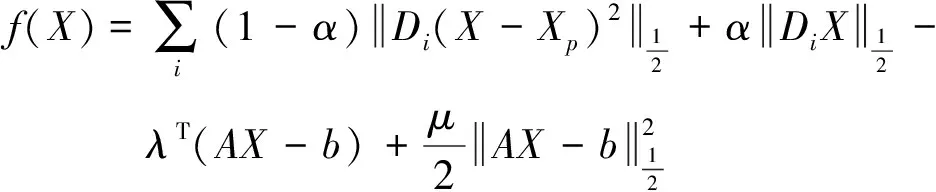
(10)

minXfs.t.AX=b

如果我们引入wi∈R2替换微分变换DiX，并将两者之间的差作为惩罚项加入到目标函数中；同时引入zi∈R2替换微分变换Di(X-Xp)，并将两者之间的差作为惩罚项加入到目标函数中，那么有:

LA(wi,zi,X)=

(11)

将式(11)代入式(10)中,易见目标函数与式(6)相同。

在本算法中，每一步迭代最小化十分重要。文献[10]将变量分离技术首次引入压缩感知，把交替最小化算法用于图像卷积去噪。本文将Lagrangian函数LA(wi,zi,X)的最优化问题转化为三个子问题，通过在交替方向上求解子问题，进而得到最优解Xk+1，计算过程如下。

在X-子问题中，由于

minuLA(wi,k,zi,k,X)=

(12)

式中：wi,k、zi,k、Xp已知。根据式(11)，可求解Xk+1，此问题等价于X-子问题：

minXQk(X)=

(13)

因为Qk(X)是一个二次函数，因此利用最速下降法求解Qk(X)最小化问题:

Xk+1=Xk-γkdk

(14)

式中：dk=dk(Xk)为Qk(X)的梯度。

μkAT(AX-b)-ATλk

(15)

又因为wi,k、zi,k为上一次迭代的最优解，故不能保证全局最优，所以采用一步最速下降法来逼近Qk(u)的最优解。

在迭代过程中，采取Goldstein步长规则，即:

f(xk)+(1-c)αk▽f(xk)Tdk≤f(xk+αkdk)≤

f(xk)+cαk▽f(xk)Tdk

(16)

验证αk是否满足Armijo条件，若α满足:

f(xk+αdk)≤f(xk)+cα▽f(xk)Tdk

(17)

则取ak←a，否则通过αk=ραk(其中0<ρ<1)来减小步长，直到满足条件为止。

在w-子问题中，根据式(11)，同样可求解wi,k+1，此问题等价于w-子问题：

(18)

其解为：

(19)

在z-子问题中，同理，此问题等价于z-子问题：

(20)

其解为：

(21)

值得一提的是，参数的选择也非常重要，本文采用的是文献[19]的方法。即在初次迭代给予参数初始值之后，以后每次迭代都根据需要调整参数，这样极大地提高了算法效率。而其他细节，如满足Armijo条件，如何选取步长等，也需要在迭代过程中根据相应的公式作出调整。这一点在MATLAB仿真实验中也有说明。

3 仿真实验与分析

为了验证算法的有效性，本文进行仿真实验，将使用算法对医学图像进行重建，并与FBP算法、ART算法、Split-Bregman算法与文献[20]提出的UIAL算法做比较。测试计算机的配置为Intel i7-5700HQ CPU@2.70 GHz，16 GB内存。实验使用512×512的Shepp-Logan体模模拟生成的图像。CT图像扫描采取平行束方式进行。实验中所有程序均由MATLAB R2014a编程实现。

为了定量分析图像重建的效果，文献[3]提出，可利用相对均方误差(RRMSE)和条纹指标(SI)来量化重建的效果，其中：

(22)

(23)

式中:X为重建的图像，Xref为原始图像。显然，RRMSE和SI的值越小，表示重建效果越好。

算法中，设定参数如下：

v0=0ζ0=0λ0=0β0=1μ0=256

α=0.5ρ=0.6wi 0=0zi,0=0X0=ATb

每个算法迭代次数为1 000次。

其中，部分参数可以通过式(7)-式(9)更新计算。

vi,k+1=vi,k-βk(DiXk-wi,k)

ζi,k+1=ζi,k-βk(Di(Xk-Xp)-zi,k)

λk+1=λk-μk(AXk-b)

另外经计算得知，当α=0.5时，RRMSE与SI的值最小，因此取α=0.5。当α>1时，RRMSE、SI远高于α<1时得到的值，这也说明了本方法对于CT图像重建是相当有用的。

实验采取的肺部、肝部理想Shepp-Logan体模图像如图2-图4所示。

图2 实验图像

两幅图像用不同算法重建的实验结果为：

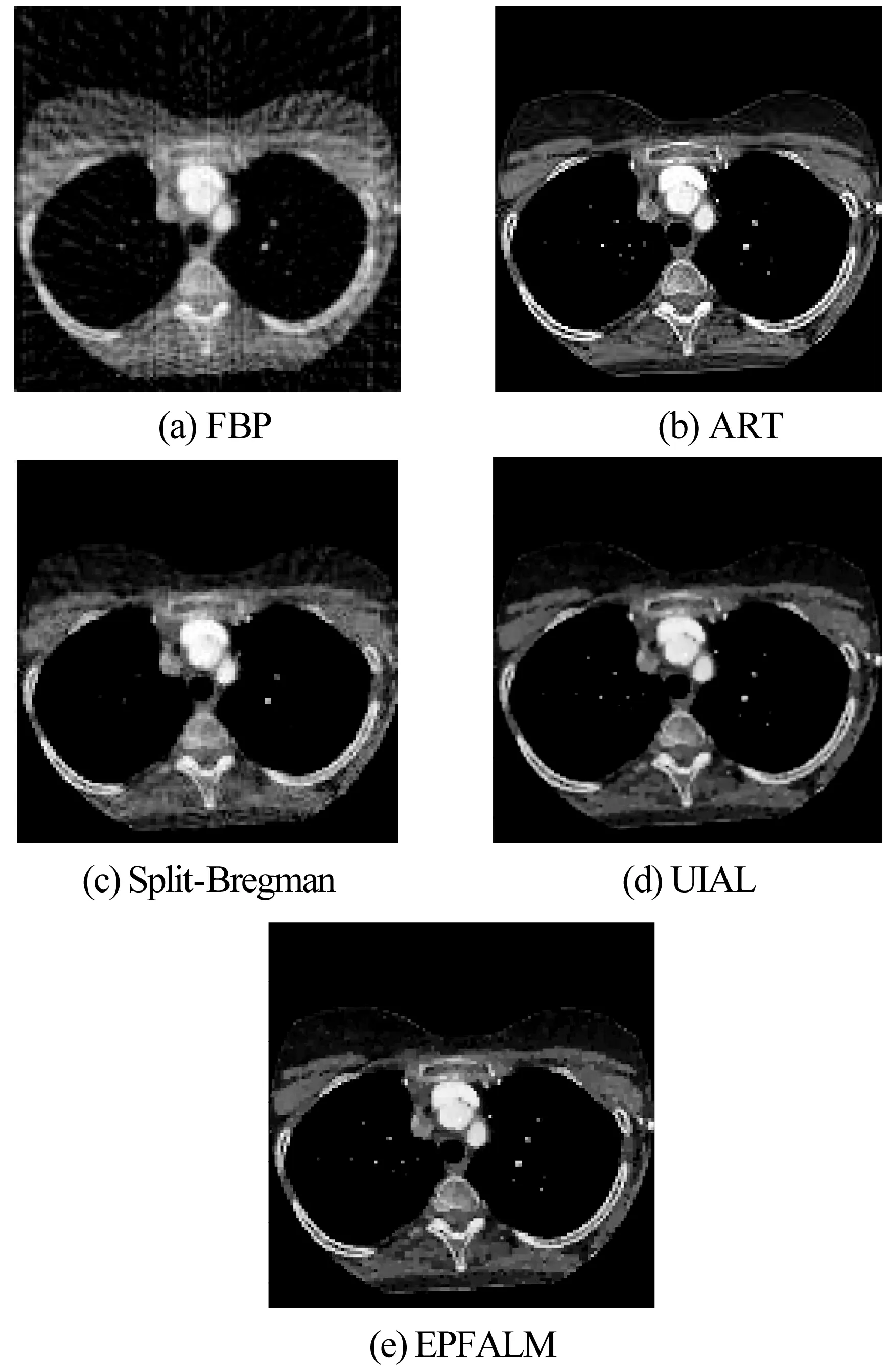
图3 肺部重建图像

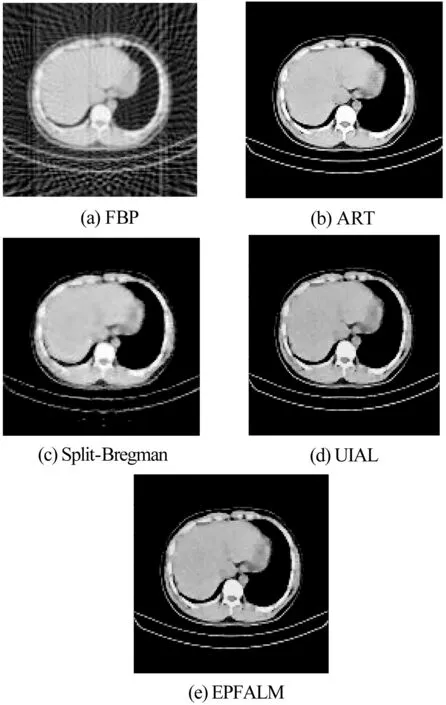
图4 肝部重建图像

图3、图4分别是肺部CT图像、肝部CT图像在稀疏角度采样的情况下重建，五种算法分别为FBP算法、ART算法、Split-Bregman算法、文献[20]提出的UIAL算法和EPFALM算法。从图像中定性分析可知，FBP算法重建图像有严重的伪影，Split-Bregman算法重建的图像细节模糊，而ART算法、UIAL算法和EPFALM算法重建的图像没有伪影，细节较清晰。

下面用评价指标来量化比较各算法下的重建结果。

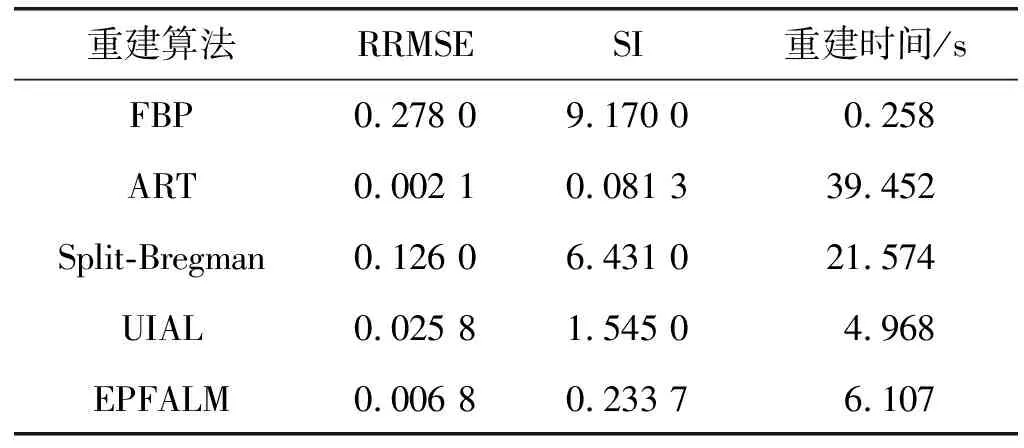
表1 肺部图像重建效果

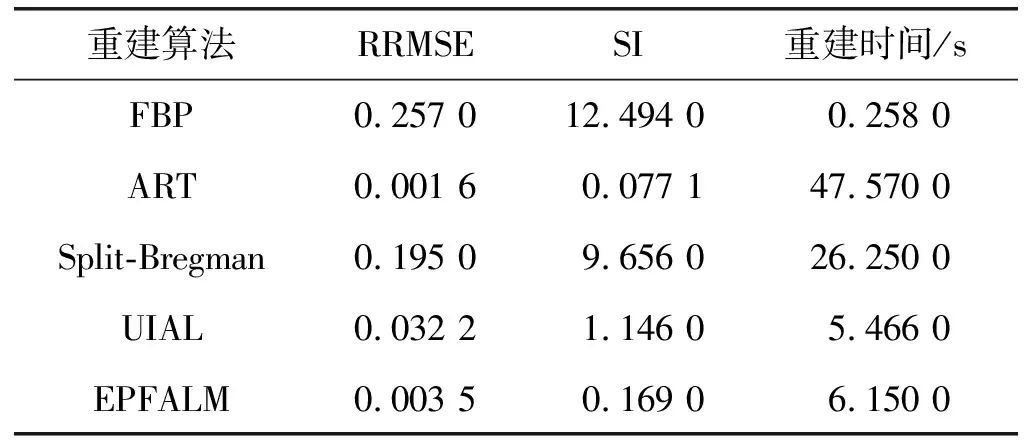
表2 肝部图像重建效果

在重建效果上，EPFALM算法与FBP算法相比，在两幅图像中，RRMSE指标值分别降低97.6%、98.6%，SI指标值分别降低97.5%、92.0%；与Split-Bregman算法相比，RRMSE指标值分别降低94.6%、98.2%，SI指标值分别降低96.4%、98.2%；与UIAL算法相比，RRMSE指标值分别降低74.6%、89.1%，SI指标值分别降低84.9%、85.3%。在重建时间上，EPFALM算法与ART算法相比，降低87.1%；与Split-Bregman算法相比，降低76.6%。