配电网重构遗传算法的个体编码综述

刘延华 李永飞 李 林 郝 欢

1(国网山东省电力公司 山东 济南 250001)2(国网电力科学研究院武汉南瑞有限责任公司 湖北 武汉 438400)

0 引 言

配电网重构是通过变换配电网开关的状态，修改配电网拓扑的过程。其目的包括：1) 能量损耗最小化;2) 保证电压;3) 降低负载;4) 维护负载平衡。值得注意的是，配电网重构是一个实际的生产生活中的复杂问题，被方方面面的现实条件所制约。所以，上述目标往往需要和一些次要目标以及约束条件一起考虑，问题就变得复杂很多。例如，如果同时考虑到设备使用损耗，能量损耗最小化的目标需要伴随另一个次要的目标——开关操作次数最小化。此外，有一些约束条件必须要满足，比如拓扑的辐射性和连通性，支路的限制，总线的电压以及变电站的功率。这些约束有的是连续的，有的是离散的[1]。

从数学角度而言，配电网重构问题十分复杂。因此，这一问题引起了广泛关注。从文献[2]开始起，出现了很多基于贪婪算法求解该问题的研究。其中最主要的两大类是开关交换方法[3-6]和顺序开模类方法[7-9]。不管是开关交换还是顺序开模，最大的优点就是概念简单。然而，这两类方法的本质依然是贪婪算法，局限性在于过于注重局部，难以获取全局最优。

为了获得全局最优解，演化计算被引入配电网重构这一研究领域。演化计算是模拟大自然生物演化过程的，基于群体的，具有自组织、自适应和自学习能力的，求解问题的方法。可以在整个解空间内搜索解，具有获取全局最优的可能性。其原理简单、易于操作、通用性强，而且特别适合大规模并行处理，因此应用极为广泛。演化计算包括很多分支，如遗传算法、演化策略、演化规划、模拟退火、禁忌搜索、粒子群优化以及差分演化等。其中，遗传算法是历史最为悠久，研究程度最高的分支，一直以来都最受关注，最近的一些应用见文献[10-17]。

演化计算的多个分支已经被引入配电网重构这一领域，其中配电网重构的遗传算法为数众多，研究开展得比较充分。

绝大多数演化计算都由杂交、变异和选择三种主要算子所控制。和其他演化计算的类别相比，遗传算法的个体编码以二进制或十进制编码为主，杂交变异十分简便。通常来讲，杂交主要以交换拼接为主，同时，变异也有通用的方法。此外，选择算子是演化计算中通用性最强的，大多数选择算子都可以广泛使用。众多配电网重构的遗传算法之间最大的区别在于个体编码的不同。而编码直接决定了解空间的大小，也就是可行解的数量，从而很大程度上影响着算法的求解效率。基于上述的背景可知，针对各种配电网重构遗传算法的个体编码方式进行总结和分析，对于继续研究配电网重构遗传算法具有重要的意义。

本文对现有的配电网重构遗传算法的个体编码进行综述，从而为配电网重构遗传算法研究的深入提供支持。

1 配电网重构

根据图论，配电网重构问题定义如下[18]。图G包含一系列顶点X和一系列边A，其数学表达为G(X,A)。G中的每一条边ai,j表示一个集合X中两个非源头的元素之间的连接，此处用n(X)和n(A)表达X和A的元素个数。扇区是一个由子基站、总线和无开关支路组成的单元。扇区的边界由具有开关的支路形成，可以利用扇区图来表达一个分布网络——GS(XS,AS)，集合XS组成了网络扇区，AS表示所有的有开关的支路。如果整个系统只有一个子基站，GS就是一棵具有辐射性拓扑的树。如果子基站的数量更多一些，GS则由树集合TS(XST,AST)组成。XST=XS=XF∪XL，XF是由连通边也就是开关闭合的边构成的不相交集，而XL是不连通边构成的不相交集，任何属于TS的边都是连通边。由于XST=XS，每条不连通边都位于TS的两个节点之间，每条不连通边在GS中建立了一个基本的环路。无论GS中存在何样的树集合，不连通边的数量是恒定的。所以，支路的数量和基本的环路也是恒定的。配电网重构就是为了满足能量损耗最小化，或者保证电压，或者降低负载，或者维护负载平衡的目的，对GS进行修改。此外，必须考虑一些实际的电气限制。例如，每个节点必须考虑支路电流热量限制和最小电压，源节点必须考虑子基站功率限制等。

图1是一个配电网的例子。图中：大矩形框表示的是一个单独的子基站，圆形则表示负载总线，小矩形框用来强调有开关的边。

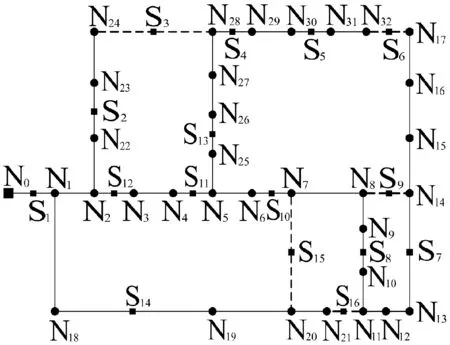
图1 配电网例子

图2展示了根据图1产生的扇区图。扇区图中的节点只有12个，大大低于原分布网络中的33个。所以说，扇区图是对实际分布网络的一种化简表达法。

图2 配电网所对应的扇区图

2 遗传算法

演化计算是模拟自然界中生物的演化过程产生的一种群体导向的随机搜索技术和方法，反映了自然界“物竞天择，适者生存”的思想。遗传算法是演化计算的最大的一个分支，已经在很多领域成功地开展了应用。和其他演化计算方法一样，在遗传算法中始终维持着一个由个体组成的种群，每个个体代表了一个可行解。按照严格的定义，遗传算法的个体是二进制编码的。为了满足各种复杂的应用，可以采用格雷码编码、整数编码、实数编码以及符号编码等。个体代表的解对于当前求解的问题的适应程度即为该个体的适应值。种群中的个体相互之间会发生杂交。在遗传算法中，杂交是通过简单易行的交换来实现的。这也就是遗传算法和其他演化计算的分支相比最大的特点。此外，个体自身会发生变异。同样地，遗传算法的变异也是简单易行的。杂交和变异都产生后代个体，后代个体将和父代个体进行基于适应值的竞争。选择算子负责选出竞争中的胜利者组成下一代种群。上述步骤将循环进行下去，直到满足停止条件为止。

遗传算法具有很多的优点，列举如下[19]。

1) 不需要很多附加的条件，比如可导性等。

2) 具有良好的并行特性。

3) 可用于求解连续、离散或者多目标问题。

4) 能够提供一系列解，而不是仅仅一个。

5) 总是能求出可行解。

6) 当解空间非常大，涉及参数非常多时，十分有效。

遗传算法最大的缺点是：虽然具有寻找全局最优的可能性，但是实际的运行结果可能与全局最优相差甚远。所以，针对一个问题提出遗传算法之后，还需要不断改进，提高算法的性能。个体编码是完成遗传算法的首要问题，必须先于杂交、变异或选择算子进行考虑。

3 配电网重构遗传算法的个体编码

配电网重构遗传算法的个体编码方式多种多样，所决定的解空间大小也截然不同。本节将对现有的多种编码进行详细分析。

3.1 编码方式

为了便于说明，将图2中的扇区图利用各种编码方式进行表达，从而对比不同的编码方式。由图2可见，XS={N0,N1,N2,N3,N4,N5,N6,N7,N8,N9,N10,N11}，而AS={S1,S2,S3,S4,S5,S6,S7,S8,S9,S10,S11,S12,S13,S14,S15,S16}。N0是单独的源节点，其他都是负载节点。由此可知，n(XS)=12，n(XF)=1，n(XL)=11，n(AS)=16，n(AST)=11，n(ANA)=5。

3.1.1 节点编码

各种节点编码方式中，每一位基因表示一个节点。文献[20]中提出的前导法采用了n(XL)位整数基因。每位基因的值均小于n(XS)。图3给出了用前导法表示的个体。图3顶端的一行数字表达的是每位基因的上限，第二行给出了每位基因前导节点的编号，第三行标出每个基因位的序号。

12121212121212121212120123111378141234567891011

图3 前导法表示的个体

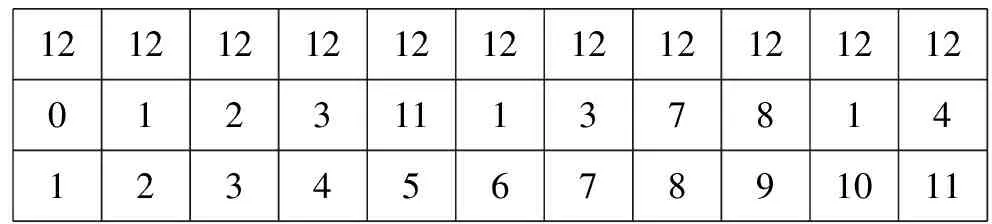
如果在前导法的基础上，根据邻居节点的信息对每个基因位进行限制，可以进一步对编码方法进行改进。基于上述思想，文献[21]中提出了改进的前导法。图4中给出了用改进的前导法表示的个体。在这个图中，顶端一行和第三行的意义和图3中的相同，中间一行的值为0表示该基因位的1号邻居节点是它的源，1表示2号是源，…，P表示P+1号是源。图2中，7号基因位有3个可能相连的节点，分别是N3、N6和N8。按照节点编号决定的顺序，1号邻居是N3，2号邻居是N6，3号则是N8。图4中，7号基因位填的值是0，表示源是N3。

42343232233000020001001234567891011

图4 改进的前导法表示的个体

3.1.2 支路编码

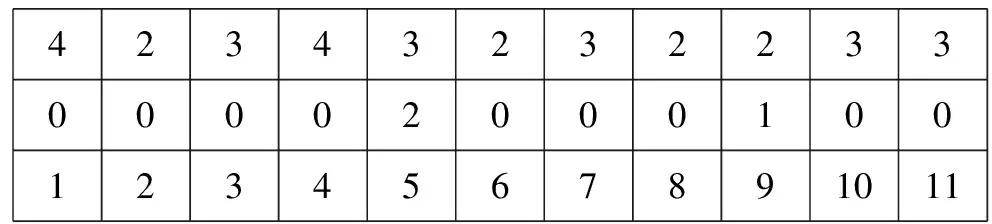
Prufer数法[22]是一种支路编码方式。如果n(XF)=1，则需要从S1到Sn(Xs)-2共n(XS)-2位整数基因。如果n(XF)>1，必须对每棵树都进行上述规则的编码。具体而言，每棵树的支路被从左至右地填入基因位。首先，选择树上具有最小标识符编号的叶子。把与之直接相连的节点的编号填入上述叶子的基因位，这两点就可以确定一条支路。然后，删除前一步涉及的叶子节点及其相关的连接，继续在现存的叶子中选择标识符编号最小的，重复上述步骤。整个循环直到节点数只剩一个为止。根据图2，一开始可选的叶子节点有{0，5，6，9，10}，所以0被选。由于0通向1，所以第一个基因位上填入1；0从叶子节点中被删掉，5被选。由于5通向11，所以第二个基因位上填入11。根据这种方法，可以得到的编码如图5所示。图5中的第一行和前面的图相同，第二行为支路起始端的节点，第三行是按顺序排列的节点号，说明了支路末端的节点。

121212121212121212121111873123412345678910

图5 Prufer数法表示的个体

3.1.3 路径编码

路径编码由文献[23]率先提出。文献[23]中的路径编码需要先进行预处理，找到几条从源节点通向负载节点的路径。其思想是为每一个负载节点开启一个单程反馈路径，从而保证辐射以及连接的限制。由于上述思想的时间复杂度过高，所以需要和一个路径删除算法与之配合。此外，路径还要服从某些规律，所以可行性检验无法避免，拉低了执行速度。由于以上的局限性，这种方法应用不多，在此没有给出示意图。

在文献[23]的基础之上，文献[24]中提出了主链法。主链法表达的一个个体包含了从源节点到TS中的每个叶子节点的所有路径。当然，路径的数量与叶子的数量相等。图6是根据图2得到的基于主链法的个体表达。图6中，每一行各是一条路径，用节点表示，这种表达方式使得个体的长度不确定。

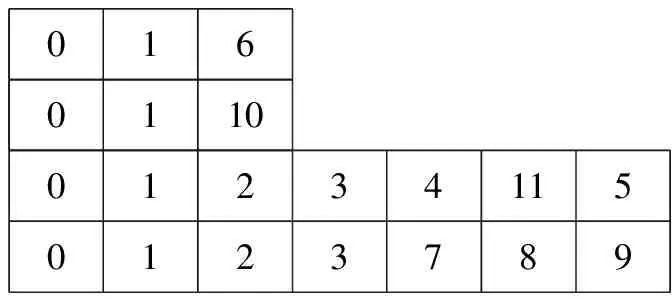
0160110012341150123789

图6 主链法表示的个体

3.1.4 边编码

特征向量法[25-26]属于边编码方式。一共有AS位二进制基因位，每一个基因位表示GS的一条边。取值1表示开关闭合，0表示开关断开。所以，个体表示如图7所示。第一行依然是上限，第二行是基因本身，第三行是基因所对应的边的编号。

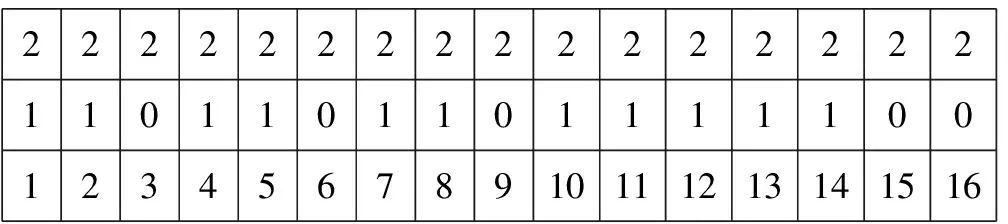
2222222222222222110110110111110012345678910111213141516

图7 向量特征法表示的个体

3.1.5 断开开关编码

断开开关法[27-28]，采用n(ANA)个整数位基因，每位的上限都是AS。每位表达了一个断开的开关。如果用i来表达开关Si+1的话，图2的个体可以表示如图8所示。

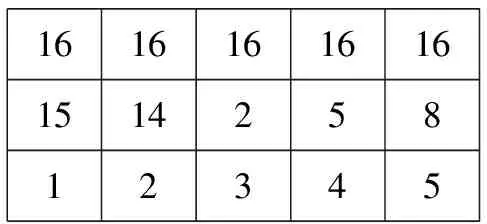
1616161616151425812345

图8 断开开关法表示的个体

3.1.6 环路编码

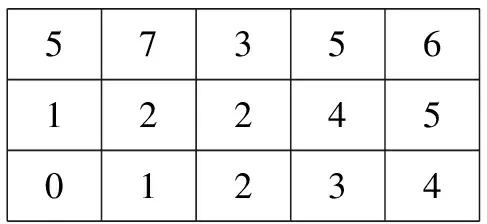
实际上，GS的一个基本环路只会有一个断开的开关。基于上述事实，产生了两种环路编码，不重复环路法[29]和重复环路法[30-31]见图9和图10。这两种方法都需要预先建立一个查找表。在这个表中，每一个回路的各条边按照顺序在同一行给出。表1展示了图2的两种环路编码的查找表。由表1可见，越是编号靠前的回路，其首条边的编号越小。

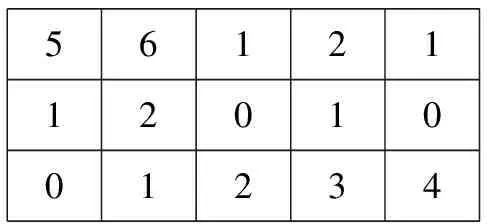
561211201001234

图9 不重复环路法表示的个体

573561224501234

图10 重复环路法表示的个体

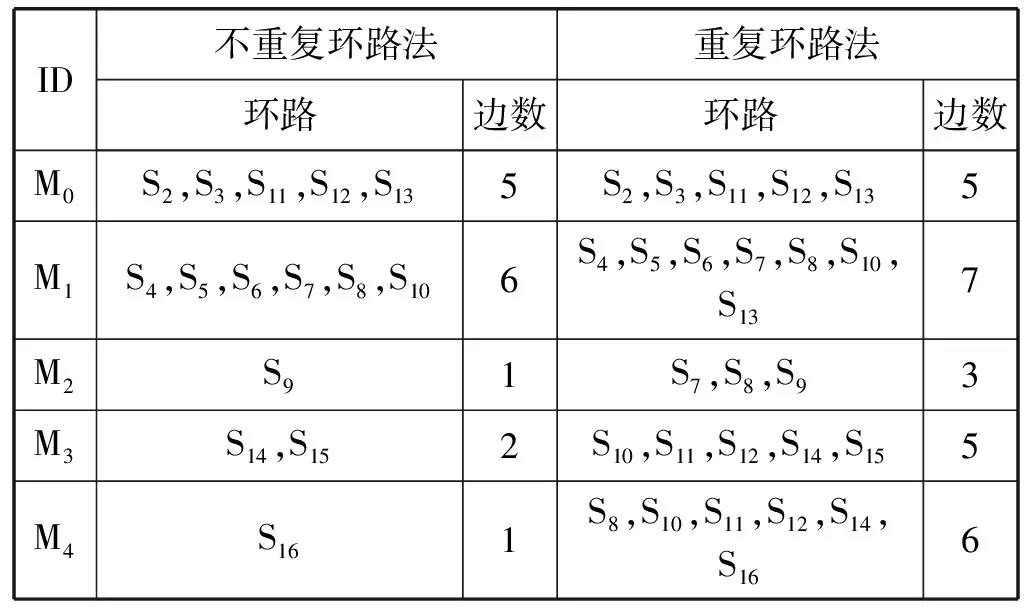
表1 基于图2的不重复环路法以及重复环路法查找表

由表1可见，统计边数时，不重复环路法不会重新将上一个回路出现过的边再次列出。也就是说，若某条边在前面某个回路中列出过，后面的回路即便又用到了这条边，也要在列表中跳过。相反，重复环路法中，重复被利用的边将不限次数的重新列出。由表1可以得到不重复环路法与重复环路法最终的个体编码，如图9和图10所示。在图9中，第一行表示环路中边的数量。第二行表示断开的开关的编号。具体而言，用i代表第i+1号开关。如：由表1可知，M0的第1号开关是S2，用0表示；第5号开关是S13，用4表示。第三行表示环路的编号。图10中虽然有些环路用了更多的边来表示，这是因为重复过的边依然要列出，但是编码的方式是类似的。

3.2 编码的解空间大小

不同编码方式的解空间大小是比较编码方式优劣的重要依据。如果编码方式能够涵盖所有的可行解，那么解空间越小，表示当前编码方式越好。一般而言，解空间的大小可以根据以下公式计算：

(1)

式中：σ是解的个数，也就是解空间的大小。γ是编码的长度，αi是第i位基因的上限。由式(1)可以计算出上述各种编码方法的解空间大小。具体的计算结果见表2。

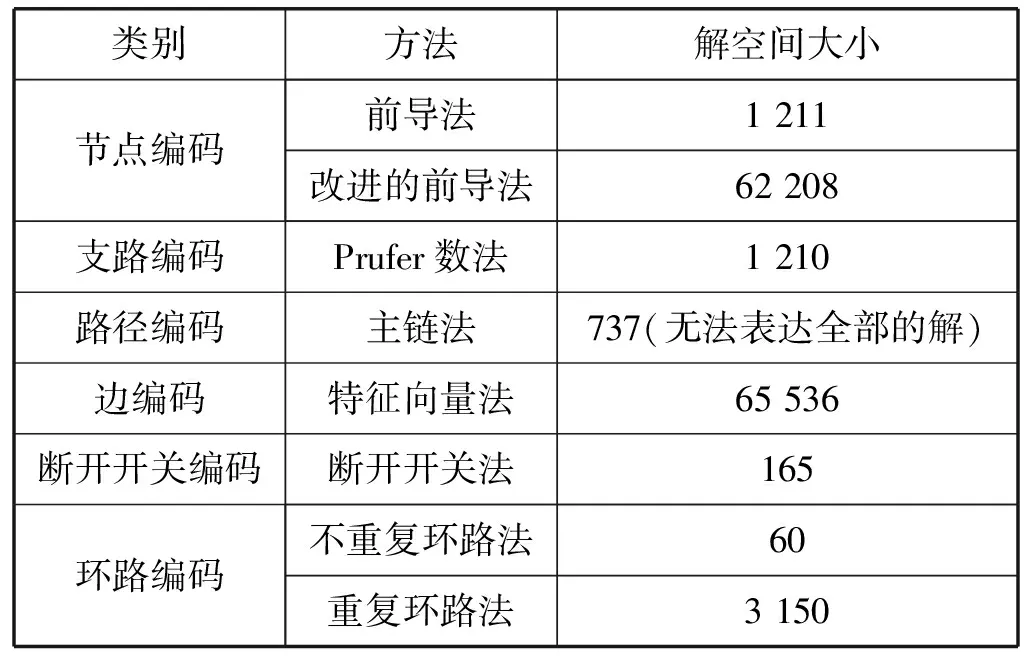
表2 解空间大小

由表2可见，属于环路编码的不重复环路法是解空间最小的编码方法，该方法找出最优解的难度相对最小。

4 结 语

配电网重构是一个复杂的问题。传统的解决方法包括各种贪婪算法。这些贪婪算法的最大缺点是无法找到全局最优解。所以，利用遗传算法求解配电网重构成为研究的热点。然而，配电网重构遗传算法种类繁多，性能还有待提高。

事实上，对于配电网重构问题而言，实施遗传算法的第一个步骤——个体编码是非常关键的，直接决定了算法的性能。本文对现有的各种编码进行综述，并比较了它们所决定的解空间大小。经过比较可见，利用隶属环路编码的不重复环路法表达个体，可以将解空间规模压缩到极致。所以，为了得到更好的配电网重构遗传算法，这种个体表达方式是很好的选择。当然，配合这种个体表达方式的遗传算子也需要进一步改进。