多式联运路径优化模型中的贝叶斯极大熵权重自学习方法研究

张宏博 陈伟炯 闫 明

1(上海海事大学物流科学与工程研究院 上海 201306)2(北京物资学院物流学院 北京 101149)

0 引 言

权重确定的方法分为主观权重和客观权重两个方面。主要的主观权重方法有AHP法[1]、BWM[2]，G1[3]法等，以上方法在确定权重值时主要通过专家经验判断所得，受人为因素影响较大，主要依据目标本身的重要程度来确定量化值。主要的客观权重方法有熵权法[4]、基尼系数赋权法[5]等,其权重值主要依据确权目标的某一具体表现来进行量化计算的，权重的确定受表现的数值影响，会随着评价对象的变化而变化。传统的权重确定方法并不能完全满足实际需要，从近几年的研究可以看出，主客观权重的组合权重确定方法逐渐增多，比如熵权法与德尔菲法的结合[6]，熵权法与AHP发的结合[7]等，它们通过两种方法的结合对传统方法进行了改进，但组合权重的研究仍需要进一步加深。

随着多式联运活动的不断加强，研究也不断加深。研究早期国外的学者就已经通过构建多目标模型来进行路径优化，如文献[8]构建的人群风险等为目标的多目标模型。提出的以生态环境等为目标的多目标模型[9]等。在这些研究所构建的路径求解模型中权重的赋值直接影响到优化结果的合理性。

在本文的研究中提出一种主客观相结合的权重确定方法，并且通过自学习进一步提高其客观准确性。首先通过对目标进行AHP法主观赋权并根据权重区间估计模型得到权重范围，然后通过构建贝叶斯网络和极大熵准则对所得到的主观权重进行自学习，以期得到更加准确的目标权重。而且，采用贝叶斯网络进行构造充分结合了路径优化模型中子目标受多层因素影响的特点，使得到的权重更加客观符合实际。

1 基于贝叶斯网络和极大熵准则的权重自学习

1.1 贝叶斯网络构建

对于多式联运路径优化这种需要构建多目标优化模型的问题，由于其总目标、子目标以及各子目标影响因素相互关联，可以通过构建贝叶斯网络来表达其多层次、多属性的特点，贝叶斯网络能够反映该目标优化问题求解过程中的因果关系[10]。图1为一个基本的多层次、多属性、多目标决策问题的贝叶斯网络图。

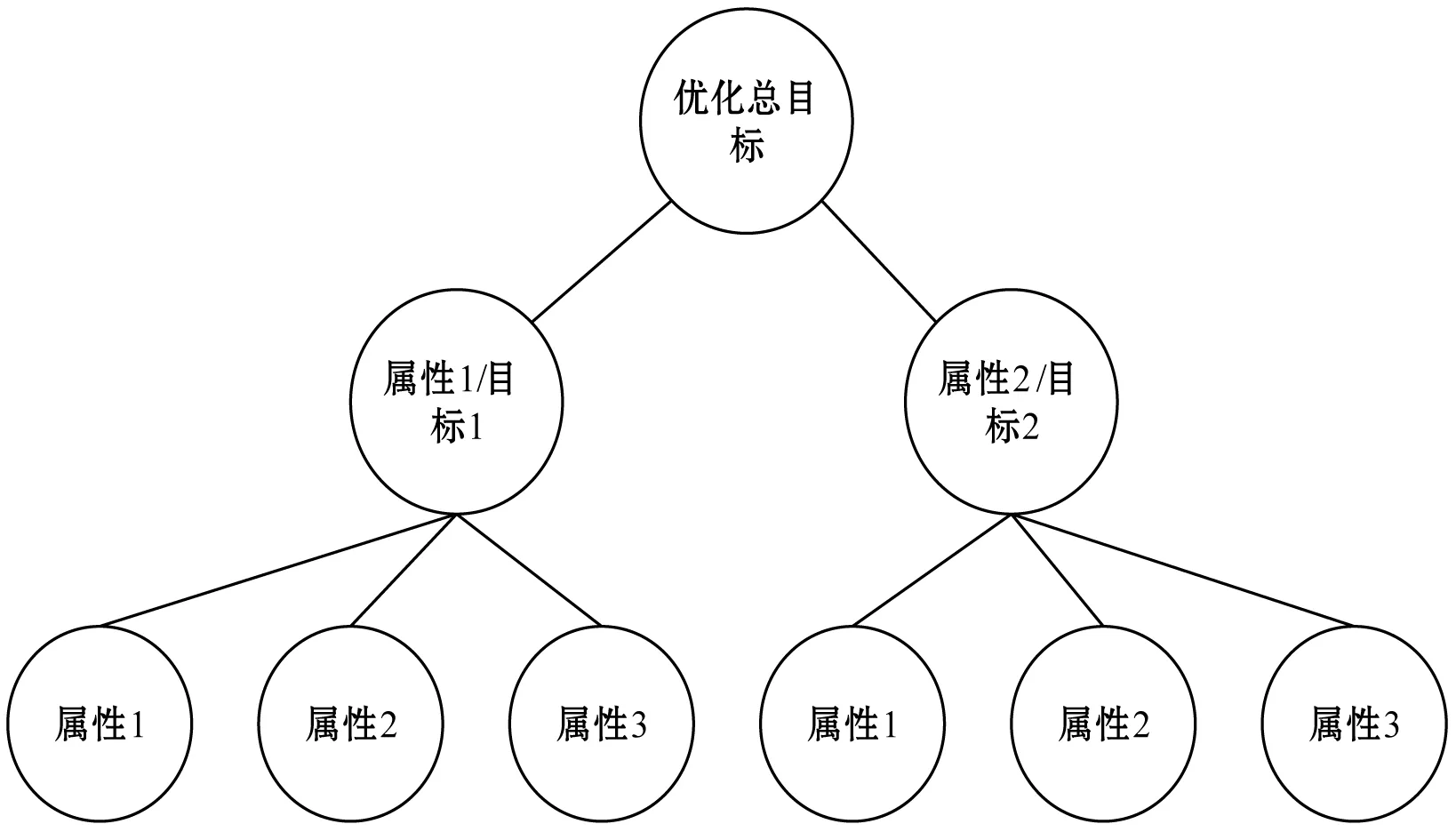
图1 基本贝叶斯网络图

从图1中可以看出，贝叶斯网络图中最高层和最底层是单纯的目标和属性，其余的中间层包含着属性和目标两层含义。中间层对于上一层来说是属性值，对于下一层来说是目标值，不同层级之间的直线表示的是其间的因果关系。

本文中的CPT不是指各属性的条件概率，而是各属性相对于目标的初始权重和属性值，CPT值是贝叶斯网络中的二元结构体，它表示属性相对于其上层评价指标的初始权重和自身的属性值。

1.2 AHP法权重区间估计模型

在自学习的过程中随机变量的生成具有随机性，通过采用区间估计的方法[11]，对随机变量的生成区间进行修正，增强自学习过程中的鲁棒性。

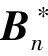
(1)

即：

(2)

根据EM法计算可以得到：

Bn×Wn=βmaxWn

(3)

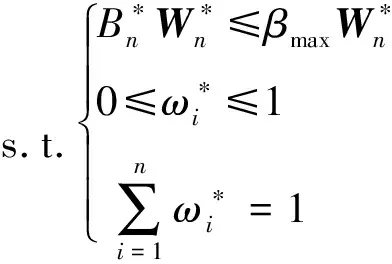
(4)

通过MATLAB计算权重估计模型可以得到APH法的各目标属性的主观权重范围，为自学习过程中随机集合确定范围，进一步把其权重值规定在指定范围内自学习波动。

1.3 信息熵与极大熵准则

Shannon最早吧熵的概念运用到信息论当中，并进一步得到信息熵的理念。信息熵理念是指当得到的信息增多时，所产生的不确定性则会降低，所以用信息熵来定义系统状态的弹性。信息熵基本公式为：

(5)

式中:pi的定义为第i个属性出现的概率，在本文中可以理解为第i个属性的权重值，H(p1,p2,…,pn)为信息熵函数。根据变量的不同对于信息熵的公式定义有一定的区别。

当pi是等概率事件时：

H=-k×n(1/n)ln(1/n)=kln(n)

(6)

当pi是连续变量时引入相关的测度函数c(x)，得到的信息熵的推导公式为：

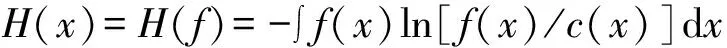
(7)

最先提出了极大熵准则并应用在信息论中的是E.T.Jaynes，根据极大熵准则，应该选择在已知的约束条件下使得熵值(或条件熵)最大的结果作为最客观的结果[12]。熵值最大表示的是客观数据参数的缺少而产生的主观假定最少，从极大熵准则在权重研究中的应用来看，此时的主观因素影响最小，客观性更高。

当变量为概率密度函数时，极大熵准则表达式为：

(8)

式中：R是变量的集合，f(x)为变量的密度函数，Mi是对应第i行的原点矩，b为变量的约束。

在本文中，变量是对应的属性值的权重，变量的集合是离散的点。所以，根据极大熵准则我们可以得出权重的极大熵计算公式：

(9)

(10)

式中：ω为属性的权重值，ωij∈Ni，Ni是贝叶斯网络中同一层级同一目标下的权重的集合。本文将得到的权重值来进行信息熵的计算并把极大熵值作为约束条件，在进行自学习的过程中，将极大熵作为输出条件，使通过自学习得到的权重值更加客观。

1.4 贝叶斯极大熵与自学习的结合

设随机样本为X1,X2,…,Xm其集合为M，ω是贝叶斯网络中某一节点的CPT属性的初始权重值。在路径优化的总目标贝叶斯网络中，其对应的每一个目标下的同层属性值之和为1。如图1中第二层属性1下对应的三个不同属性的ω值之间的关系应该满足ω1+ω2+ω3=1。α定义为在进行自学习优化过程中的一个节点属性，其表示的是上文贝叶斯网络中的一个节点。P(α│Xk)代表的是α节点在随机样本Xk下的先验概率值，相当于自学习过程中的贝叶斯网络的CPT的对应的属性值。

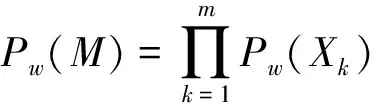
(1) 求梯度。对于贝叶斯网络中的每一个节点上的属性和权重指标进行该节点权重的梯度计算，如公式所示：

(11)

(2) 根据求得的梯度进行迭代。其中d表示为多求得的梯度步长的学习率，d为一个给定的常数。如公式所示：

(12)

(3) 对得到的经过迭代的权重从新进行归一化处理，保证某一节点下的同层的所有属性的权重值满足∑ωi=1。

(4) 设定自学习结束的目标即权重的信息熵达到最大值。对迭代后得到的权重按照式(9)进行熵值计算，当不是最大值时把求得的权重值作为初始权重再次进行迭代求解；当达到最大值时则停止计算迭代结束，输出的结果则是基于贝叶斯和极大熵的结合主客观方法的自学习权重。

2 基于贝叶斯和极大熵的权重自学习步骤

根据前文的步骤陈述，对基于贝叶斯和极大熵的权重自学习进行步骤总结，具体步骤如图2所示。

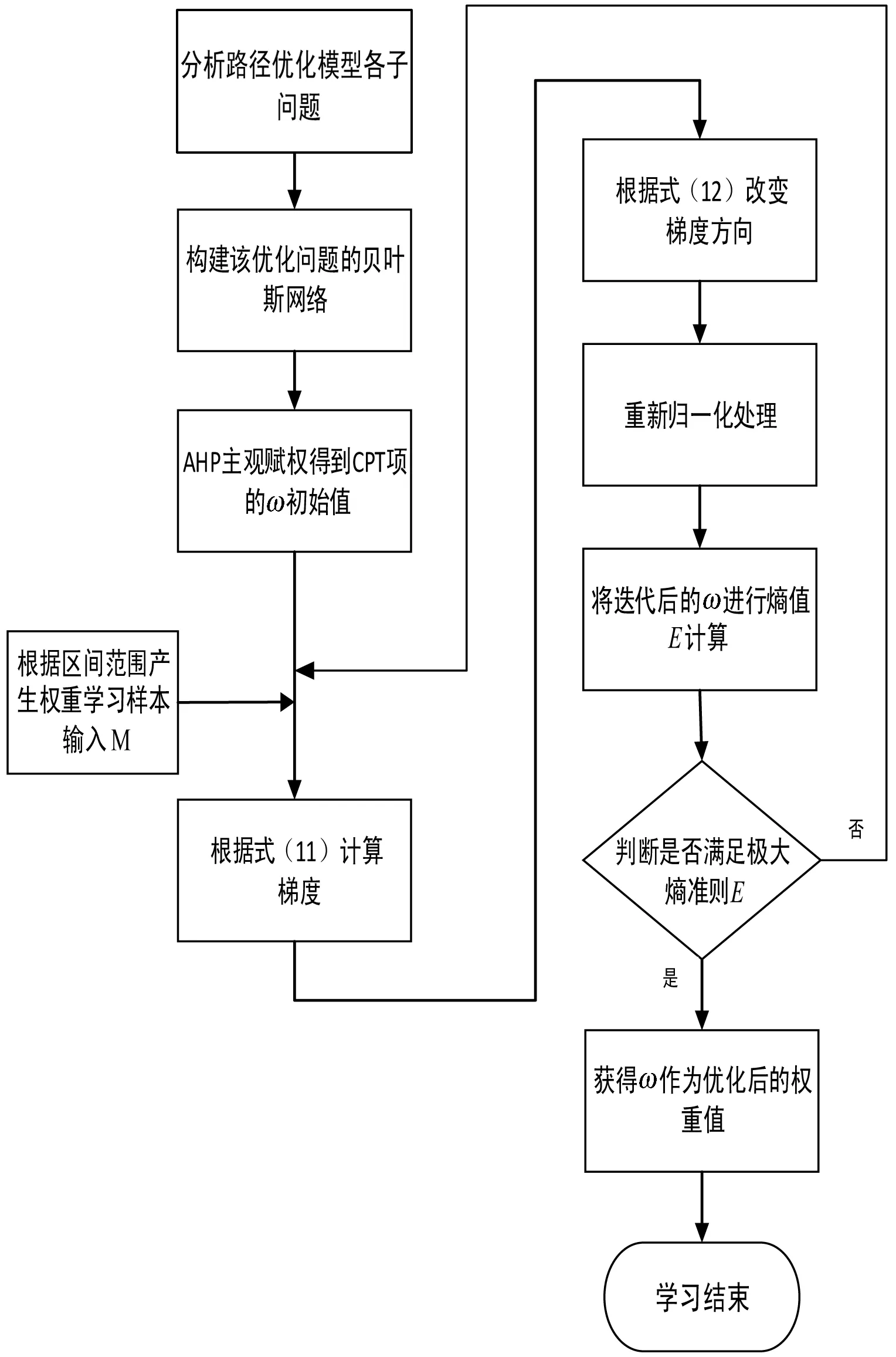
图2 基于贝叶斯和极大熵的权重自学习流程图

(1) 对路径优化模型的子目标进行分析，构建多层次、多目标的贝叶斯网络。

(2) 对构建的贝叶斯网络通过AHP法进行分析得到相应的主观权重值，即自学习运算前的各属性的初始权重值。

(3) 生成自学习的随机样本M，其集合为X1,X2,…,Xm。

(4) 输入极大熵原则方程E作为迭代终止的目标。

(5) 根据本文中提出的基于贝叶斯和极大熵的自学习方法进行迭代学习。

(6) 当得到满足极大熵原则的条件时终止迭代。输出的ωi则是贝叶斯网络中的

对应的各个节点的基于贝叶斯和极大熵的权重自学习方法的最终权重值。

3 多式联运案例研究

本文在进行案例分析时，对危险品的多式联运路径优化模型中的各子目标进行分析并建立贝叶斯网络。危险品运输是众多运输种类中比较特殊的一类，因其发生事故危害较大而备受关注。根据数据表明，95%的危险货物其生产和消费地点有着较大的距离。当运输距离较远时，采用多式联运进行运输更加灵活同时也更加经济。

但是，由于运输物品的特殊性，在多式联运过程中往往需要考虑风险所带来的损失。现阶段国内关于危险品多式联运问题进行路径优化模型构建时也主要考虑成本、时间、风险三个子目标。在对搭建的多目标路径优化求解时，进行的权重确定比较单一，而子目标在总目标中所占的比例直接影响到最优路线的选择问题。采用本文的基于贝叶斯和极大熵的权重自学习方法则是主客观相结合的综合赋权方法可以较为准确地表达各子目标与总目标之间的重要程度。现在本文将以时间、成本、风险为子目标的危险品多式联运路径优化问题进行分析，构建贝叶斯网络并通过自学习方法进行论证。

3.1 构建危险品多目标优化模型的贝叶斯网络图

根据分析得到的基于成本、时间、风险三个子目标的危险品多式联运问题的贝叶斯网络图如图3所示。

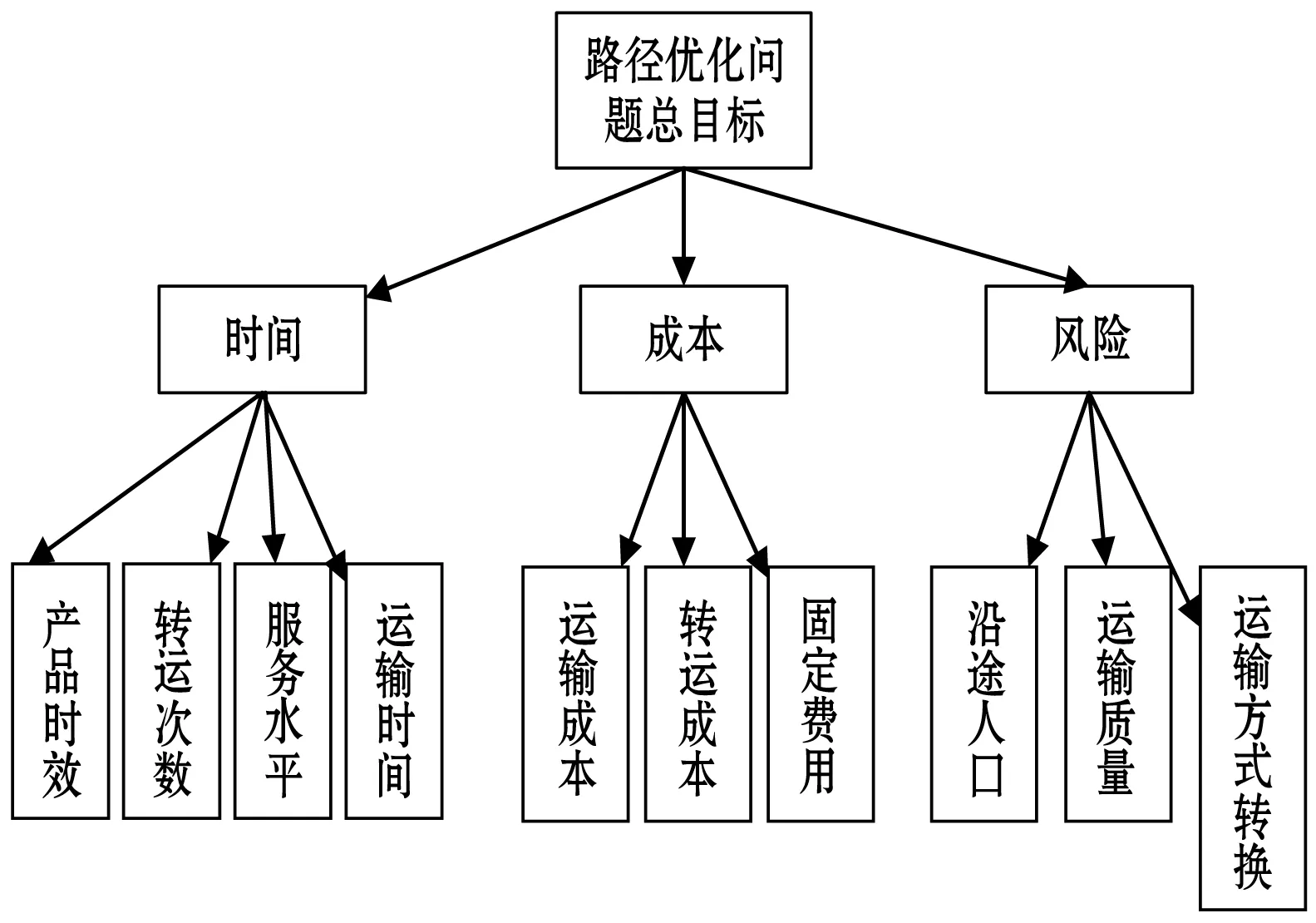
图3 优化目标因素多层次结构图

3.2 贝叶斯网络主观权重自学习求解

(1) 根据图3分析的多式联运优化目标因素多层次结构分析，构建出相应的贝叶斯网络如图4所示。

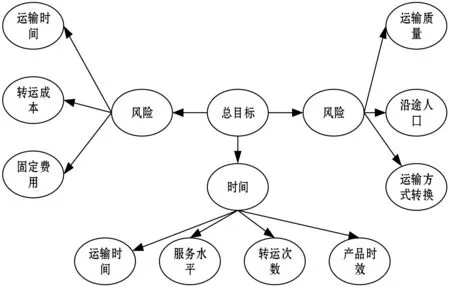
图4 优化模型贝叶斯网络图

(2) 对贝叶斯网络各属性进行层次分析法分析，从而得到相应的主观权重作为自学习方法的初始权重，通过MATLAB对式(4)的区间估计模型进行求解，得到相关数据。考虑到危险品运输其自身的特殊性和发生事故后的影响，对中间层的重要性排序为风险、成本、时间。根据该基础对图3得到的贝叶斯网络的其他属性值进行主观赋权，并作为自学习的初始权重值。

(3) 通过在0-1区间之间生成随机样本，并满足各分支层属性的权重值之和为1。

(4) 根据图2中总结的方法步骤进行权重自学习，设定d的值为0.2作为自学习梯度的学习率，当得到权重熵值最大的权重值时学习结束，输出对应贝叶斯网络的新权重值作为结合主客观方法的权重值。

(5) 对通过AHP法分析得到的主观权重跟本文方法自学习得到的权重值进行分析比较如图5所示。权重数据如表1所示。

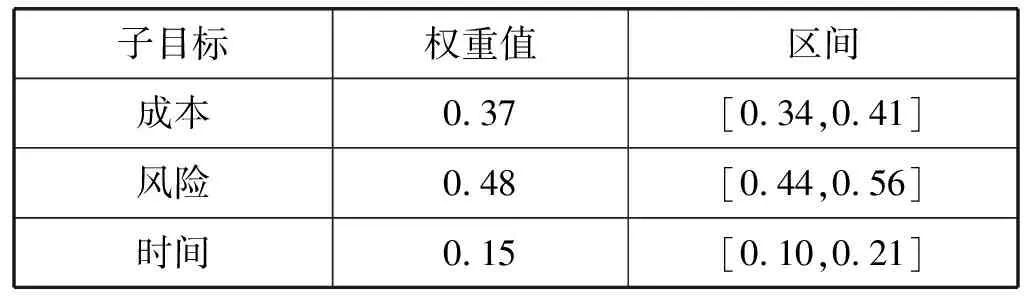
表1 各目标AHP法主观权重值

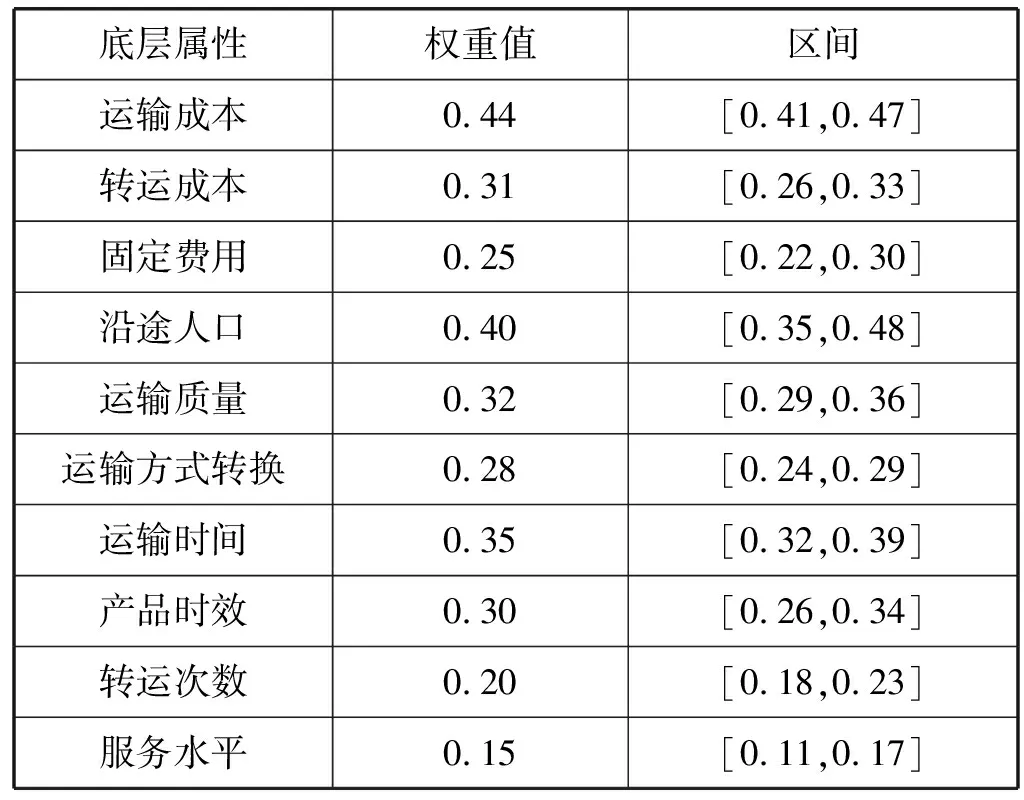
续表1

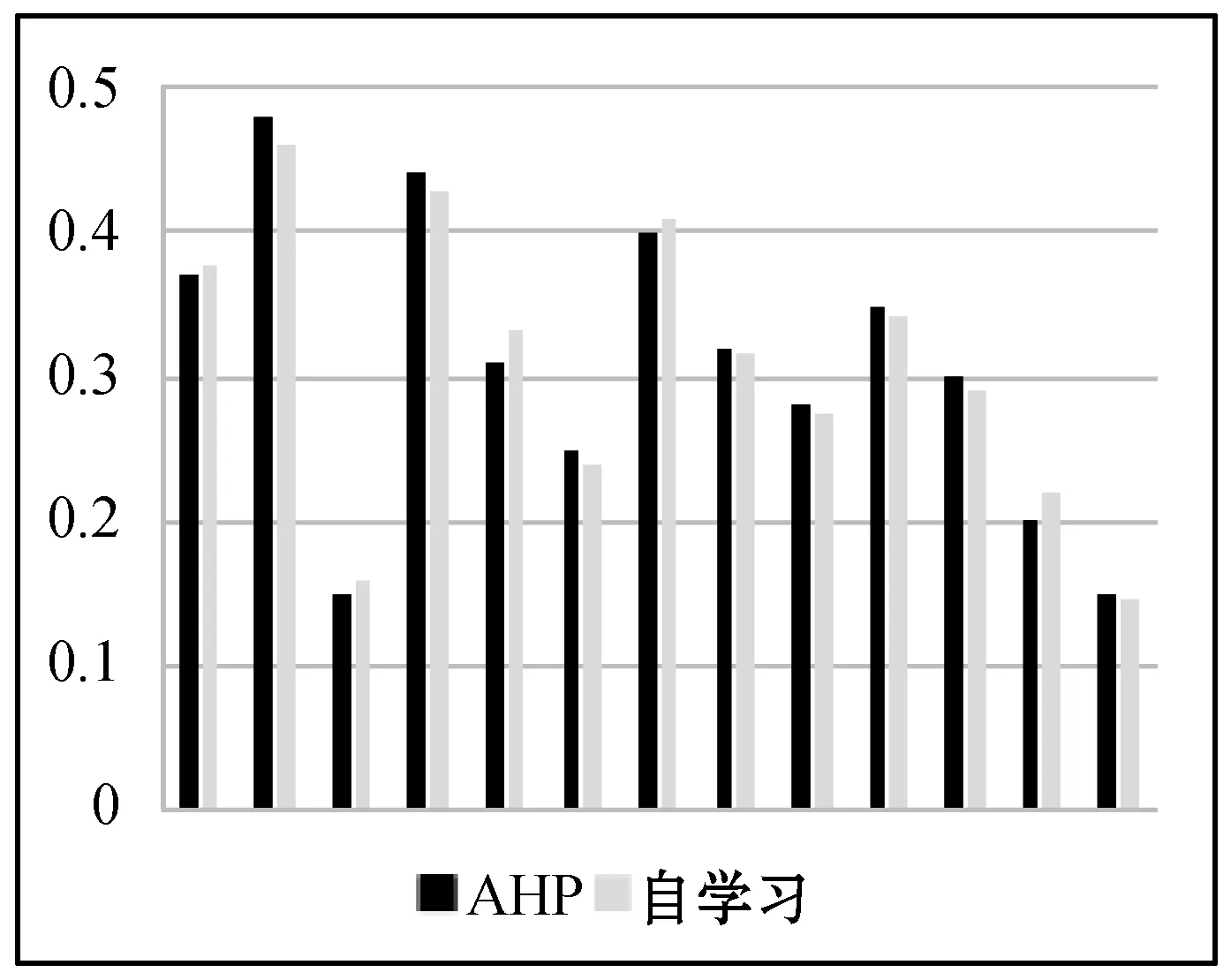
图5 AHP法和自学习得到权重对比图

自学习过程中得到的权重变化如图6、图7所示。

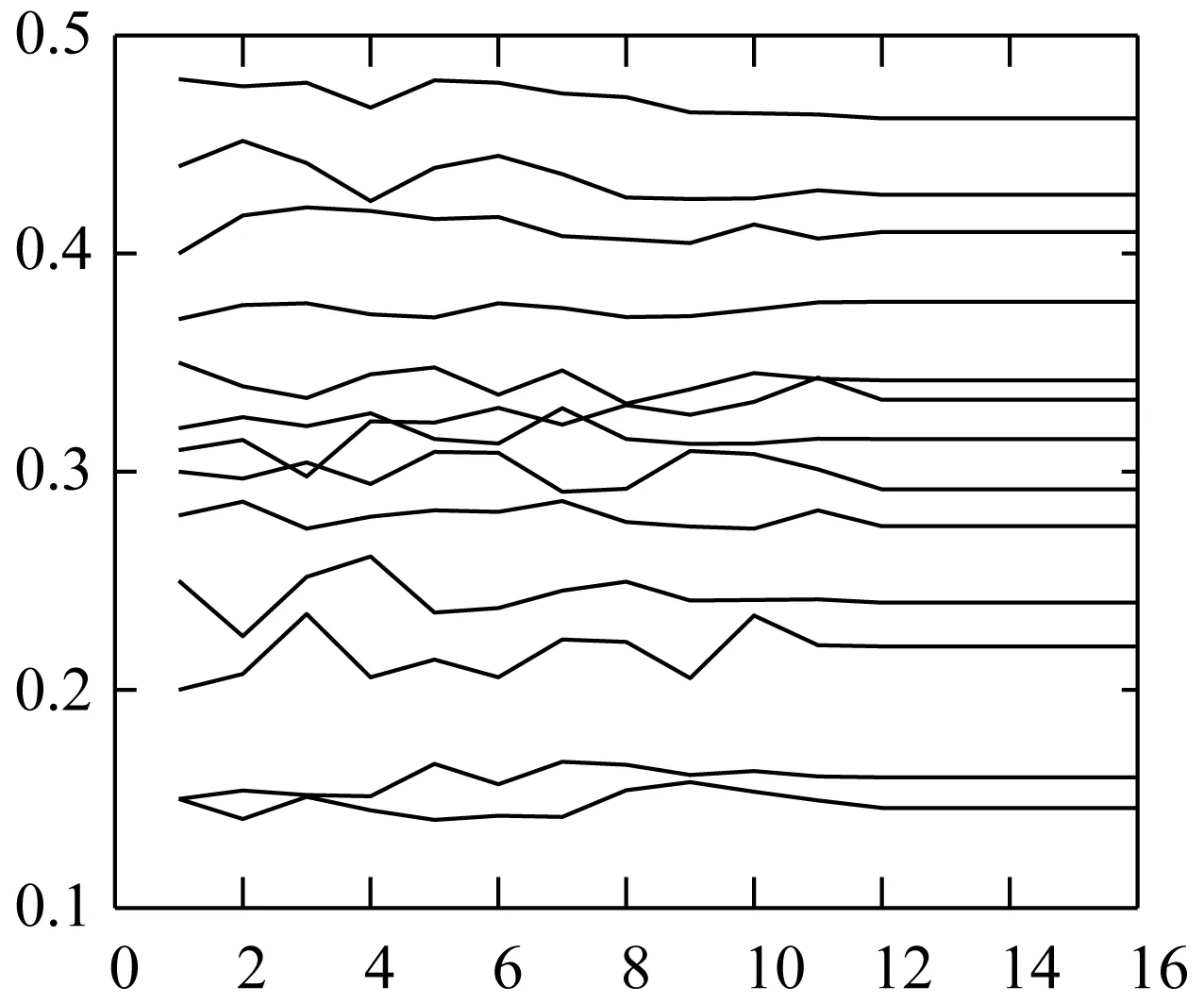
图6 自学习过程中风险权重的变化

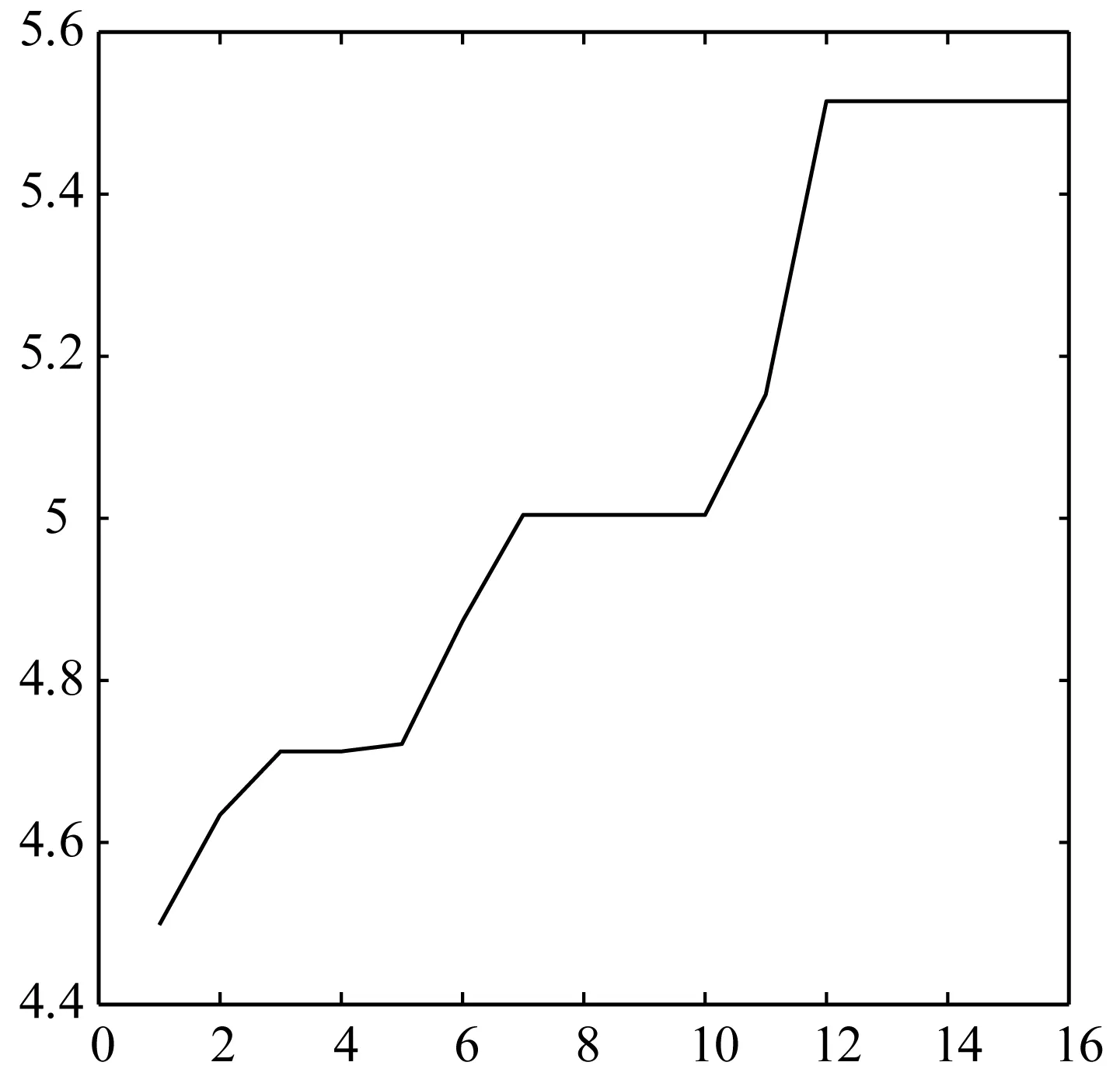
图7 自学习过程中极大熵的变化

根据MATLAB得到的图片可以看出当自学习经过12次的迭代得到符合极大熵准则的客观权重值。根据图5中AHP法和自学习得到的权重之间的比较，可以看出通过两种不同方法得到的权重值总体趋势相差不大但是每个权重值还是进行了细微的改变。通过将主观权重方法和客观权重方法结合，建立了基于贝叶斯网络和极大熵准则的权重自学习方法，并通过该算例说明了方法的可行性和有效性。

4 结 语

在本文中，提出一种新的主客观相结合的权重赋值方法。该方法首先通过构建贝叶斯网络分析优化问题各子目标的相关影响因素，再通过AHP法得到贝叶斯网络中各因素的主观权重值，最后通过基于极大熵准则的权重自学习根据贪心爬山算法进行学习，从而得到更加客观的各目标权重值。

通过该方法得到的权重来求解多目标的多式联运路径优化模型，既可以充分考虑多式联运问题中时间成本风险等子目标间的综合因素，又能通过自学习的方法增加主观权重的客观性减少人为因素对权重值的影响。根据极大熵准则,在已知的主观权重基础上，输出权重熵值达到最大并满足约束条件所得到的权重值为最优的属性权重值。从进行的危险品多式联运的各目标构建的贝叶斯网络进行案例分析可以看出，基于贝叶斯和极大熵的权重自学习方法能够充分契合该问题的多目标和多层次的特点，并结合主客观方法使得到的权重值更加准确可靠，同时吸收了智能算法的求解优点。