自相关函数在机械故障诊断中的应用

李兴慧，李小汝，申永军

（1.四川工程职业技术学院 机电工程系，四川 德阳 618000；2.石家庄铁道大学 机械工程学院，河北 石家庄 050043）

1 引言

在旋转机械故障诊断方面，鉴于齿轮、轴承等旋转机械结构特点，采集的振动信号注定具有循环平稳性，应用自相关函数对振动信号的故障特征提取，已逐渐成为故障诊断领域研究的热点。如文献[1]提出了一种时延相关解调和隐马尔科夫模型相结合的故障模式识别与分析方法，他们首先利用自相关时延对振动信号去噪，提取能量特征后再进行模式识别；文献[2]将时延相关解调成功应用的齿轮故障诊断中，不仅验证了时延自相关解调法能有效解调频，且具有良好的抗噪性；文献[3]利用时延相关函数对实测混叠转子振动信号降噪，再利用盲信号分离技术对降噪后的信号进行分离，在强噪声条件下有效分离出了混叠转子振动信号；文献[4]利用形态自相关和时频切片相结合的故障诊断方法分析了的轴承故障，采用形态滤波和时延自相关方法对含噪信号进行降噪，经频率切片小波变换分解后来提取故障特征；文献[5]结合线调频小波路径追踪算法和循环平稳解调算法的优点，提出了线调频小波路径追踪的阶比循环平稳解调技术，在变转速情况下有效地提取了齿轮故障特征信息；文献[6]将循环统计量理论扩展到复信号，定义了二阶定向循环相关函数和二阶定向循环谱相关密度，揭示转子在指定循环频率处的旋向及周期特性；文献[7]利用循环自相关函数较好的抑制平稳干扰的能力，将其应用到齿轮和滚动轴承故障早期诊断过程中，有效地提取出淹没在噪声中的故障信息。

在工程实际应用中，振动信号一般是利用加速度传感器从齿轮箱箱体上采集得到，但实际得到的振动信号很大程度上受到噪声干扰，往往不能准确反映齿轮箱中各部件的运行状态。为了在采集振动信号中有效提取出故障特征信息，首先利用时延自相关函数（DAF：delayed autocorrelation function）降噪原理对故障振动信号降噪，且降噪仍然保存了故障振动信号的周期特性及差异性，因此，可将时延自相关降噪后的自相关函数作为分析信号。旋转机械的运动部件产生的振动信号中含有特定的周期，特别是运动部件发生故障时，振动信号的统计量多数是呈周期性变化，具有循环平稳性，因此，可以再利用循环自相关函数（CAF：cyclic autocorrelationfunction）将待分析信号进行解调处理，从而在循环域中将振动信号中的周期成分提取出来，即为故障振动信号的特征信息。数值仿真信号与故障模拟信号验证了该方法的有效性。

2 自相关函数的故障诊断方法

2.1 时延自相关降噪原理

在信号分析与处理中，自相关函数良好的降噪特性己广泛得到应用。对于信号x（t）而言，其自相关函数可以表示为：

式中：τ—自相关函数的时延量；T—信号周期。普通周期信号经自相关处理后，原信号中各种特征信息仍很好地保存在自相关函数中，并没有太多能量散失，而普通噪声信号自相关函数在时延接近于零时有很明显的峰值特征，随着时延的增大，其自相关函数很快趋于零。

在实际工程应用中，采集信号一般是故障振动信号与噪声相混合的信号，通常表示为：

式中：y（t）—混合信号；x（t）—故障特征信号；n（t）—噪声信号，且x（t）与 n（t）相互独立。因此，上式的自相关函数为：

因此，时延较低部分主要是噪声自相关函数Rn（τ）的峰值特性；在时延较高的部分，保存了故障信号的基本信号特征，而噪声能量散失十分厉害，主要是自相关函数Rx（τ）成分。由于低时延时噪声自相关函数所占比重较大，剔除此部分以获得滤噪能力较好的自相关部分，从而实现降噪，另外，由于自相关函数无偏估计式的误差对信号分析准确性有较大影响，一般也去掉自相关函数高时延部分[8]，上述过程便是时延自相关降噪原理。

2.2 循环自相关函数理论

信号x（t）的统计特征是随时间周期或多周期平稳变化的，其对称形式自相关函数为：

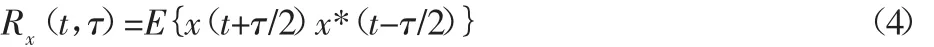
式中：*—复数共轭。如果对所有时间 t有 Rx（t，τ）=R（t+T），则称该信号是二阶循环平稳的，a=1/T被称为基础循环频率。因此可将Rx（t，τ）展开Fourier级数相应的Fourier系数为：

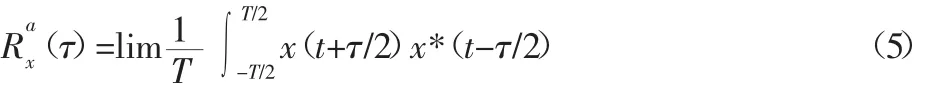
综上所述，时延自相关降噪不仅能很好地降低噪声能量，而且还保留了表征故障振动信号的周期特性，以及故障振动信号中各特征信息的差异性；循环自相关函数则可以将故障振动信号中的周期成分在循环域中有效地分离出来，从而提取出故障信息。根据时延自相关降噪原理与循环自相关函数理论的各自优点，提出了自相关函数的机械故障诊断方法，具体实现步骤如下：（1）首先利用采集振动信号，根据式（2）与式（3）求出采集振动信号的自相关函数Ry（τ）；（2）根据自相关函数性质，去掉低时延部分与高时延部分的自相关函数，保留剩余部分的自相关函数，从而实现时延自相关降噪；（3）由于自相关函数保留了表征原信号基本特征的周期成分，将剩余部分的自相关函数作为待分析信号，再利用循环自相关函数（τ）在循环域中将周期成分分离出来；（4）分析循环自相关函数图中的周期成分，提取表征故障信号的特征信息，判别机械故障类型。

3 仿真信号分析

旋转机械故障诊断中常见的信号类型通常包括：规则周期信号（如正弦信号）、故障振动信号（如调制信号，调频信号）及背景噪声信号。数值仿真信号选择为：

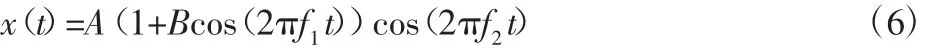
式中：A—载波幅值；B—调幅因数；f1—调制频率；f2—载波频率。仿真信号中的参数值分别取 A=3、B=2、f1=30Hz、f2=400Hz、k=1时，以采样频率为4kHz，采样点数为4096，为更好模拟故障信号，将仿真信号中加入噪声信号（［-1，1］之间正态分布的随机噪声）。

仿真信号无噪声及噪声强度k=4时，直接利用式（5）求出循环自相关函数，得到的无噪信号、含噪信号波形与循环自相关函数频谱图分别，如图1、图2所示。本方法首先根据式（2）与式（3）求出仿真信号自相关函数，然后利用时延自相关降噪，得到剩余部分的自相关函数作为待分析信号，再根据式（5）求出循环自相关函数，其时延自相关降噪后波形与循环自相关函数频谱图，如图3所示。

对比原信号与含有噪声的波形和循环自相关函数频谱图，可以看出，循环自相关函数直接对含噪信号分析，虽能提取出淹没在噪声中的特征频率，但不能有效地剔除平稳噪声的影响，若背景噪声在强时，将很难有效提取出特征频率。在图3中，将时延自相关降噪后的自相关函数作为待分析信号，再通过循环自相关函数将原信号中的特征频率有效地分离出来，此方法不仅很好地抑制了噪声，而且将信号中的特征信息展现在不同的循环频率处，在频谱图中很容易分辨出表征信号的特征信息，从而验证了本方法的实用性。

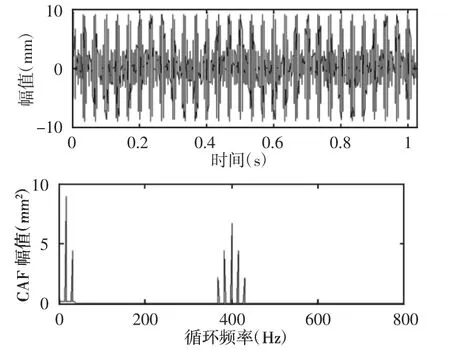
图1 原信号波形与CAF频谱图Fig.1 The Signal and its CAF

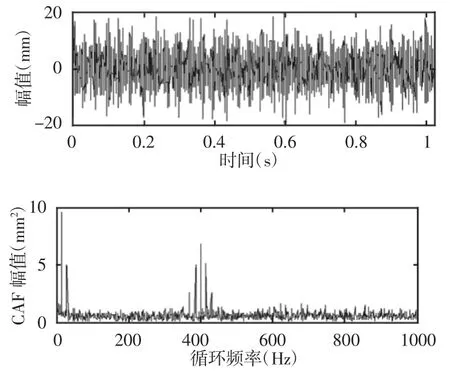
图2 含噪声信号波形与CAF频谱图Fig.2 The Noise Signal and its CAF

图3 DAF降噪波形与CAF频谱图Fig.3 The Denoising Signal by DAF and its CAF

图4 实验平台Fig.4 The Experimental Platform

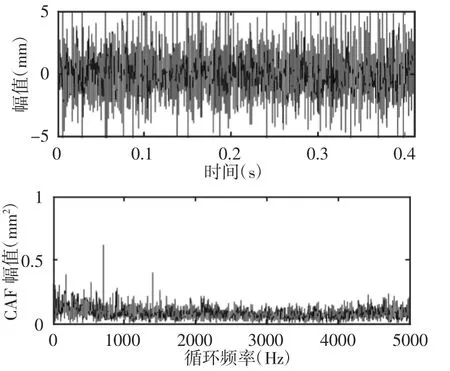
图5 采集信号波形与CAF频谱图Fig.5 The Collection Signal and its CAF

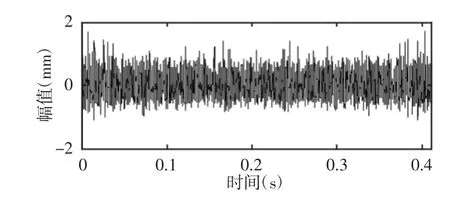
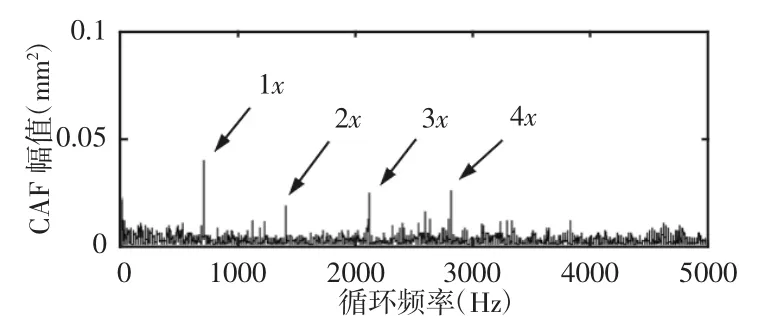
图6 采集信号DAF降噪波形与CAF频谱图Fig.6 The Denoising Signal by DAF and its CAF

4 模拟实验分析

采用江苏千鹏旋转机械振动分析及故障诊断试验平台系统模拟故障信号，试验平台，如图4所示。进一步验证方法的有效性。设备齿轮箱中齿轮对齿数为z1=55与z2=75，选用采样频率为10kHz、转速为770r/min时采集齿轮断齿故障试验数据，采样点数为4096，计算得到的转频、啮合频率分别为12.8Hz、706Hz。直接利用式（5）求出采集振动信号的循环自相关函数，其波形与循环自相关函数频谱图，如图5所示；本方法先利用式（2）与式（3）求出振动信号自相关函数，经时延自相关降噪得到待分析信号，再根据式（5）求出循环自相关函数，其时延自相关降噪后波形与循环自相关函数频谱图，如图6所示。

从采集信号循环自相关函数频谱图中可以看出，在循环频率等于齿轮断齿故障的特征频率（484Hz）时，特征频率的峰值较为突出，其余倍频的幅值则不明显，无法判断是否存在边频信息。从方法降噪后的循环自相关函数频谱图中，不但在循环频率等于齿轮断齿故障的特征频率（484Hz）处有较明显的峰值，而且在2倍频、3倍频、4倍频处均存在较为明显峰值，且在特征频率及倍频处不存在边频信息，另外，也有效降低了噪声信号的能量，提高了信噪比。故障模拟实验结果表明，时延相关降噪方法可以很好地降低噪声的影响，循环自相关函数则有效地在循环域中将故障特征信息分离出来，从而可提取出特征故障频率，准确判别了齿轮故障。

5 结论

由于旋转机械设备自身特点，旋转机械设备振动信号多数呈现循环平稳现象，利用循环统计量的分析方法，可以检测出旋转机械设备的运行情况。在采集振动信号中，往往受到噪声的影响，首先将时延自相关降噪原理应用到机械故障诊断中，有效降低了噪声的影响，再利用循环自相关函数解调原理从循环域中提取出表征故障信息的周期成分。数值仿真结果和模拟实验结果表明，本方法不仅很好地抑制了噪声，而且将信号中的故障特征信息展现在不同的循环频率处，实现了故障特征信息分离的目的，从而准确地判别出故障的类型。因此，在旋转机械故障诊断中，本方法具有较为广泛的应用前景。