滤筒结构对除尘器性能影响的CFD研究

郗 元 ，赵赫民 ，代 岩

（1.大连理工大学盘锦产业技术研究院，辽宁 盘锦 124221；2.吉林大学 机械科学与工程学院，吉林 长春 130022）

1 引言

随着国家加大对空气污染整治力度，对烟尘排放浓度提出了更高要求，大多数企业开始转向有着更高除尘能力、较小的运行费用的袋式除尘器[1-2]。如何有效提高除尘器的工作性能，对于大气污染的防治和治理有着重大意义和深远影响。

文献[3]针对某一大型袋式除尘器在不同流速下流场不均匀度情况进行研究，利用CFD技术计算得出不同流速下不同滤袋流量分配系数；文献[4]结合滤袋不同材质展开研究，以滤袋渗透率和介质厚度作为透气强度的评价标准，通过控制这两个参数实现除尘器中的最佳工作性能；文献[5]对不同长度的滤袋进行CFD数值模拟研究，通过分析流量、压力和速度的分布均匀性，得出袋长为10m的滤袋流量分配最为均匀；文献[6]对除尘器的最佳进气位置进行了模拟分析，为实现高效、耐用的袋式除尘器的最佳入口速度提出了建议。上述研究分别从流量分配系数、材料属性、滤袋长度、入口位置和风速等方面提高了除尘器的工作性能，而并没有关注市场上常见的不同结构滤筒形状，如圆形滤筒，椭圆形滤筒，圆台形滤筒，矩形滤筒对于流场均匀性的影响。

通过建立不同结构滤筒的计算流体力学模型，分析不同结构滤筒内气流分布规律，以流量分配均匀性和滤袋表面过滤风速作为评价指标，对不同滤筒结构下除尘器的内部流场展开数值分析，确定不同滤筒结构的选用标准。

2 物理模型及数值计算

2.1 模型参数

结合国内某型号袋式除尘器，其箱体主要尺寸为（800×800×1000）mm，进风和出风口尺寸为均为（300×300）mm。选取市场上常见的滤筒结构及常规尺寸，保证总过滤面积相近，各滤筒（袋）结构尺寸分别为圆形滤筒φ325×660、椭圆滤筒365×290×600、圆台滤筒 φ320×φ220×750、矩形滤筒 325×215×600、滤袋 φ140×1000。利用CREO3.0对流道模型进行构建，如图1所示。

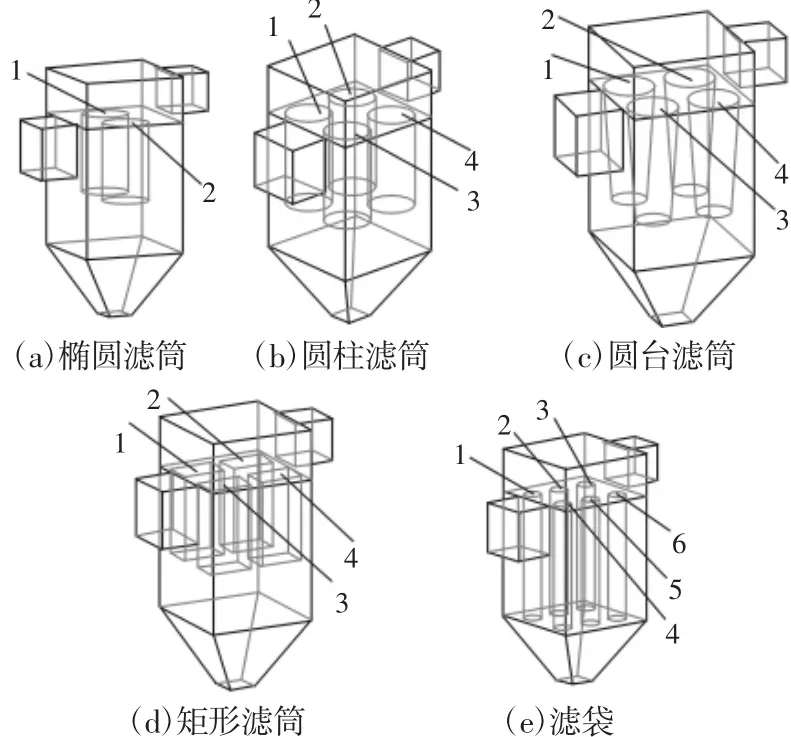
图1 不同结构滤筒模型流道模型建立Fig.1 Flow ChannelΜodel of Dust Collector

2.2 边界条件及算法选取

除尘器此时处理风量工况为1945m3/h，因此各区域边界条件设置如下：气流流入处设为速度入口，速度大小设为6.0m/s；气流出口设为压力出，设为标准大气压；滤袋表面选择多空跳跃边界条件，渗透率设为8×10-9，滤袋厚度设为2mm，其余壁面均设置为不可移动壁面。求解方法选用SIMPLE，选择二阶迎风格式，其相比于一节迎风格式具有更高精度，且不会引起假扩散现象[7-8]。

3 结果与分析

3.1 流量分配均匀性

流量分配系数是单个滤筒（袋）含尘气体处理流量与所有滤筒（袋）含尘气体平均处理流量之比。

式中：Ki—i（i=1，2，3…n）号滤筒流量分配系数，值越接近1.0，表明流量分配越均匀；Qi—i号滤筒含尘气体处理量（m3/s）；Qm—平均含尘气体处理流量（m3/s）。数值模拟计算，如表1所示。其中滤筒（袋）编号对应图1中各滤筒（袋）的编号。

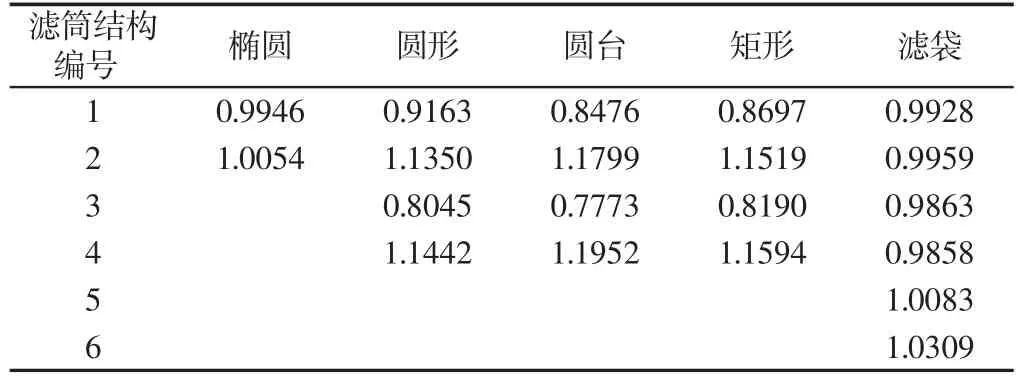
表1 不同结构筒（滤）袋流量分配系数Tab.1 Flow Distribution Coefficient of Filter Cartridge（bag）

滤袋结构和椭圆结构流量分配最为均匀，四筒结构（圆形结构、圆台结构、矩形结构）流量分配系数在数值1.0周围波动较大，表明流量分配最不均匀。其中后排滤筒（2号滤筒和4号滤筒）处理含尘气体流量较大，后排滤筒容易损坏。对比圆形、圆台和矩形结构可知，圆形滤筒效果较优。

最大流量不均匀幅值是同一结构中最大流量与最小流量分配系数之差，如式（2）所示。

式中：△Kqi—最大流量不均匀幅值，最大流量不均匀幅值△Kqi≥0，且该值越接近0，表明流量分配越均匀；Kqimax—最大流量分配系数；Kqimin—最小流量分配系数。不同结构最大流量不均匀幅值，如表2所示。

表2 不同结构最大流量不均匀幅值Tab.2 Maximum Flow Uneven Amplitude

表3 不同结构综合流量不均匀幅值Tab.3 Copositive Flow Uneven Amplitude

由表2可看出，圆台滤筒最大流量不均匀幅值最大，圆形滤筒与矩形滤筒相差不大。椭圆滤筒和滤袋最大不均匀幅值最小，分析结果与之前相同。由最大流量不均匀幅值也可看出，圆形滤筒△Kqi=0.3397，为三者之中最低，再次证明了圆形结构较圆台结构和矩形结构较优。而圆台滤筒流量分配最不均匀。

为综合考虑各个滤袋流量分配偏差，对流量分配进行全面评价，引用综合流量不均匀幅值△进行评估，如式（3）所示。

式中：N—某结构下滤袋个数。

3.2 滤袋表面过滤风速分析

为准确分析滤袋表面过滤风速分布情况，采用文献[9]的方法，将不同结构滤筒（袋）等面积分为8份，每两份交接处设为一条数值线，以圆形滤袋为例，数值线划分示意图，如图2所示。由于除尘器悬挂滤筒结构均关于中间截面y=523左右对称，故只需提取除尘器一侧滤筒进行分析。同时，采用x.y方式进行不同滤筒（袋）表面数值线位置描述，其中x表示该模型下滤筒（袋）编号，y表示具体哪条表面数值线，如圆形滤筒1.1，即为1号圆形滤筒中1号表面数值线。在椭圆滤筒上，如图3所示。

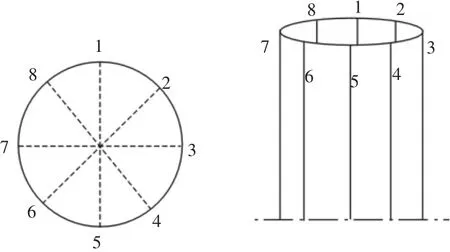
图2 滤袋表面数值线划分示意图Fig.2 Numerical Line Partition on Filter Bag Surface

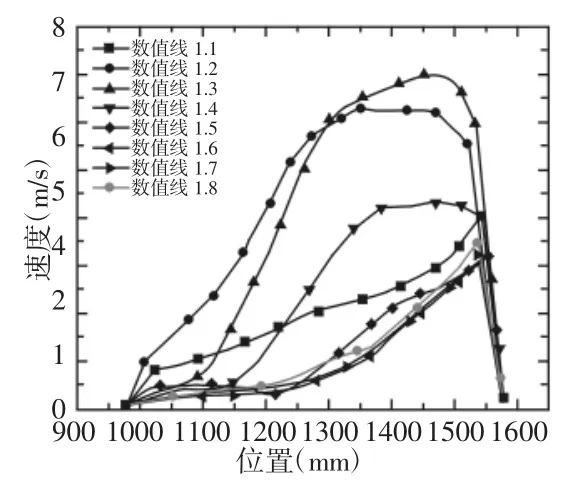
图3 椭圆形滤筒结构半侧数值线上速度分布Fig.3 Velocity Numerical Line of Oval Cartridge

数值线1.3位于两滤筒交接间隙处，数值线1.2则是位于射流直接冲刷区，与圆形滤筒滤袋间隙数值线速度小于射流直接冲刷区数值线相同，椭圆滤筒数值线1.3速度最大，其次是数值线1.2。这主要因为同排两滤筒间隙过小引起的。数值线1.3最大速度达到9m/s左右，数值线1.2最高速度也达到8m/s左右，且整体速度远高于圆形滤筒结构，说明椭圆滤筒极易损坏。

圆形滤筒结构半侧表面数值线，如图4所示。如图可知靠近入风口的两条数值线（1.7和1.8）风速最大，前排滤袋与后排滤袋交界处速度最低，处于该区域的数值线1.3、1.4速度最高为2m/s；靠近壁面的数值线1.1、1.2由于受到沿着壁面伸展的回流影响，速度稍大。对于后滤筒，整体速度明显比前排滤筒小得多，后排两滤筒间隙处数值线2.7速度最大，射流冲击区速度约为6m/s。

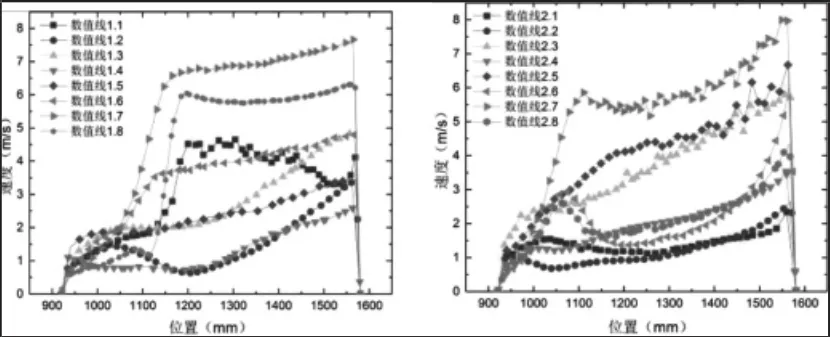
图4 圆形滤筒结构半侧数值线上速度分布Fig.4 Velocity Distribution of Circular Cartridge Numerical Line

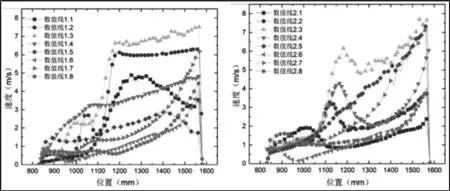
图5 圆台滤筒结构半侧数值线上速度分布Fig.5 Velocity Numerical Line of Circular Truncated Cartridge

圆台滤筒结构半侧数值线上速度分布，如图5所示。其中圆台滤筒前后排滤筒在1200mm到1580mm入射区域滤袋表面速度分布相似，同排滤筒间隙处速度最大（数值线1.3），最大速度约为7m/s。射流直接冲刷区次之（数值线1.2），最大速度约为6m/s。但是由于圆台滤筒结构沿着垂直方向横截面越来越小，使得两者在非射流影响区差别较大，圆台结构下部分速度分布整体较小，但是数值线1.2在1050mm左右突然阶跃，且幅值较大，最大值接近3m/s。圆形和圆台滤筒表面速度大体相似，但圆台滤筒非射流影响区气流分布不均匀。对比矩形滤筒，如图6所示。在入口射流影响区速度最大，气流入射口处最大速度在6m/s附近波动，非入射射流影响区滤袋表面速度大多小于1m/s，明显优于前几种结构；对比后排滤筒，与圆形和圆台滤筒相似，最大速度接近8m/s，但矩形滤筒处于高速区的滤筒面积较小，整体看矩形滤筒数值线速度分布较为平滑，说明气流相比之下较为均匀，且整体速度较小，因此矩形滤筒为最理想四筒结构。

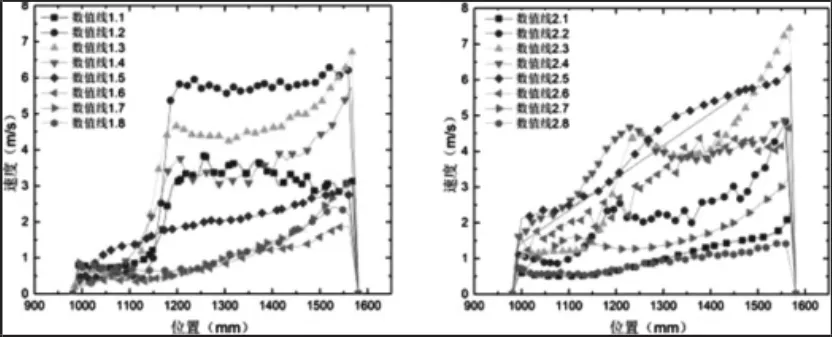
图6 矩形滤筒结构半侧数值线上速度分布Fig.6 Velocity Numerical Line of Rectangle Cartridge

滤袋结构半侧数值线上速度分布，如图7所示。滤袋结构前、中、后排滤袋速度分布相似，前排滤袋速度最大是由于靠近入射口，受到入射射流直接冲刷，而后排滤筒受到射流冲击壁面形成的沿壁面伸展高速回流影响。由于最大速度较大，使得滤袋极易破坏。综上所述，对于五种结构的横坐标在1200mm到1580mm区间内速度都明显高于其他区域，这是因为1200mm到1580mm处为进风口位置，该处滤袋收到告诉射流冲击，使得过滤速度过高。此外还可以看出，1200mm以下，即远离进风口，速度整体为递减的趋势。通过以上分析，对于滤袋表面速度分布矩形滤筒最优，圆形滤筒次之，椭圆滤筒和滤袋最差。

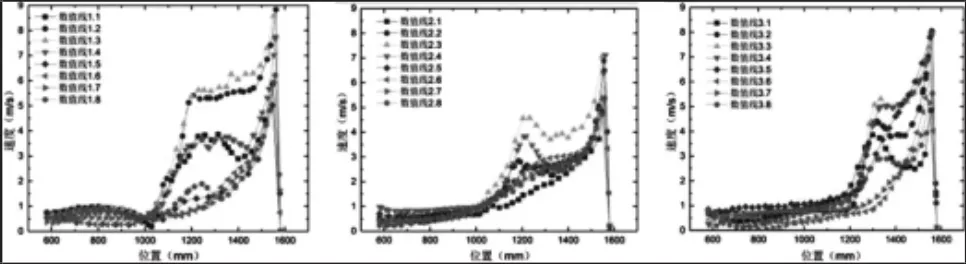
图7 滤袋结构半侧数值线上速度分布Fig.7 Velocity Numerical Line of Filter Bag

4 结论

圆形滤筒最大流量不均匀幅值△Kqi为0.3397，综合流量不均匀幅值△为0.1396，且各筒流量分配系数接近1.0，综合考虑各流量分配系数，圆形滤筒流量分配较合理，使用寿命较长。根据滤筒（袋）表面过滤风速数值线分析法，得出矩形滤筒表面速度较小且均匀，圆形滤筒次之。在常规工况四筒结构布置时，建议选取圆柱滤筒或矩形滤筒作为除尘器过滤滤芯，内流场最为理想。