“时间尺”带来的思考

安徽省宁国市津南小学 毕椿水

“24时计时法”是人教版小学数学三年级下册的一项教学内容。教参中教学建议明确提出“借助几何直观，帮助学生理解抽象概念”，在2013版人教版教材编写中，也特意增加了“时间轴”（笔者认为对学生而言，“时间尺”比“时间轴”更容易接受）部分内容。

但在教学实践中不少教师忽略了这根“时间尺”的存在，用自身的经验，高估了学生的生活经验基础，认为只要带领学生分析情境图中一天24小时中不同的时刻所做的事情，引发学生对普通计时法与24时计时法认知冲突，导入两种计时法的对比教学，进而总结归纳出两种计时法的互化规律，学生就能迅速掌握这部分内容。其实这样的教学处理，会使学生对这一看似简单的学习内容，很难做到深刻理解，当遇到相应的经过时间计算时，更是只能照葫芦画瓢，知其然，而不知其所以然。笔者在一次课后，通过调查发现：班级中只有70%的孩子能说清楚两种计时法间的互化方法及理由，还有30%的孩子只能处在似懂非懂、照葫芦画瓢的阶段，没有达到我们预定的教学目标。因此，笔者也再次深入思考：教材编写时为什么要设置这幅“时间尺”的图片呢？学生能不能直接通过这根“时间尺”发现两种计时法之间的相互关联呢？有了“时间尺”又会给我们的教学带来什么样的变化呢？

一、巧制“时间尺”，建构24时模型

笔者认为，要想借助“时间尺”帮助学生理解两种计时法间的相互关系，必须让学生亲历“时间尺”的制作，这样运用“时间尺”时才能说出原因来。

斯苗儿老师提出：“在教学导入时，要尽快暴露学生的经验，从而引发学生学习的动机；教学展开时，要让学生的经验充分展现，从而激活思维，深刻理解。”所以笔者在情境导入时，撇开了教材中的情境图，直接出示下面图片（如图1所示）。

图1

问题：假如我今天出差，买了上面这张火车票，在家里这个钟面的时刻出发去火车站，合适吗？（设计这个问题的目的：唤起学生对“24时计时法”和普通计时法的认知基础，让教师及时掌握学生的生活经验，便于下一步的教学调整）再引导学生对这两则信息展开讨论，达成共识：1.这里火车发车的时间是确定的12时15分（24时计时法表示的）；2.现在的时刻是不确定的11时45分（钟面是普通计时法表示，每天会有2个这样的时刻），如果这个钟面时刻是上午11时45分，赶紧要去车站准备上车了，但要是晚上的11时45分，就已经错过上车时间了（或需在车站等很长时间）。从而引导学生进一步把自己所掌握的“24时计时法”与普通计时法之间互相转化的办法表述出来，及时了解学生已有的经验基础。（这样设计的目的是为了抓住学生已有的经验基础，引发认知冲突，激励学生结合自己熟悉的情境掌握计时法，建立两种计时法之间的联系。同时，在抛出问题后，驱使学生自觉运用已有经验分析问题、解决问题，从而体验到数学的价值）

情境导入后，再次引导学生观察钟面（图2），进一步复习钟面上时针每天会转动2周，就出现了2个相同时刻，人们为了区分这2个不同时刻，所以出现了在前面加上“时刻词”——上午、下午、晚上等，来记录时刻的普通计时法。接着，笔者提出一个设想：假如我们用剪刀从钟面12这个点剪开，把这个本来圆形的表示时刻的线拉直，会怎么样？并引发学生的思考：这时数字12要放在拉直的这条线段的什么位置？（生：靠右侧的端点上）那左侧的端点怎么办？对比我们手头的直尺，看看有什么想法？（生：左侧标上 0）（如图 3）。

图2

图3

形象地把圆形的钟面转化成学生习惯的直尺，同时激发学生探究的兴趣，构建出初步的时间尺的模型。有了这样的基础，然后再思考，每天时针会转动2周，那就是说这样的“尺子”在一天当中也会出现2“条”，但时间是不会间断的，我们怎样把这2“条”尺子也不间断地连接起来呢？让学生自己想办法解决——把0与12重合（如图4）。这个问题的设计就是为两种计时法间互化时理解“+12”和“－12”做好铺垫。并追问：要是有3“条”这样的尺子呢？这次的追问，进一步让学生想到当第3条尺子合并过来，这条尺子上表示的是第二天中的第一圈时间，所以24时既是第一天的结束，又是第二天的起始时刻（0时）。这也为后面的经过时间计算时的“分段”做好铺垫，从而引导学生完善“时间尺”（如图5），明确昨天、今天和明天的关系，形成24时模型。笔者认为学生有了这样的“时间尺”创造经历，才能为下一步的探究做好充分准备，比教材的直接呈现，更有利于学生对知识的深刻理解。

图4

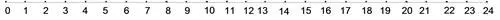
图5

二、妙用“时间尺”，理解两种计时法的关联

构建好“时间尺”后，接下来就让孩子们思考：1.对于这把尺子上，出现了2组1～12的数字，怎样才能更好地区分这2个相同数字的时刻呢（图6，图7）？（激励孩子想到在数字前面加上“时间词”的方法表示，也就是普通计时法）2.按照尺子（数轴）上数字的书写方法，当第一个12出现后，下一个数字怎么表示？请在时间尺的上方对应点上，重新把这组数字表示出来！（帮助学生建立钟面、时刻与数轴之间的相互联系，同时直观对比“24时计时法”与普通计时法的书写，建构24时模型，深入体会两种计时法之间的互化方法，从而熟练掌握）

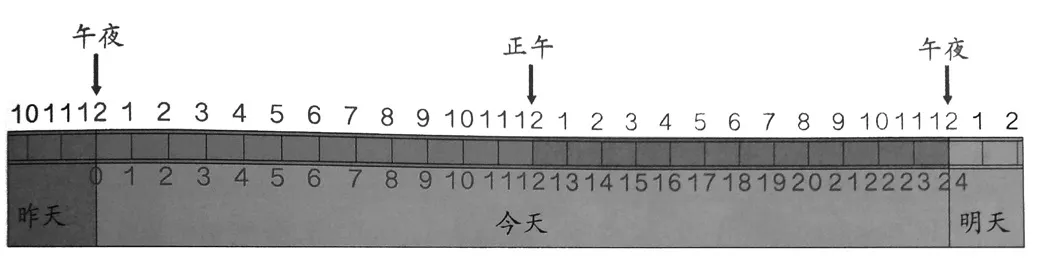
图6

图7

对比这根“时间尺”上下方的两种计时法，学生很快就发现：在普通计时法前面要加“时间词”，一般上午6时前称作晚上，6时到7时称作早晨，8时到11时称作上午等，这样有助于学生对时间词的选用有一个直观的认识和记忆。同样，在下方24时计时法中，从下午1时起，是时钟走的第2圈，所以要开始“+12”来进行转换。进而总结归纳出普通计时法与“24时计时法”的区别：1.普通计时法在数字前面要加上“时间词”；“24时计时法”前面不用加“时间词”。2.普通计时法从1时至12时，最多只能到12时，而且每个时刻在一天中会出现2次；“24时计时法”是从0时至24时，同一天中没有重复时刻出现。

通过这次修改后的尝试，笔者再次调查了授课班级学生情况，竟然95%的学生都能说出普通计时法与24时计时法之间的转化规律，大大提高了这节课的教学效率。在这个教学环节中，笔者的目的是借助“时间尺”这一工具，通过猜想、实验、验证的方法，基于学生的经验，展开教学活动，规划统一的探究路径，同时又不束缚学生的思维，让他们展开想象的翅膀，亲历“时间尺”的形成过程，帮助学生建立两种计时法的联系，并把细碎的知识结构化、系统化，形成两种计时法间转化的技能。

三、巧用“时间尺”，解决时间计算问题

其实，笔者认为“时间尺”的应用，主要不在“24时计时法”的认识上，它更大的作用是帮助学生理解相关时间的计算。学生有了前面亲历“时间尺”的形成经历，在进行相关经过时间计算教学时，设计2个环节逐一展开探究——同一天内的经过时间计算和跨天的经过时间计算。

在同一天内的经过时间计算环节（如图8），笔者让学生直接在“时间尺”上标出发车时间9时和到站时间下午6时，引导观察这时的“时间尺”，很快发现下午6时就是24时计时法中的18时（6+12=18时），再回忆在二年级学习用刻度尺测量物体长度的办法（特别是不是从0刻度做起点测量时的方法：末端刻度－起点刻度=物体长度），形成知识的迁移，从而掌握直接用“24时计时法”时的到站时刻减去发车时刻来计算坐火车的经过时间：18-9=9（小时），体会“24时计时法” 在实际计算中的实用性。

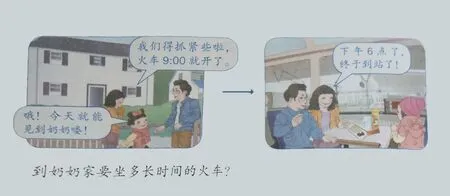
图8

而跨天的经过时间计算，对于一名9岁儿童来说，还是有一定困难的，他们的困难突出表现在难以理解如何进行分段来测算！为了突破这个难点，笔者在前一节课上就特意设计在学生把2“条”0到12的“时间尺”合并后，追问：要是有3“条”怎么办？帮助学生理解掌握第一天的24时也就是第二天的0时，揭示24时就是相邻两天的分界点。然后结合具体的实际问题加以分析：王老师准备去郑州旅游，今天21时在宣城火车站上车，明天早晨7时在郑州站下车，王老师乘坐火车共用了多少小时？学生读题后会发现，这是跨今天和明天的一个跨天时间计算，对照前面的“时间尺”就会发现，这两天的分界点就在24时（0时）。这样很快就得出24-21+7=10（小时）。这次的“时间尺”运用，不仅快速帮助学生找到解决这类问题的办法，还向学生渗透了用每天为一个时间段的方法的“分段”解决问题思想，测算出跨天情况下的经过时间。这样的设计，一方面让学生体会到学以致用的思想——“时间尺”除了帮助我们进行两种计时法的互化，还能帮助我们解决更多的实际生活问题；另一方面借助“时间尺”这一几何直观呈现，帮学生学会把复杂的数学问题变得简明、形象，有助于形成探索解决问题的思路，培养他们的应用意识和创新意识。

数学是抽象的符号体系，是相对感性的另一种理性的表达方式。笔者通过这次思考后调整的教学，就是想通过巧制“时间尺”，帮助学生构建24时模型，引导学生经历一个“具体—表象—抽象—符号化”的过程，把一些分散的教学资源系列化，建立“24时计时法”这类时间单位类型教学的立体架构，体会到系统知识体系在日常生活中的回归，从而促进学生解决问题、自我梳理知识能力的真正提升，感悟学习数学知识的价值所在——更好地帮助我们解决实际生活问题。