无轴承旋翼摆振模态阻尼识别技术研究及其应用
2018-10-19张仕明胡和平
张仕明,周 云,胡和平
(直升机旋翼动力学重点实验室,中国直升机设计研究所,江西 景德镇 333000)
无轴承式旋翼具有操纵功效高,敏捷性好,可靠性高,维护简单等特点,为第四代直升机水平的重要标志之一。无轴承旋翼以柔性梁的弹性变形,代替传统三铰功能,一般设计成摆振柔软式。因此,一般需加装额外的阻尼器保证稳定性。
无轴承旋翼采用的阻尼器通常为液弹或黏弹橡胶式,都具有非线性特性。其等效线性阻尼和等效刚度随桨叶旋转频率、装机质量等呈非线性关系。且装机地面试验中测得的信号频率成分复杂、噪声干扰大,这都增加了准确识别系统的频率和阻尼的困难。
旋翼摆振模态阻尼识别方法,早期采用Johnston等[1]的移动矩形窗法(FFTMB),也是目前最普遍的一种方法,但由于噪声、谐波振动、近频等因素影响,准确识别系统阻尼仍存在许多困难。Smith等[2-3]根据阻尼的机理和类型,进一步发展了基于傅里叶级数的移动矩形窗方法(FSMB)和希尔伯特变换方法(HT)识别模型旋翼的非线性阻尼,并做了误差分析;Ruzzene等[4]分析了采用小波变换方法(WT)识别频率和阻尼。Hu等[5]在Froude相似模型旋翼上发展了应用以上四种方法的模态阻尼识别技术。
本文针对无轴承旋翼摆振柔软,一阶摆振频率和旋翼旋转基频相近,提出了基于序列二次规划(SQP)的小波中心频率和带宽优化选择方法,发展了一种基于FFTMB、FSMB、Hilbert、Wavelet[6-10]的旋翼摆振自由衰减时域信号阻尼识别技术,并成功应用到全尺寸无轴承旋翼装机条件下地面试验的桨叶一阶摆振模态阻尼识别。
1 全尺寸(无轴承)旋翼模态阻尼识别技术
为从旋翼装机地面试验的自由衰减响应中识别桨叶的摆振模态阻尼,本文发展了如图 1所示的旋翼模态阻尼技术。首先截取桨叶摆振自由衰减响应信号,利用初步FFT分析得到的主模态频率估计,采用Kaiser窗函数法设计一个带通零相位数字滤波器,过滤高频噪声和干扰信号,截取滤波后信号衰减段并进行频率优化分析。在准确识别桨叶摆振模态频率的基础上,采用FFTMB、FSMB、Hilbert、Wavelet 4种方法识别出自由衰减信号幅值包络线,取对数后用最小二乘法拟合,根据拟合直线斜率与阻尼的关系,计算得到等效线性阻尼。综合比较阻尼识别结果,最终优选得到摆振模态阻尼。

图1 新阻尼识别技术Fig.1 New damping identification technology
1.1 模态频率识别
精确的模态频率是阻尼识别的关键之一。频率识别的首选方法为测量稳态激励下的频响函数(如正弦扫频),通过设定稳态激励时长T,即可确保高频率分辨率。
当没有稳态数据时,通常用FFT分析自由衰减响应。根据FFT变换原理,长度为T秒的信号xT(t)通过快速傅里叶变换后得到频谱的分辨率是Δf=1/NΔt,N为窗口中数据点个数,Δt为采样间隔,即频率分辨率取决于采样点数和采样率。而阻尼自由衰减信号时长较短,频率分辨率较低,通过FFT分析得到的峰值可能与信号真实频率不一致,导致阻尼识别误差增大。
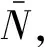
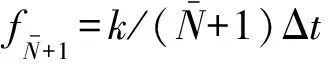
该频率优化方法的频率分辨率为
Δf=k/N(N-1)Δt
有效提高了有阻尼固有频率的频率识别精度。
1.2 阻尼识别方法
FFTMB、FSMB、Hilbert、Wavelet 4种模态阻尼识别方法流程如图 2所示。
FFTMB是基于FFT的移动矩形窗法,由于频率分辨率和阻尼估计精确性之间的矛盾,其受窗口长度影响较大,不适合用于非线性阻尼识别,通常选择窗口长度为数据长度的1/4到1/2。
FSMB法是FFTMB法的改进和发展,其瞬时幅值是基于傅里叶级数计算的,窗口长度为Nc(整数)周期,对单自由度系统,取Nc=1即可。对多自由度系统,本文通过比较幅值对数曲线与拟合直线的方差σNc,衡量模态是否分离,选择合适的窗口周期数Nc。
Hilbert法中,信号经过希尔伯特变换仅仅使得信号的相位改变90°,而信号的幅值不改变。以原信号为实部,变换后的信号为虚部进行求模,即可得到幅值包络线。由于Hilbert变换的边缘效应,在进行最小二乘法拟合时一般选取20%~80%的数据进行计算。Hilbert法不受窗口长度影响,具有较强的非线性大阻尼识别能力。
Wavelet法中选用Morlet复解析小波对信号作连续小波变换,它是一种时间窗和频率窗都可以改变的时频局部化分析方法,其在小阻尼状态具有较强的模态分离能力和较高的阻尼识别精度。
Morlet小波解析表达式为
其傅里叶变换为
ψ(af)=e-π2fb(af-fc)2
式中:fb为带宽参数,fc为中心频率,a为变换尺度。Morlet小波的时间和频率分辨率分别为
式中:fi=fcfs/a,因此可通过调整fc与fb来改变Morlet小波变换的时频分辨率。
在工程应用中,选用不同的小波基分析同一问题时结果可能相差甚远。对单自由度信号,直接使用cmor2-1小波即可。对多自由度信号,可采用“稀疏性”评价标准Shannon熵[11-12]E(fb,fc),评价Morlet小波cmorfb-fc与特征频率成分是否匹配。同时,为了保证小波变换模态解耦的准确性,引入小波脊线对数与拟合直线的标准差σ。
设定最小化目标函数
Jobj=E(fb,fc)+σ
采用序列二次规划法对参数fb和fc进行优化。根据时频分辨率要求,fb和fc须满足约束条件
式中:α表示相邻Morlet窗重叠程度,α越大,模态分离能力越强。β为时间窗倍数,表示小波的有效持续时间,用于消除边端效应。γ用于确保有足够可分析信号长度。研究表明,当α=2、β=4、γ=0.4时,密集模态能完全分离,端点效应能完全消除。经仿真验证,一般迭代次数小于20,参数fb和fc的SQP优化即收敛。

图2 四种阻尼识别方法Fig.2 Four damping identification method
2 单频模态阻尼分析
为评价阻尼识别技术的性能,对单自由度线性阻尼系统进行仿真研究。线性单自由度系统的衰减响应为
y(t)=Ae-ζωntsin(ωdt+φ)
其中,A为系统的初始振幅,ωn为系统固有频率,ωd为阻尼频率,ζ为系统阻尼比,φ为系统振动初始相位。取表1数据进行仿真。

表1 单自由度仿真参数Tab.1 Parameter of a single mode
2.1 频率误差对阻尼识别影响
根据拟合直线斜率和模态阻尼的关系k=-ζωn,频率分析的好坏直接影响阻尼识别结果。尤其是FSMB是根据频率ωn确定富氏级数展开的周期。因此提高频率识别精度十分重要。
为研究频率识别误差对阻尼识别精度的影响,对单频自由衰减信号进行仿真,其真实模态频率为6 Hz,识别频率波动为5~7 Hz,利用本文提出的阻尼识别技术进行分析,得到阻尼识别误差如图 3所示。结果表明频率误差在0.5 Hz范围内阻尼识别误差小于10%,且阻尼识别误差随频率误差增大而增大。如图3所示,FFTMB、FSMB、Hilbert、Wavelet共4种阻尼识别方法的识别误差大小随频率变化基本相当,表明误差主要来源于-ζωn,即从幅值对数曲线中拟合得到的直线斜率,尽管在各个分析频率下识别得到的包络线相当准确。

图3 频率识别误差对阻尼精度影响Fig.3 Effects of error in identified frequency on the identified damping
2.2 噪声影响
噪声在工程数据处理中通常是不可避免的。工程噪声水平通常在5%~10%,为分析噪声对4种阻尼识别方法精确度的影响,在参数如表1的瞬态自由衰减信号中加入高斯白噪声,噪声水平(0% ~ 15%),其中5%噪声水平对应于均值为0、方差为瞬态信号初值5%的正太分布随机信号。对一系列包含噪声的瞬态信号,取0~4 s信号进行分析,阻尼分析值与真实值的误差如图4所示。
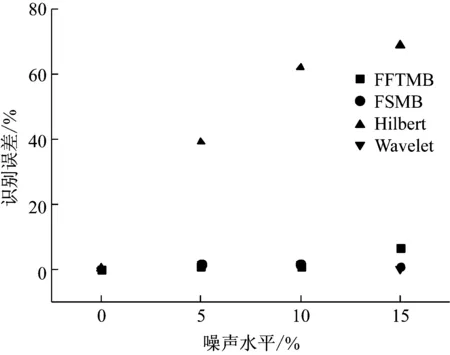
图4 不同噪声水平影响下阻尼识别误差Fig.4 Effects of varied noise level on the identified damping
在2%阻尼比,耦合(5%~15%)噪声影响下,除Hilbert方法外,3种阻尼识别方法分析得到的阻尼识别误差均在7%以下,表明该3种阻尼识别方法具有较强的噪声抑制能力。若信号通过数字滤波器滤去高频噪声,则0%~15%噪声水平下4种阻尼识别方法的识别误差均小于5%。
FFTMB法通过反复作FFT变换得到包络线幅值,FSMB法通过信号的整周期数值积分得到包络线幅值,Wavelet法通过在一定的频率下,计算响应的连续小波变换系数得到包络线幅值,都具有较强的频率分离能力来抑制噪声。因此这3种方法在噪声干扰下得到的幅值包络线仍比较光滑。而Hilbert变换相当于将信号每个时刻点的相位改变90°,信号的幅值不变,因此对噪声没有抑制作用,在噪声影响下识别出的阻尼误差很大。
3 多重临近频率模态阻尼分析
复杂系统如直升机旋翼中测得的信号一般包含多阶模态,当旋转旋翼的摆振模态被激起后,测得的摆振响应信号特点为噪声水平高,lag/rev(摆振频率)被持续的旋翼转速气动力谐波信号破坏。实际上,摆振频率与旋翼1/rev基频相近且小于基频。悬停和地面共振试验时,气动力谐波幅值与摆振幅值相比较小,但前飞时,气动力谐波幅值通常与摆振幅值相当。
基于摆振模态信号的特点,主要考虑两个因素,1阶摆振信号与气动力1/rev谐波的频率差和幅值比对阻尼识别精度的影响。典型的仿真信号如下
y(t)=Ae-ζpωptsin(ωpt+φp)+
Be-ζcωctsin(ωct+φc)
其中ωp为1阶摆振自然频率,ωc为旋翼1/rev频率。A和B分别为其初始幅值,ζp为1阶摆振模态阻尼,ζc为1/rev气动力的阻尼。
为评估幅值比对阻尼识别的影响,设置仿真信号的主模态参数如表1,次模态幅值B在0~5变化、1/rev频率为7.5 Hz(Δf=1.5 Hz),信号长度为4 s。
临近模态幅值比对阻尼识别的影响如图 5所示。在2%阻尼水平,FFTMB和Hilbert法的阻尼识别精度随着幅值比增大而减小,当幅值比大于20%时即不能得到准确的阻尼估计。FSMB和Wavelet法在该工况下可准确识别模态阻尼。
旋翼1阶摆振模态通常在0.3/rev~0.8/rev之间变化,为分析1/rev和lag/rev之间频率差对阻尼识别精度的影响,设置仿真信号的主模态参数如表1,次模态与主模态的频率差Δf在0~0.25/rev变化,1/rev信号幅值B等于1。频率差对阻尼识别精度影响如图 6所示。FFTMB和Hilbert法不适用于该工况。在2%阻尼水平,当Δf大于0.05/rev时FSMB法可准确识别摆振模态阻尼,当Δf大于0.08/rev时Wavelet法阻尼识别结果准确。同时Δf越小,FSMB和Wavelet法的可分析信号长度越短。

图5 模态幅值比对阻尼识别影响Fig.5 Effects of the varied amplitude ratio of a spectrally close mode on the identified damping

图6 模态间频率差对阻尼识别影响Fig.6 Effects of a spectrally close mode with varied frequency on the identified damping
综上所述,在2%阻尼水平,当频率差大于0.2/rev时FSMB和Wavelet法都可准确识别模态阻尼,其阻尼识别结果可互相印证。
4 无轴承旋翼装机条件下的旋翼一阶摆振阻尼识别的应用研究
全尺寸无轴承旋翼装直11型机试验中,直11型机停放在水泥地面,处于无系留自由状态。驾驶员通过顺旋翼旋转方向摇动驾驶杆对自动倾斜器不旋转环施加频率为ω的周期激励,引起旋转坐标系桨叶桨距角产生频率为(Ω+ω)和(Ω-ω)的变化(Ω为1/rev旋翼频率),从而激起相应的气动力,进而激起桨叶的挥舞运动,再由挥舞运动引起的哥氏力激起桨叶的摆振运动。待桨叶运动达到稳态后,突然停止激励。典型试验状态(实测)如表2所示。
试验中,驾驶员根据信号发生器提示按给定频率通过驾驶杆施加激励。采集的固定坐标系和旋转坐标系下典型时域信号:驾驶杆横向位移、尾减Z向过载、柔性梁330剖面摆振弯矩如图7所示。根据驾驶杆横向位移识别得到驾驶杆激励频率估计为1.65 Hz,则传递到桨叶的后退模态(Ω-ω)激励频率为4.517 Hz,即图7桨叶摆振弯矩信号中的稳态激励频率。柔性梁的摆振频率和机身的振动频率表明,通过晃动驾驶杆,激出了旋翼摆振后退型模态。驾驶杆激励停止后,各测点数据呈收敛趋势,因此该工况下不存在地面共振。

表2 试验状态Tab.2 Test condition



图7 摆振模态信号衰减时域曲线Fig.7 Time-domain response of lead-lag mode
截取激励停止后的桨叶和柔性梁摆振自由衰减信号,按图1所示流程分别采用FFTMB、FSMB、Hilbert、Wavelet方法对桨叶和柔性梁各剖面信号进行一阶摆振模态阻尼识别。桨叶650剖面摆振信号、旋翼一阶摆振模态阻尼识别结果如图8所示。从时域图和频谱图中可以看出,初次截取的自由衰减信号中包含谐波和噪声干扰信号,利用带通数字滤波器滤掉干扰信号,再次截取自由衰减信号(截取时间长度接近整周期),采用FFTMB、FSMB、Hilbert、Wavelet方法对识别出的一阶摆振频率估计4.682 Hz进行模态阻尼识别,其等效黏性阻尼识别结果分别为1.934 7%、1.957 2%、1.930 5%和1.940 2%。不通过滤波器,FSMB法和SQP优化得到的小波cmor9.45-0.93阻尼识别结果为1.8963%和1.9046%。根据图 8中FSMB和Wavelet法幅值对数曲线可知,阻尼是弱非线性的。柔性梁和桨叶各剖面的阻尼识别结果如图9所示,所采用的4种阻尼识别方法分析得到的柔性梁和桨叶各剖面阻尼比近似相等,阻尼识别结果可信。
对桨叶一阶摆振模态传递到机身的响应的频率和阻尼进行分析。尾减过载Z向的阻尼识别结果如图10所示,其激励频率估计为1.616 Hz,与桨叶摆振频率4.682 Hz的和为6.298 Hz,约等于桨叶旋转基频6.16 Hz。根据桨叶旋转坐标系→自动倾斜器→机身固定坐标的力传递关系,验证了FFT分析识别出的桨叶一阶摆振频率正确性。

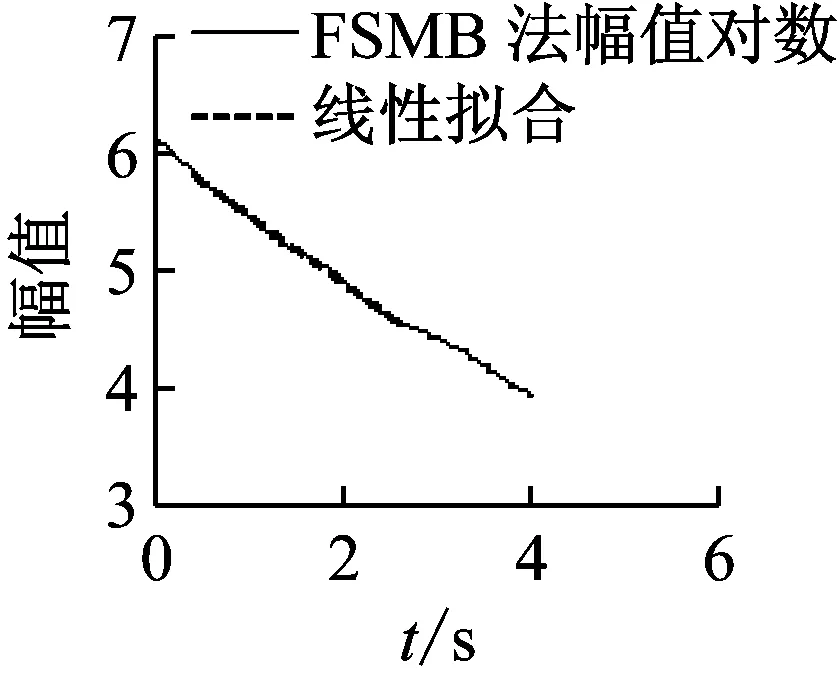


图8 桨叶650剖面一阶摆振模态阻尼比Fig.8 Damping in section 650 of first lead-lag mode

图9 桨叶各剖面一阶摆振模态阻尼比Fig.9 Damping in multiple sections of first lead-lag mode

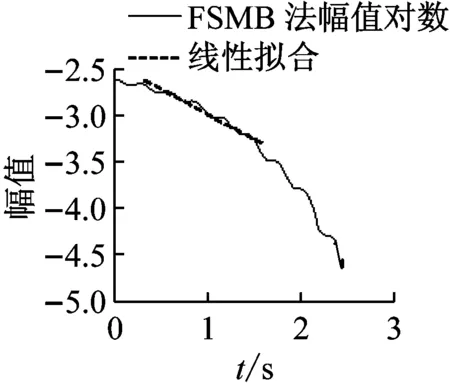
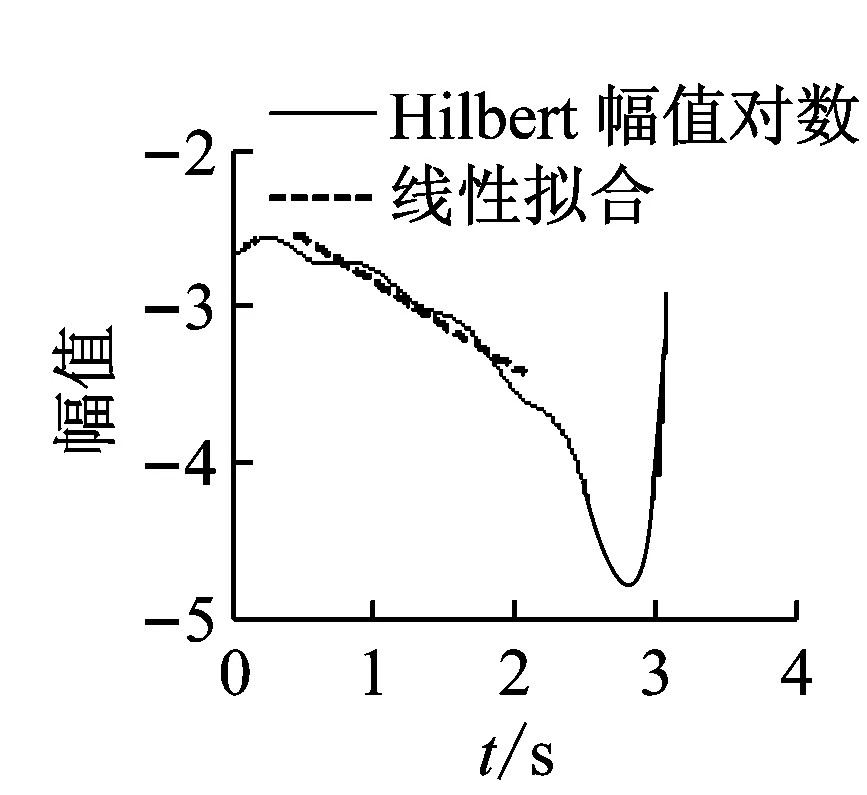
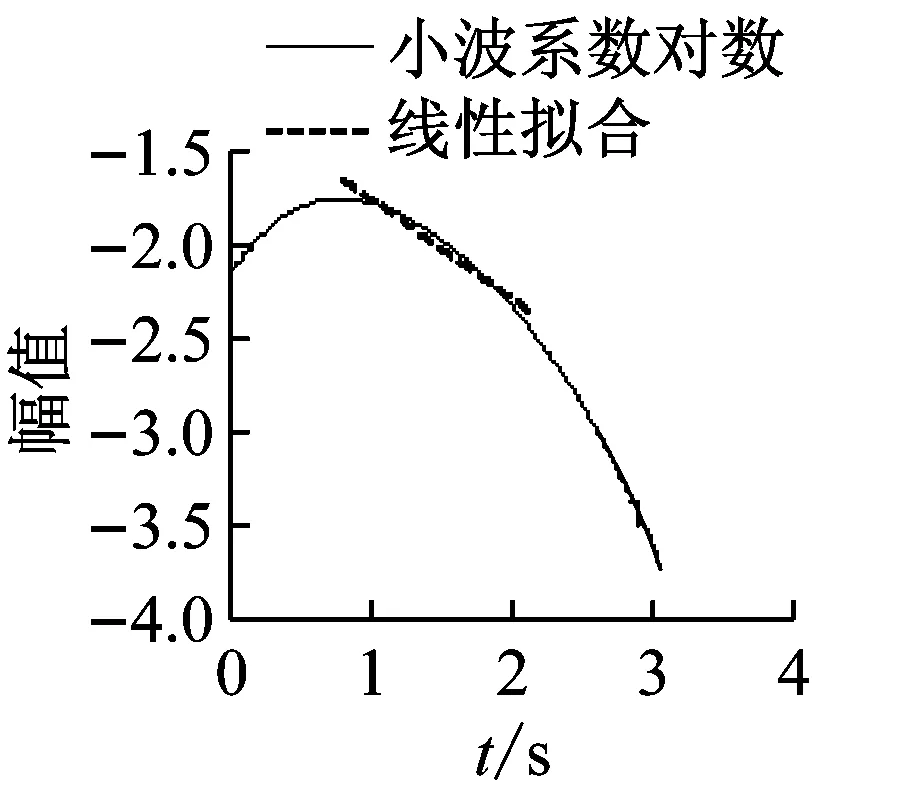
图10 尾减Z向过载摆振响应阻尼比Fig.10 Damping of response result from lead-lag motion in Z axis of tail reduction gearbox
固定坐标系下机身测量点尾减速器过载Z向、副驾驶座椅过载Z向与旋转坐标系下桨叶摆振弯矩信号相对应的1阶摆振模态阻尼衰减系数ζωn(FSMB法)对比结果如表3所示。以柔性梁330剖面的阻尼衰减系数为标准,表中机身测点的阻尼衰减系数与柔性梁的误差均小于6%,验证了本文发展的桨叶一阶摆振模态阻尼识别技术。

表3 机体与桨叶摆振模态阻尼(FSMB)比较Tab.3 Lead-lag modal damping of fuselage and blade
5 结 论
本文系统研究了模态阻尼识别FFTMB、FSMB、Hilbert和Wavelet法,进行了参数影响仿真分析,发展了根据自由衰减时域信号识别旋翼摆振模态阻尼的技术,并完成了基于全尺寸无轴承旋翼装机地面共振试验的旋翼一阶摆振模态阻尼识别研究,得到以下结论:
(1) 基于SQP的小波中心频率和带宽优化选择方法可有效分离小阻尼比条件下高幅值比、密集模态,准确识别无轴承旋翼地面共振试验的摆振模态阻尼。
(2) FFTMB、FSMB和Wavelet阻尼识别方法噪声抑制能力较强,Hilbert法没有噪声抑制能力,不适合用于低信噪比情形;FSMB和Wavelet法密集模态阻尼识别能力较强,其阻尼识别试验分析结果相近。
(3) 数值仿真及试验实分析结果表明,本文发展的阻尼识别技术能有效识别无轴承旋翼摆振模态阻尼。
