基于参考臂低频相位调制的微弱振动光学相干检测

2018-10-19张烈山张晓琳唐文彦

振动与冲击 2018年19期

张烈山，张晓琳，刘刚，唐文彦

(1.哈尔滨工业大学电气工程及自动化学院，哈尔滨 150001；2.上海卫星工程研究所，上海 200240)

振动是自然界物体最主要的运动形式之一，它广泛存在于生产生活中的各个方面，例如人类发声时的声带振动和声传播时的介质振动、昆虫飞行中翅膀的振动，地震时的大地振动，装备制造车间各种机床的振动，交通运输领域中桥梁和铁路等设施的振动，建筑行业中高层建筑的晃动，船舶、飞行器等发动机的振动、空调压缩机的振动等等[1-5]。可见，振动测试的研究具有非常重要的现实意义。

随着微纳加工技术的飞速发展，人们越来越关注高频微小振动的测试，尤其是在航空航天、半导体制作等工程领域，高频微弱振动的检测技术已成为研究热点之一[6-7]。包括激光相干[8]、光纤传感[9]在内的光学技术手段是实现微弱振动检测的主要方法，其中尤以激光多普勒相干技术为代表，多普勒相干检测技术具有检测范围大、测量精度高等优点，是学者们研究最多的一种振动检测技术。根据不同的光路结构和调制解调机理，多普勒相干法微弱振动检测技术主要可以分为：单频干涉测量法、双频干涉测量法[10]、正弦相位调制干涉测量法[11]、正交偏振干涉测量法[12-13]、激光自混合干涉法[14]等。以往的研究中，通常对相干测振信号进行相位解调来实现各个振动参数的估计，然而有时被测振动的振幅极为微弱，并且常常淹没在大幅度环境扰动中，这种情况下无论采用那种探测结构都难以获得稳定的相干信号，微弱振动对相干信号的调制深度本身就比较浅，因此利用解相的方法来实现微弱振动参数的估计仍然显得非常困难。本文在激光多普勒相干技术的基础上，针对这种微弱振动参数的检测问题进行了研究，提出了一种全新的思路，在干涉光路的参考臂增加低频相位调制，再利用频谱分析来实现纳米级中高频微弱振动的参数估计，重点对这种微弱振动的振幅进行检测分析。

1 基本原理

一般地，激光多普勒相干检测方法都是通过测量臂接受被测振动的相位或频率调制然后与参考臂进行干涉，从干涉信号的频谱、相位、时频分布或瞬时频率等特征中提取出被测振动的相关信息。对于振幅仅有纳米量级的微弱振动，它对激光的频率调制作用是难以捕捉到的，通过频率解调通常无法提取出所关心的信息；它对激光束的相位调制深度也很浅，还常常淹没在环境的扰动中。因此，常规方法实现纳米量级的相干检测是很有难度的。

1.1 参考臂低频调制相干检测原理

由于纳米级微弱振动对激光束的调制深度非常浅，根据单频激光干涉法的基本原理，如果不预先对相干系统进行内调制或外调制，探测系统无法获得包含振动信息的交变探测信号。通常利用声光调制或电光调制等手段使激光束实现光频或相位的调制，再对微弱振动进行相干检测，这些方法或使参考臂和测量臂两束激光产生高频差，或者使参考臂生成高频相位载波。完全不同于以往的光学相干系统，本文提出了一种在参考臂增加低频相位调制的相干检测系统，其原理示意图如图1所示。

图1 参考臂低频调制的激光相干检测系统示意图Fig.1 Diagram of coherence detection system with reference arm low-frequency modulated

假设在参考臂增加了一个振幅为Am(典型值：2 μm)，角频率为ωm(典型值：10π rad/s)的正弦调制信号，并假设待测微弱振动为一个振幅为As，角频率为ωs的简谐振动(其他类型可分解为简谐振动的叠加)，忽略调制源和被测振动的初相位，并且忽略相干信号的直流分量和高频分量(光电探测器对高频分量的响应为一个直流信号)，那么相干探测信号可由下式表示

U(t)=Acos[2k(Amsinωmt+Assinωst)+Ø0]

(1)

式中:A为系统增益，它由两束激光的强度以及光电转换效率等因素决定;Ø0表示由相干光路初始光程差以及环境扰动等因素造成的相位;k表示激光束的波数。由式(1)可知，相干探测信号的相位中包含了待测振动的振幅及频率信息，通过进一步处理可以提取出待测振动振幅和频率信息。

1.2 微弱振动参数的解调

利用三角函数的和差化积公式及贝塞尔恒等式

(2)

式中:n为整数，Jn(β)表示β的第n阶贝塞尔函数值，将式(1)所示信号分解为ωm和ωs的整数倍谐波项以及它们的和频项及差频项之和，记xm=2kAm、xs=2kAs，由于分解出来的项次很多，这里用表1给出信号分解结果中各个频率分量的幅值，由于对于纳米量级的微弱振动，它对干涉信号的调制深度xs非常浅，其二阶以上贝塞尔函数Jn(xs)的值已经趋近于0，因此，可以忽略信号中的高频分量。

表1微弱振动相干探测信号各频率分量的幅值
Tab.1Frequenciesandamplitudesofcomponentsintheweakvibrationcoherencedetectionsignal

序号角频率/(rad·s-1)幅值/V10Acos(Ø0)J0(xs)J0(xm)2(2n+1)ωm2Asin(Ø0)J0(xs)J2n+1(xm)32nωm2Acos(Ø0)J0(xs)J2n(xm)4(2n+1)ωm+ωs2Acos(Ø0)J1(xs)J2n+1(xm)5-(2n+1)ωm+ωs2Acos(Ø0)J1(xs)J2n+1(xm)6ωs2Asin(Ø0)J1(xs)J0(xm)72nωm+ωs2Asin(Ø0)J1(xs)J2n(xm)8-2nωm+ωs2Asin(Ø0)J1(xs)J2n(xm)

观察表1各频率分量的幅值，不难总结出相干测振信号的频谱分布规律。

(1)信号中有直流分量，其幅值为Acos(Ø0)J0(xs)J0(xm)，也即由系统增益、初始相位以及被测振动振幅、参考臂调制信号振幅来决定，实践中在采集相干信号时进行了隔直滤波，因此，实测信号中直流分量的幅值不一定与理论值相符；

(2)信号的低频段出现了密集分布的谱线，它们由参考臂低频调制信号频率的奇数倍频率分量(2n+1)ωm及偶数倍频率分量2nωm构成；

(3)信号的中高频段出现了密集的谱线分布，谱线的整体幅值比信号的低频段谱线幅值明显要小，它们由以下频率分量构成：ωs分量、ωs±(2n+1)ωm分量、ωs±2nωm分量，这个信号谱线分布带以微弱振动频率ωs为中心。

根据测振信号的频谱分布规律，可以通过提取中高频段谱线分布带的中心频率来实现微弱振动的频率识别。从表1中，观察到(2n+1)ωm分量的幅值为2Asin(Ø0)J0(xs)J2n+1(xm)，再经过ωs频移后，(2n+1)ωm+ωs分量的幅值变为2Acos(Ø0)J1(xs)J2n+1(xm)，两者的比值为tan(Ø0)J0(xs)/J1(xs)，记这一比值为Ro，当初始相位Ø0能够被测定时，根据这一比值可以反求出调制度xs的值，进而得到微弱振动的振幅As；同样的，还能观察到2nωm分量的幅值与2nωm+ωs分量的幅值之比为cot(Ø0)J0(xs)/J1(xs)，记这一比值为Re，定义衰减比R为

(3)

这样不必精确测定初始相位Ø0也能通过各频率分量频移前后的幅值反求出调制度xs的值。衰减比越大说明低频分量在平移ωs后振幅衰减程度越大。相干测振信号的频谱分布容易通过傅里叶变换来得到，因此，可在频谱分析的基础上计算出衰减比R。为了减小衰减比R计算的随机误差，可以采用多个频率分量振幅信息来计算比值Ro和比值Re，也即利用低频段所有有效频率分量的振幅以及它们频移ωs后的分量幅值

(4)

这样几乎利用了全部频率分量的信息，显著提高衰减比R的计算重复性。

2 仿真研究

对前面所述的微弱振动检测方法进行数值仿真研究，假设探测系统激光的工作波长为632.8 nm，系统的增益系数A为1，初始相位为0.15π；假设被测振动的振幅为15 nm，振动频率为2 kHz；并假设在相干系统的参考臂增加的低频调制的振幅为2 μm，频率为5 Hz。根据式(1)可获得仿真信号，如图2所示。图中虚线表示归一化后的参考臂低频调制信号。

图2 频率为2 kHz微弱振动仿真探测信号Fig.2 Simulation detection signal of 2 kHz weak vibration

2.1 仿真信号被测振动参数的解调

对图2所示仿真信号进行频谱分析，可得信号的频谱分布如图3所示，由图3可知信号的频谱分布与前述分析的完全一致，在被测振动频率2 kHz附近出现了密集的谱线分布，这一信号频带的中心频率为2 kHz，可根据这一特征通过设定频谱阈值提取信号频带、再计算信号频谱带的中心频率来获得被测振动的频率。

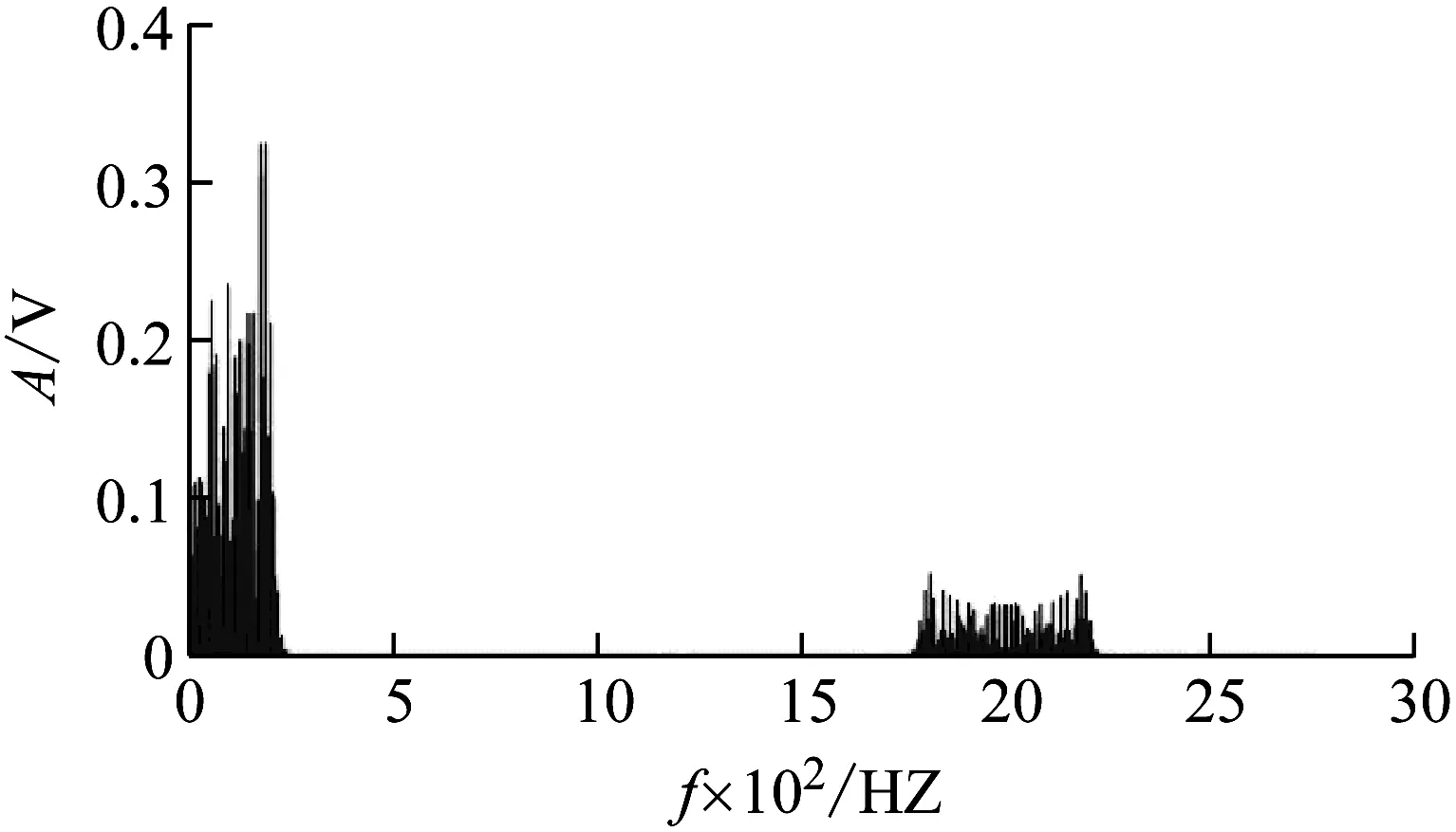
图3 仿真信号的频谱分布Fig.3 Fourier spectrum of the simulation signal

根据仿真信号的频谱分布可知，信号的低频段宽度约为250 Hz(也即中频段信号频带的半宽)，根据表1序号为2、3的低频分量幅值表达式可知，对于低频段信号频谱的大小主要由参考臂调制深度的贝塞尔函数值Jn(xm)来决定，随着阶次n的提高，调制度2kAm的贝塞尔值趋近于0，探测光波长为632.8 nm的情况下，调制度的贝塞尔函数Jn(2kAm)与函数阶次、低频调制源的振幅之间的关系如4所示。由图4可知，对于低频调制源振幅为2 μm的情况，Jn(2kAm)的值约在阶次n=50之后变为0，结合低频调制源的频率5 Hz，即可知相干信号的低频段长度约为250 Hz。在设置参考臂低频调制源的参数时，必须综合考虑频率和振幅两个参数，理论上其频率越低越好，在频率选定后，调制源的振幅不能太大也不能太小，大振幅使得相干信号的低频段谱线分布带宽过大覆盖了被测振动频率；小振幅使相干信号中有效的低频分量个数太少，进而使得计算各个分量振幅之和时产生较大的随机误差。

图4 低频调制深度的各阶贝塞尔函数Fig.4 Different orders’ Bessel function values of the low-frequency modulation depths

由频谱分布可观察到信号中ωm的奇数倍频率的分量个数约为25，计算这25个低频分量的幅值之和等于1.952 6，这25个低频分量经过ωs频移后幅值之和为0.577 2，那么可计算出Ro等于3.383 0；同样的计算出25个ωm的偶数倍频率的分量幅值之和等于3.418 2，这些分量经过ωs频移后幅值之和等于0.262 3，那么可计算出Re等于13.030 7；于是根据式(3)可计算出衰减比R为6.639 5。由式(3)可知衰减比R与调制深度2kAs有着明确的函数关系，由于式(3)所说的函数在一定区间内反函数难以求解，工程中可采用查表法得到As的值，利用查表法可得调制深度2kAs约等于0.297 9，对应被测微弱振动的振幅为15.00 nm，这与预先设定的参数值完全一致，证明了本文所提出方法的正确性。

2.2 振幅检测方法的抗噪性

衰减比R与被测振动振幅As的函数关系如图5所示，由图可知被测振动幅度越小，衰减比R越大，低频信号分量经过ωs频移后信号的幅值变得非常小，因此在计算频移分量的幅值之和时重复性较差，导致R值的计算重复性较差，然而根据图中这一部分曲线的曲率可知，在反求被测振动的振幅As时，仍然具有很好的测量重复性；被测振幅越大，衰减比R越小，低频信号分量经过ωs频移后信号的幅值仍然具有较大的幅值，这使得R值计算具有较好的重复性，这样也就保证了振幅As的测量重复性。利用该方法测量被测振动的振幅，其振幅检测上限约为150 nm，超过该值时式(3)函数不存在反函数，也即1个R值可能对应多个调制深度xm值。

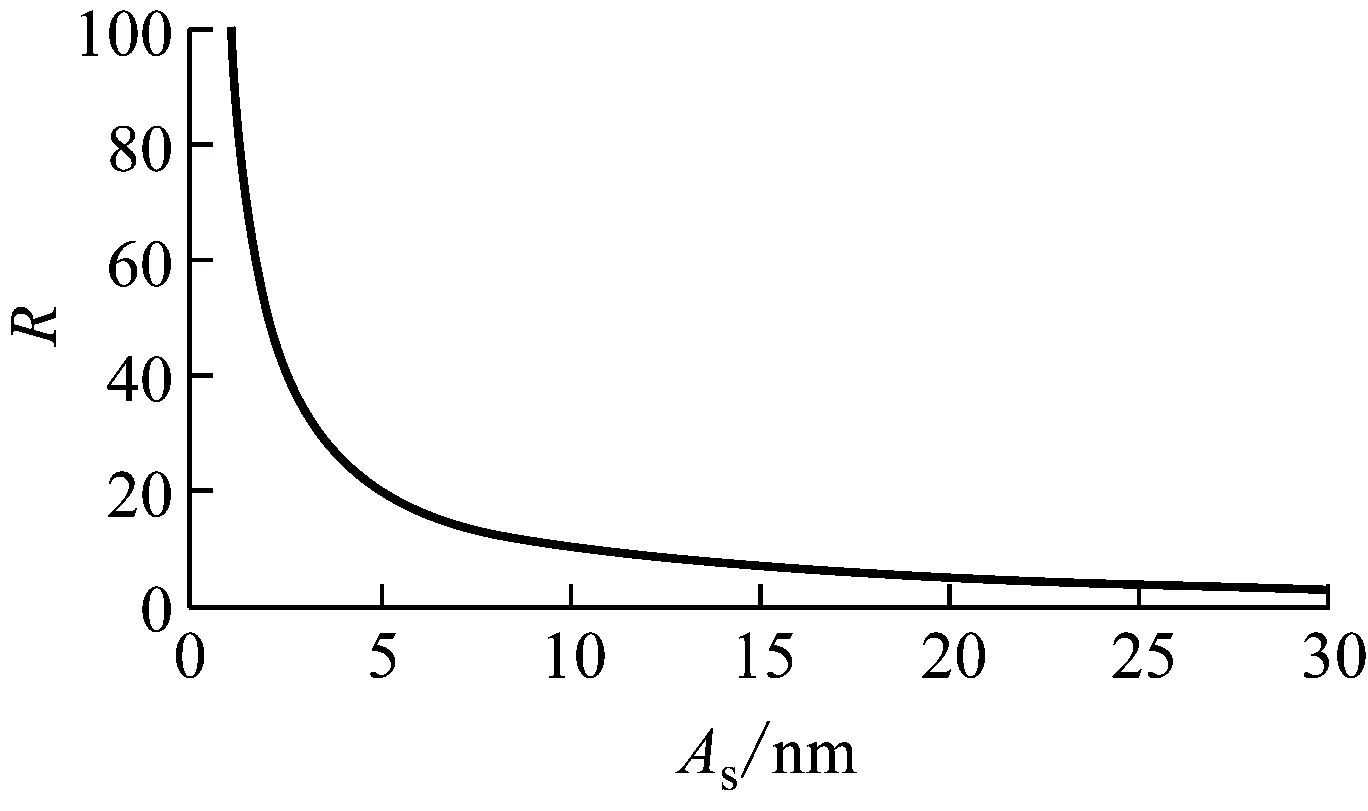
图5 被测振幅与衰减比R的关系曲线(激光波长632.8 nm)Fig.5 Relationship curve of the detected amplitudes versus attenuation ratio R at laser wavelength of 632.8 nm

由于在计算衰减比R时进行了多个频率分量幅值的累加，这样的操作很好地抵消了白噪声的影响，对于仿真信号的处理，再计算Ro和Re时，即使只采用了25个频率分量的信息，仍然取得不错的抑制噪声的能力。表2所示为，在仿真信号中加入不同信噪比的高斯白噪声后，被测振幅的计算结果。由表2可知，随着信噪比的降低，振幅解算的误差也越大，但即使信噪比低至4 dB，振幅解算的误差也不到1 nm，本文所述的方法表现出较强的抗噪特性。

表2 不同信噪比条件下被测振幅的解算结果Tab.2 Caculation results of vibration amplitudes under

2.3 振幅检测方法的抗干扰能力

工程实践中，干涉信号的相位中常常含有低频随机的环境扰动，本文所述的方法对环境的随机扰动还具有一定的抵抗能力。假设某一时刻相干探测信号中的包含以下几种随机扰动：它们的角频率为ωi，ωj，…，ωk，它们的振幅分别为Ai，Aj，…，Ak，也即对相干信号的调制深度为xi，xj，…，xk，那么可通过信号分解可知，忽略初始相位及增益系数的影响，那么相干信号中角频率为(nωm+mωi+pωi+…+qωk)分量幅值为2J0(xs)Jn(xm) Jm(xi) Jp(xj)…Jq(xk)，该分量经过ωs频移后，幅值变为2J1(xs)Jn(xm) Jm(xi) Jp(xj)…Jq(xk)，于是在求比值Ro或Re时，可以将无关的乘积项消除，式(3)的关系仍然成立。

这些扰动在时间上具有随机性，无论何时出现环境扰动，这些环境扰动经待测的中高频振动的移频作用后，幅值都会呈现有规律的衰减，而傅里叶变换是一种全局变换，最终会在信号的频谱中反应出来，再做幅值之和的比值时又将换算系数(局部信号的傅里叶频谱幅值与其实际幅值存在比例换算)消除了，因此仍然能够保证式(3)成立。对此也进行了仿真研究，在信号的前半段时间内加入频率为2π rad/s、振幅为1 200 nm的环境扰动，在信号的后半段时间则加入频率为4π rad/s、振幅为1 400 nm的环境扰动，最终解调出被测振动的振幅为14.879 2 nm，这说明本文所述的方法仍然保持了较高的检测精度。

3 实验方案

为了验证前文所述方法对微弱振动探测的可行性，如图6所示为一套用于探测水下声源激发的水表面波的激光相干探测系统，水下声源激发的水表面波[15-16]是一种振幅在纳米量级的微弱振动。

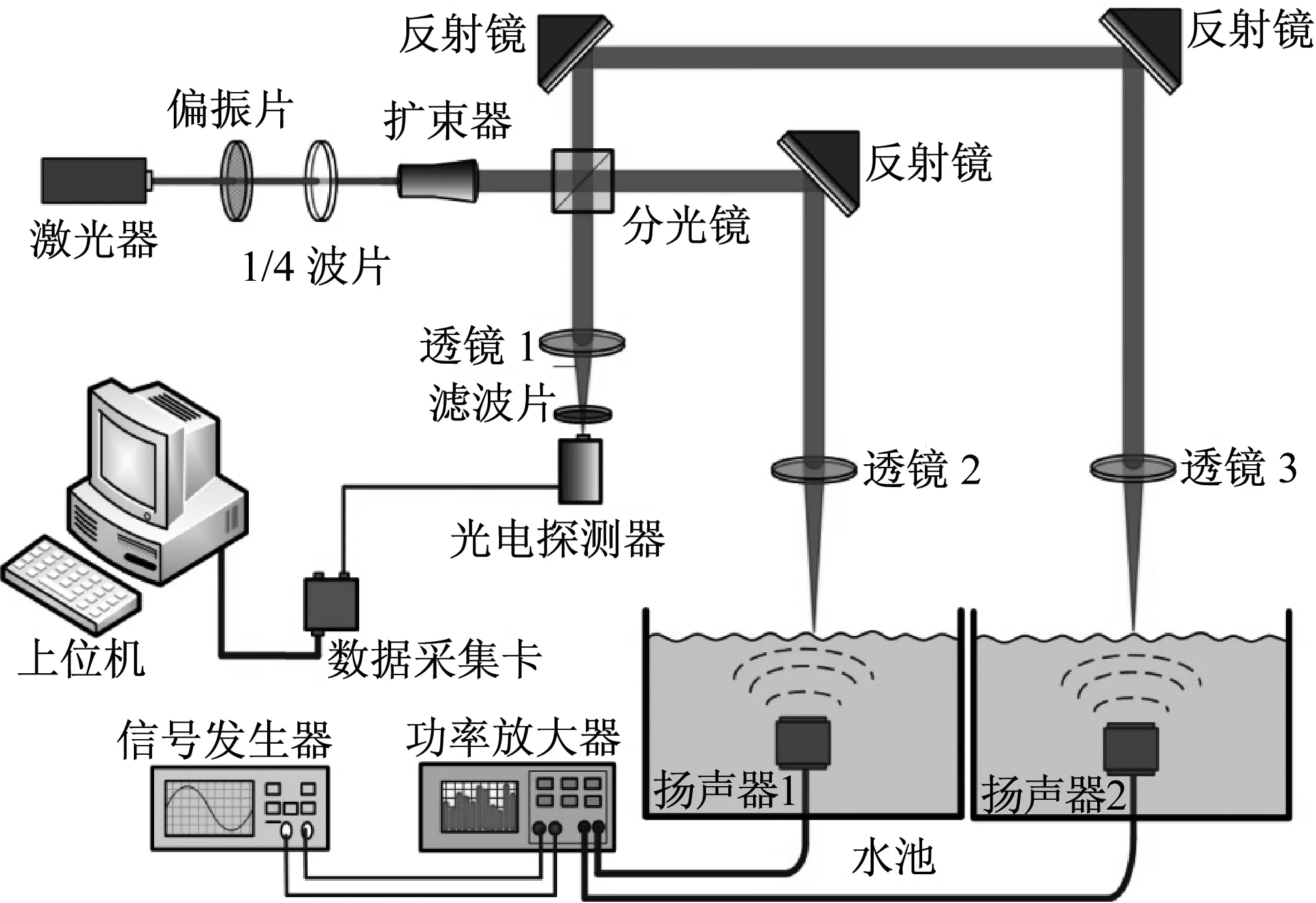
图6 中高频纳米级微弱振动的相干检测实验系统Fig.6 Coherence detection experimental system for medium-high frequency nanometer vibrations

探测的系统可以分为三大模块：①被测振源及参考臂低频调制源激发模块，在这个模块中，信号发生器输出特定频率的电信号经过功率放大器后驱动水下扬声器，水下扬声器发声后激发了水表面的同频振动，以水下声源激发的水表面波作为被测振源，并且同样采用水下声源激发水表面波的方式获得参考臂调制源，这样做的优点在于以非常低的成本获得调制源，而且可以使相干光路系统获得光强相当的测量光和参考光，使系统获得较高的干涉条纹对比度，实际探测中低频调制源的频率为5 Hz(虽然不在水下扬声器的最佳响应范围内，但仍有响应输出)；②激光相干检测模块，采用工作波长为632.8 nm的He-Ne光源，光源输出的激光束经过偏振片和1/4波片后通过扩束器准直和扩束作用，再经过分光镜后分为两束激光：参考光和测量光，测量光和参考光分别经过反射镜和定焦透镜后被聚焦到水表面上，测量光的相位被待测振动(水表面波)所调制，参考光则也被低频水表面波调制，受到相位调制后两束激光回到光路系统，在经过分光镜后两束汇合发生了干涉现象，经过透镜和滤波片后干涉系统被光电探测器接收；③信号采集处理模块：经过光电探测器转换后的相干信号利用数据采集卡传送到上位机做进一步的处理，数据采集采用交流耦合方式与光电探测器相接，直接滤除了干涉信号中的直流分量。

实验系统的主要器件的性能指标参数如表3所示。

4 实验结果分析

利用图6所示探测系统对振动频率为2 kHz的微弱水表面波进行探测实验，参考源的调制频率为5 Hz，其振幅约为7 μm，如图7所示即为实测2 kHz微弱水表面波探测信号的时域和频域分布图，由其频域分布可知，实测信号低频段的带宽约为650 Hz，中频段出现了以2 kHz为中心的信号频谱带，根据这一特征通过设定频谱阈值再计算频带中心的方法计算出微弱水表面波的振动频率，然后根据振动频率和信号频谱分布计算出微弱水表面波的振幅，图示信号处理结果：衰减比R等于4.623 5，振幅As等于21.292 0 nm。

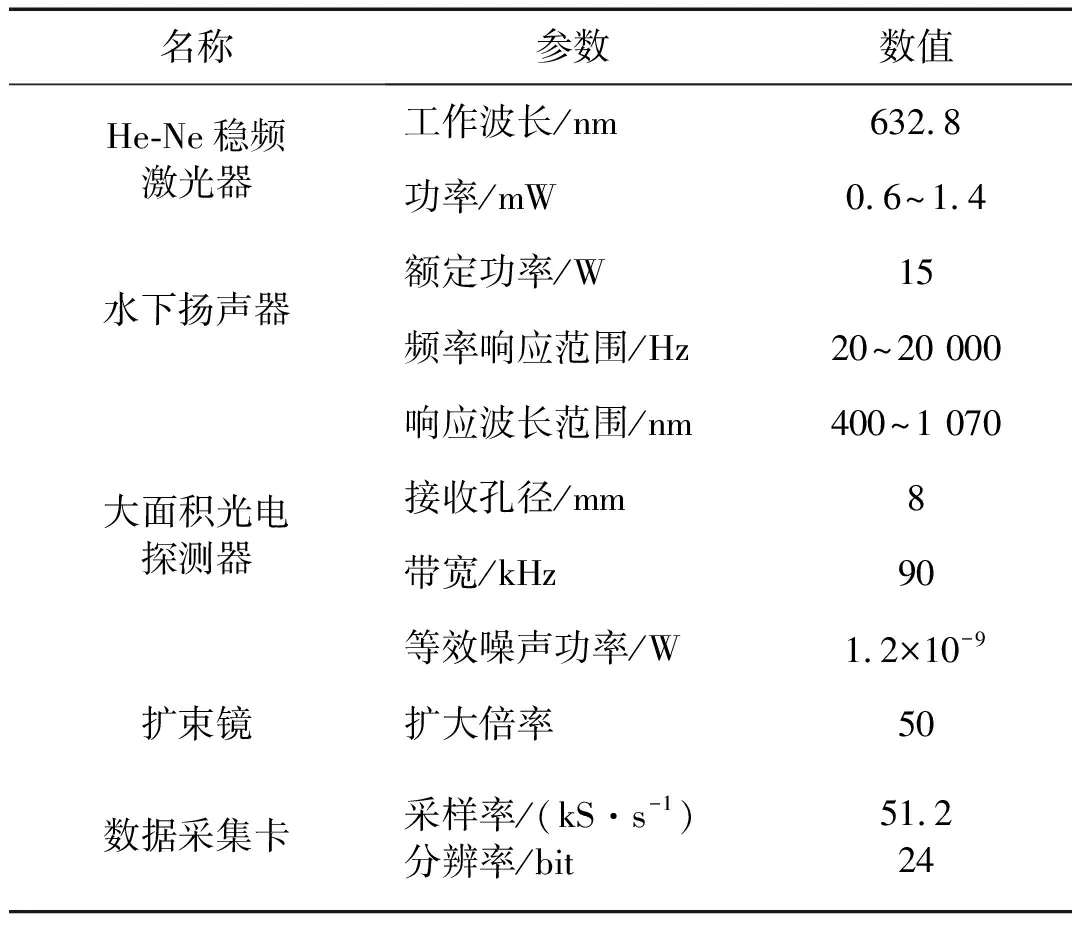
表3 实验系统主要器件的性能指标参数Tab.3 Specification parameters of experimental

图7 实测微弱水表面波相干探测信号Fig.7 The actual detection signal of weak water surface wave

利用探测系统对2 kHz微弱水表面波进行了8次重复性实验，对水表面波的频率和振幅进行解算，实验的结果如表4所示。系统数据采集模块的采样率为51.2 kS/s，采样长度为1 s，也即信号做傅里叶变换的频率分辨率为1 Hz，由表3可知，频率的测量重复性(1倍标准差)为1.04 Hz，也即约为1个频率分辨率。微弱振动振幅的测量重复性1倍标准差)为0.35 nm，可见文本所提出的检测方法对微弱振动振幅的检测具有很高的测量重复性。

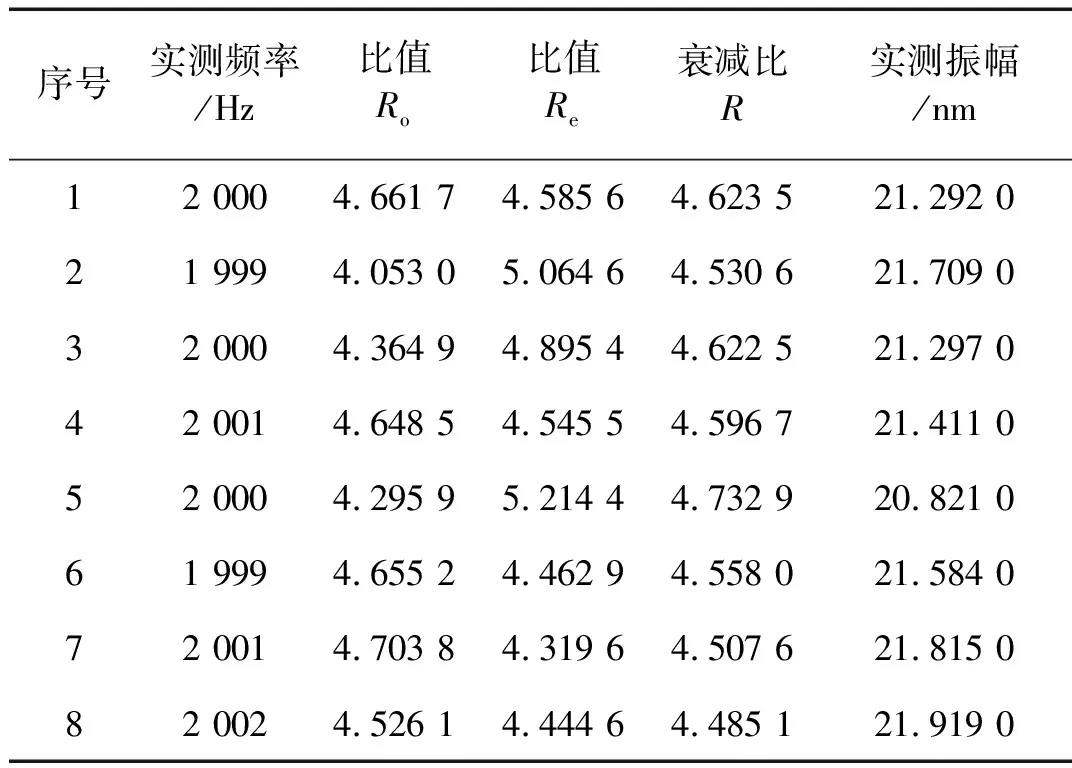
表4 频率为2 kHz的微弱水表面波参数相干检测结果Tab.4 Detection results of 2 kHz weak water surface wave

由于实验室条件的限制，无法获得振幅已知的标准振动源，无法对文章所提的方法进行振幅检测的正确性实验。尽管如此，前述实验已经证明本文所提出的参考臂低频相位调制的相干检测方法对微弱振动的检测是非常有效的，对振幅检测的测量重复高达0.35 nm，待条件具备，可利用标准振动源对该方法进行校准，消除该方法的系统误差。忽略系统误差，以2倍测量标准差来评价本方法的测量精度，那么本文所述的微弱振动振幅检测方法的测量精度为0.70 nm。

前述理论研究和实验分析可知，影响本文所述方法测量精度的因素主要有：①由探测器噪声、环境扰动等随机因素引起的随机误差；②由激光器频率稳定性、功率稳定性因素等引起的随机误差；③低频调制源频率稳定性引起的随机误差。此外，理论上低频调制源的频率越小，在计算衰减比R时可提取到有效频谱分量就越多，计算出微弱振动的振幅时，重复性也就越高。因此工程中，条件允许的情况下，应该时参考臂调制源的频率尽可能低。由于调制深度过浅，对于振动幅度极其微弱的机械振动，传统的激光相干方法无法实现其振幅的检测。显著区别于传统的激光相干检测方法，本文所述方法创造性地在相干系统的参考臂增加了低频调制，通过频谱分析及低频调制信息实现中高频极微弱(纳米级)振动振幅的检测，并且取得了较高的测量精度和抗干扰性能。