一种改进的鱼眼镜头图像矫正算法

隆振海 成都理工大学信息科学与技术学院

1.概述

鱼眼镜头指视角接近或等于180°的镜头。这类镜头一般焦距极短，在135底片格式下，16毫米或焦距更短的镜头通常即可认为是鱼眼镜头，绝大部分的鱼眼镜头均是定焦镜头，只有少部分是变焦镜头。依成像可分为圆形鱼眼（Circular fisheye，又称全周鱼眼，画面呈圆形）与对角线鱼眼（Diagonal fisheye或Full-frame fisheye，画面呈方形）其镜面似鱼眼向外凸出，所视的景物，像鱼由水中看水面的效果。鱼眼镜头一般用来拍摄广阔的风景或于室内拍摄。不少摄影师喜欢使用鱼眼镜的夸张变形来营造透视感。历史上，135画幅最广的鱼眼镜头是艺康旗下的6毫米f/2.8，视角接近220°。而富士能研发了世界首台用于五百万像素CCD摄像机的185°广角全方位镜头鱼眼图像的畸变矫正一直都是今年来的热点问题，其中的代表性方法是球面透视投影矫正法该方法使用球形的投影面用于矫正鱼眼图像，以此为基础的衍生或改进方法还有许多。

OpenCV中已经集成了一种基于球形投影面的鱼眼镜头矫正算法函数，有需要的用户只需要直接调用函数即可。但实际上，由于OpenCV的实现所依赖的公式的局限性，其函数不能处理视角大于180度的鱼眼镜头所提供的图像。

在OpenCV提供函数的基础上，本文提出了一种改进算法，该算法可以对视角大于180°的鱼眼镜头图像进行高效处理且得到准确的矫正结果。

2.OpenCV算法

在OpenCV4.0预览版的算法文档中，可以看到OpenCV对其使用的鱼眼镜头图像矫正算法的细节描述。该算法首先将图像平铺在球心为原点的半球面上，矫正视点O位于原点；此时对于图像上的每一个点P，都有一个三维坐标；定义点P的a，b值分别为a=x/z，b=y/z；其中x、y、z为点P的三维坐标值；定义r = a * a + b * b；定义θ = atan(r)；使用公式θd=θ(1+k1θ2+k2θ4+k3θ6+k4θ8)对θ进行矫正，其后可以得出P点矫正后的位置为x’，y’,其值为x′=(θd/r)a y′=(θd/r)b，如图 2-1 所示。

由该定义可见，OpenCV的做法上是以半球面与z轴的交点为中心O‘，将球面上的点P按照与O’的球面距离展开在平面上，同时对距离进行矫正从而获得矫正图像的效果。如图2-2所示，P为球面上一点，P‘为P点矫正后的位置，以点O’为圆心的圆即为半球面上图像矫正后范围，由于使用了反正切函数，该方法并不能正确处理另外半球的图像。

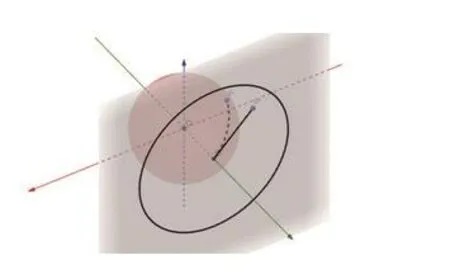
图2 -2 OpenCV算法原理示意图

3.基于OpenCV算法的改进

OpenCV算法使用了反正切函数以求得弧对应角度，从而求取弧长。但在具体实现上，OpenCV使用了反正切函数来求取弧PO‘的长度。反正切函数是一种反三角函数，是利用已知直角三角形的对边和邻边这两条直角边的比值求出其夹角大小的函数，是一种基本特殊函数（Wiki）。在三角学中，反正切被定义为一个角度，也就是正切值的反函数，由于正切函数在实数上不具有一一对应的关系，所以不存在反函数，但可以限制其定义域。因此，反正切是单射和满射也是可逆的，但不同于，反正弦和反余弦，由于限制正切函数的定义域在[-π/2，π/2]，其值域是全体实数，因此可以得到反函数的定义域也是全体实数。

故而当弧PO’对应的圆心角大于90度，即此时需要对视角超过180度的图像进行矫正时，反正切函数将不能得出准确的值。因而，这种方法也不能用于矫正视角超过180度的鱼眼镜头图像。为此，本文提出利用极坐标计算弧对应的圆心角，避免反正切函数的使用，从而将矫正范围从[-π/2，π/2]扩大到[-π, π]（如图3-1所示）。

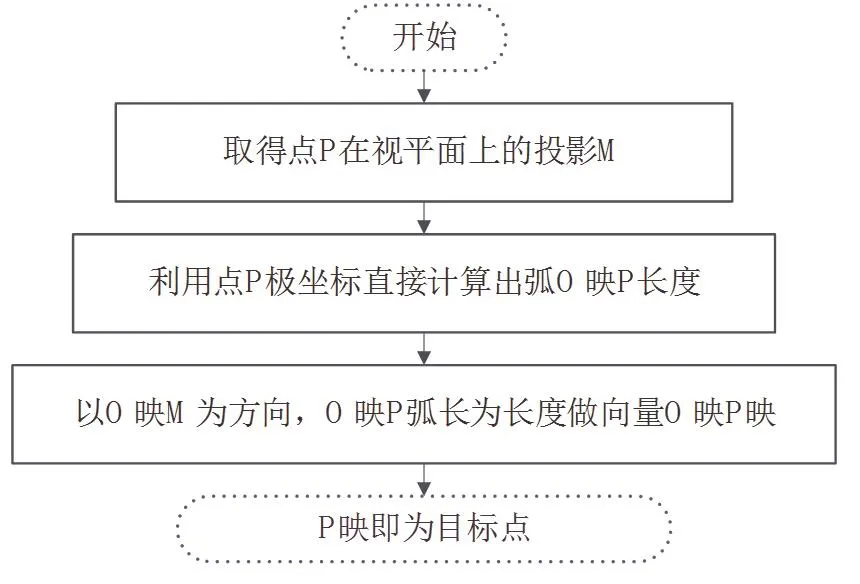
图3 -1 改进算法流程图

4.结论

OpenCV中已经集成了一种基于球形投影面的鱼眼镜头矫正算法函数，有需要的用户只需要直接调用函数即可。但在具体实现上，OpenCV使用了反正切函数来求取弧PO‘的长度。由于限制正切函数的定义域在[-π/2，π/2]，这种方法并不适用于矫正视角超过180度的鱼眼镜头图像。本文提出一种改进的鱼眼镜头图像矫正算法，利用像素点在球面上的极坐标直接计算出弧长，避免了正切函数的使用，从而将矫正范围从[-π/2，π/2]扩大到[-π, π]。