连续宽带钢热浸镀锌生产线锌锅段带钢抖动特性分析

(马鞍山钢铁股份有限公司 安徽 马鞍山 243000)

概述

连续宽带钢热镀锌生产线锌锅段的设备包括：锌锅、沉没辊、纠正辊、稳定辊、气刀装置、合金化炉、合金化炉保温段、气垫风机、冷却风箱、塔顶辊、冷却塔等等。出锌锅段的带钢是由沉没辊、纠正辊、稳定辊和塔顶辊四个辊子支承，一般的连续宽带钢热镀锌生产线冷却塔的高度在40-70米之间，带钢的宽度一般在800-2000mm，两者之比超过40倍，而且上行的带钢中间没有任何支承，运行中的带钢容易发生抖动、扭转等特征，影响到气刀位置处的带钢与喷嘴之间的距离，造成镀层控制的不精确和操作的困难。因此有必要定性和定量分析这段带钢的运行特性。

一、冷却塔上行段带钢的动力学模型

出锌锅段带钢可以表示成图1的支承结构。

考虑重力影响时出锌锅段带钢弦线模型的理论分析。

由于研究的直接对象是塔顶辊与稳定辊之间的带钢，因此可以将沉没辊-纠正辊-稳定辊组成的复合支承系统看成一个简支点，又由于锌锅段带钢的长度远远大于宽度，因此可以用弦模型来研究锌锅段带钢。这样冷却塔上行段带钢可以简化成图2所示的、竖直放置的两端简支轴向运动弦线形式。

图1 上行段带钢的支承结构示意图

图2 竖直放置的轴向运动带模型

图2 微单元

(一)带钢抖动的动力学微分方程

如图3所示，弦上的微元长度为ds；p(x,t)为作用在带横向上的分布载荷；T为张力，有

(1)

其中

v——带钢的轴向运动速度

l——带钢的长度

A——带钢的横截面积

Ρ——带钢的密度

w(x,t)——带钢横向的位移

由式(1)可得

(2)

在作微小振动时，可以作如下近似处理：

(3)

根据牛顿第二定律，无阻尼带钢微元的运动方程：

(4)

式(1)、式(2)和式(3)代入、展开并简化后：

(5)

另外

(6)

所以(5)有如下形式：

(7)

简化后，就可以得到重力场中竖直放置的两端简支轴向运动弦线的动力学方程：

(8)

边界条件为w(0,t)=w(l,t)=0。

(二)动力学微分方程无量纲化

为方便以后的求解和分析，引入如下新的无量纲变量

(9)

(10)

将式(9)和式(10)代入式(8)，并去掉无量纲变量的上角标*号，可得动力学方程的无量纲形式

(11)

边界条件为w(0,t)=w(1,t)=0。

(三)动力学方程简化和求解

(12)

上式的解具有分离变量形式

w(x,t)=ψ(x)eλt

(13)

其中λ=iω

式(13)代入式(12)，其齐次形式

(14)

边界条件为ψ(0)=ψ(1)=0。令

(15)

(16)

(17)

则方程(14)可化为

(18)

边界条件为

ψ(ξ0)=ψ(ξ1)=0

(19)

式(18)是零阶贝塞耳方程，且如式(15)所示，在x区间[0,1]内ξ≠0，所以模式形状函数为零阶贝塞耳函数和诺尔曼函数的线性叠加，即解可设为

ψ=aJ0(ξ)+bN0(ξ)

(20)

将边界条件代人上式有

(21)

方程组(21)有非零解，则必有：

J0(ξ0)N0(ξ1)-J0(ξ1)N0(ξ0)=0

(22)

利用式(16)和(17)，方程(22)可改写成

J0(ε)N0(kε)-J0(kε)N0(ε)=0

(23)

式(23)是关于ε的方程，为考虑重力对张力影响时竖直布置轴向运动弦线的特征方程，其特征根与k有关(即和β有关)，有如下的贝塞耳函数和诺尔曼函数的渐近公式表达式[38]

(24)

(25)

将式(223)用式(24)和式(25)展开并简化,可得

(26)

要使J0(x)N0(kx)-J0(kx)N0(x)=0有解，则有：

显然不存在，舍去。

或

同样无解，舍去。

或

sin[(k-1)ε]=0

(27)

(28)

上式即为无量纲动力学方程的特征频率。由边界条件式(2.21)得

anJ0(εn)+bnN0(εn)=0

(29)

则式(20)的解可化为

(30)

将式(15)代入上式，得到式(14)的解

(31)

上式即为无量纲动力学方程的特征函数(振型函数)。则由振型叠加法可得动力学方程的完整解

(32)

(四)带钢抖动的动力学行为讨论

1.特征频率讨论

当β=0时，即没有重力的作用，方程(12)则改成了两端简支弦的方程

(33)

其特征频率为

ω0n=nπ

(34)

利用上式，式(28)可写为

(35)

从上式即可看出有重力作用弦与无重力作用弦特征频率之间的关系：有重力作用弦的特征频率大小是一个与β有关的系数和无重力作用弦特征频率的乘积。由于无重力作用弦的固有频率为

(36)

(37)

由此可以求得不同工况和带钢规格时，带钢的固有频率(见表1)。

表1 不同带钢规格和工况下的频率分析表

实际生产中，带钢无法改变，只有通过调节张力来控制抖动频率。同一带钢对于不同的张力T，有重力相对无重力弦的固有频率相对误差Er对应不同的值为

(38)

以1.15×1550mm带钢为例，由式(38)可得Er对应张力T的曲线如图4所示。可以看出，重力对带钢固有频率的影响比较小，但也不能完全忽略。张力越大，重力对带钢固有频率的影响越小。

图4 Er随张力变化曲线

2.振型讨论

对式(31)进行化简可得下面形式

(39)

其中：

sinα=

从式(39)可以看出振型有正弦项；正弦项前的式子决定了振幅。同样以如下板型和工况为分析对象做振型分析：

(40)

使用MATLAB求解式(39)，可得该规格带钢的各阶振型，前六阶振型如图5所示。可以看出，振型与一般弦振动类似。一阶振型有一个波峰(波谷)点，二阶振型有两个一个波峰(波谷)点，依次类推n阶振型有n个波峰(波谷)点。

图5 带钢的前六阶振型

由于气刀安装在锌锅上方不远处(到沉没辊轴心的归一化距离为0.0038)，因此从振型可以看出影响气刀工作的是最下面一个节点以下的振动。前六阶振型的最下面一个波峰点(波谷点)的位置坐标x如表2所示，其中x*为对应阶的无重力弦最下面一个波峰点(波谷点)的相应值，Er为两者之差。

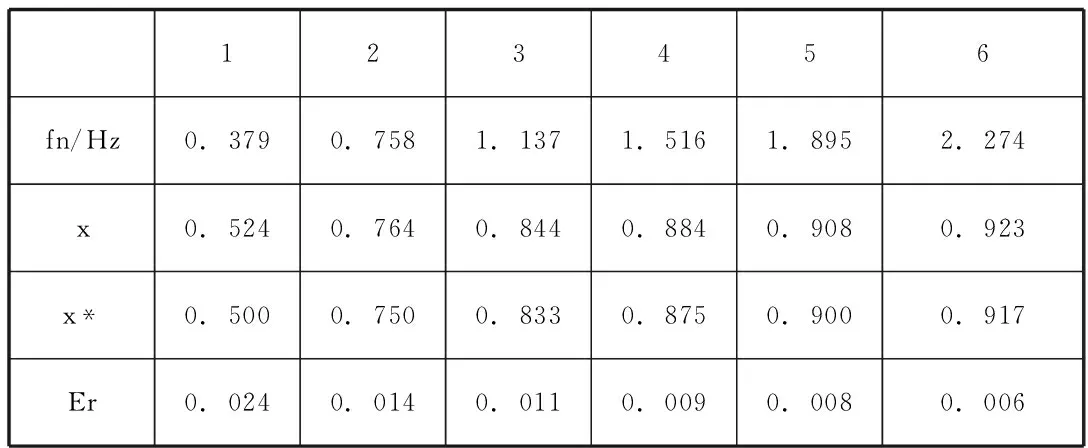
表2 波峰点(波谷点)的自变量坐标位置

从表2可以看出：

1)阶数越高，x越大，即各阶振型的最下面一个波峰点(波谷点)的位置随着阶数的升高而更靠近气刀。说明在同等激励条件下高阶振动比低阶低阶更影响带钢质量。

2)阶数越高，Er越小，说明重力对低阶振型影响较大。但对高阶振型的影响也不可忽视，如：重力影响使第6阶最下面一个波峰点(波谷点)下移了0.006，远大于气刀到沉没辊轴心的归一化距离0.0038。

二、结论

经过定量的分析可以得到以下结论：

1)带钢规格、冷却塔高度和带钢张力决定带钢的特征频率；

2)带钢具有不同的振型，振动频率是基波频率的倍数；

3)带钢的重力对特征频率的影响很小，带钢张力越大，影响因子越小；

4)同等激励时，高阶振动更加影响到带钢在气刀位置的带钢振动幅度。

三、可能采取的治理措施

从上述分析可以知道，要抑制带钢抖动，就需要想办法破坏抖动发生的条件，可以采取的治理措施有：

1)调整带钢运行的速度和张力：改变带钢固有频率，等效于改变了锅内辊对带钢激励扰动的频率，进而改变了张力波动的幅度和频率，达到破坏抖动发生条件；

2)调整纠正辊的啮合量，也可破坏抖动发生条件：调节辊子对带钢的激励扰动；

3)增强塔顶层的刚度：在尽量减小附加荷载和不影响原结构功能发挥的前提下，尽可能提高顶层铅垂向振动的固有频率，调节塔顶转向辊支乘对带钢的激励扰动；

4)对于新改造或设计的机组，可以增加稳定辊和纠正辊的刚度：这对辊子在受力时发生弯曲变形，造成辊轴线方向的平行度变化，从而引起张力沿带钢横截面非均匀分布，使带钢产生单边弓形变形，引起带钢抖动。增加稳定辊和纠正辊的刚度，可以有效降低因这对辊子的变形引起带钢抖动的程度。