基于强度折减法的岩土边坡稳定性影响分析

宋晓立

（凌源市凌河保护区管理局，辽宁 朝阳 122500）

土体流变导致安全事故报道屡见不鲜，边坡失稳严重影响道路安全、社会稳定与行人的生命安全，因此，展开对边坡稳定性的影响研究具有重要的现实意义。国内学者对土体流变行与稳定性进行了大量研究，雷华阳[1]通过研究滨海软土剪切流变的影响因素与结构效应，建立了相对应的流变分析模型。徐平等[2]利用有限元分析软件FLAC3D进行了黏弹性模拟分析，得到义开尔文模型的中心差分格式与基坑开挖中施工变形规律。郭海柱等[3]根据D-P屈服破坏准则与时间硬化幂函数法则耦合流变模型，通过模拟施工过程中深基坑工程变形规律，具有一定的理论意义。

本文从岩土边坡工程角度出发建立了物理模型，选择强度折减法进行混合土边坡稳定性判别，以Mohr-Coulomb屈服准则为破换准则，通过对下边坡流变特性进行分析，考察了弹性模量、黏聚力、泊松比、内摩擦角、坡角等参数对边坡稳定性的影响，为实际工程建设提供了理论指导。

1 模型建立

1.1 物理模型

建立梯型边坡物理模型，如图1，边坡倾斜角度45°，边坡高度13m。

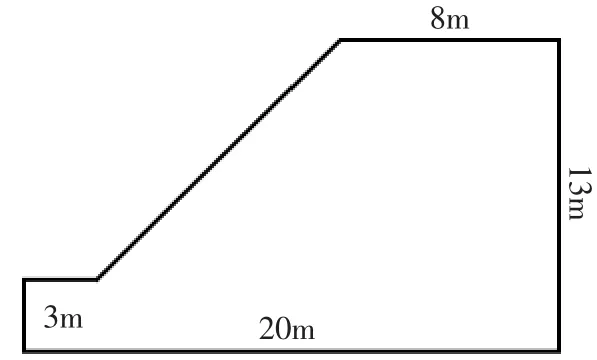
图1 梯型边坡有限元模型

边坡稳定性判别方法有Sarma法、突变理论判别法、条分法等。本次选择强度折减法进行边坡稳定性判别。

该方法利用数值分析得出一个安全系数，称作抗剪强度折减系数。抗剪强度参数可表示为[4-5]：

式中 Fr为强度折减系数；Cm与φm为强度折减后混合土的实际抗剪强度参数；φ为内摩擦角 （°）；c为黏聚力（kPa）。

有限元分析过程中边坡失稳判别依据主要包括4个[6]：

（1）区域内塑性区是否保持贯通。

（2）特征部位发生突变变形，且持续不断发展。

（3）计算所得关键点位移是否发生突变变形。

（4）数值计算结果是否收敛作为判别依据。

屈服准则作为材料是否屈服的判断标准，表示材料在外力作用下由弹性应变转变为塑性应变的过渡点[7]。实际工程中，边坡承受最大剪应力大于边坡本身的抗剪强度，这是引起边坡失稳的主要原因，因此利用强度折减法分析边坡稳定时，需要选取优良的弹塑性模型，以Mohr-Coulomb屈服准则作为破坏准则，具有塑性流动方向唯一、流动趋势光滑和偏应力无死角的优点。Mohr-Coulomb屈服准则公式为：

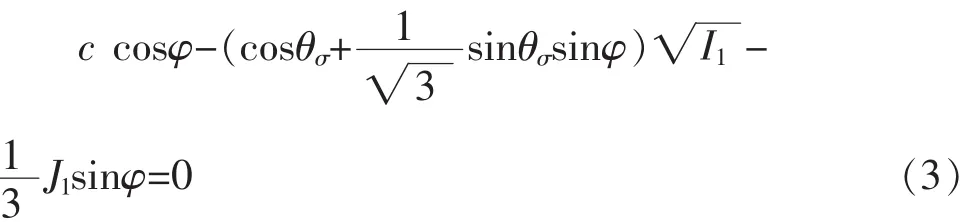
式中 c为黏聚力（kPa）；φ为内摩擦角（°）；θσ为应力罗德角 （°）；I1为应力偏张量的第一不变量；J1为应力张量的第一不变量。

2 边坡稳定性影响因素分析

通过对下边坡流变特性进行分析，考察弹性模量、黏聚力、泊松比、内摩擦角、坡角与剪胀角对边坡稳定性的影响。

2.1 黏聚力影响

根据不同工况计算、分析结果，得到不同黏聚力下的抗剪强度参数，结果如表1与图2。

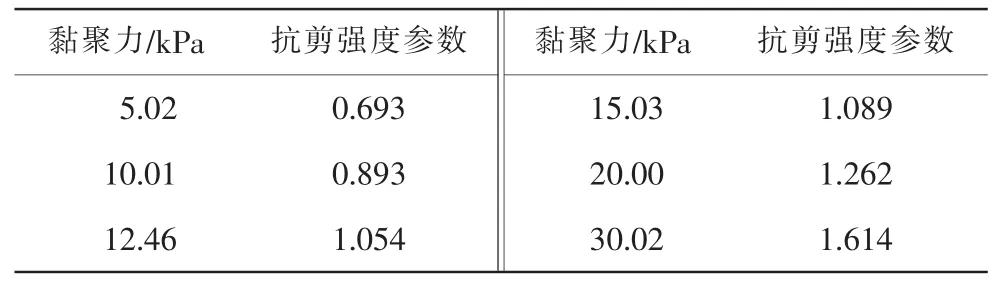
表1 抗剪强度参数与黏聚力关系

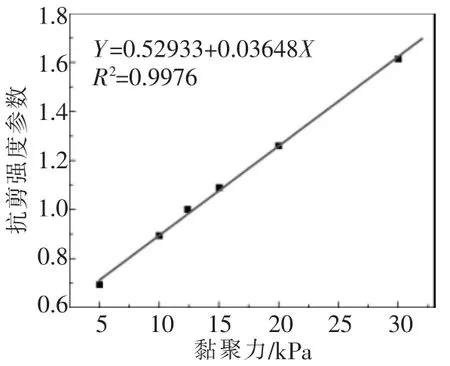
图2 抗剪强度参数与黏聚力关系

由表1与图2发现，边坡抗剪强度参数随着黏聚力的增大呈现不断增大趋势，并且两者呈现线性增长，拟合得到一条线性良好的直线：Y=0.52933+0.03648X。黏聚力不断增大，滑坡体的体积变化由小变大。

2.2 内摩擦角影响

岩土材料的内摩擦角设置区间为[5°，40°]，根据不同工况的计算，得到不同内摩擦角抗剪强度参数，结果如表2与图3。

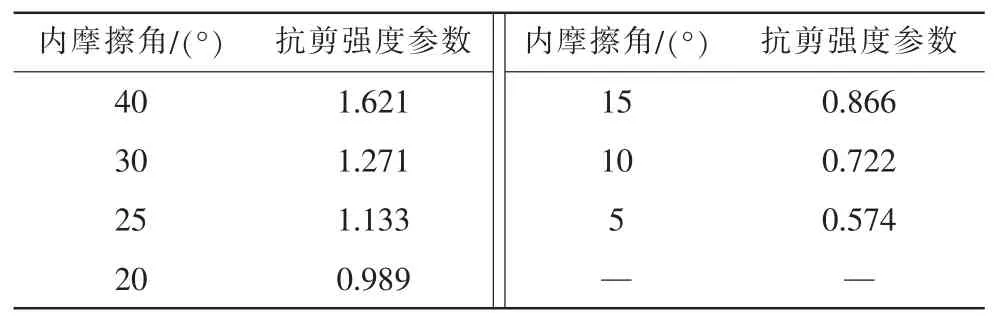
表2 抗剪强度参数与内摩擦角关系

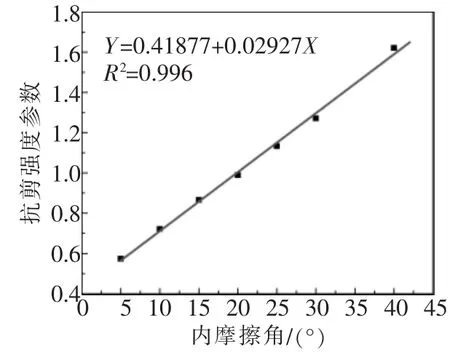
图3 抗剪强度参数与内摩擦角关系

由表2和图3发现，边坡抗剪强度参数随着内摩擦角的增大呈现不断增大趋势，并且通过线性拟合得到一条线性良好的直线：Y=0.41877+0.02927X。滑坡体的体积随着内摩擦角增大不断变小。

2.3 剪胀角影响

岩土材料的剪胀角设置区间为[0°，50°]，根据不同工况的计算、分析结果，得到不同剪胀角下的抗剪强度参数，结果如表3与图4。

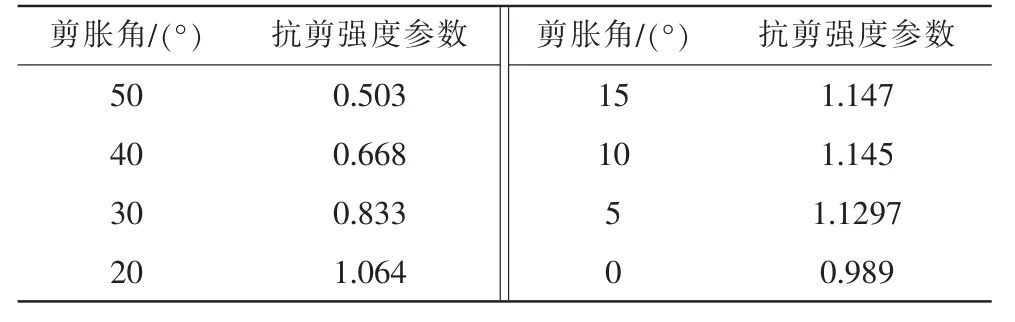
表3 抗剪强度参数与剪胀角的关系

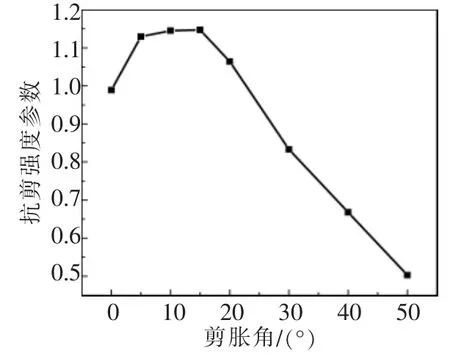
图4 抗剪强度参数与剪胀角关系

由表3和图4发现，边坡抗剪强度参数随着剪胀角增大呈现先增大后减小的趋势，膨胀角小于内摩擦角时，抗剪强度参数变化趋势与内摩擦角相似，随着剪胀角增大而增大，膨胀角大于内摩擦角时，抗剪强度参数明显降低，滑坡体的体积随着膨胀角增大不断变小。

2.4 弹性模量影响

岩土材料的弹性模量变化范围为[50MPa，300MPa]，根据不同工况计算，得到不同弹性模量下的抗剪强度参数，结果如表4。

由表4发现，抗剪强度参数随着弹性模量的增大基本保持不变，滑坡体的体积和滑动面位置随着弹性模量的增大变化很小，因此，实际工程中能够忽略材料弹性模量对边坡稳定性的影响。

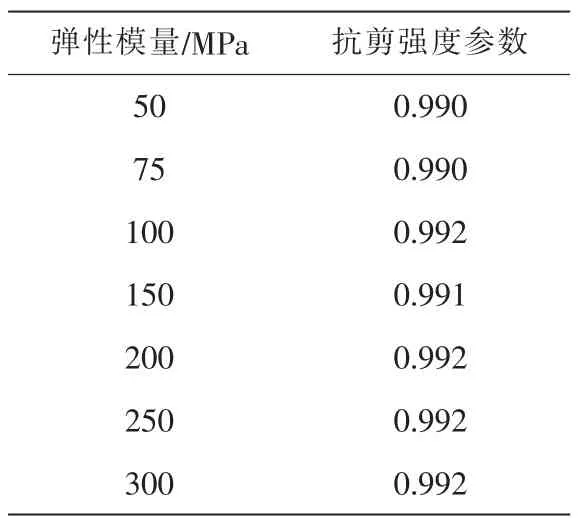
表4 抗剪强度参数与弹性模量关系

2.5 泊松比影响

岩土材料的泊松比变化范围为[0.1，0.4]，根据不同工况的计算、分析结果，得到不同泊松比下的抗剪强度参数，结果如表5。

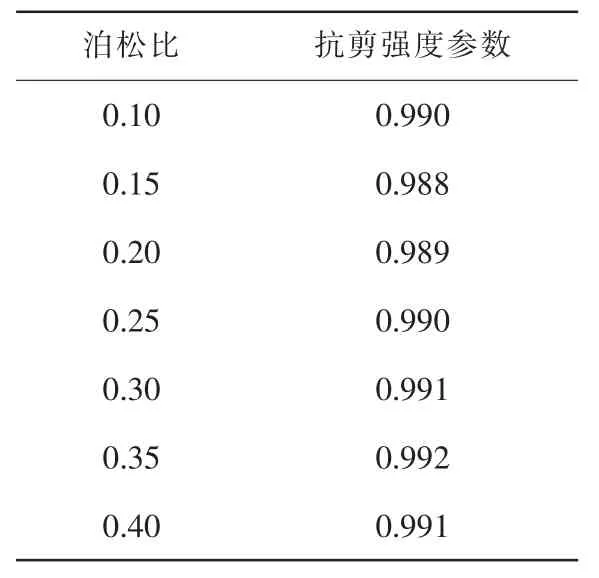
表5 抗剪强度参数与泊松比关系

由表5发现，抗剪强度参数随着泊松比的增大同样保持不变，滑坡体的体积和滑动面位置随着泊松比的增大变化很小，这一点与弹性模量对边坡稳定性的影响相同，因此，实际工程中同样可以忽略材料泊松比对边坡稳定性的影响。

2.6 坡角影响

坡角变化区间为[30°，70°]，根据不同工况计算，得到不同坡角下的抗剪强度参数，结果如表6与图5。

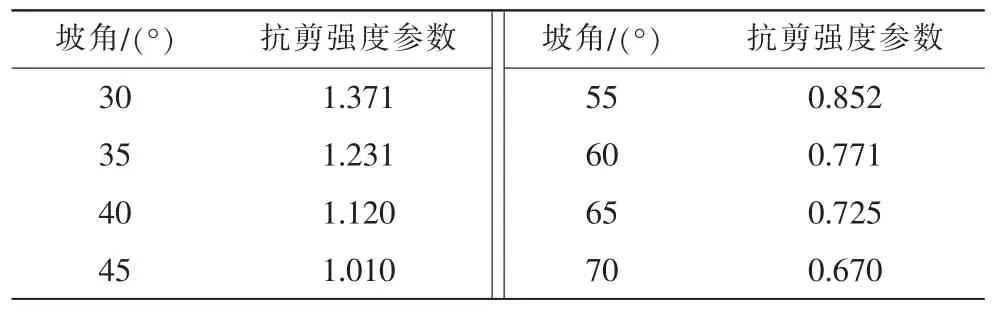
表6 抗剪强度参数与坡角关系

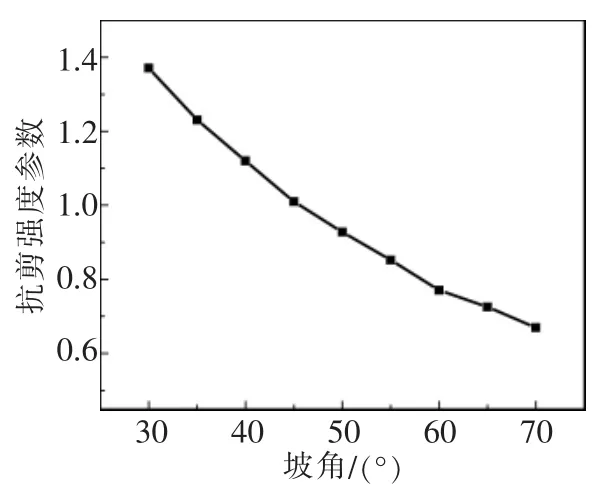
图5 抗剪强度参数与坡角关系

由表6和图5发现，边坡抗剪强度参数随着坡角不断增大呈现不断减小的趋势，滑坡体的体积随着坡角不断增大而变小，滑移面颜色由深变浅，因此，实际工程建设中应该尽可能减小坡角。

3 结语

从岩土边坡工程角度出发建立物理模型，选择强度折减法进行混合土边坡稳定性判别，选择Mohr-Coulomb屈服准则为破换准则，通过对下边坡进行流变特性分析，得出以下结论：

（1）边坡抗剪强度参数随着黏聚力和内摩擦角的增大均呈现不断增大的趋势，滑坡体的体积随着黏聚力不断增大而由小变大，随着内摩擦角增大而逐渐变小，滑移面的变化趋势随着黏聚力和内摩擦角增大均由浅变深。

（2）边坡抗剪强度参数随着剪胀角增大呈现先增大后减小的趋势，滑坡体的体积随着膨胀角增大不断变小，滑移面颜色由深变浅。

（3）抗剪强度参数随着弹性模量和泊松比的增大基本保持不变，滑坡体的体积和滑动面位置随着弹性模量的增大变化也很小。因此，实际工程中可以忽略材料弹性模量和泊松比对边坡稳定性的影响，工程建设中应该尽可能减小坡角。