抗滑桩与边坡夹角对抗滑桩抗滑效果研究
2017-08-30
(重庆交通大学 土木工程学院, 重庆 400074)
抗滑桩与边坡夹角对抗滑桩抗滑效果研究
胡海波
(重庆交通大学 土木工程学院, 重庆 400074)
基于抗滑桩与边坡坡面夹角的大小,采取定性分析和数值模拟的方法对抗滑桩的抗滑效果开展研究,得出了改变抗滑桩与边坡坡面的夹角(以下简称桩坡角)以及边坡坡角均能影响抗滑桩作用效果,当桩坡角约为90°时,抗滑桩对边坡作用效果最佳,此时的抗滑桩在土压力作用下的结果响应最小。
桩坡角;抗滑桩;边坡;抗滑效果
0 引言
在我国,每年因滑坡造成的经济损失数以亿计,滑坡灾害已经与洪水、地震灾害一同被作为全球性三大地质灾害,它们对人类的生命、财产安全造成了严重威胁。我国每年用于滑坡处理施工的抗滑桩超过上万根,单个抗滑桩就达数万元或十万元,可见采用抗滑桩治理滑坡是十分普遍且重要的技术手段,而且工程造价小则几十万,大则上千万。因此,对采用抗滑桩治理滑坡的抗滑效果的研究具有十分重要的意义。[1]
1 Ansys数值模拟分析
1.1 模型概况
选取某滑坡带的边坡,简化后建立有限元模型如图1所示。由于边坡为某一方向无限长的结构体,故采用二维模型进行分析。边坡考虑弹性和弹塑性两种材料,以边坡滑体沿着X轴方向的最大位移作为衡量抗滑桩对边坡作用效果的评价指标。X轴方向的最大位移越小,说明边坡的变形越小,抗滑桩作用效果越好。[3]
输入模型的参数如下,A1区域土体弹性模量为3×106Pa,泊松比为0.24,密度为2700,粘聚力9×105Pa,摩擦角为42°。A2区域土体弹性模量为2.9×106Pa,泊松比为0.25,密度为2500,粘聚力9×105Pa,摩擦角为40°。A3区域抗滑桩弹性模量为4×1010Pa,泊松比为0.3。

图1 ANSYS模型二维平面图
1.2 最佳桩坡角的分析确定
1.2.1 滑体最大位移与桩坡角、坡角的关系
采用ansys建立的边坡有限元模型,计算出滑体在不同桩坡角、边坡坡角时的最大位移值如表1,由表1绘制图2。

表1 滑体最大位移值和坡顶X方向最大位移值
由图2可知,在边坡坡角为40°~80°范围内,随着桩坡角的增大,最大位移值小幅度上升。当坡角较大时,桩坡角对最大位移值的影响较小,可忽略不计。
在桩坡角为67.5°~112.5°的范围内,随着坡角的增大,最大位移值随之增大,而且增长速率减小。由此,根据材料力学和平衡力学原理可分析得出,边坡模型符合实际,可由该模型分析推导其他理论参数。
1.2.2 由坡顶X方向最大位移确定最佳桩坡角
计算出边坡坡顶在不同桩坡角、边坡坡角时的X方向最大位移值如表1,由表1绘制图3。
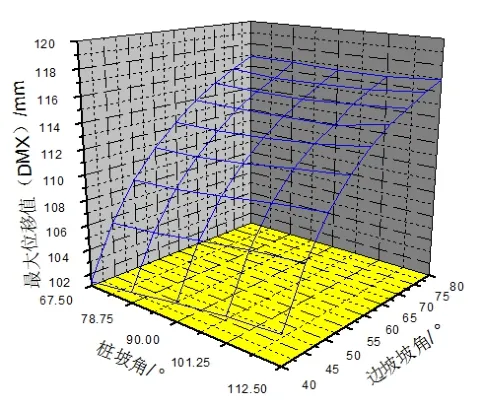
图2 滑体最大位移与桩坡角、坡角的关系图

图3 坡顶X方向最大位移与桩坡角、坡角的关系图
由图3可知,在边坡坡角为40°~80°范围内,桩坡角在67.5°→90°时,X方向的位移减小;桩坡角在90°→112.5°时,X方向的位移增大。桩坡角约为90°时X方向的位移最小。因此90°为桩坡角的最佳值,此时抗滑桩对边坡的抗滑作用最大。故可建议实际工程中,在施工条件满足时,以90°作为桩坡角的设计建议值。
在桩坡角为67.5°~112.5°范围内,边坡坡角在40°→65°时,X方向的位移显著增大;边坡坡角在65°→80°时,X方向的位移显著减小。造成该现象的原因为坡角为40°→65°时,滑体自重逐渐增大,重心对滑动面上半部分(斜率较大,接近垂直)作用明显,使得X方向的位移随着滑体向下移动而增大;边坡坡角在65°→80°时,滑体自重进一步增大,重心对滑动面下半部分(斜率较小,接近水平)作用明显,使得滑体的作用力更多的作用在接近水平的滑动面上,故X方向的位移减小。
2 结论
(1)桩坡角是影响抗滑桩对边坡作用效果的重要因素;
(2)当桩坡角约为90°时,此时抗滑桩对边坡作用效果最佳。在施工条件满足要求时,可采用桩坡角为90°来设计抗滑桩;
(3)不同边坡坡角下,最佳桩坡角均约为90°。边坡坡角对最佳桩坡角影响不明显。
[1]年廷凯,徐海洋,刘红帅.抗滑桩加固边坡三维数值分析中的几个问题[J].岩土力学,2012,33(8):2521-2526.
[2]戴自航,徐祥.边坡抗滑桩设计计算的三维有限元法[J].岩石力学与工程学报,2012,31(12):2572-2578.
[3]张爱军.挡土桩—土相互作用模型及抗滑桩加固边坡简化计算方法研究[D].华南理工大学,2013.
G322
:B
1007-6344(2017)08-0323-01
胡海波(1992-),男,重庆人,硕士在读研究生,研究方向为城市道路和交通工程设计理论与养护技术。
