Stability analysis of lead-vehicle control model in cooperative adaptive cruise control platoon within heterogeneous traffic flow

Gu Haiyan Zhang Jian Jin Peter J. Ran Bin

(1School of Transportation, Southeast University, Nanjing 210096, China)(2College of Transportation Science & Engineering, Nanjing Tech University, Nanjing 210009, China)(3Department of Civil and Environmental Engineering, The State University of New Jersey, Piscataway, NJ 08854, USA)

Abstract：In order to analyze the stability impact of cooperative adaptive cruise control (CACC) platoon, an adaptive control model designed for the lead vehicle in a CACC platoon (LCACC model) in heterogeneous traffic flow with both CACC and manual vehicles is proposed. Considering the communication delay of a CACC platoon, a frequency-domain approach is taken to analyze the stability conditions of the novel lead-vehicle CACC model. Field trajectory data from the next-generation simulation (NGSIM) data is used as the initial condition. To account for car-following behaviors in reality, an intelligent driver model (IDM) is calibrated with the same NGSIM dataset from a previous study to model manual vehicles. The stability conditions of the proposed model are validated by the ring-road stability analysis. The ring-road test results indicate the potential of the LCACC model for improving the traffic flow stability impact of CACC platoons. Sensitivity analysis shows that the CACC fleet size has impact on the parameters of the LCACC model.

Keywords：stability analysis; cooperative adaptive cruise control (CACC) platoon; lead-vehicle model; frequency-domain approach

Freeway traffic flow control requires mathematical models to describe the characteristics of traffic flow. These models must capture the essential character of the traffic flow behavior to develop the effective state estimation, filtering and control algorithms. Various categories of traffic flow models have been developed by researchers in the past to support simulation and control design[1-2]. The car following models[3]focus on the microscopic characteristics of traffic flow, such as lane-changing behavior, car-following behavior, and traffic trajectory.

Adaptive cruise control (ACC) systems, one type of driving-assistant system, aim to comfort drivers by releasing driving tasks and to benefit traffic efficiency and safety, have been developed for more than ten years and are even used on the market in some countries. The existing research work, based on microscopic simulations, has also proven that ACC systems can contribute to the stabilization, fuel economy and exhaust emissions of the corresponding traffic flow[4-7].With the emergence of reliable vehicle-to-vehicle (V2V) communications, the next step in the development of ACC points is to cooperate with V2V communications to obtain more extensive and reliable information on vehicles.

The cooperative adaptive cruise control (CACC) system, which is an extension of the ACC system concept, is a new realization of longitudinal automated vehicle control. Compared with the ACC system, the CACC system can provide much more information about the surrounding vehicles through the vehicle-to-vehicle wireless communication mechanism. The impacts of CACC systems on traffic flow characteristics have recently been widely evaluated through microsimulation and experimental studies[8-11].

The focus of this study, however, is on the stability of heterogeneous traffic flow that contains CACC platoons and manual driving vehicles, based on the evaluation framework proposed in Ref.[12]. All the vehicles in the traffic flow can be sorted into two types, which are manual driving vehicles and CACC platoons. A novel lead-vehicle CACC (LCACC) model is used to simulate the car-following behavior of the lead vehicle of CACC platoon. A normal CACC model is used to describe CACC vehicles characteristics. Manual driving vehicles are modeled by the IDM.

1 Related Work

Two different criteria for stability that are central to the study of traffic flow problems should be considered: string stability and traffic flow stability. Some researchers have physically motivated and then mathematically defined the string stability and traffic flow stability and the difference between the two[13]. With the development of ACC/CACC, there are some impacts on the methods of stability analysis.

1.1 Simulation method

A traffic simulation model MIXIC was developed in Ref.[14] to describe the impact of CACC on traffic performance, traffic safety, exhaust-gas emission, and noise emission. The results show an improvement in traffic stability and a slight increase in traffic-flow efficiency compared with that of the merging scenario without equipped vehicles[8]. The Newell model was used in simulation to analyze the influence of V2V on traffic flow string stability[15].

1.2 Analytical method

1.2.1 A frequency-domain approach for string stability

For a constant velocity-independent intervehicle spacing, string stability cannot be guaranteed. The theoretical finding can be further validated by experiments conducted with two CACC-equipped vehicles. The string-stability characteristics of the CACC system are analyzed using a frequency-domain-based approach[16].

In Fig.1,Gi=Gi(s) represents the dynamics of thei-th vehicle;Ki=Ki(s) is the corresponding ACC feedback controller;Fi=Fi(s) is the feedforward filter;Di=Di(s) is the communication delay;sis the Laplace operator; andhd,iis the headway time. For clarity, the time dependency of the signals is omitted. The experimental results yield significant findings for CACC. With the relatively simple vehicular system and standard ACC algorithm, there have been significant improvements on the minimal headway time and string-stability characteristics[17]. Guo et al.[18]presented a systematic method that can guarantee string stability, achieve zero steady-state spacing error, and ensure a certain level of control performance at the same time.

Fig.1 CACC control diagram

1.2.2 Space error method for string stability

The string stability is defined as spacing errors, i.e., in a string-stable platoon, the spacing errors between vehicles are not amplified when propagating toward the tail of the platoon.Eiis denoted as the spacing error between two adjacent vehicles. Then, the string stability implies that

(1)

whereE(s) is the Laplace transform of the spacing error. This definition is adopted by many researchers[19-20]. However, in the grand cooperative driving challenge (GCDC), string stability is defined using the vehicle accelerations[21]:

(2)

whereA(s) is the Laplace transform of the vehicle acceleration. Such a criterion is used to guarantee that the accelerations are not amplified upstream in the platoon.

1.2.3 String stability for heterogeneous traffic

A longitudinal controller that uses the information exchanged via wireless communication with other cooperative vehicles to achieve string-stable platoon is developed[9]. An appropriate sensitivity function for heterogeneous traffic shown in Ref.[22] is

(3)

wheremis the number of vehicles in the platoon andXiis the Laplace transforms of the location of vehiclei. IfXiis the leading vehicle, thenXi=SiSi-1…S2S1, and a necessary condition to avoid amplification of oscillation is that

‖Si‖∀i

Considering the switch to ACC, we obtain

(4)

1.2.4 Linear stability for heterogeneous traffic flow

Ngoduy[23]conducted a linear stability analysis to find the stability threshold of heterogeneous traffic flow using car-following models. The effect of intelligent vehicles on heterogeneous (or multiclass) traffic flow instabilities is analyzed. The results show how intelligent vehicle percentages affect the stability of multiclass traffic flow. This paper extends to the multiclass time-continuous intelligent driver model with time delays[24]. Most current analytical research has only relied on single-class traffic flow dynamics.

2 Methodology

As discussed in Ref.[12], we consider a platoon ofn+mvehicles traveling in a single lane as shown in Fig.2. The precedingmvehicles are not equipped with CACC vehicles and are assumed to be human-driven. The leading vehicle implements acceleration using acceleration signals received from preceding vehicles through radar. We assume that the leading vehicle can only sense the velocity and distance information from one preceding vehicle assuming no communication between leading vehicles and manually driven vehicles. CACC vehicles share the prevailing states of vehicles among CACC platoons such as distance, velocity and acceleration.

Fig.2 A mixed manual and CACC vehicle platoon

2.1 LCACC and CACC model equation

Microscopic traffic flow models describe the motion of individual vehiclenin response to its leading vehiclen-1. In this paper, we use the LCACC model[12]for the leading vehicle of the CACC platoon:

(5)

whereNis the number of CACC vehicles;vp(t) is the velocity of the manual driving vehicle in front of the leading vehicle;k0,k1,k2are the positive parameters; andα,βare the contribution percentages of forward and backward;ci,des(t) is the designed clearance between vehicleiand the preceding vehicle;ci(t) is the actual clearance between vehicleiand the preceding vehicle.

For the rest of the vehicles in CACC platoon, the following CACC model is used[25]:

an(t)=k0a0(t)+k1(vn-1(t)-vn(t))+

k2(cn(t)-cn,des(t))d2≤an(t)≤amax

(6)

whereamaxis the maximum allowed acceleration andd2is the braking capability of following vehicles. The vehicle spacingvn(t) is the velocity of vehiclenat timet.

(7)

wherecd,csafe,c0.5sare desired, safety, andt-second-time-gap spacing, respectively;δis the communication delay;d1is the braking capability of the preceding vehicle; andd2is the braking capability of the following vehicle.

The intelligent driver model (IDM)[26]is also introduced to control the ACC/CACC vehicles. The IDM acceleration is given by

(8)

wheres0is the minimum distance in congested traffic flow;Tis a constant safe time gap;v0is the desired speed on a free road;vis the actual speed on a free road;ais the maximum acceleration; andbis the comfortable deceleration;sis the spacing between vehicle (n-1) and vehiclenat timet;Δvis the velocity difference between vehicle (n-1) and vehiclenat timet; andαis a constant.

2.2 CACC control structure

Fig.3 Schematic of a platoon of CACC vehicles

ei(t)=xr,i(t)-xr,d,i(t)

(9)

The relationship between time headway and desired distance is

(10)

The acceleration of the preceding vehicle is used as a feedforward control signal through a feedforward filterFi(s). The acceleration is obtained through wireless communication, which includes a communication delayDi(s). The resulting control structure is schematically depicted in Fig.4. In this paper, the focus is not on a single CACC vehicle but on a CACC platoon. The control structure is shown in Fig.5.

Fig.4 CACC control structure[16]

Fig.5 CACC platoon control structure

2.3 String stability

The delay is represented by a constant delay timeθi, yielding

(11)

whereDi(s)=e-θis,fori>1, andL( ·) denotes the Laplace transformation. The design of the feedforward filter is based on a zero-error condition, where the Laplace transform of the errorei(t) is defined as

(12)

Consider the CACC control structure[16]shown in Fig. 4. Coupling some of these control structures yields the control structure for a platoon of vehicles, as shown in Fig.5, where the inner and the outer control loops are merged using the definition ofHi(s).

Hi(s)=1+hd,isi>1

(13)

The first vehicle in the platoon (i=1) is assumed to follow a given time-varying reference positionx0(t) using radar measurements. The other vehicles in the platoon (i>1) use both radar and wireless communication.

The Laplace transforms of input are defined asL(x0(t))=X0(s), and the signals are defined asvi(t),xi(t),ei(t).L(vi(t))=Vi(s),L(xi(t))=Xi(s), andL(ei(t))=Ei(s). We define the following string stability transfer functions:

(14)

(15)

where ‖g‖denotes the maximum amplitude for allω.

(16)

For heterogeneous traffic, i.e., vehicles with potentially different characteristics and dynamics, this condition requires a complicated communication mechanism. In this paper, for the communication in the platoon, since only the leading vehicle is considered, all the vehicles in CACC platoon should satisfy the string-stability transfer functions in (14). In the rest of this paper, the sufficient condition (16) is considered a necessary condition for string stability.

(17)

(18)

(19)

where Ξi(s)=Hi(s)Gi(s)Fi(s)Di(s)s2,Si(s)=(1+Hi(s)Gi(s)Ki(s))-1.

Substituting the feedforward filterFi(s) in (18) yields

Fi(s)=(Hi(s)Gi(s)s2)-1i>1

(20)

(21)

Case1No communication delay. According to the assumption, there is no communication delay between the following vehicles in the CACC platoon,θi=0 s,Di=1, Eq.(21) can be simplified as

(22)

For any time headwayhd,is>0,

(23)

Hence, for the time headwayhd,i>0 s, the string stability condition (18) is always fulfilled.

Case2Communication delayθi>0 s. Theθivalues ranged from 0.3 to 0.6 s is used between the leading vehicle and the following vehicles based on prior research. The external feedforward of the lead vehicle in a CACC platoon is ignored. First, by considering the engine time constant, we have the dynamics of then-th vehicle as

(24)

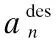
(25)

(26)

By differentiating both sides of Eq.(26), we obtain

(27)

By taking the Laplace transformation on both sides of (27), we can obtain the relationship between vehiclenandn-1 as

(28)

To achieve the string stability, spacing error must be smaller than or equal to the spacing error input. For a CACC vehicle platoon, the string stability is defined as

(29)

According to the assumptions, the delay only exists between the leading vehicle and the following vehicle. All the following vehicles will make a decision at the same time. In this way, we only consider the situation whenn=2.

(30)

Eq.(30) can be simplified as

(31)

where

‖Vn(s)/Vn-1(s)‖≤1 can be satisfied whenp0.

(32)

In the selected CACC model, all parametersk0,k1,k2are greater than or equal to zero. Four different situations are considered based on the values ofk0,k1,k2. Tab.1 summarizes the value range ofτnwith different values of parametersk0,k1,k2ensuring stability, whereτn∈(τ-,τ+).

Tab.1 Stability condition with different values of parameters in the LCACC model

3 Experimental Results and Analysis

3.1 Initial input data design

The ring road is closed by making the back bumper location of the first and the 35th vehicle the same point in the initial state. The inner lane data is used to obtain a real-world “pipeline” scenario close to the ring-road environment. Secondly, the IDM model parameters calibrated based on the same dataset in a previous study are used for modeling manual vehicles. The CACC and LCACC models are applied continuously for 1 000 time intervals to evaluate their stability patterns. The initial speeds of all vehicles are approximately the same (32.9 km/h), and the clearance between any two vehicles is the same. Additionally, the acceleration is zero for all the vehicles. At the timet=0 s, a small disturbance will be added to one vehicle in the stable traffic flow.

3.2 Ring-road test of string stability

Two experiments are performed with different model parameter settings:

1) A CACC platoon using LCACC. We use the LCACC model to simulate the characteristic of lead vehicle of the CACC platoon, the normal CACC model for the rest of the CACC vehicle platoon, and the IDM model for manual vehicles.

2) A CACC vehicle platoon without using LCACC (CACC). All the CACC vehicles are simulated by a normal CACC model, and the manual vehicles are modeled with IDM.

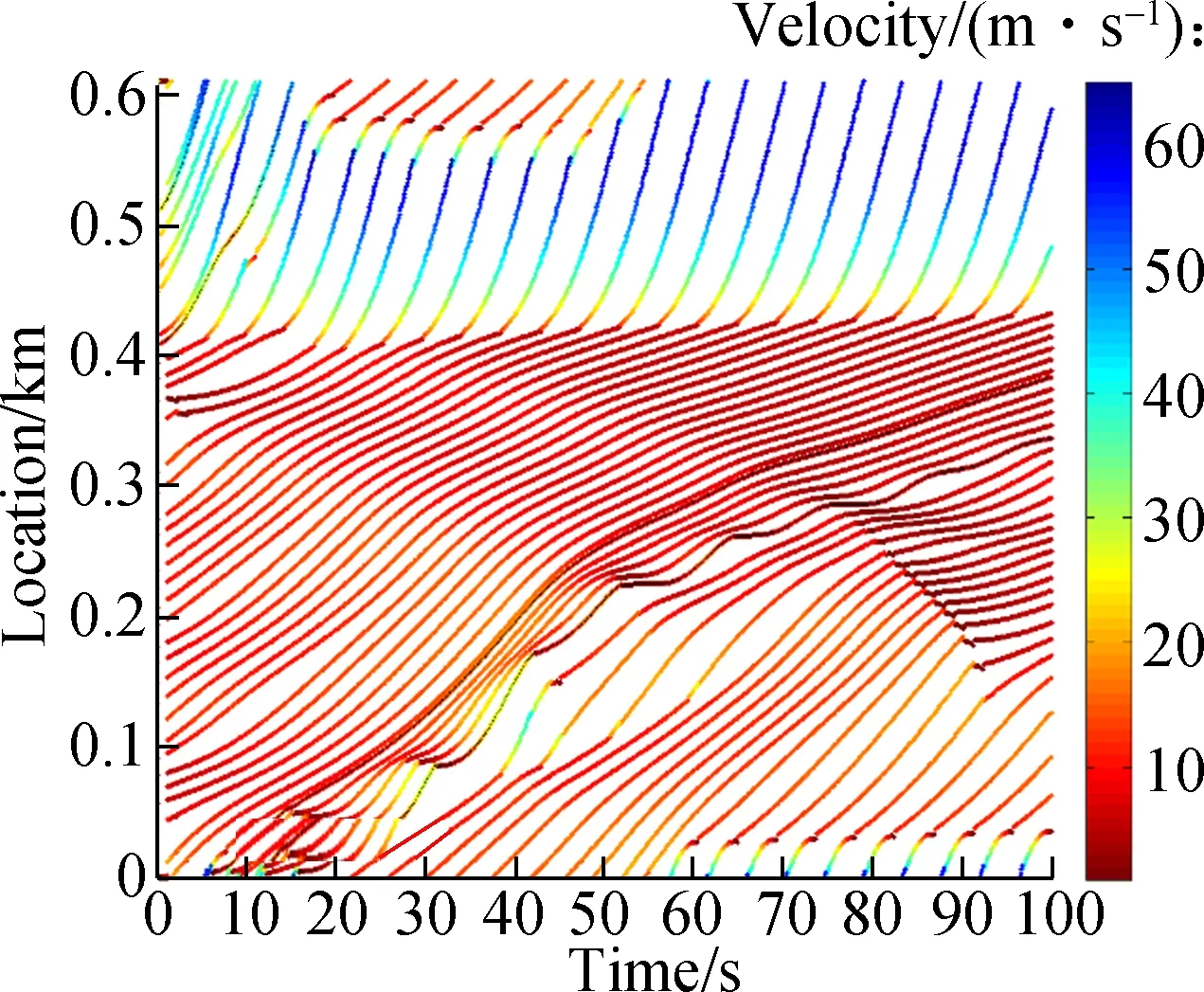
Fig.6 and Fig.7 exhibit the stability characteristics of different evaluation scenarios. TheX-axis represents the simulation time step (0 to 1 000 time steps), they-axis represents the ring-road length (0 to 0.6 km). Color coding displays the velocity (0 to 65 km/h, 18.06 m/s), and 5, 10, 20 are the CACC fleet size. The individual points in each diagram are the trajectory points of vehicles traveling in the ring-road. The color of each point is determined based on the velocity, with blue indicating the free flow and red indicating slow-moving or stopping points. Fig.6 and Fig.7 confirm the numerical results, indicating string stability both in the case of CACC and LCACC with a desired headway time. With the increase in the CACC fleet size, the string stability condition is not always satisfied. For a fixed time headway, the LCACC model is more stable than the CACC model. When the time headway is smaller than 0.5 s, the string stability condition is not satisfied for both LCACC and CACC scenarios.

(a)(b)(c)

(d)(e)(f)

Fig.6Ring-road stability test results for designed time headwayhd,i=0.5 s. (a) LCACC-5; (b) CACC-5;(c) LACCC-10; (d) CACC-10; (e) LCACC-20; (f) CACC-20

(a)(b)(c)

(d)(e)(f)

Fig.7Ring-road stability test results for designed time headwayhd,i=1.5 s. (a) LCACC-5; (b) CACC-5;(c) LACCC-10; (d) CACC-10; (e) LCACC-20; (f) CACC-20

3.3 Stability experiment with NGSIM data

This study used vehicle trajectory data collected in a southbound direction of US Highway 101 (Hollywood Freeway) in Los Angeles, California on June 15th, 2005, from the NGSIM project. The data collection time period is 45 min, between 07:50 and 08:35, during the morning peak hours with a temporal resolution of 0.1 s. First, the states of the last 35 vehicles on Lane 1 at 08:30 during peak hour congestion are used as the initial traffic states on the ring-road. This information establishes a realistic “perturbation pattern” of heterogeneous acceleration, velocity, and spacing for stability analysis. The ring road is closed by making the back bumper location of the first and the 35th vehicle the same point at the initial state.

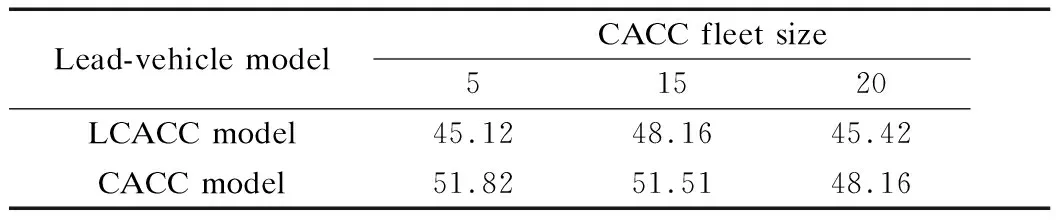
Tab.2 depicts the comparison results for LCACC, CACC, and manual driving under different CACC fleet sizes. The first noticeable pattern is that car-following models, although calibrated from the same NGSIM dataset and started from the same initial condition, can exhibit significantly different stability results. The size of the congestion area (CA) is also shown in the table and used as a car-following stability indicator where larger values mean higher congestion (instability). CA is obtained by the total size of all the vehicles in 10 s by a 30.4 m range, which has an average vehicle velocity below 30 km/h. The stability can also be evaluated by inspecting the frequency of congestion bands.

Tab.2 Congestion area for mixed traffic flow condition

In general, the string stability of vehicles with CACC and LCACC platoons is better than that of all manual vehicles, with significantly reduced CA values shown in Tab.2. With the increase in the CACC fleet size, the trend of the CA value decreases. The heavy low-frequency congestion is reduced to light congestion with increased frequency. Meanwhile, LCACC platoons also exhibit a better capability of stabilizing traffic flow than regular CACC platoons. Furthermore, the increase in the CACC fleet sizes, in general, results in the increased traffic stability.

4 Conclusions

1) If there is no communication delay, the CACC platoon will always satisfy the string stability condition. If a communication delay exists, the stability conditions are related to different values of parametersk0,k, andk2.

2) With the sensing and communication delay, more similar to real-life CACC platoons, the LCACC model can enable small vehicle spacing while maintaining string stability better than that of the CACC model.

3) For the LCACC model, the increase in the CACC fleet size will lead to better string stability.

4) The experimental results show a significant improvement on the minimal headway time using the LCACC model.