Analogy-based software effort estimation using multi-objective feature selection

Chen Xiang Lu Fengyan Shen Yuxiang Xie Junfeng Wen Wanzhi

(1School of Computer Science and Technology, Nantong University, Nantong 226019, China)(2State Key Laboratory for Novel Software Technology, Nanjing University, Nanjing 210023, China)

Abstract：The feature selection in analogy-based software effort estimation (ASEE) is formulized as a multi-objective optimization problem. One objective is designed to maximize the effort estimation accuracy and the other objective is designed to minimize the number of selected features. Based on these two potential conflict objectives, a novel wrapper-based feature selection method, multi-objective feature selection for analogy-based software effort estimation (MASE), is proposed. In the empirical studies, 77 projects in Desharnais and 62 projects in Maxwell from the real world are selected as the evaluation objects and the proposed method MASE is compared with some baseline methods. Final results show that the proposed method can achieve better performance by selecting fewer features when considering MMRE (mean magnitude of relative error), MdMRE (median magnitude of relative error), PRED (0.25), and SA(standardized accuracy) performance metrics.

Keywords：software effort estimation; multi-objective optimization; case-based reasoning; feature selection; empirical study

Software effort estimation (SEE) is one of crucial activities in software project management. If the estimation of the software effort is not accurate, it will be difficult to plan, monitor and control the project stringently. Dejaeger et al.[1]proposed different methods for SEE, such as expert judgment, parameter models, and machine learning methods. Machine learning methods are mostly adopted SEE methods in both industry and research communities. These methods include analogy-based methods, regression-based methods (such as classification and regression trees, ordinary least squares), and search-based methods (such as genetic programming, Tabu search). This paper mainly focuses on analogy-based software effort estimation (ASEE)[2-4].

ASEE is mainly motivated by case-based reasoning[5]. The fundamental assumption of ASEE is that when given a new project to estimate its effort, the most similar historical projects are selected to predict the effort of this new project by using a specific similarity function. It was first proposed by Shepperd and Schofield[6]and then the ANGEL tool was developed by them to incorporate this method. In particular, they used the Euclidean distance to find the projects similar to the target project and used a brute force algorithm to find the optimal feature subset.

The similarity function is one of the most important components in ASEE; therefore, the choice of project features has a large impact on the similarity measure. Feature selection aims to find the optimal feature subset that can achieve better performance. Nowadays, researchers have tried to apply feature selection to ASEE[6-8]. However, none of them modeled this problem as a multi-objective optimization problem. To the best of our knowledge, we first apply feature selection to ASEE using multi-objective optimization. In particular, we mainly consider two objectives. One objective is designed to minimize the number of selected features. The other objective is designed to maximize the performance of ASEE. Based on these two optimization objectives, we proposed the MASE method, which is mainly based on NSGA-Ⅱ[9]. To verify the effectiveness of our proposed method, we design and conduct a series of empirical studies. We choose Desharnais and Maxwell datasets, which include 139 projects from real world. We use MMRE, MdMRE, and PRED(0.25) metrics to evaluate the performance of ASEE. The proposed method is compared with some classical baseline methods (such as NOFS, BSFS, FSFS, SOFS). In particular, no feature selection (NOFS) does not consider feature selection. Backward-selection-based feature selection (BSFS) and forward-selection-based feature selection (FSFS)[7]denote wrapper-based feature selection methods using greedy backward selection and greedy forward selection strategies. Single objective-based feature selection (SOFS) denotes a wrapper based feature selection method using single objective optimization. We find that the proposed method MASE can select fewer features and achieve better performance. Also, the computational cost of MASE is acceptable.

In this paper, a novel wrapper-based feature selection method MASE using multi-objective optimization for ASEE is proposed. Empirical studies are designed and performed using 139 projects from the real world to verify the effectiveness of the proposed method.

1 Background and Related Work

1.1 Analogy-based software effort estimation

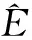
The similarity function measures the level of similarity between projects. Most researchers use the Euclidean distance or Manhattan distance as the similarity function. The number of analogiesKrefers to the number of the most similar projects that will be used to generate the estimation of the target project.K={1,2,3,4,5} can cover most of the suggested numbers. After the analogies are selected, the estimated effort for the target project is determined by the adaptation techniques[10], such as the closest analogy, the mean (or median) of the analogies, or the inverse distance weighted mean.

1.2 Feature selection for software effort estimation

Data preprocessing is a fundamental stage of the ASEE, such as feature selection, case selection, missing-data treatments[11-12]. Feature selection aims to identify and remove as many as possible irrelevant and redundant features. Here, an irrelevant feature is a feature which has little correlation with the estimated effort. A redundant feature is a feature which contains information from one or more other features. The existing feature selection methods can be classified into filter-based and wrapper-based methods. The wrapper-based methods evaluate the goodness of a feature subset using the performance of the model, and the filter-based methods use general characteristics of datasets to evaluate the quality of the feature subset.

In previous studies, researchers attempted to apply feature selection to improve the performance of ASEE. Shepperd and Schofield[6]employed an exhaustive search to find the optimal feature subset. Kirsopp et al.[7]considered hill climbing and forward sequential selection strategies. Later, Li et al.[8]proposed a hybrid feature selection method. In particular, they obtained the feature subsets to maximize mutual information in the internal stage and they searched for the best number of feature subsets in the external stage by minimizing the performance of ASEE on the training set. Moreover, feature selection is also used for other machine learning-based software effort estimation methods[13-14].

Different from previous studies, we formalize the feature selection in ASEE as a multi-objective optimization problem and then propose an MASE method.

2 The Proposed Method MASE

Our research is motivated by the idea of search-based software engineering (SBSE)[15]. The concept of SBSE was first proposed by Harman et al[15]. It has become a hot research topic in recent software engineering research. SBSE has been applied to many problems throughout the software life cycle, from requirement analysis and software design to software maintenance. The approach is promising since it can provide automated or semi-automated solutions in situations with large complex problem spaces, which have multiple competing or even conflicting objectives.

When applying feature selection to ASEE, we consider two objectives. One objective is considered from the benefit aspect and it aims to maximize estimation accuracy. The other objective is considered from the cost aspect and it aims to minimize the number of selected features.

To facilitate the subsequent description of our proposed MASE method, we first give some definitions concerning about the multi-objective optimization algorithm.

Definition1(Pareto dominance) Supposing that FSiand FSjare two feasible solutions, we call FSithe Pareto dominance on FSj, if and only if:

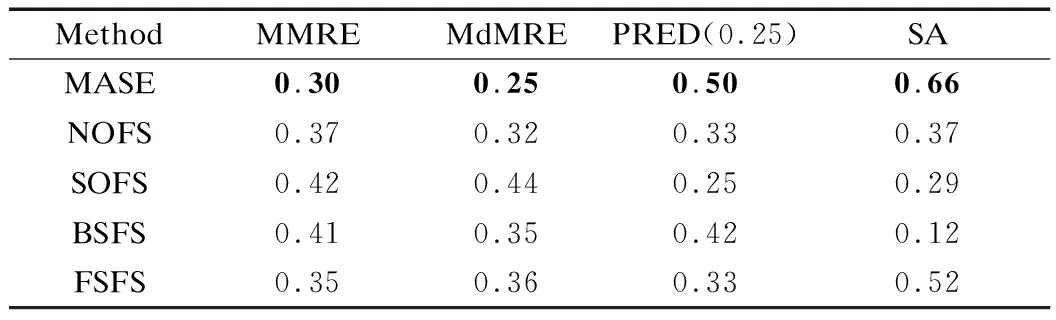
benefit(FSi)

or

benefit(FSi)≤benefit(FSj) and cost(FSi)

where FSiand FSjdenote the selected feature subsets. Function benefit() returns the estimation accuracy of ASEE when using the given feature subset. Here, we use MMRE performance metric, which will be introduced in Section 3. The smaller the value, the better the performance. Function cost() returns the number of selected features.

Definition2(Pareto optimal solution) A feasible solution FS is a Pareto optimal solution, if and only if there is no other feasible solution FS*which is the Pareto dominance on FS.

Definition3(Pareto optimal set) This set is composed of all the Pareto optimal solutions.

Definition4(Pareto front) The surface composed of the vectors corresponding to all the Pareto optimal solutions is called the Pareto front.

Researchers have proposed many different multi-objective algorithms (MOAs). These algorithms use evolutionary algorithms to construct the Pareto optimal set. Our proposed MASE is mainly designed based on NSGA-Ⅱ[9], which is a classical MOA.

Before introducing our method MASE in detail, we first show the coding schema of the chromosome. We can encode a feasible solution intonbit string if a dataset hasnfeatures. If the value of thei-th bit is 1, it means that thei-th feature is selected. Otherwise, if the value is 0, it means that thei-th feature is not selected. To compute the benefit of the solution, we can utilize ASEE to compute the MMRE on the training set based on the selected features.

NSGA-Ⅱ first initializes population. The population hasNchromosomes and each chromosome is randomly generated. Then, it uses classical evolutionary operators to generate new chromosomes. In particular, the crossover operator will randomly choose two chromosomes according to crossover probability, perform crossover operation, and generate two new chromosomes. The mutation operator will randomly choose a chromosome according to mutation probability, perform the mutation operation, and generate one new chromosome. Later, it performs a selection operation to select high-quality chromosomes based on the Pareto dominance analysis and put these chromosomes into the new population. This process is optimized by using the fast non-dominated sorting algorithm and the concept of crowding distance. After a sufficient population evolution, it will satisfy the termination criterion and converge to stable solutions. Finally, it returns all the Pareto optimal solutions in the current population.

Here, all the Pareto optimal solutions are constructed based on the training set, and we use these selected feature subsets to compute MMRE by using ASEE on the testing set.

3 Experimental Setup

To verify the effectiveness of our proposed method, we design the following three research questions:

RQ1: Compared with the existing classical methods, does our proposed MASE have an advantage in improving ASEE performance?

RQ2: Compared with the existing classical methods, can our proposed MASE select fewer features?

RQ3: Compared with the existing classical methods, does our proposed MASE have an advantage in computational cost?

3.1 Experimental subjects

We choose two representative datasets in our experimental studies. They are the Desharnais dataset and Maxwell dataset. These two datasets are widely used in previous ASEE research[6,8,11]. The features used to estimate software effort are mainly designed based on project complexity, the development techniques used, and the number of developers and their experience.

The Desharnais dataset includes eight numerical features and 81 projects. Four out of 81 projects have been excluded due to the missing feature values. This process results in 77 complete projects for experiments. The features’ names and their description can be summarized, as shown in Tab.1. The unit of development effort of the project is 1000 h.

Tab.1 Features used by Desharnais dataset

The Maxwell dataset includes 62 projects data from one of the largest commercial banks in Finland. The features of this dataset are described in Tab.2. Most of features are categorical. Only features Time, Duration and Size are numerical. The categorical features can be further classified into ordinal features and nominal features. Nlan and T01-T15 are ordinal features. App, Har, Dba, Lfc, Source and Telonuse are nominal features. The similarity function between different projects can be found in Section 4. The unit of development effort of the project, which is from specification until delivery, is an hour.

Tab.2 Features used by Maxwell dataset

3.2 Performance metrics

Performance metrics are essential in evaluating the performance of SEE methods. Several performance metrics have been proposed. MMRE (mean magnitude of relative error), MdMRE (median magnitude of relative error) and PRED(0.25) are the three most used metrics in previous ASEE research[6,8,11].

The MMRE metric is defined as

(1)

wherendenotes the number of projects requiring effort estimation. MREiis defined as

(2)

The MdMRE metric is defined as

MdMRE=median({MRE1,MRE2,…,MREn})

(3)

This metric returns the median value of all the MREs and it is less sensitive to outliers.

The PRED(0.25) metric is defined as below:

(4)

This metric returns the percentage of predictions that estimated effort falls within 25% of the actual effort.

Shepperd and MacDonell[16]reported that the MRE-based performance metrics (such as MMRE) is biased towards SEE methods since they have an underestimation problem. Therefore, we further consider SA (standardized accuracy) measure which is recently defined by Langdon et al[17]. SA is defined as

(5)

4 Experimental Design

In this section, we first introduce the baseline methods we want to compare, and then we show the parameters’ value of MASE and the setting of ASEE. Finally, we illustrate the validation schemas in the two datasets.

To verify the effectiveness of the proposed method, we mainly consider the following four baseline methods: The first baseline method does not consider feature selection (i.e., use original features). We use NOFS to denote this method. The second baseline method is a wrapper-based feature selection method using single objective optimization. It uses a genetic algorithm to find the optimal feature subset, which tries to optimize the performance of ASEE. We use SOFS to denote this method. The third and fourth methods are wrapper-based feature selection methods using greedy strategies. We use BSFS and FSFS to denote these two methods. In particular, FSFS starts from an empty set, and then it sequentially selects an optimal feature by using hill climbing until the performance of ASEE cannot be further improved. BSFS starts from full features, and then it sequentially removes a feature by using hill climbing until the performance of ASEE cannot be further improved. However, these two methods have a nesting effect and it will result in a local optimum. Once a feature is selected (or removed), this feature will not be removed (or selected) in the next iteration. These methods are previously used by Kirsopp et al.[7]for ASEE.

Our method MASE is proposed based on NSGA-Ⅱ[9]. Parameters name and their value used in our empirical studies are summarized in Tab.3.

Tab.3 Parameter and their value for MASE

Based on the selected feature subset by using different feature selection methods, such as baseline methods or MASE, we use ASEE to estimate the effort of each target project. In this paper, we set the number of analogies to be 3. We use the Euclidean distance to measure the level of similarity between two projects. Supposing that the feature vector for projectais {fa,1,fa,2,…,fa,n}, and the feature vector for projectbis {fb,1,fb,2,…,fb,n}. The distance of projectaand projectbcan be defined as

(6)

whereδ(fa,i,fb,i) can be defined based on the feature type (i.e., numeric, nominal, or ordinal) as below:

(7)

where maxiand minidenotes the maximal value and the minimal value of thei-th feature, respectively. Here, we can find that all the types of features are normalized into [0,1]. The used adaptation technique is the mean of the analogies.

For the Desharnais dataset, we use the validation schema suggested by Mair et al.[18]. By following their proposed splitting schema, 70% of the instances are used as the training set, and the remaining 30% of the instances are used as the testing set. This splitting process is repeated three times independently. For the Maxwell dataset, we use the validation schema suggested by Sentas et al.[19]. In particular, the 50 projects completed before 1992 form the training set, and the remaining 12 projects completed from 1992 to 1993 are used as the testing set.

5 Result Analysis

5.1 Analysis for RQ1

Since there is randomness in MASE, SOFS, BSFS, and FSFS, we carry out these methods 10 times independently and generate multiple solutions. For a fair comparison, we choose the solution which achieves best performance for the training set based on the MMRE metric. The performance comparison among different feature selection methods on the Desharnais dataset is shown in Tab.4. The best result for each metric is bolded. The results show that the MASE method can achieve better performance in most cases when considering MMRE, MdMRE, PRED(0.25) and SA metrics on each split schema. For MMRE metric, MASE can improve 26.6%, 19.3%, 22.1% and 19.3% on average when compared to NOFS, SOFS, BSFS and FSFS. For MdMRE metric, MASE can improve 28.6%, 24.6%, 20.8% and 25.2% on average when compared to NOFS, SOFS, BSFS and FSFS. For PRED(0.25) metric, MASE can improve 35.4%, 25%, 42.6% and 25% on average when compared to NOFS, SOFS, BSFS and FSFS. For SA metric, MASE also achieves the best performance.

Tab.4 Comparison among different feature selection methods on the Desharnais dataset

To further analyze the MRE values according to the testing set, we show the box plot of MRE values for each project on the Desharnais dataset in Fig.1. Our proposed method MASE has a lower median value and smaller inter-quartile range of the MRE values.

Fig.1 The box plot of MRE values for different feature selection methods on the Desharnais dataset

The performance comparison among different feature selection methods on Maxwell dataset is shown in Tab.5. The results show that the MASE method can also achieve better performance when considering MMRE, MdMRE, PRED(0.25) and SA metrics. For MMRE metric, MASE can improve 18.9%, 28.6%, 26.8% and 14.3% on average when compared to NOFS, SOFS, BSFS, and FSFS. For MdMRE metric, MASE can improve 21.9%, 43.2%, 28.6% and 30.6% on average when compared to NOFS, SOFS, BSFS and FSFS. For PRED(0.25) metric, MASE can improve 51.5%, 100%, 19% and 51.5% on average when compared to NOFS, SOFS, BSFS and FSFS. For SA metric, MASE also achieves the best performance.

Tab.5Comparison among different feature selection methods on the Maxwell dataset

MethodMMREMdMREPRED(0.25)SAMASE0.300.250.500.66NOFS0.370.320.330.37SOFS0.420.440.250.29BSFS0.410.350.420.12FSFS0.350.360.330.52

Then, we show the box plot of MRE values for each project in the testing set on the Maxwell database in Fig.2. From this figure, we can find that our proposed method MASE has a lower median value of the MRE values.

Fig.2 The box plot of MRE values for different feature selection methods on the Maxwell dataset

5.2 Analysis for RQ2

In this subsection, we analyze the number of selected features for different feature selection methods. The result of the Desharnais dataset in three different split schemas can be found in Tab.6 and the result of the Maxwell dataset can be found in Tab.7.

Tab.6Number of selected features in three split schemas for the Desharnais dataset

MethodMASESOFSFSFSBSFSSplit schema 11235Split schema 21226Split schema 31224

Tab.7 Number of selected features for Maxwell dataset

From these two tables, we can find that our proposed method MASE can select fewer features (i.e., 1 to 2 features) when compared with the baseline methods. To further analyze the selected features, we can find that: For the Desharnais dataset, PointsNonAjust feature is frequently selected; for the Maxwell dataset, Duration and Size features are frequently selected.

5.3 Analysis for RQ3

In this subsection, we mainly analyze the running time for different feature selection methods. All the methods are implemented by using the Weka package. These methods are run on Win 10 operation system (Intel i7-6500U CPU with 8 GB of memory). The results on the Desharnais and Maxwell datasets are shown in Tab.8. From this table, we can find that the running time of SOFS is the highest and the running time of BSFS is the lowest. Our proposed method MASE has similar running time with FSFS and the running time of these two methods is between that of method SOFS and BSFS. In this table, the maximum execution time of MASE is 7 061 ms and this time is acceptable. Moreover, from the RQ1 and RQ2 analysis, using MASE can help to achieve better performance by selecting fewer features.

Tab.8Time needed to select feature subset for Desharnais and Maxwell datasets

MethodDesharnais 1Desharnais 2Desharnais 3MaxwellMASE277263284334SOFS3273553687 061BSFS635158261FSFS252269267372

5.4 Discussion

In addition to the Desharnais and Maxwell datasets used by previous studies[6,8,11], to show the generality of our empirical results, we additionally choose two datasets (i.e., NASA93[13]and usp05[20]) from the promised repository. Some datasets are not used since they have few projects or features. Then, we consider the same experimental design used for the Desharnais dataset. Due to the limit of paper length, the considered metrics and characteristics of these datasets can be found in Refs.[13,20]. The comparison results of these two datasets can be found in Tab.9 and Tab.10. The best result for each metric is bolded. Final results also verify the competiveness of the proposed MASE method.

Tab.9 Comparison among different feature selection methods on NASA93 dataset

Tab.10 Comparison among different feature selection methods on usp05 dataset

5.5 Threats to validity

In this subsection, we mainly discuss the potential threats to the validity of our empirical studies. Threats to external validity are about whether the observed experimental results can be extended to other subjects or not. To guarantee the representative of our empirical subjects, we choose the Desharnais and Maxwell datasets which have been widely used by other researchers[6,8,11]. Moreover, we also choose another two datasets[13,20]to verify the generality of the empirical results. Threats to internal validity are mainly concerned with the uncontrolled internal factors that might have influence on the experimental results. To reduce this threat, we implement all the methods following the method description and use test cases to verify the correctness of our implemented MASE and other baseline methods. Moreover, we use advanced third-party libraries, such as Weka package. Threat to constructing validity is about whether the performance metrics used in the empirical studies reflect the real-world situation. We used MMRE, MdMRE, and PRED(0.25) to evaluate the performance of the prediction model. These performance metrics have been widely used in current ASEE research[6,8,11]. Moreover, we also compare our method using SA measures[16-17].

6 Conclusion

In this paper, we propose a wrapper-based feature selection method MASE using multi-objective optimization to improve the performance of ASEE. Empirical results based on projects from the real world show the competitiveness of our proposed method. In the future, we plan to extend our research in several ways. First, we want to consider more commercial projects or open-source projects in Github[21]to verify whether our conclusion can be generalized. Secondly, we want to consider other multi-objective optimization algorithms for MASE, such as SPEA[22]. Finally, we want to conduct a sensitivity analysis to analyze the influencing factors in our proposed method, such as the number of analogies.