A weighted selection combining schemefor cooperative spectrum prediction in cognitive radio networks

Li Xi Song Tiecheng Zhang Yueyue Chen Guojun Hu Jing

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

Abstract：A weighted selection combining (WSC) scheme is proposed to improve prediction accuracy for cooperative spectrum prediction in cognitive radio networks by exploiting spatial diversity. First, a genetic algorithm-based neural network (GANN) is designed to perform spectrum prediction in consideration of both the characteristics of the primary users (PU) and the effect of fading. Then, a fusion selection method based on the iterative self-organizing data analysis (ISODATA) algorithm is designed to select the best local predictors for combination. Additionally, a reliability-based weighted combination rule is proposed to make an accurate decision based on local prediction results considering the diversity of the predictors. Finally, a Gaussian approximation approach is employed to study the performance of the proposed WSC scheme, and the expressions of the global prediction precision and throughput enhancement are derived. Simulation results reveal that the proposed WSC scheme outperforms the other cooperative spectrum prediction schemes in terms of prediction accuracy, and can achieve significant throughput gain for cognitive radio networks.

Keywords：cognitive radio network; cooperative spectrum prediction; genetic algorithm-based neural network; iterative self-organizing data analysis algorithm; weighted selection combining

Cognitive radio (CR) has been viewed as a promising technology to alleviate the spectrum scarcity problem. Secondary users (SUs) are allowed to opportunistically access the licensed channels allocated for the primary users (PUs) to improve spectrum utilization efficiency. Spectrum sensing is an essential functionality of the SUs to timely detect spectrum holes for data transmission. In the interweave mode, the licensed channels can only be accessed by the SUs when they are sensed to be in an idle state, otherwise, the SUs should wait until spectrum holes are detected. However, the incapability of spectrum sensing to eliminate false alarms due to interference will reduce spectrum sensing efficiency and waste available spectrum resources[1]. To tackle this shortcoming, spectrum prediction has been proposed as an effective approach to help weaken the impact of improper spectrum detection by providing the dependable knowledge of available licensed channels.

Spectrum prediction in CR mainly targets channel availability, i.e. predicting whether the licensed channel is idle or busy. Various types of machine learning techniques have been adopted in spectrum prediction, and neural network (NN)[2]has in particular received much attention due to its good nonlinear quality, high fitting accuracy, fully distributed storage structure and the hierarchical quality of the model structure. A wavelet neural network (WNN)[3]has been studied to show that the nature of discrete transform can help build a more accurate prediction model with less complexity. Channel estimation in predictive modeling scenarios and multi-secondary-user scenarios has been investigated by using two types of artificial neural networks (ANNs)[4]. Apart from the “hard decision” models, a “soft decision” model[5]for spectrum prediction based on back-propagation (BP) neural networks has also been studied. Since the parameters of NN, i.e., weights and biases, are determined by gradient search algorithms and are sensitive to initial values, the genetic algorithm (GA)[6]has been employed to solve the problem that the NN-based spectrum prediction models are always trapped in local optimal solutions.

Based on various types of local spectrum prediction techniques, the design of cooperative spectrum prediction schemes with high prediction accuracy has attracted more and more attention recently[7]. A spectrum prediction scheme has been proposed based on the coalitional game theory[8]. It shows an outstanding performance of cooperative spectrum prediction but lacks the detailed analysis of the relationship between SUs’ characteristics and cooperative spectrum prediction performance. Cooperative spectrum prediction has been analyzed in both pre-fusion and post-fusion scenarios[9]. TheM-out-of-Nrule has been extended for cooperative spectrum prediction in this paper and the results show that cooperative spectrum prediction can lead to a significant improvement in prediction accuracy.

However, to the best of our knowledge, the existing works have not considered the heterogeneity of predictors for combination. To this end, we propose an efficient weighted selection combining (WSC) scheme for cooperative spectrum prediction, by selecting a subset of predictors for optimal combination according to the priority of each predictor, and present an analysis of the scheme in terms of both prediction precision and throughput enhancement. The mean prediction precision of the WSC scheme is simulated against traffic intensity and compared with other combining schemes to show its outstanding effectiveness. It can also be proven that the WSC scheme can provide evident throughput enhancement from both the analysis and simulation results.

1 System Model

A time slotted system with one PU andNpairs of secondary transceivers is assumed in this paper. SUs are randomly distributed around the PU, and opportunistically access the licensed channel for data transmission. PU traffic on the licensed channel is assumed to follow a Poisson process, and the ON (busy) and OFF (idle) times of the channel are drawn from geometric distributions. When the ON and OFF times of the channel are, respectively, denoted bytONandtOFF, the traffic intensity can be calculated by[2]

(1)

LetH1represent the ON state andH0represent the OFF state. The probability of the licensed channel being busy and idle can be, respectively, estimated by

P(H1)=ρ

(2)

P(H0)=1-ρ

(3)

(4)

(5)

(6)

In centralized cooperative spectrum sensing, all the participating SUs send their spectrum sensing results to the fusion center (FC) for combination, and the final results will be sent back as a guide for action. Thus, a cloud computing unit[11]is disposed at the FC to provide storage for the spectrum sensing results and computational capacity. Since the prediction duration is comparable with the sensing duration[12], we redesign the frame structure as a three-phase frame structure as shown in Fig.1. During the spectrum prediction and spectrum sensing phase, spectrum prediction is performed at the FC based on the historical sensing results. Meanwhile, local spectrum sensing is performed by SUs. Afterwards, the FC collects all the sensing results from participated SUs and makes final decisions according to the cooperative prediction results and cooperative sensing results in the reporting phase. Finally, if the licensed channel is decided to be idle, data transmission is performed by a selected SU during the data transmission phase; otherwise, no SU is allowed to transmit on the licensed channel.

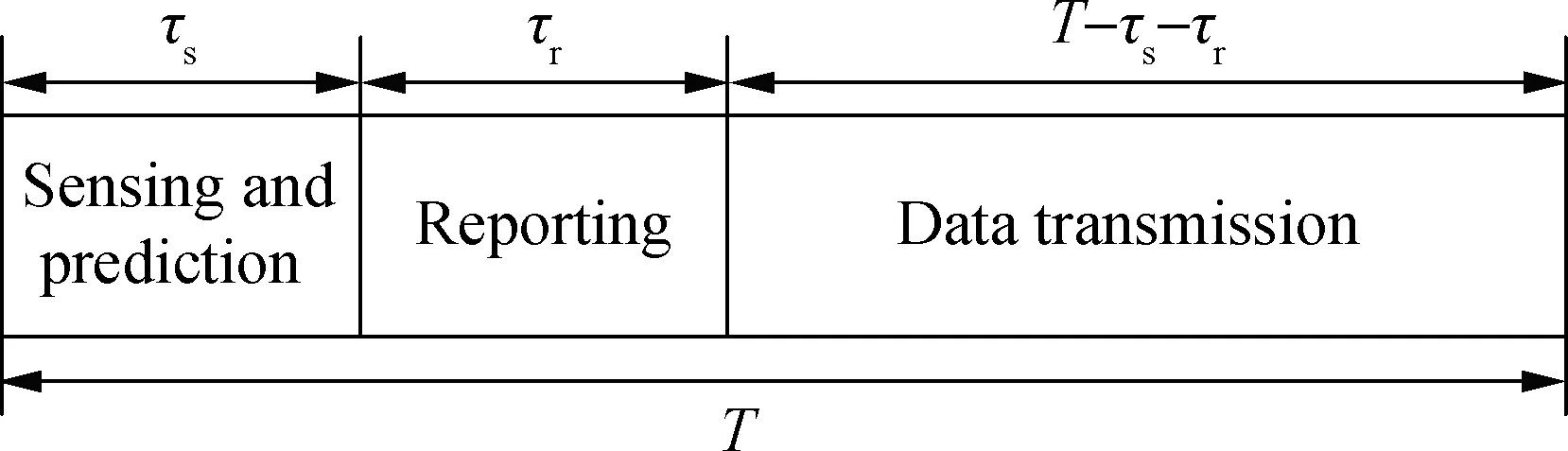
Fig.1 Three-phase frame structure

2 Cooperative Spectrum Prediction

2.1 Design of the WSC scheme for cooperative spectrum prediction

In this section, we propose a WSC scheme for cooperative spectrum prediction by selecting a subset of local predictors for optimal combination according to the reliability of each predictor, and analyze the performance of the proposed scheme. The scheme consists of three parts as shown in Fig.2.NGANN-based predictors are designed for local spectrum prediction in the first part. An ISODA-

Fig.2 The structure of WSC scheme

TA-algorithm-based fusion selection unit is designed to choose a subset of predictors for combination in the second part. A data fusion unit is designed to make optimal weighted combination in the third part.

2.1.1 GANN-based predictors

The GA is an evolutionary algorithm which applies the search principles of natural evolution for parameters optimization[13]. It is used to initialize the weights and biases of the NN in this paper since the accuracy of prediction is sensitive to the initial values. The main steps of the GA-based parameter initialization are given as follows:

1) Each set of weights and biases is encoded as a string to denote a specific chromosome, and a population of chromosomes is created.

2) The fitness value of each chromosome is calculated by the mean absolute error (MAE) as

(7)

3) Genetic operations of selection, crossover and mutation are performed among individuals to generate the next generation of chromosomes.

4) The generated offspring replace their parents in the initial population. They are decoded back into weights and biases as the result of parameter initialization.

(8)

(9)

wherex=-1 denotes that the real-state of the licensed channel is idle, andx=1 denotes that the real-state of the licensed channel is busy.

Therefore, the prediction precision of thej-th GANN-based predictor can be calculated by

(10)

After training and testing, the GANN-based predictors are established and then they can be used to perform spectrum prediction. By presenting the latestt0-length spectrum sensing results of thej-th SU to the predictor, the spectrum prediction result is obtained for each frame.

2.1.2 ISODATA-algorithm-based fusion selection unit

2) TheN+1 vectors in the clustering pattern are clustered by using the ISODATA algorithm. The clustering resultck(l) denotes whether or not thek-th predictor is clustered together with the PU in thel-th clustering round, and is recorded by

(11)

whereukdenotes the cluster thek-th vector is assigned to, anduN+1denotes the cluster the PU is assigned to.

3) Suppose that the clustering process is performed forNsrounds, andNsis large enough. The clustering frequency which denotes the frequency of each predictor being clustered together with the PU can be calculated by

(12)

4) Sort the clustering frequency of all the predictors in a descending order, and select the firstKpredictors for further combination.

2.1.3 Reliability-based weighted combination unit

To make full use of the diversity among different predictors, a reliability-based weighted combination scheme is employed. In this scheme, the weighting factor for each selected predictor represents its contribution towards the global prediction decisions. The weighted combination rule in this paper is considered as[16]

(13)

To achieve the maximum cooperative spectrum prediction precision, the weighting factorαiand the correction factorβare estimated according to the likelihood ratio test (LRT) as[17]

(14)

The corresponding log-LRT can be expressed as

(15)

Suppose thatA0contains all the selected predictors whose prediction results are idle, andA1contains all the selected predictors whose prediction results are busy. Since

(16)

(17)

(18)

When a large number of predictors are selected for further combination, a Gaussian approximation of the test statisticRpin (13) can be made according to the central limit theorem. The expectations and variances of the Gaussian distribution under different hypotheses can be, respectively, expressed as

(19)

(20)

(21)

(22)

Therefore, the false-alarm prediction probability and the miss-prediction probability of the cooperative spectrum prediction process can be calculated by

(23)

(24)

The prediction precision of the proposed WSC scheme can be expressed as

Ppre=P(H0)(1-Ψp,fa)+P(H1)(1-Ψp,md)

(25)

2.2 Enhanced throughput by using the WSC scheme

(26)

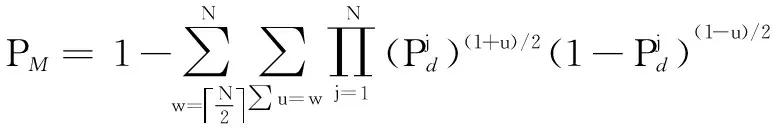
(27)

Thus, the probability distributions of cooperative spectrum prediction, cooperative spectrum sensing, and the true channel state are illustrated in Tab.1.

Tab.1Probability distributions considering true channel state,prediction, and sensing

True channel statePredictionSensingProbabilityIdleIdleIdleP1=(1-PF)P(H0)(1-Ψp,fa)IdleIdleBusyP2=PFP(H0)(1-Ψp,fa)IdleBusyIdleP3=(1-PF)P(H0)Ψp,faIdleBusyBusyP4=PFP(H0)Ψp,faBusyIdleIdleP5=PMP(H1)Ψp,mdBusyIdleBusyP6=(1-PM)P(H1)Ψp,mdBusyBusyIdleP7=PMP(H1)(1-Ψp,md)BusyBusyBusyP8=(1-PM)P(H1)(1-Ψp,md)

The cooperative spectrum sensing results can be revised by combining the cooperative spectrum prediction results to mitigate the effect of false-alarm detection, and an OR-rule is adopted. The average throughput of the proposed scheme is calculated by

(28)

(29)

(30)

To make a comparison, the normalized average throughput of the SUs when adopting the same cooperative spectrum sensing scheme without cooperative spectrum prediction is calculated by

(31)

Therefore, the throughput enhancement of the proposed scheme can be expressed as

(32)

3 Simulation Results

The performance of the proposed WSC scheme is illustrated by simulation results in this section. Three different simulations are performed based on MATLAB: 1) Investigating the prediction precision of an individual predictor; 2) The prediction precision of cooperative spectrum prediction; 3) The throughput enhancement of the WSC scheme.

In the first simulation, we evaluate the performance of the GANN-based predictor. In the parameter initialization process, the population contains 50 individuals. The iterative process of selection, crossover and mutation is performedImax100 times, where the crossover factor and the mutation factor are, respectively, set to be 0.4 and 0.2 to adjust the diversity and convergence of the population. A three-layer-NN-model with 6 neurons in the hidden layer is exploited in each predictor. The length of training/testing patterns is set to bet0=4 and the input layer of the GANN model is of the same size. Assuming that the spectrum sensing SNR of the SUs varies from -25 to 5 dB, Fig.3 shows the impact of fading on the mean prediction precision with different traffic intensities of the PU. The mean prediction precision is obtained by assuming that SU’s target probability of detection is uniformly distributed between 0.7 and 0.95. Fig. 3 shows that, for a given traffic intensityρ, the mean prediction precision increases with the enhancement of SNR, that is, a predictor can make more precise prediction based on the sensing results from SUs with a higher SNR. It is also shown that the mean prediction precision converges to |ρ-0.5|+0.5 as SNR decreases. This is because the predictor predicts the licensed channel to be always idle (ρ<0.5) or busy (ρ≥0.5) when the input patterns become quite irregular and unpredictable. In this case, the predictor can be viewed as incapable of spectrum prediction and may be abandoned for further combination.

Fig.3 Mean prediction precision of the predictor vs. SNR

Fig.4 Mean prediction precision of different schemes vs. traffic intensity

Fig.5 Normalized average throughput vs. traffic intensity

4 Conclusions

1) A genetic algorithm-based neural network (GANN) is designed to perform spectrum prediction in consideration of both the characteristics of the PU and the effect of fading.

2) A fusion selection method based on the iterative self-organizing data analysis (ISODATA) algorithm is designed to select the best local predictors for combination.

3) Considering the diversity of the predictors, a reliability-based weighted combination rule is proposed to make an accurate decision based on local prediction results.

4) A Gaussian approximation approach is employed to study the performance of the proposed WSC scheme, and the expressions of the global prediction precision and throughput enhancement are derived. Simulation results reveal that the proposed WSC scheme can provide higher prediction precision and significant throughput enhancement for any traffic intensity environment.