Availability-based maintenance optimization under unequal inspection period and imperfect repair
2018-10-17LiuYangSuChun
Liu Yang Su Chun
(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)
Abstract:Taking the multi-component system as research object, a maintenance optimization model based on the unequal inspection period and imperfect repair is established by considering the requirement of expected availability for improving the system’s availability. An age reduction factor is used to describe the effect of imperfect repair, and the modelling approach for the unequal inspection period is proposed. Unavailable situations are classified into three kinds of independent cases, and the availability is calculated accordingly. Based on the analysis of the relationship between the unavailable cases and the unequal inspection period, an optimization model under imperfect repair is established to optimize the system’s expected availability. A case study of a wind turbine is provided, and three key components, i.e. gearbox, generator and spindle, are considered. The optimization results of the unequal inspection period model and the equal inspection period model are compared. The results show that the unequal inspection period model based on availability can update the maintenance plan so as to optimize maintenance activities and improve the system’s availability.
Keywords:age reduction; inspection period; unequal period maintenance; maintenance optimization; availability
Most engineering equipment are multi-component products, such as CNC machine tools, wind turbines, construction machinery, radars, etc. For these types of equipment, the purchasing price, operation and maintenance (O & M) costs are usually high. Considering that a component’s performance will degrade gradually until a failure occurs, it is necessary to carry out reasonable maintenance to restore the system’s function. Scientific maintenance policy is crucial for maintaining the availability and reducing the O & M cost[1-2]. Besides, maintenance is also helpful to maintain and improve the availability[3].
Some studies on maintenance optimization by considering the availability’s constraint have been done. Maciejewski et al.[4]proposed an approach to estimate the system’s availability, and the Monte Carlo simulation and statistical analysis were used to verify the method. Do et al.[5]proposed a group maintenance plan for multi-component systems, where the constraint of availability was considered. Kumar et al.[6]analyzed availability via a semi-Markov process, and the stable solution of the system’s availability was obtained. In Ref.[7], a system availability model was established by using a Markov process and universal generating function, and the total maintenance cost was selected as the constraint.
Meanwhile, Moura et al.[8]adopted a semi-Markov process to evaluate the system’s availability. Based on the mixed risk rate model, Khatab et al.[9]studied imperfect preventive maintenance (PM) for mechanical systems, and an availability model was established. Wang et al.[10]established a long-term availability model, and numerical simulations were used to optimize availability under imperfect repair. Lü et al.[11]proposed an inspection policy, and a maintenance optimization model was developed. Based on the Petri nets theory, an availability model was proposed to calculate availability under different maintenance strategies in Ref.[12]. With the aim to maximize the system’s availability, Ali et al.[13]proposed a selective maintenance policy to determine the number of components to be replaced or repaired within the limited time interval. In Ref.[14], the availability and maintenance policies undergoing periodic inspections were studied for a competing-risk system. Aiming to improve the availability of a distribution system, Tiwary et al.[15]proposed an approach to optimize the inspection and repair.
In most of the above studies, the inspection and maintenance period were supposed to be equal. This is impractical because their aging speed will be accelerated with the increase of products’ usage. Thus, more frequent inspection and maintenance are needed. Up to now, studies on maintenance optimization for multi-component systems considering the unequal inspection period and availability requirements are quite limited.
In this study,an age reduction factor is introduced to describe the effect of imperfect repair, and a maintenance optimization model based on the unequal inspection period is proposed, in order to develop reasonable maintenance decision and achieve the expected system’s availability.
1 Modeling for Maintenance Optimization
1.1 Inspection policy and assumptions
For a multi-component product, it usually needs to be checked to ensure its availability. Generally, the inspection obeys the following assumptions:
1) The failure can be detected at timeti(i=1, 2, …,N), and the inspection periodTiis varied;
2) The inspection is perfect, and the possible failure can be found at the end of the inspection;
3) If a failure is found during the inspection, the component will be maintained just after the inspection, and repair timeγis a random variable;
4) The inspection timeθof each inspection is a constant;
5) Before the inspection, the system may be available or unavailable, while its state does not change during the inspection.
1.2 Age reduction
By adopting imperfect repair, the performance of a component or system can be restored to some extent. In order to describe the change of the failure rate after repair, an age reduction factor is introduced. The value of the age reduction factor is set to be [0, 1], where “0” means that the system is restored to the state of as bad as old (ABAO) and “1” means that the system is restored to the state of as good as new (AGAN). Usually, the system will be restored to somewhere between ABAO and AGAN, and the value of the age reduction factor depends on the effect of imperfect repair, as shown in Fig.1.
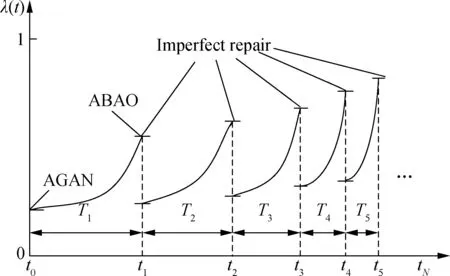
Fig.1 Failure rate and maintenance
From Fig.1, with the continuous use of a product, in order to ensure that it has high availability, the inspection period should be continuously shortened, i.e.,T1>T2>…>TN. It is assumed that there is a proportional relationship between the adjacent inspection periods, i.e.,T2=α1T1,T3=α2T2, …,TN=αN-1TN-1, the inspection periodTican be obtained as
Ti=α1α2…αi-1T1i=1,2, …,N
(1)
whereTi=ti-ti-1is thei-th inspection period, which includes working time and nonworking time;tiis the time point corresponding to thei-th inspection;αiis the age reduction factor during thei-th inspection period;Nis the total number of inspection periods.
1.3 Model of system availability
According to the above assumptions, the availability is a periodic function ofTi. By adding the effective working time during each inspection period, we can obtain the total effective working time. Thus, the system’s availability at any timex(x=t-ti-1, 0≤x≤Ti,t≥ti-1) between two inspections can be calculated based on Fig.2.
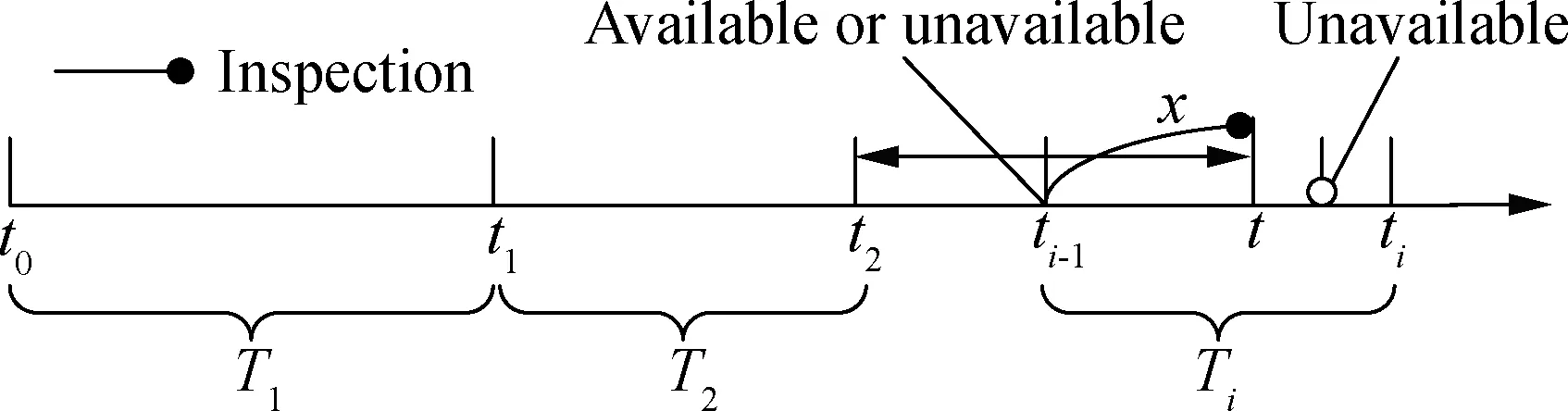
Fig.2 The inspection process of system
At operation timexwhich is started from the last inspection point, the system may be down due to the following reasons:
Case1The system is in repair. If a failure is found during the inspection and it will be maintained immediately after the inspection, the repair time isγand the inspection time isθ. Ifγ>x-θ, the system is unavailable. Thus, Case 1=(failure is found during the inspection)∩(γ>x-θ), as shown in Fig.3(a).
Case2The system has failed, while the failure has not been found. It can be further divided into the following two subcases:
Case2.1Case 2.1=(no failure is found during the inspection) ∩ (a failure occurs during thex-θperiod after the inspection), as shown in Fig.3(b).

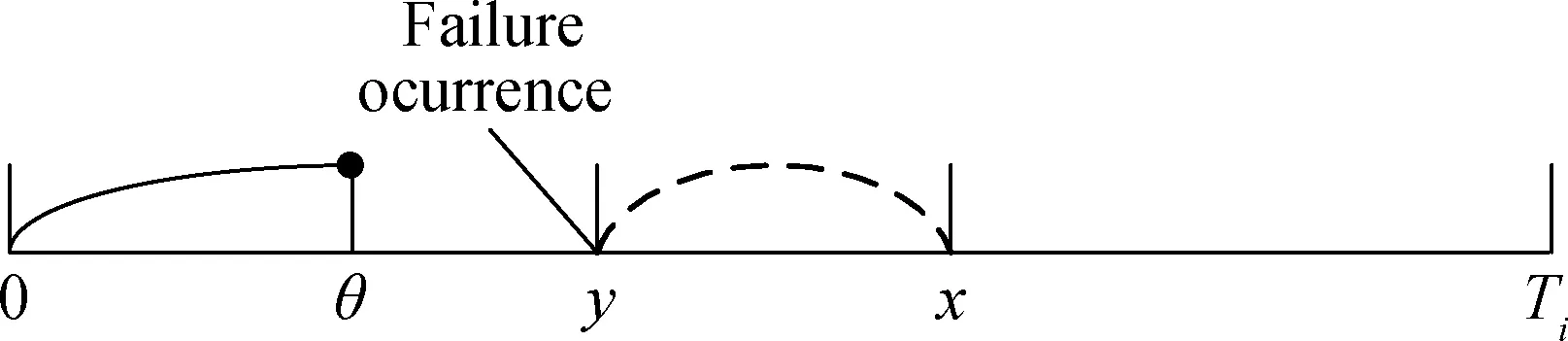
(b)
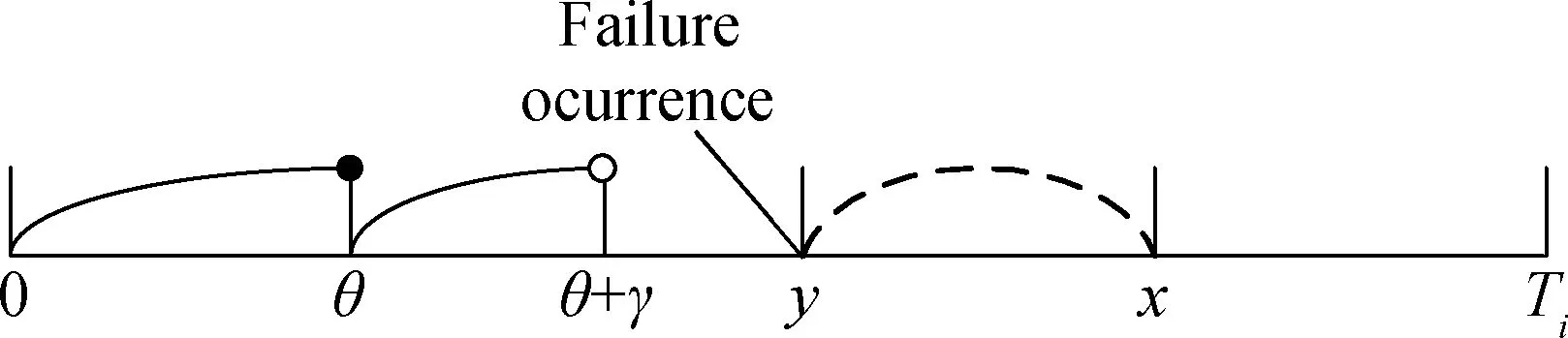
(c)
Case2.2The failure is found during the inspection and repaired immediately after the inspection, and the repair is completed at timey(θ≤y≤x). After this, the system fails again during thex-yperiod. Thus, Case 2.2=(failure is found during the inspection)∩(the repair is finished at timey)∩(failure occurs again duringx-yperiod), as shown in Fig.3(c).
Case3The system is in the process of inspection. Case 3=(θ≥x), as shown in Fig.3(d).
Case 1, Case 2 and Case 3 are independent of each other. Therefore, the instantaneous unavailability of the system at timexcan be expressed as
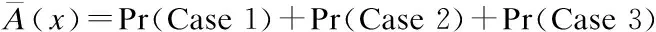
(2)
where Pr(·) is the probability of each case that causes the system unavailable.
On the basis of assumptions 2) and 5), we can obtain
(3)
(4)
wherep1is the probability that the system is unavailable before the inspection;p2is the probability that the system is unavailable if the failure is found during the inspection;βis the probability of failure caused by the inspection.
Thus, the probability of all the cases that cause the system unavailable is as
(5)
(6)

(7)

With Eqs.(1) to (7), the system’s unavailability at timexis obtained as
(8)

(9)
The instantaneous availability of the system at timexcan be expressed as

(10)
If the failure inspection period isTi, the expected system’s availabilityAE(Ti) during thei-th inspection period can be calculated by
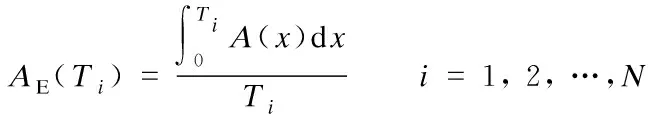
(11)
The expected system’s availabilityAE(Td) within a finite timetdcan be expressed as
(12)
In order to make the actual maintenance more convenient and efficient, we use the average value of the age reduction factor within the entire life of the system to replaceαi, as follows:
(13)
All the subsequent inspection periods can be expressed with the first inspection periodT1, as follows:
(14)
Thus, the objective function and constraints of the availability-based maintenance optimization are as

(15)
2 Case Study


Tab.1 Parameters of the components
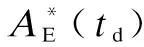

Tab.2 Optimization results

Fig.4 The expected availability of the components
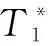
From Fig.4, we find that the above three curves have a similar trend. The expected availabilityAE(td) increases rapidly until it reaches the peak, and then it decreases gradually. WhenT1is small, the inspection is frequent, which results in a longer inspection time. When the inspection is carried out, the system is in a state of shutdown. Thus, whenT1is small,AE(td) is low. With the increase ofT1,AE(td) increases. The system can achieve maximum availability when the downtime caused by inspection is balanced with the downtime due to failure. AsT1increases, the system’s downtime caused by failure also increases gradually, and it results in a downward trend for system availability. We can also find that the increase of expected availabilityAE(td) with a low failure rate is faster than that with a high failure rate, i.e., spindle>generator>gearbox. Furthermore, the decline ofAE(td) for the component with a low failure rate is obviously slower than that with a high failure rate, i.e., spindle Tab.3 Instantaneous availability under From Tab.3, for all three components, the maximum instantaneous availabilityAmax(ψ) is greater than 99.90%. It shows that the model has a good effect on the maintenance optimization for the components. Fig.5 shows that in the initial stage, the instantaneous availability increases sharply, and it declines after reaching its peak. Since the inspection has achieved a great success in the early stage of the system, the downtime caused by failure decreases greatly, and thus the instantaneous availability is on the rise. With the increase of the system’s running time, the system performance degrades gradually. When the inspection and performance degradation reach a balance, system availability is maximized. With the increase of operation time, the degradation of performance plays a dominant role gradually, and it results in the decrease of the availability. In addition, by comparing with Fig.4, it is found that the variation tendency of the expected availability is similar to the instantaneous availability. All of these increase during the first phase and then they will decline. Tab.4 shows the comparison of the optimization results of the two models, i.e., the model based on unequalTiand the model based on equalTi. From Tab.4, the optimal availability has some differences, and the optimization result of unequal period inspection is superior to that of equal period inspection. If the model based on equalTiis used to optimize the availability of the wind turbine’s key components, the availability of the components cannot reach the requirements of the Chinese National Standard on the wind turbine availability, 97%. As can be seen from Tab.4, the two models have advantages. The model based on unequalTican make the availability of the system as high as possible, and the number of the inspections of the model based on equalTiis less, which is beneficial to saving personnel cost. However, for complex electromechanical products such as wind turbines, due to the poor working environment, once a failure occurs, a significant cost will be incurred. It is necessary to increase the availability of wind turbines as much as possible and reduce the occurrence of failure. The effectiveness of the unequal period inspection model is proved. Tab.4 Comparison of two models 2)The research results show that the model based on the unequal inspection period proposed in this paper can improve the availability of the system better than the model based on equal inspection period, and ensure the availability of the wind turbine’s key components meet the requirements of the Chinese National Standard for wind turbine availability. It provides a theoretical basis for making a scientific and reasonable maintenance policy for a wind farm. 3) In future study, some other factors can be considered in the maintenance optimization model, including the logistics cost, and spare parts, etc. The bi-objective or multi-objective optimization model can also be considered to achieve better results. In addition, field data obtained from the supervisory control and data acquisition (SCADA) system of wind farms can be integrated into the optimization model.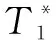


3 Conclusions
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Mathematical models for properties of mortars with admixtures and recycled fine aggregates from demolished concretes
- Damage evolution analysis of cast steel GS-20Mn5V based on modified GTN model
- Analogy-based software effort estimation using multi-objective feature selection
- A recognition model of survival situations for survivable systems
- A weighted selection combining schemefor cooperative spectrum prediction in cognitive radio networks
- Syntheses and calculation of (E)-4-chloro-4’-ethoxystilbene and (E)-4,4’-dichlorostilbene
