与阿氏圆有关的广义将军饮马问题
2018-10-16荣贺曲艺
荣 贺 曲 艺
(1.北京市顺义牛栏山第一中学 数学教研组 101301;2.北京市顺义牛栏山第一中学 数学教研组 101301)
1 知其然——问题与问题解答
题目1(2018年初中数学联赛二试(A卷)第2(2)题)如图1-1,在扇形OAB中,∠AOB=90°,OA=12,点C在OA上,AC=4,点D为OB的中点,点E为弧AB上的动点,OE与CD的交点为F.求CE+2DE的最小值.
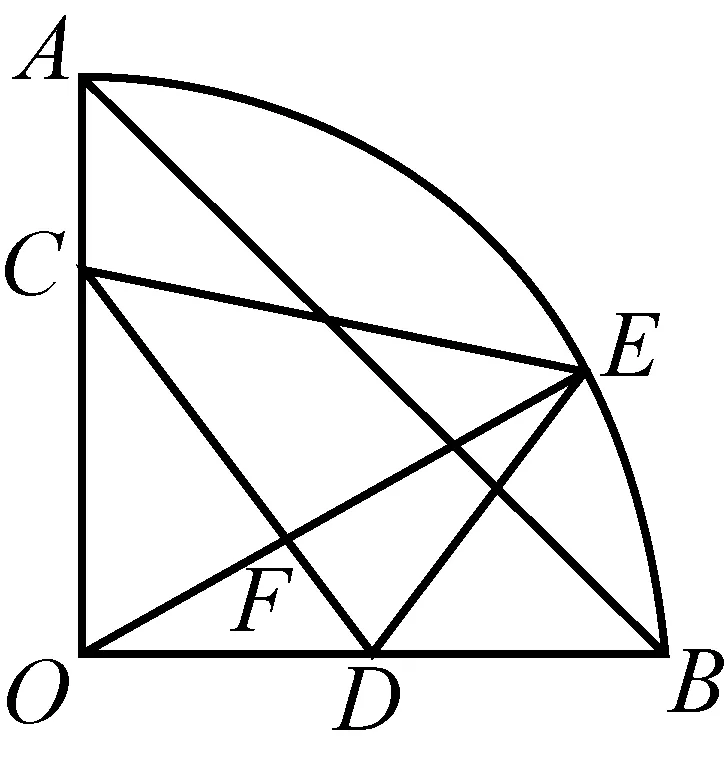
图1-1
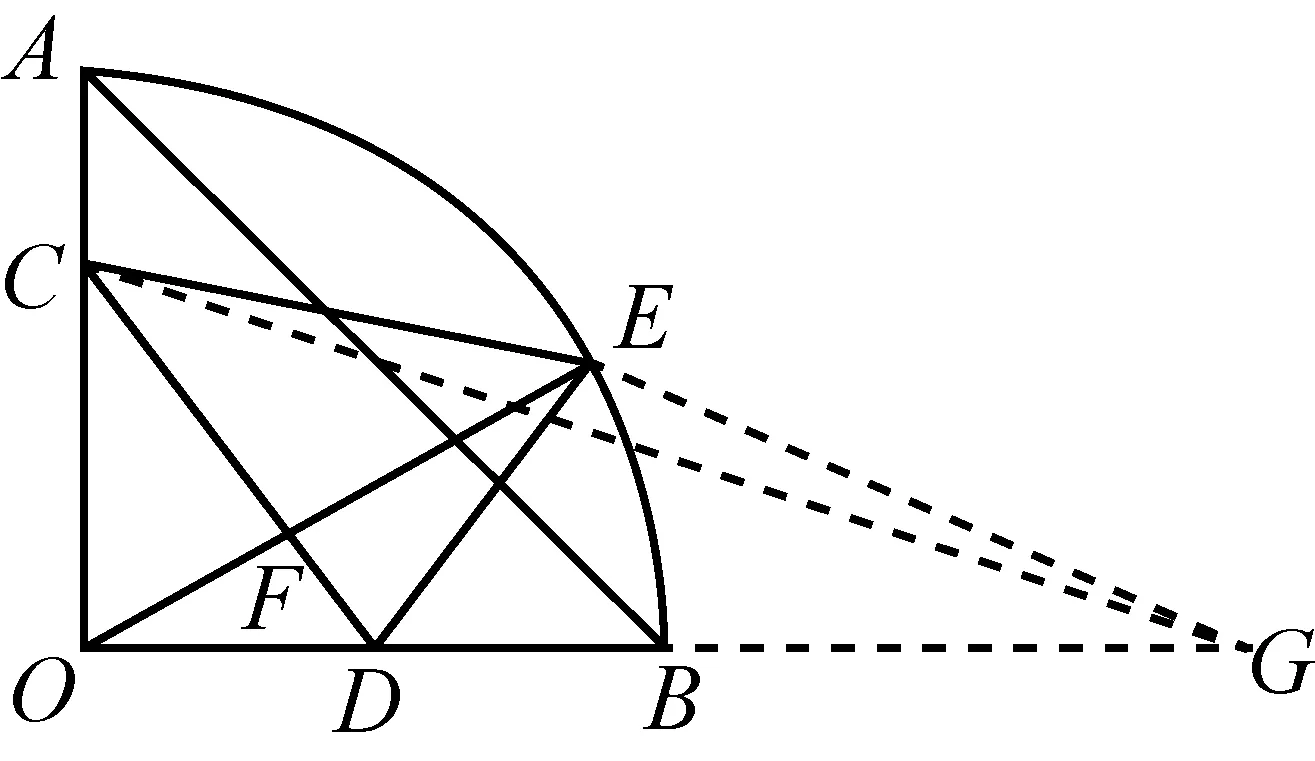
图1-2
解如图1-2,延长OB至点G,使BG=OB=12,连结GC,GE.
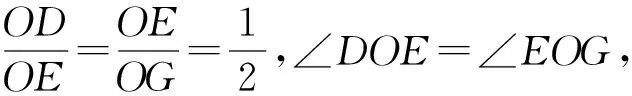
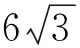
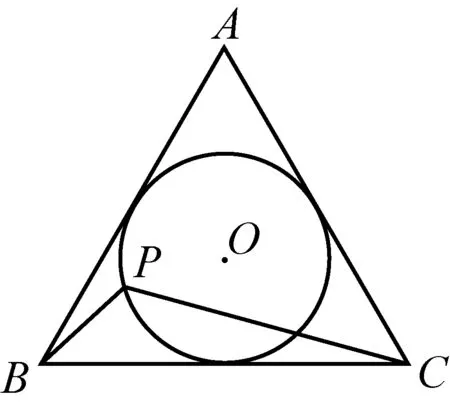
图2-1
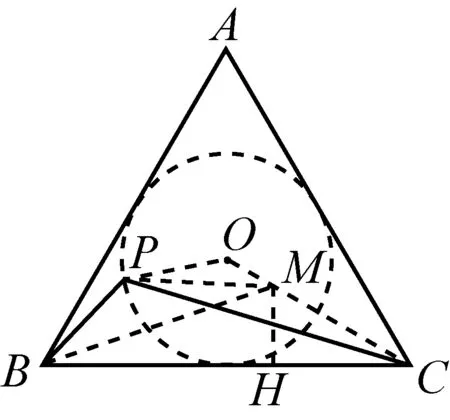
图2-2
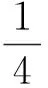
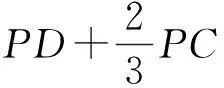
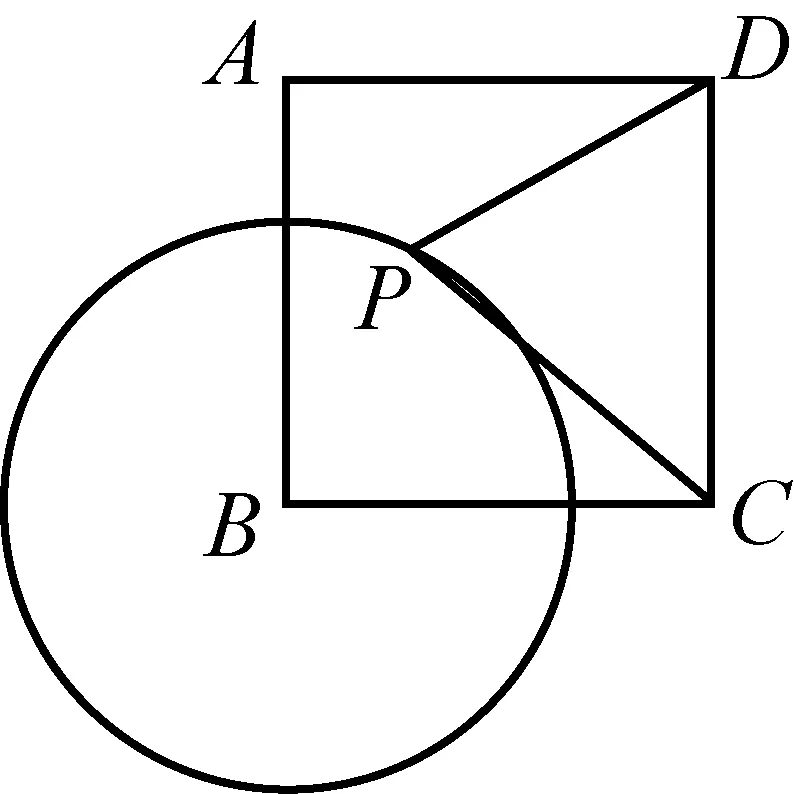
图3-1
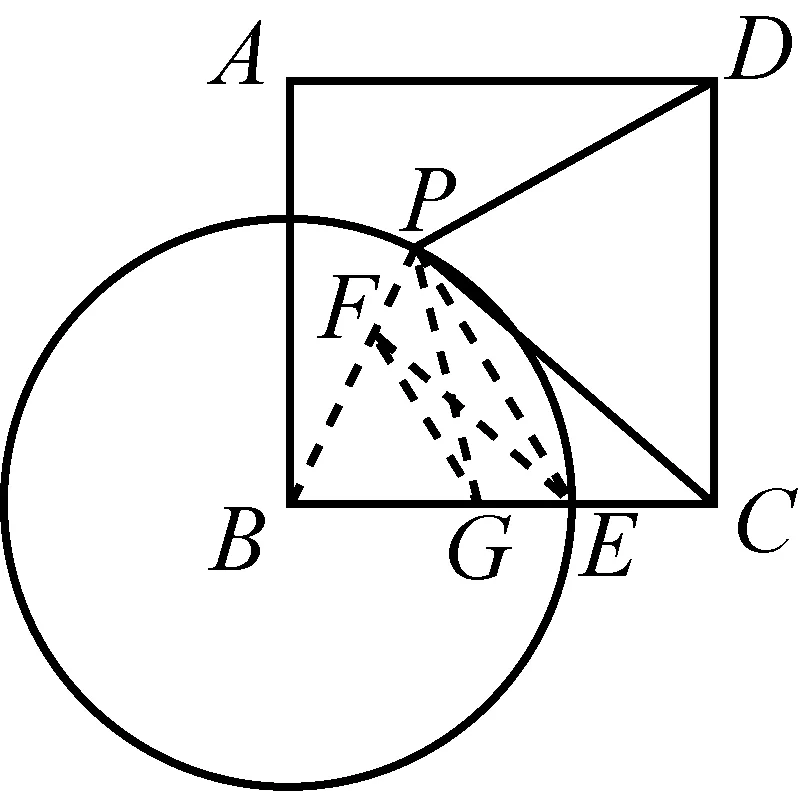
图3-2
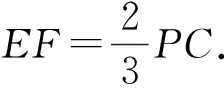
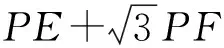
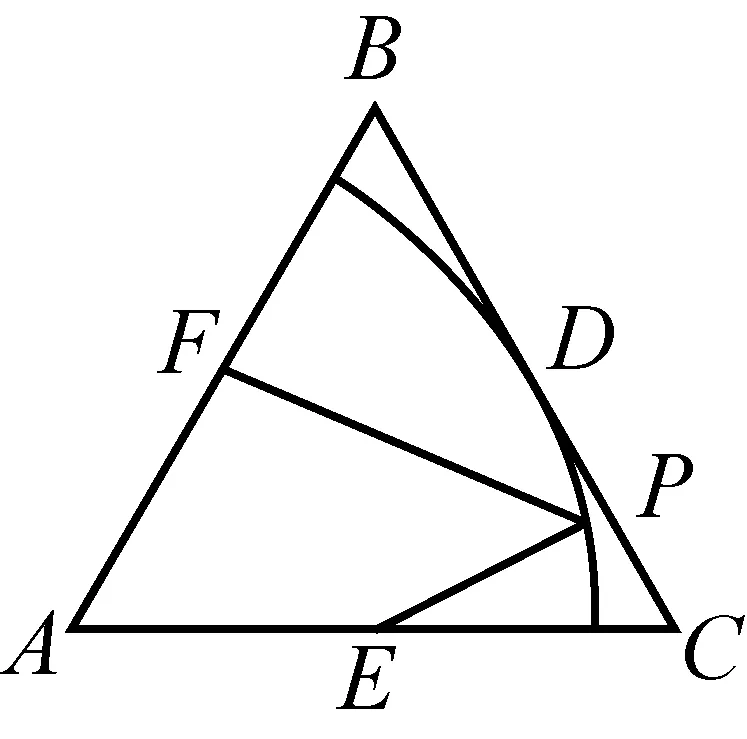
图4-1
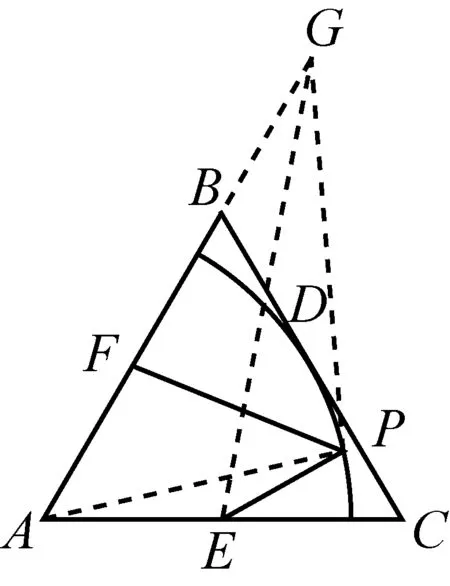
图4-2
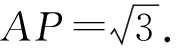
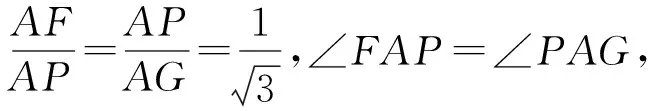
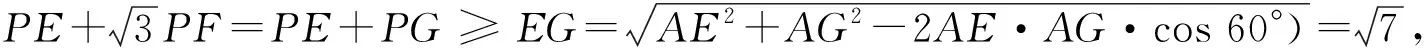
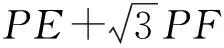
以上题目是近几年各种试卷中经常出现的一类题目,可是不少学生对此类问题还是认识不清.通过对参赛学生的了解,他们在考场上没有解答出来,而看了以上解答后,感觉确实不是难题.为什么会出现如此大的反差呢?或许这是初学者的通病,只是停留在追问“答案是什么”的层面,还没有去追问“为什么这样作答”、“凭什么想到这样作答”的层面.
本文先通过相似三角形的共边定理,理解辅助图形的构造,将型如“PA+λ·PB”的最值问题,转化为型如“PA+PC”的最值问题,进而转化为“将军饮马”问题.深究动点P的位置,引出此类问题的背景——阿氏圆,分析与理解阿波罗尼斯圆定理及性质,最后阐明此类问题的本质.并在感受“知其然”的基础上,还要“知其所以然”和“知何由以知其所以然”.
2 知其所以然——辅助图形的构造
为了能更好的引导学生处理这类问题,认清题目考察的知识与能力,下面我们需要对以上题目加以比较,寻找共同点,并总结经验,提升方法.
几何关系提取题目中的两定点A,B同在圆内或圆外,一动点P在圆周上,求型如“PA+λ·PB”的最值问题.
思路来源分析“两点之间线段最短”是处理线段和最短问题的一条重要的依据.当看到“两定点A,B在某界线的同侧”,很容易想到“将军饮马”问题,接下来处理问题的关键就是:如何将λ·PB转化为一条线段PC(即λ·PB=PC)且在界线的另一侧.而见到“λ·PB=PC”,自然联想到“相似三角形”,构造λ为比例系数即可.
首先,我们来处理“λ·PB”的转化问题.
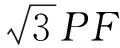
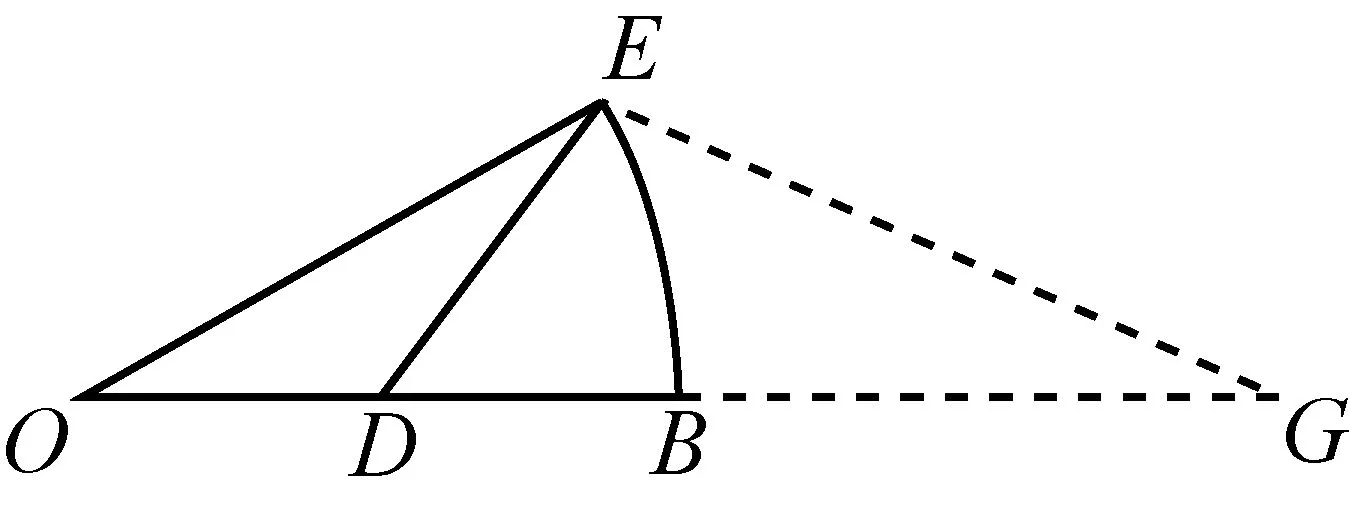
图5-1
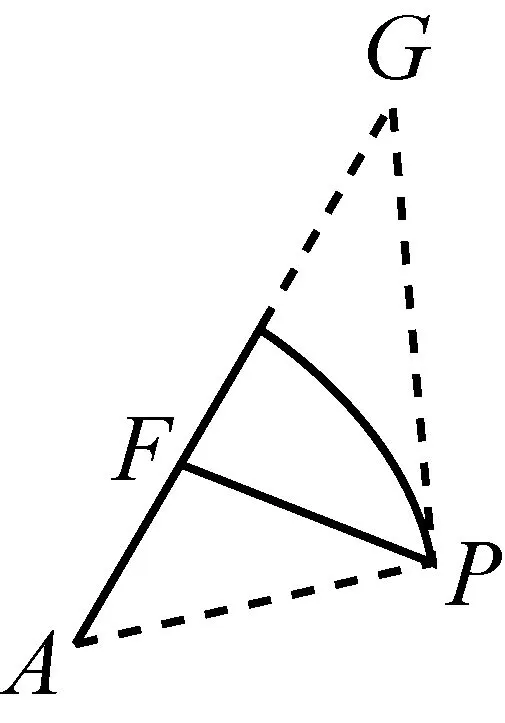
图5-2
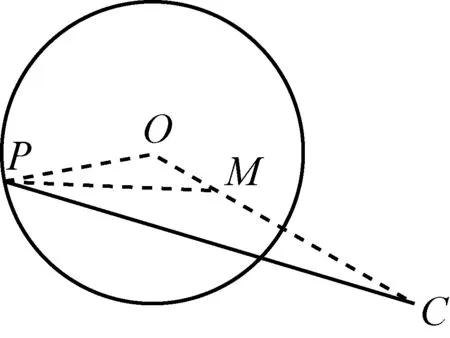
图5-3
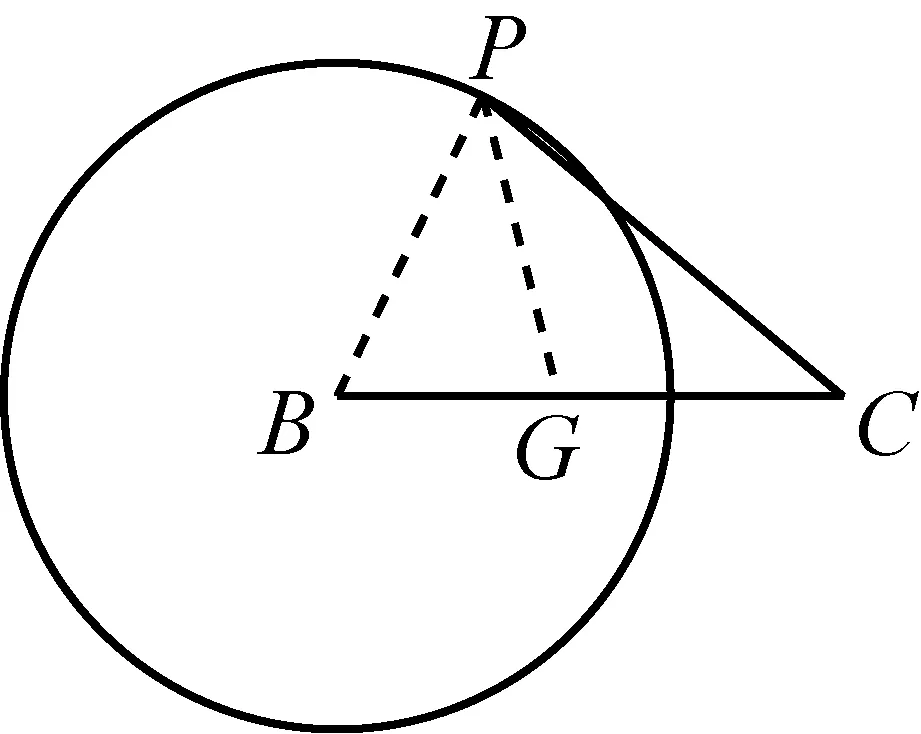
图5-4
共同点分析观察其中一个定点(D、F、C、C)的位置,结合圆的半径和此定点与圆心的距离之比恰是“系数”的特点,容易想到构造相似三角形来转化线段.上面四个图形的本质是“相似三角形的共边定理”,下面了解一下此定理,有利于我们构造此类辅助图形.
相似三角形的共边定理[3]如果有公共边和共线边的两个三角形相似,那么公共边是共线边的比例中项.用数学符号表示如下:
如图6所示,△ABP∽△APC,AP是公共边,AB和AC是共线边.则有AP2=AB·AC.
这是平面几何中的一个常见图形,由相似三角形容易得出以下三个结论:
①∠APB=∠C;②∠ABP=∠APC;③AP2=AB·AC.
在此图形中,任意两个结论都可以推出另一个结论,其形式与直角三角形中的射影定理类似,亦可称其为“广义射影定理”,或简称“共边定理”.
其次,处理两线段和的最短问题.
先来看将军饮马问题.
将军饮马问题[4]数学模型如图7-1,点P为定直线l上的一个动点,点A,B为定直线l外的两个定点.求当PA+PB的值最小时,确定动点P的位置.
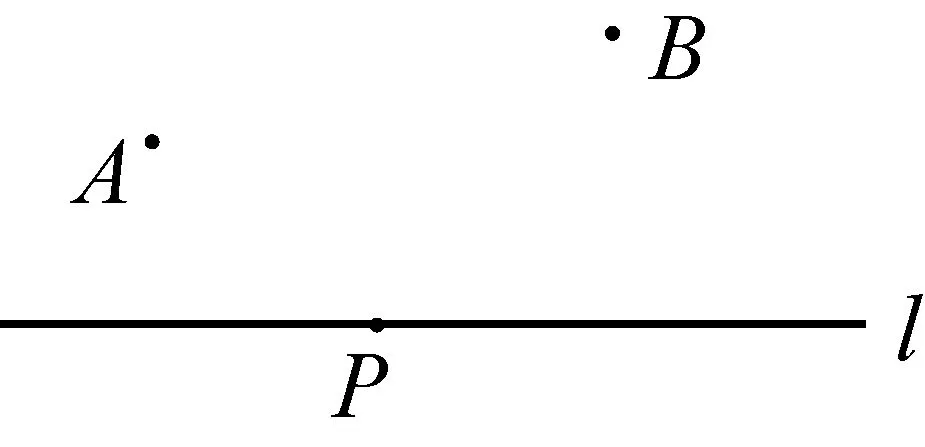
图7-1
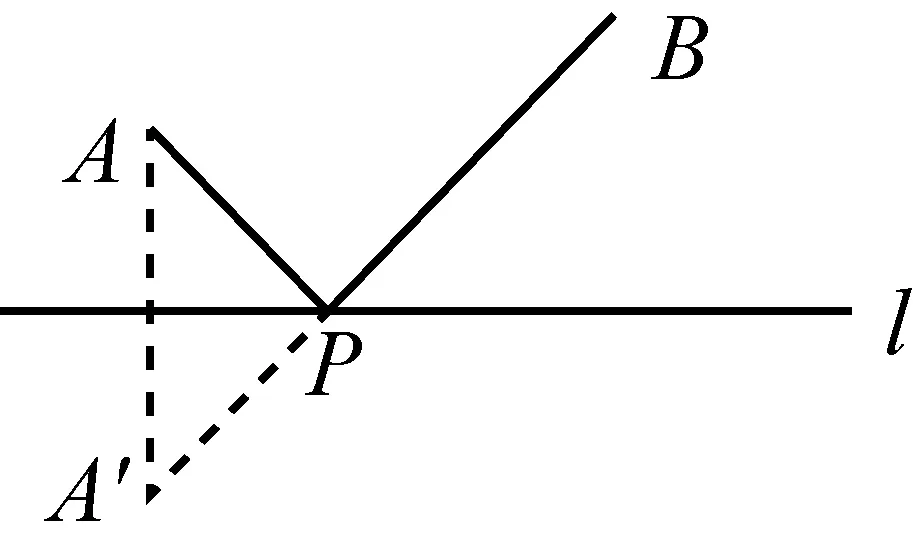
图7-2
解如图7-2,先作A关于l的对称点A′,连接A′B与l相交于P点,则PA+PB的值最小.
类比将军饮马问题,我们可以将上面四个题目中出现的圆作为广义上的“河”,“河的同侧”为圆内或圆外,这样,圆周上动点P,到圆内(或圆外)两定点A,B的距离的线性和“PA+λ·PB”的最短问题,就变成了广义将军饮马问题.
广义将军饮马问题如图8-1,8-2,点P为定圆O上的一个动点,点A,B为圆O内(或外)的两个定点.求当PA+λ·PB的值最小时,确定动点P的位置.
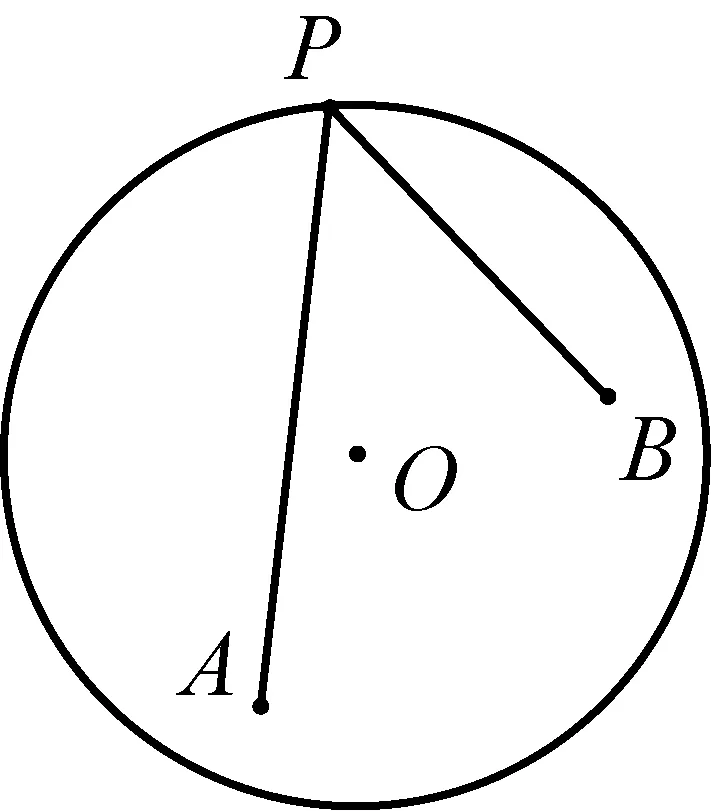
图8-1
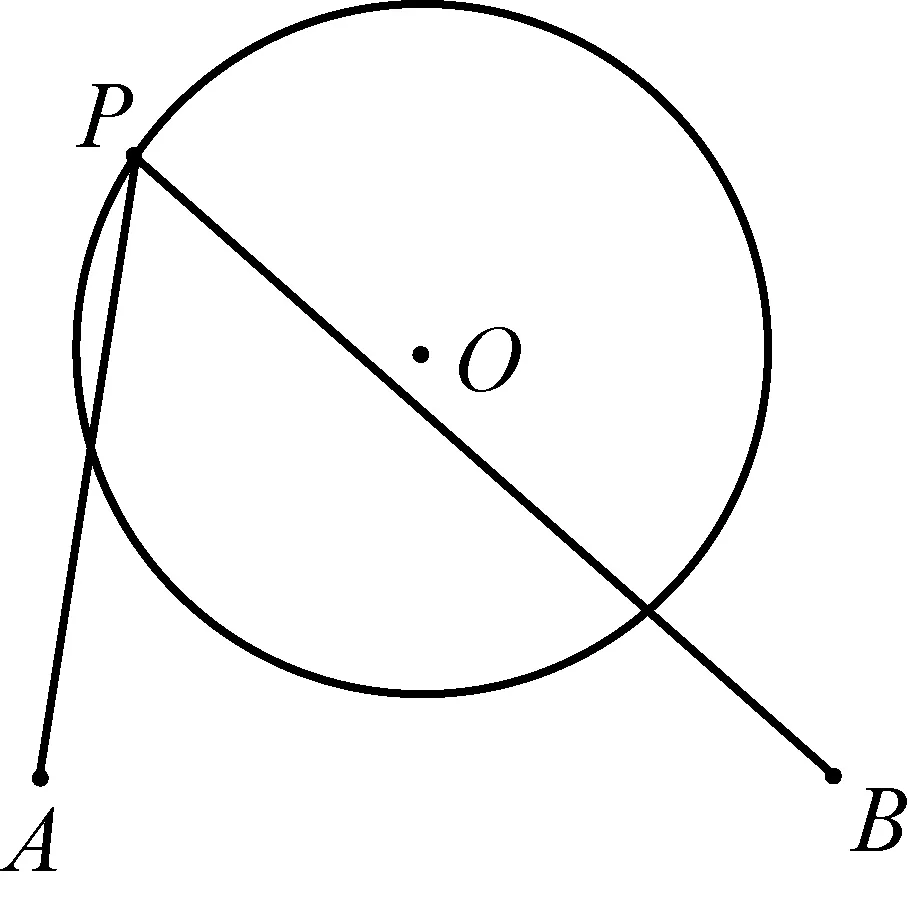
图8-2
最后,理顺一下解答思路.
遇到广义将军饮马问题,可以先利用共边定理,将系数不是1的线段转化为系数是1的线段,再利用两点之间线段最短处理即可.
3 知何由以知其所以然——命题的背景
通过上述分析,得到了解决广义将军饮马问题的一般步骤,那么,这个问题是怎么设计出来的呢?为什么这样构造辅助图形呢?我们可以进一步的追问其背景,其实在现行高中教科书[5] 中,B组练习3就是此问题的体现,问题中的圆就是阿波罗尼斯圆.下面我们来看一下阿波罗尼斯圆定理及其性质:
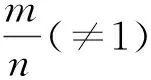
此结论为阿波罗尼斯发现的,这个圆常称为阿波罗尼斯圆,简称阿氏圆.其中A,B两点称为该阿氏圆的基点.
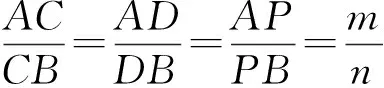
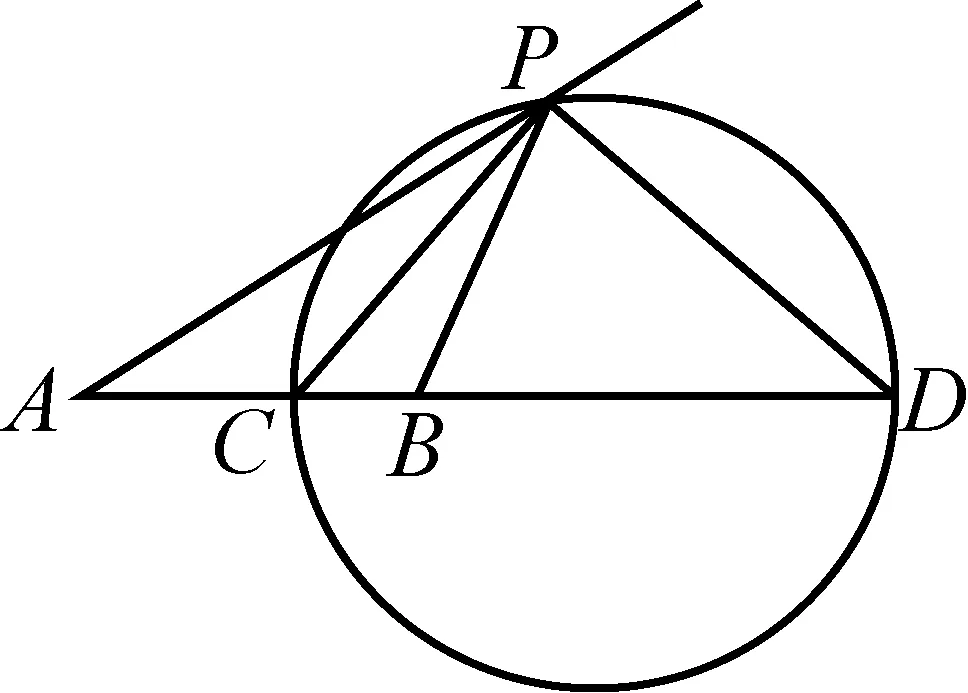
图9-1
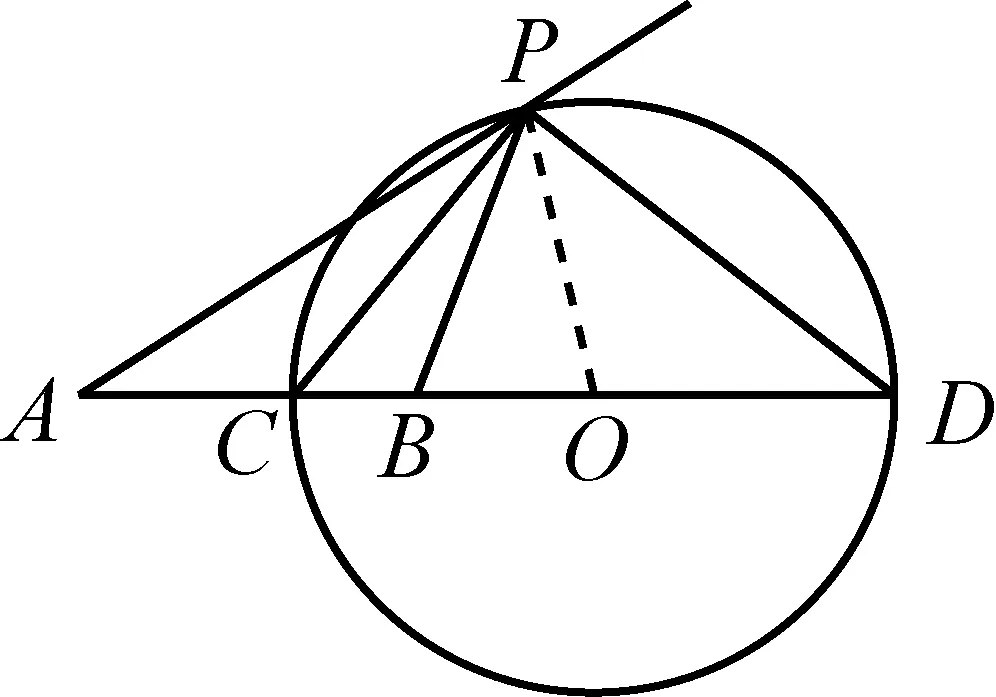
图9-2
由阿氏圆定理及其证明可得以下两个阿氏圆性质.
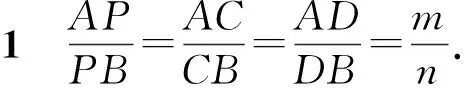
推论如图9-2,若O是阿氏圆圆心,则
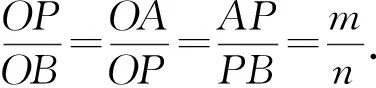
性质2内分点C对应∠APB的内角平分线;外分点D对应∠APB的外角平分线.
针对性质的应用,可参见文献[7],本文只是利用定理及性质,寻找出阿氏圆的基点,进而帮助我们作出辅助图形.
由阿波罗尼斯圆定理及性质可知结论:
(1)阿氏圆的两个基点与阿氏圆的圆心在同一条直线上;
(2)两个基点分别在阿氏圆的圆内和圆外;
(3)阿氏圆上点到两基点距离之比等于阿氏圆半径与圆心到其中一个基点距离之比.
有了以上三条结论,我们就能更顺利的解决广义将军饮马问题了.我们来看下面题目.
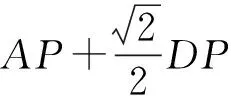
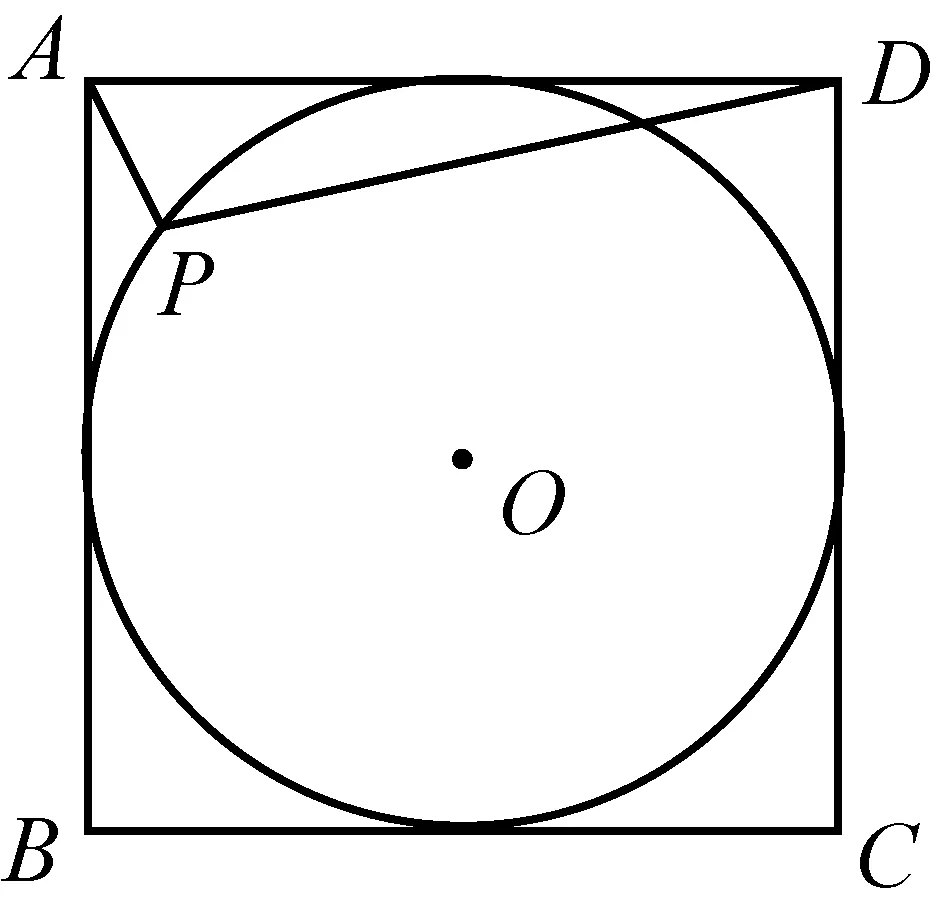
图10-1
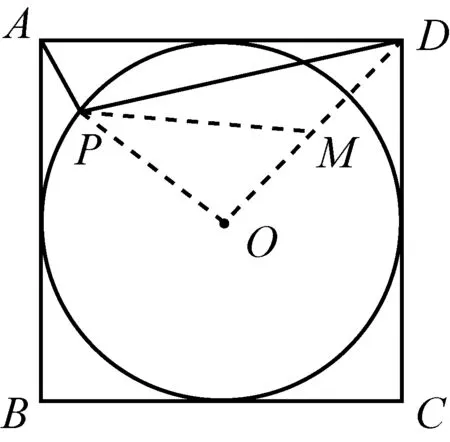
图10-2
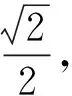
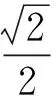
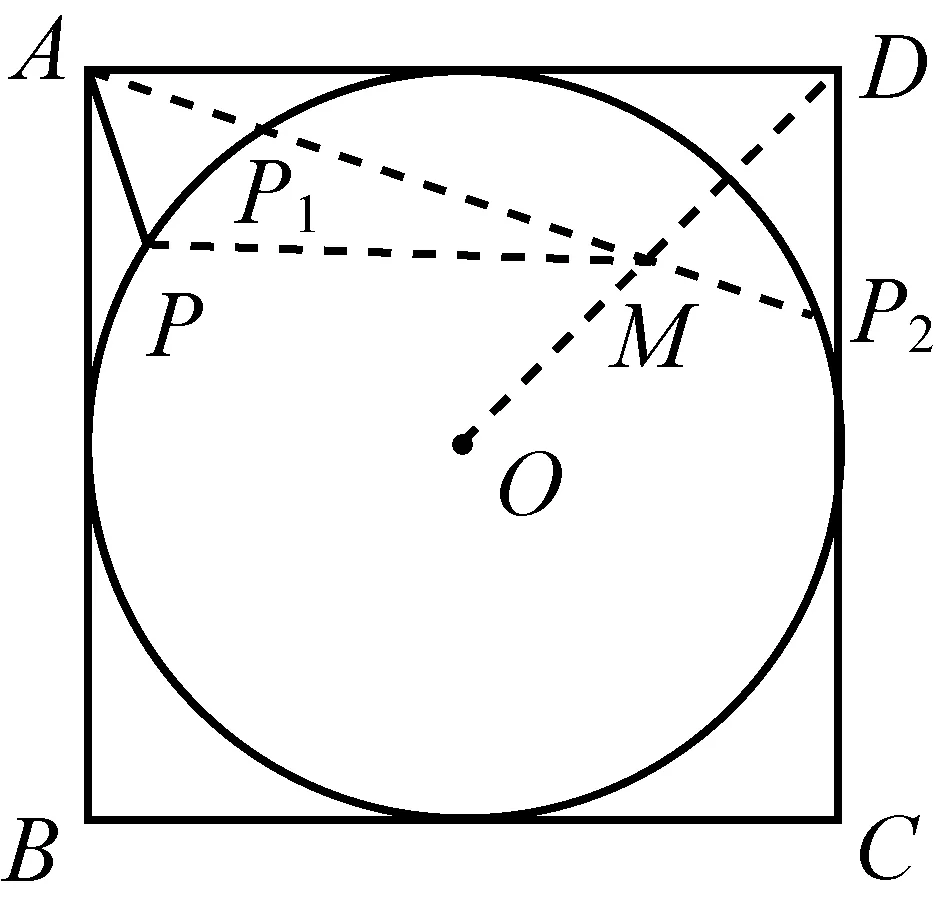
图10-3
通过以上对阿波罗尼斯圆定理的认识和简单应用,在线段的转化上有了新的手段,处理此类广义将军饮马问题也就更加容易了.
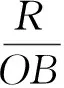
(1)两定点A,B在圆外时:
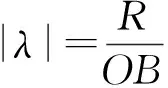
(2)两定点A,B在圆内时:
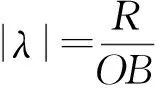
综上所述,要让圆外的基点B对应线段PB的系数|λ|<1(或圆内的基点B对应线段PB的系数|λ|>1),这样才能利用R2=OM·OB寻找另一基点M.其中,λ>0时,可求型如“AP+λ·PB”的最小值问题;λ<0时,可求型如“AP+λ·PB”的最大值问题.而当λ=±1时,显然结论平凡.
下面请看例题感受一下.
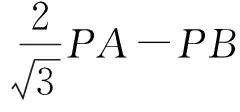
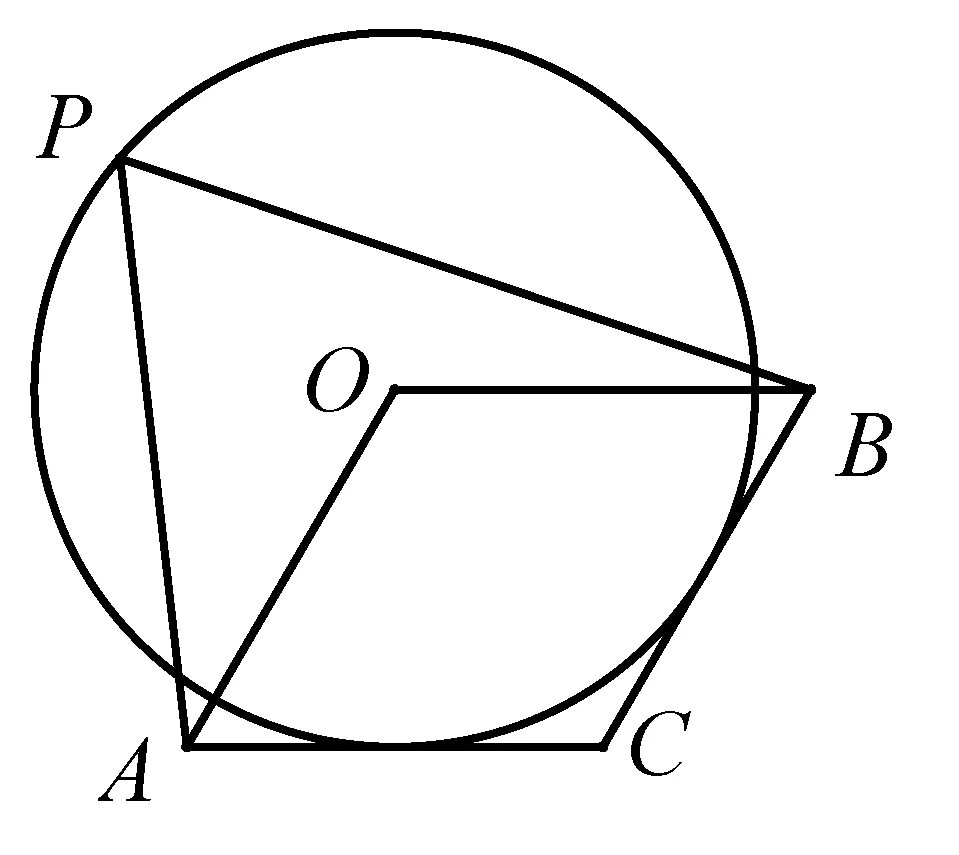
图11-1
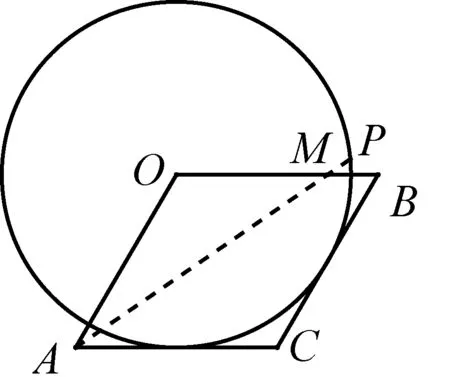
图11-2
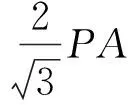
题目7(2018年初中数学联赛二试2题改编)如图12-1,在扇形OAB中,∠COD=90°,OC=12,点B在OD上,BD=4,点A为OC的中点,点P为弧CD上的动点.求2PA+3PB的最小值.
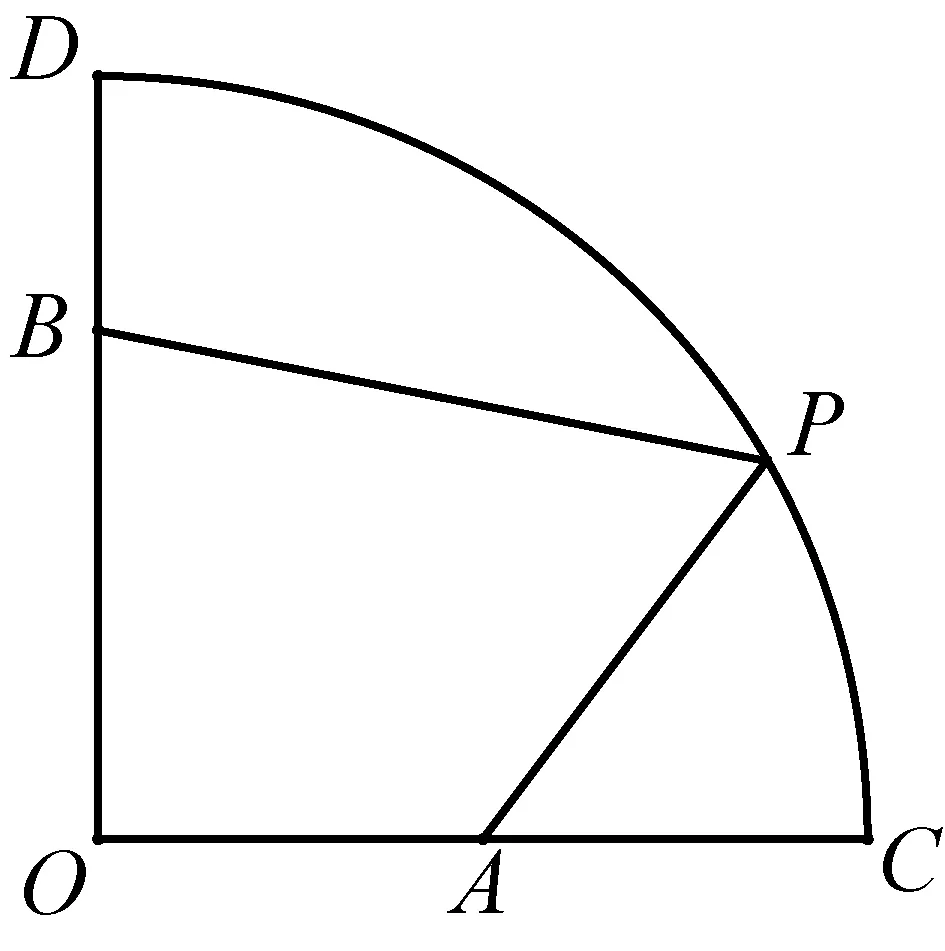
图12-1
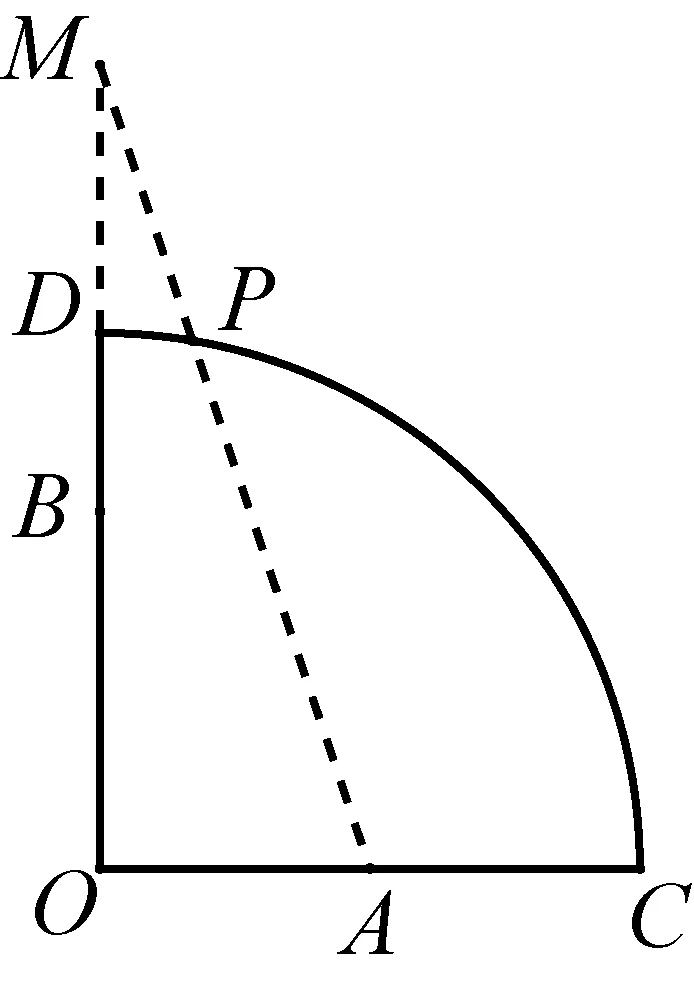
图12-2
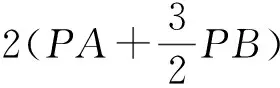
通过上述问题的分析和解答,希望对几何的学习能有所帮助,不要只是停留在“答案是什么”的层面,还需要去追问“为什么这样做”、“凭什么这样想”的层面.理解“知其然”,还要“知其所以然”和“知何由以知其所以然”.
