管窥一道试题的素养渗透

山东省单县第一中学(274300) 董文涛

新一轮高考方案的实施,其教学目标的集中于“提升学科核心素养,落实立德树人”的根本任务;而数学学科的核心素养具有数学科的基本特征与学科特色,更是涵盖促进个人终身学习与发展的关键能力和多方面的思维品质.从学科意义层面上,数学学科的核心素养体系(数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析)是落实课程教学目标的重要途径,而基于数学核心素养合适的问题情境(如试题)的解决,则是评价的重要载体.数学核心素养的独立性、整体性,且易于相互交融;使得试题是核心素养融合的一个有机整体.

试题呈现

题目(2017年新课标I卷理科第16题)如图1,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为___.

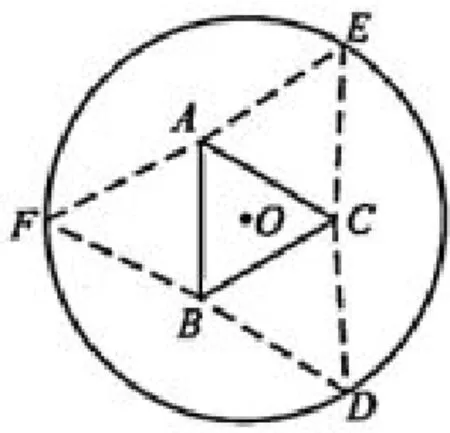
图1

一、试题简评

试题以立体几何中的翻折问题为载体,考查空间几何体与三视图、体积,函数的最值等.试题主要考查学生在转化化归的数学思想方法应用中,经历直观想象、数学建模和数学运算,完美展现四能:发现问题、提出问题、分析问题和解决问题的水平.

命题者从思想方法上高端设计考查化归思想、函数思想、数形结合思想,且兼顾考试内容的基础性、综合性、应用性和创新性,能坚持能力立意的命题原则,以体现数学学科的科学价值与理性价值.此C级要求的试题作为压轴填空题,对学生知识掌握能力和灵活解题能力要求高,解答的整体计算量大、运算较繁;合情合理的难度与区分度,利于高校选拔优秀人才.

二、试题解析

解析一设连结OD交BC于G,则OD⊥BC,所以由于使得D,E,F重合,得到三棱锥,所以即此时三棱锥的高为三棱锥体积令则当x∈时,f′(x)＞0,f(x)单调递增,当时,f′(x)＜0,f(x)单调递减,所以故三棱锥体积的最大值为

图2

图3

三、解读与思考

本问题的解答,考生要基于平面图形几何特点和度量关系,借助空间想象建构翻折平面图形而获得研究对象.在这一从二维平面升维至三维空间的动态变化过程中,考生不仅需要细致感知形变化中数量与位置的变化,而且要能利用代数的方法进行几何的描述抽离出的几何体视图.这一对问题初步识别,是命题者考查数学素养中直观想象的精巧设计;缘于直观想象就是借助于空间想象和数学经验,感知事物的形态与变化,进行代数信息分析、几何特征抽象、图形猜想、数形论证,是对研究的数学对象直接的感知与认识.

经历翻折变换,新生成的几何体“丢失”了平面图形的几何特征,仅呈现三棱锥的视图;这种数学抽象的过程,也是数学建模的过程.数学抽象是数学建模的必经之路,数学模型是舍弃对对象的空间形式和数量关系之外的各种性质,是对研究的对象或者过程进行延伸到只剩下“形式和关系”的极限情况下的理想化,是理想化的数学抽象.这一解决问题阶段,考生要对现实的问题进行抽象,用数学的眼光观察世界、用数学的语言表达问题、用数学的方法建构熟悉的几何体模型,是对数学建模素养进行考查.

而对动态变化三棱锥的数与量的研究,是基于数学推理解决问题的过程,是用数学知识解析世界,发展数学运算的过程.数学运算是前一阶段的逻辑推理分析问题的具体化;是在明确运算对象的基础上,依托代数运算法则解决数学问题的基本手段.清晰的推理是前提,是数学运算的“航道”绘制;而数学运算则是“驰骋江海”,是分析问题的具体化.不难发现,该压轴题对考生核心素养的考查,不单一、不侧重,是一个自然融合的有机整体;是对考生数学基本特征的思维品质与关键能力以及情感、态度与价值观的综合检测.

可见,如果解题教学仅囿于教师展示解法、就题论题,让学生课堂记住套路、考试回忆解答,没有从根本上培养发现问题、提出问题、分析问题和解决问题的能力;就是无效的解题教学.在解题教学中,要引导学生经历“析、译、拓”,践行审题能力、代数翻译与延伸拓展的培养;要挖掘问题中深层的核心素养,在“润物无声”中展示数学核心素养的落实的可行;要提炼素养交融的特点,进而培养学生理性的思维能力与创新意识.