我国债券资产的压力测试

2018-10-16熊熊，兰云

经济研究导刊 2018年27期

熊熊，兰云

（天津大学管理与经济学部，天津300072）

自20世纪70年代布雷顿森林体系崩溃以来，金融自由化和全球化迅速发展，金融体系面临的风险日趋增加，金融危机的发生也越来越频繁。具体来说，20世纪70年代末，拉美债务危机爆发，引发西方国家银行倒闭风潮；20世纪80年代后期美国平均两天内就会有一家银行倒闭；20世纪90年代，从日本经济陷入低迷到墨西哥金融危机、俄罗斯金融危机、亚洲金融危机和阿根廷金融危机等相继爆发，这都显示出金融体系风险的常态化。而2007美国爆发的次贷危机不仅颠覆了美国本土的金融格局，也殃及了大量北欧国家，使曾经的“北欧天堂”不复存在。在2009年，全球经济呈现复苏的萌芽时，希腊、迪拜又相继爆发主权债务危机。种种事实说明，金融风险已呈现常态化趋势，因此风险管理显得尤为重要。

谈及金融风险管理，传统的VaR模型假定风险因子服从正态分布或对数正态分布，风险因子收益的变化具有“平稳”的特征，排除了发生跳跃和其他极端情况的可能性，进而度量在一定置信水平和一定持有期内，某一金融工具或其组合在未来资产价格波动下所面临的最大损失额。因此，VaR模型适用于一个“正态市场”，或者说是正常市场环境，而当金融市场激烈动荡的时候，VaR模型就无能为力了，这也在2007年的次贷危机中得到了证实。

此外，从我国金融市场的情况来看，压力测试出现在我国的金融舞台最早可以追溯到中国银监会为了响应IMF和世界银行于1999年5月联合推出的“金融部门评估规划（FSAP）”，并于2003年9月开始组织对各商业银行的评估工作。此外，中国银监会于2007年制定了《商业银行压力测试指引》旨在提高商业银行的风险管理能力，该指引于2014年进一步修正。除此之外，压力测试在其他领域应用并不广泛，实践并不充分。随着2015年我国加入世界贸易组织的保护期届满，面临的全球金融风险更加严峻，各种无法用VaR模型解决的问题将会无法避免。因此，对我国金融市场尤其是债券市场进行压力测试是十分有必要的。

Dunbar和Irving（1998）指出压力测试主要有三种分析方法：历史情景分析法、结构化情景分析法和根据机构本身特性的情景分析法[1]。BIS（2000）则认为，可分为敏感性分析法、历史情景分析法、虚拟情景分析法、最大损失分析法与极值理论分析法等[2]。Kupeic（2002）依据传统VaR模型的架构，以Delta正态法为基础进行压力测试，将VaR与压力测试构建在同一分析架构中，但其分析架构在理论上忽略了多数资产收益率的实际分布常具有厚尾现象的特性[3]。Embrechts、Mon eil（1997）等一些研究极值理论在风险管理应用的学者，也陆续推导出了可以同时估计出压力情景下的资产组合损失及其发生概率的方法[4]。国外就压力测试的定量方法可分为两类：一类是事先假定分布的方法，包括利用模型估计分布的变异数；另一类是利用蒙特卡罗模拟的方法。

就压力测试的具体操作程序而言，一套完整的压力测试往往包括风险因素识别、情景构建、场景分析和模型选取。Pesaran、Schuermann、Treutler和Weiner（2006）最早采用了VAR模型生成概率情景来对银行系统进行压力测试，并采用冲击响应函数来探究宏观经济变量的冲击[5]。Thomas Breue（r2009）提出采用风险因子的马氏距离来界定压力情景发生的概率。这种方法的优势是可以让决策者在极端情景的可能性和严峻性之间做权衡[6]。在模型选取方面，比较有亮点的是Van den End、Hoeberichts、Tabbae（2006）在奥地利的 SRM 多元 t-copula的基础上提出了另一种新的方法。该方法考虑了宏观经济变量同时变化的情况和他们之间的互相作用，解决了压力测试不能很好地解决相关性的问题[7]。Ricardo Schechtman等（2012）对巴西银行系统的房地产贷款进行压力测试，在Wilson模型基础上加入了分位数回归，有利于估计资产规模的厚尾特征[8]。此外，Vazquez et a1（．2012）首次尝试开拓了新的研究方法，采用VaR模型对风险因子进行建模并识别变量间关系。

相较于国外的研究，国内对压力测试的研究起步较晚。尤其是在2007年以前，大多数学者如郭春松（2005）、黄（2004）、杨鹏（2005）、董天新和杜亚斌（2005）、陈德胜和姚伟峰及冯宗宪（2004）、蒋祥林和王春峰（2005）等先后围绕压力测试的必要性、目的作用、所用方法、国内外的具体实践进行了理论上的探讨[9～14]。在实证方面，以汪寿阳、张静（2002）的研究比较有代表性，他们利用压力测试的方法分析日元贬值对我国2002年出口造成的影响[15]。在2007年以后，学者们更多地围绕压力测试的具体操作程序展开研究，而且结合商业银行信用风险的研究占了大部分。其中，唐文江等（2009）对压力测试情景设置进行了探讨，分析了情景设置的方法，并对情景设置中如何建立宏观经济因子之间的联系、风险因子的传导机制以及情景设置如何与风险管理文化结合、应对突发事件等问题进行了探讨[16]。巴曙松、朱元倩（2010）总结了国际上对压力测试的实践规范与方法，着力研究了事件冲击到承压变量之间的传导机制和缺乏数据情况下的宏观压力测试[17]。徐明东、刘晓星（2008）深入研究了宏观压力测试的理论模型和执行宏观压力测试的主要步骤、方法，并对宏观压力测试的主要难题如银行之间的相互影响与反馈效应等进行了研究[18]。同时，他们也对目前主要的宏观压力测试系统，包括FSAP系统、奥地利央行的SRM系统以及英格兰银行的TD系统，进行了比较研究。杨晓奇（2010）选取不良贷款率为指标评估银行体系稳定性[19]，在Wilson（1997）的研究框架下，使用蒙特卡洛模拟和误差校正模型进行宏观压力测试，评估银行体系在GDP增长率为7%、6%和5%的情景下银行体系的稳定性。

早期的压力测试主要集中在压力测试的执行框架、操作流程上，近期的压力测试则从情景的设置、模型的选取、压力测试的执行、影响测度等多个角度出发，对压力测试进行了较为深入的研究。目前的研究呈现以下几个特征：首先，对宏观经济体系的压力测试研究主要由监管部门领导，对其重点关注的问题是如何兼顾压力情景的严峻性和概率特征，有很多研究对这些问题进行探讨，可惜效果不尽如人意。

一、理论基础

（一）压力测试

压力测试这一概念最早由国际证券事务监察委员会组织（IOSCO）于1995年提出，当时被定义为：“假设市场在最不利的情形下，如利率突然急升或股市突然重挫时，对资产组合的影响效果。”而后，1999年这一定义被扩展为：“将资产组合面临的严峻但有可能发生的极端风险加以认定并进行量化。”此外，2000年国际清算银行巴塞尔银行全球金融系统委员会（BIS committee on the global finanical system，BCGFS），将其定义为一种金融机构用以衡量那些潜在但可能发生的异常损失的模型。就我国而言，银监会将压力测试视为：“将整个金融机构或资产组合置于某一特定的主观想象的极端市场情况，对该金融机构或资产组合在这些关键市场变量突变的压力下的表现状况进行测试，看其是否能经受得起这种市场的突变。”综合国内外对压力测试的定义，本文将压力测试理解成一种衡量在极端市场情况下所导致的潜在损失的方法。

作为金融风险管理的方法之一，压力测试的主要目的在于评估单个债券基金或是商业银行等金融机构在市场发生严峻性的危机事件时所面临的主要风险以及评估在极端不利条件下金融机构体系的稳健性，也就是通过预设某些宏观经济指标发生剧烈震荡时，对债券市场或是银行体系稳健性的影响。压力测试的方法可以运用在优化并检验经济资本配置是否合理、评估金融机构业务风险大小、测量异常但是有可能发生的极端事件对资产组合的影响以及评估金融机构的风险承受特性。

就压力测试的作用而言，主要分成两个方面。第一，对商业银行、债券基金等金融机构来说，压力测试有助于其更完善地评估其抵御风险的能力，增进对本身风险状况的了解，有利其监测有关风险状况的变化，使它的管理层能够将其现在所承受的风险。此外，针对历史数据“失真”的情况，弥补对主要以历史数据及假设为基础的风险评估方法以评估蒙受损失的大小。第二，针对金融机构的监管当局，运用压力测试的方法可以使其对所监管的金融机构在未来可能承受的风险和所能够承受的风险强度有一个宏观的把握并预测在不利的经营条件下风险发生的可能性，对风险的规避有重要的意义。

从操作方法来看，压力测试大体可以分为两种类型：情景测试和敏感性测试。情景分析会涉及多个因子的变动，测试的过程也相对复杂，主要应用于流动性风险、信用风险以及操作风险以及宏观压力测试。根据选取的情景不同又可以细分为历史情景法和假定情景法两种。敏感性测试主要应用于单个风险因子的变动，常用于市场风险的压力测试。

（二）我国上市公司债

新的《公司法》对公司债券的定义是：“指公司依照法定程序发行、约定在一定期限内还本付息的有价证券。”公司债券是公司外部融资的一种重要手段，是企业融资的重要来源，同时也是金融市场上的重要金融工具之一。作为私人公司或公众公司举借债务时使用的工具，公司债由发行人根据发行契约发行，为债券持有人的债权凭证，由发行人承担还本付息的义务。公司债期限可短至几天或长达百年，发行人在债券契约中必须说明资金用途、财务状况。另外，公司债还具有不免税、有固定发行面值、在交易所上市等特征。此外，公司债券的发行通常由评信机构给予信用评定。目前，我国上市流通的公司债评级分为 AAA、AA+、AA、AA-、A+和 A 六类。

二、公司债的压力测试

（一）数据来源及处理

本文对公司债的压力测试采取敏感性测试的方法，对市场风险进行管理，即研究市场利率大幅变动对公司债价格的影响。本文采用公司债的到期收益率代表价格。由于目前我国上市的公司债有 AAA、AA+、AA、AA-、A+和 A 六种评级，只选取单一种类不具有代表性。此外，公司债的期限往往不等，期限也会对收益率造成影响。所以，为了兼顾研究的全面性与效率性，本文选取AAA、AA和A+三类公司债的数据，并将每种类别的3年、5年、7年的收益率进行平均，得到债券到期收益率（ytm）数据。数据以日为频率，期限为2014年12月10日至2016年5月5日共342个数据。本文采用隔夜的上海银行间同业拆借利率（shiboro/n）来代表市场利率。与之对应，选取shiboro/n（s）2014年12月10日至2016年5月5日共342个数据。本文中所有数据均来自Wind数据库，本文模型的实现通过经济计量分析软件——Eviews6.0实现。

（二）VaR模型设定

向量自回归模型（VaR模型）是一种非结构化的多方程模型，它不以经济理论为基础，而是让数据本身来确定模型的动态结构，常用于预测相互联系的时间序列系统以及分析随机扰动对变量系统的动态影响。在模型的每一个方程中，内生变量对模型的全部内生变量的滞后值进行回归，从而估计全部内生变量的动态关系，回避了结构化模型的要求。本文通过建立关于公司债收益率（ytm）和市场利率（shibor）的VaR模型，让数据本身来确定模型的动态结构。

VaR模型的表达式如下：

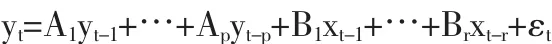
式中，yt是m维内生变量向量，xt为d维外生变量向量，A1…Ap和B1…Br是待估计的参数矩阵，内生变量和外生变量分别由p和r阶滞后期；εt是随机扰动项，同期之间可以相关，但不能有自相关，不能与模型右边的变量相关。

三、基于VaR模型的A+类公司债压力测试实证分析

（一）ADF根检验

单位根检验（Unit Root Test）主要用来判定时间序列的平稳性。如果一个时间序列的均值或协方差函数随时间变化而改变，则这个序列就是不平稳的时间序列。如果该时间序列经过一阶差分后变为平稳序列，则称该序列为一阶单整序列，记作（I1）；如果是经过d次差分后才平稳，则称为d阶单整序列，记作（Id）。在进行VaR模型的估计之前，需要对时间序列进行平整性检验，否则很可能出现“伪回归”的现象，影响结果。

在对时间序列进行单位根检验之前，首先要判断其大体趋势，以便选择合适的ADF模型。

首先，利用Eviews画出两个序列的趋势图。这里对ytm和s序列均采取了对数化处理，不影响后续估计与检验结果。分别命名 log（ytm）和 log（s）为 ytm1和 s1。

图1 ytm1和s1的序列趋势图

由图1可以看到，两个序列含有截距项但并没有明显的趋势，故采取含截距无趋势模型对两个序列分别进行ADF单位根检验。

由表1可以看出，A+级公司债收益率序列和隔夜拆借利率都不是平稳序列，因此不能直接对原序列构建VaR模型。但同时我们可以看到，ytm1和s1的一阶差分序列是平稳的，所以应该对其进行协整检验，以判断是否可以对原序列构建修正的VaR模型。

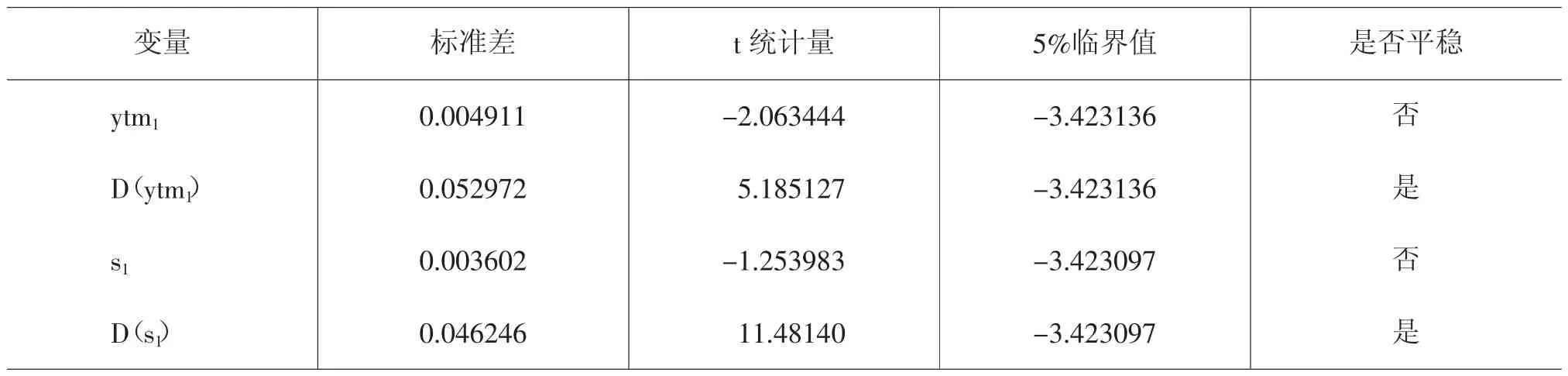
表1 ADF检验结果

（二）协整检验

根据协整理论，如果非平稳变量序列之间的线性组合有不随时间变化的性质或具有平稳性特征，即说明这些非平稳变量之间具有长期稳定的均衡关系。通过前述分析，采用有截距项、但序列没有确定性趋势项的Johansen协整检验方法进行检验。

表2 JJ协整检验输出结果

由JJ检验结果可以看出，变量ytm1和s1之间有1个协整关系存在。

根据检验结果最下方的部分可以得到协整方程（如表3所示）。

表3 协整方程

协整方程为：

log（ytm）=0.08log（s）

s.e.=（0.046）

（三）向量误差修正模型的构建

向量误差修正（VEC）模型是带有协整约束的向量自回归（VaR）模型。只有变量间存在协整关系时才可以构建VEC模型，其多用于具有协整关系的非平稳时间序列建模。由之前的结果，我们可以对ytm1和s1变量序列构建VEC模型。主要从以下几方面进行。

1.最佳滞后期的确定。首先，由根据AIC和SC信息准则确定最佳滞后期。由表4可知，依AIC和SC最小的原则，本模型的滞后期为三期。

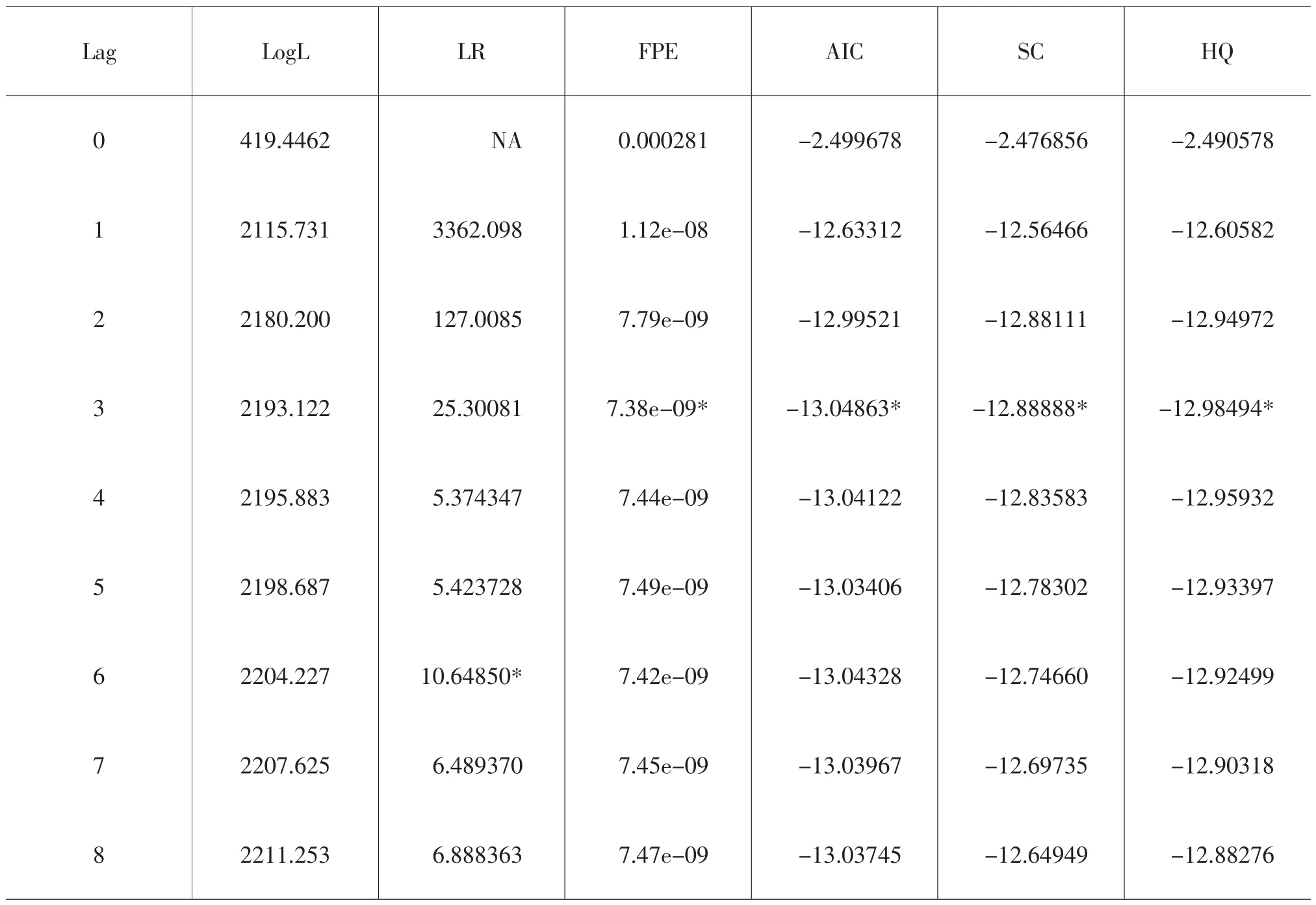
表4 最佳滞后阶数的确定

2.AR根稳定性检验。为了模型的有效性和稳定性，进行 AR特征根的检验，检验结果（如图2所示）。

图2 AR根检验图

根据本文图2可知，该模型的AR根模的倒数均在单位圆内，因此本文建立的VaR模型是稳定的，可以进一步做脉冲响应分析。

3.脉冲响应分析。脉冲响应分析是用来描述一个内生变量对由误差项所带来的冲击的反应，即在随机误差项上施加一个标准差大小的冲击后，对内生变量的当期值和未来值所产生的影响程度。为了研究债券收益率与市场利率之间的动态关系，本文通过脉冲响应分析来看加入市场利率冲击后债券收益率的走势，脉冲响应（如图3所示）。

图3 ytm1和s1各自残差的一个标准偏差冲击的脉冲响应

图6中实线表示受到冲击的变量的走势，虚线范围表示脉冲的正负两个标准误差偏离带。由图可知，当给市场利率一个正向的冲击，收益率会带来同向的冲击，且在5期（日）后影响达到峰值，后来逐渐趋缓。

4.格兰杰（Granger）因果分析。Granger在 1969年提出Granger因果检验法，主要来分析变量之间的因果关系，判断一个变量的变化是否是另一个变量变化的原因。通过Granger因果检验可以判断出变量y能在多大程度上被变量x的过去值所解释，即加入x的滞后期是否提高了解释力度。如果x与y的相关系数在统计上是显著的，则说明“y是xGranger引起的”。如果变量y受到x的滞后期影响，则x与y之间的Granger因果关系成立。本模型的格兰杰检验结果（如表5所示）。

表5 格兰杰因果检验结果

由表5可知，在5%显著水平下，s1能Granger引起变量ytm1，而 ytm1不能 Granger引起变量 s1。

5.A+级债券收益率与shibor的回归结果（见表6）。由表6所示的模型参数估计结果可得到回归方程：

表6 模型回归结果

log（ytm）=-0.003+0.231 log（ytm（-1））+0.185 log（ytm（-2））-0.01log（ytm（-3））-0.017log（s（-1））-0.028log（s（-2））-0.012 log（s（-3））

s.e.=（0.00026）（0.05416）（0.05389）（0.05164）（0.01297）（0.01450）（0.1321）

t=[-1.38868][4.26984][3.44232][-0.19255][-1.32003][-1.95804][-0.93899]

由模型可知，收益率受自身一阶和二阶滞后期正向影响，受市场利率滞后期负向影响。

（四）结论

由协整检验方程结果，对于A+债券而言，当市场利率增加1%。A+级公司债收益率会增加1.083%所以，若出现极端情况，利率上升100个基点，A+级公司债券收益率会上升108.3个基点，即1.083%；利率上升200个基点，A+级公司债券收益率会上升216.6个基点，即2.166%；利率上升400个基点，A+级公司债券收益率会上升433.2个基点，即4.332%。