基于使用与维修数据的飞机使用可靠性研究

蔡复青, 王 戈, 王 悦

(1. 海军航空大学信息融合研究所, 山东 烟台 264000; 2. 中国人民解放军91872部队, 北京 102442;3. 国防科技大学系统工程学院, 湖南 长沙 410073)

0 引 言

可靠性决定产品在规定的条件下,在规定时间内完成规定任务的能力[1]。战斗机可靠性影响其战前可用性和战斗中的任务成功率,因此精确预测其可靠性可以为装备使用和维修保障决策提供科学依据,具有非常重要的实际意义。

目前,可靠性研究工作多在产品研制阶段展开,利用可靠性鉴定、验收、强化等试验中的数据开展可靠性预测,常见方法主要有故障模式和影响分析[2]、故障树分析[3]和寿命分布统计建模[4-5]等。研制阶段可靠性又称固有可靠性,是产品的一种固有属性,由设计、制造过程决定,因此受到产品研制方的广泛关注。但是,相比固有可靠性,产品使用方往往更为关注其使用可靠性。后者是指产品在实际工作过程中表现出的可靠性,除固有可靠性影响因素外,还受到操作使用、维修保障以及工作环境的影响。飞机作为一类重要的武器装备,其使用可靠性是真正影响作战效能发挥的关键因素,因此研究飞机服役期间的使用可靠性预测问题具有十分重要的军事价值和现实意义。

由于飞行任务的多样性及环境的复杂性,飞机可靠性受环境条件影响较大,在不同环境下会表现出不同水平[6]。飞机维修工作主要针对飞机的使用性能,故其可靠性分析的出发点在于确保飞机的使用可靠性在可接受水平之内。当前国内很多有关飞机可靠性的分析工作,只是简单地统计平均故障间隔时间或平均寿命等数值,也是在历史经验的基础上直接套用标准分布。这些做法虽然能得出一些统计规律,但其结果的准确性值得商榷,很难直接应用于维修决策。

目前,国内针对飞机服役期使用可靠性和使用故障率预测的论文或专著可谓寥寥无几。国外虽然在该方面有着丰富经验,但由于涉及核心技术,也较少在公开文献中发表。例如,在波音公司向我国航空公司提供的《Reliability Program for Engineers& Analysts》[7]一书中,仅提供了可靠性分析管理工作的流程和大致思路,在具体的分析方法方面却语焉不详,因而建立一套成熟的可靠性分析与管理系统具有一定的现实意义。

针对以上情况,本文通过分析某型飞机训练和故障数据,在协变量独立假设下,建立了基于多元协变量的飞机使用故障率加法风险模型,定量描述了飞机使用故障率与飞机服役时间、飞行时间强度、飞机起落强度等协变量的关系,可用于实战或训练环境下飞机使用可靠性的预测。

1 数据预处理

飞机在服役期间会产生大量使用和维护数据,这类数据对于判断飞机技术状态提供了重要信息。某机场针对飞机使用维护专门开发了数据收集系统,记录了包括故障部件名称、分系统、故障现象及原因分析、维修方式(换件、维修)、维修工时、服役日历时间、累积飞行时间、累积起落次数、飞机号、服役环境、是否有寿件等关键信息。在开展飞机使用可靠性评估之前,首先需要对原始记录数据进行预处理,主要包括:①剔除重复数据。例如,记录中一些部件级故障和分系统级故障其实是同一故障,因此做合并处理。②统一时间起点。系统各条记录是按日历时间展开的,由于不同飞机服役时间起点不同,因此将服役起始时间均平移到坐标原点,方便后续建模分析。③筛选关键参数。通过绘图观察、相关性分析等方法,确定影响飞机使用可靠性的主要参数,如故障发生时间、服役时间、飞行时间、起落次数等,对上述数据进行筛选提取,并在此基础上,定义飞机瞬时故障率、飞行时间强度、起落次数强度等指标。

2 故障分布与飞行强度关联分析

飞机寿命指标有3类[8]:飞行时间寿命、飞机起落寿命和飞行年限寿命。一架飞机以上3类寿命指标中任何一类先达到,便按此标准淘汰飞机。同一型号飞机固有可靠性是由设计决定的,但在服役过程中,各飞机实际可靠性通常会受到飞行强度、维护水平和外界环境等因素影响。下面,分别就上述几种影响因素展开分析。

本文数据来自国内某军用机场,由于不同飞机投入使用的时间、承担的具体任务不同,飞行强度存在较大差异;维护水平由机场人员素质、软硬件设施、经费投入等决定,对于同一个使用单位,可以看出是近似不变的;飞机设计寿命通常可以达到20年,这上述漫长岁月中,同一地区的外界环境(如气温、降水、风速等)也可以看出是近似平稳的。因此,这里飞机的故障分布主要受到飞行强度影响。飞机的飞行时间、起落次数、服役时间是衡量飞行强度的主要参数,故也是影响飞机使用故障率的重要因素。

基于搜集到的飞行数据,将故障分布与飞行强度关联分析,以验证飞行时间强度与起落次数强度对飞机可靠性产生的影响。研究发现飞机故障发生不仅与飞机飞行时间长短有关,更与单位时间内飞行时间长短有关;不仅与起落次数有关,更与单位时间内起落次数有关。这里,定义飞行时间强度和起落次数强度如下:

飞行时间强度为飞机单位时间内飞行小时,等于总飞行时间/时间间隔,单位为小时/天。

T=∑Ti/N

(1)

式中,N为时间间隔;Ti为时间间隔内各次飞行任务的飞行时间。

起落次数强度为飞机单位时间内起落次数,等于总起落次数/时间间隔,单位为次/天。

C=∑Ci/N

(2)

式中,N为时间间隔;Ci为时间间隔内第i次飞行任务的起落次数。

因此,飞行时间强度和起落次数强度是影响飞机可靠性的重要因素。以某飞机为例,图1和图2展示的是某架飞机飞行强度和故障发生点的分布图关联性。

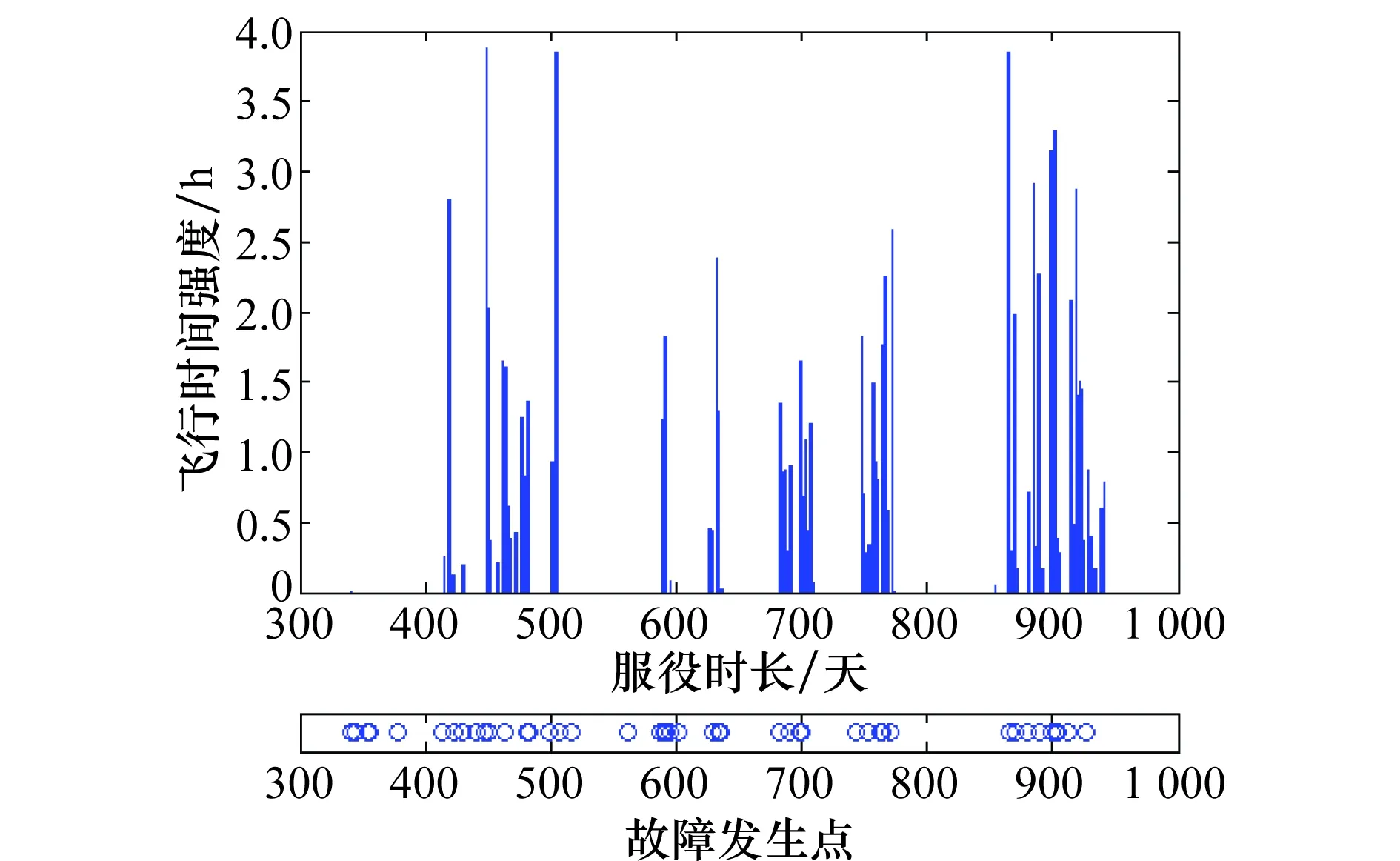
图1 某架飞机飞行时间强度与故障发生点分布图Fig.1 Distribution of flight time strength and failure occurrence time on a certain aircraft

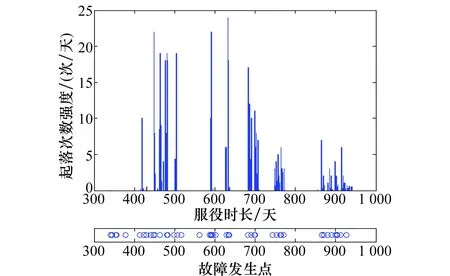
图2 某架飞机起落次数强度与故障发生点分布图Fig.2 Distribution of rise-fall strength and failure occurrence on a certain aircraft

图1和图2中,时间轴上描述的是故障发生点,而折线图描述的是1号飞机两类飞行强度的变化趋势,横轴的都是服役时间。从图1、图2中可以看出,飞行时间强度大的时间段,故障发生情况较密集,由此可以证明飞行强度和故障发生存在高度相关性,说明飞行时间强度和起落次数强度与瞬时故障率存在较强的相关性,飞行时间强度和起落次数强度是影响飞机故障率的重要环境协变量。

3 基于多元协变量使用故障率建模

3.1 多元协变量模型

Cox于20世纪70年代提出比例风险模型[9],比例风险模型既不是参数模型也不是非参数模型,而是一种介于二者之间的模型,是目前对多因素影响下的生存资料分析中最常用的方法。它描述的是环境因素对产品生存函数的影响。比例风险模型是指数模型,将各种因素作为指数项,对失效率的影响会被放大,类似于乘法的思想,因而比例风险模型是乘法模型的变形。在后续的相关研究中,人们更加关注所暴露的风险差异(risk difference),Hsieh提出了适用于体现风险差异的加法风险模型[10]。

由数据预处理结果可知,飞行时间强度大的时间段,出现故障的频率也较高,说明飞行时间强度与故障发生存在较强的相关性,飞行时间强度和起落次数强度是影响飞机使用故障率的重要环境协变量,不同飞行时间强度和起落次数强度下故障发生存在明显差异,即存在风险差异。飞行时间强度反映飞机连续工作时间长短,起落次数强度反映飞机起飞降落频次。理论上,两种飞行强度与各飞机具体任务剖面有关,属于人为可控的主观因素。另一方面,老化时间反映的则是飞机材料、部件随日历时间增加而出现的自然老化现象,属于客观因素。因此,可以近似认为上述三种因素之间近似独立,各自分别作用并影响飞机失效率。基于此,这里采用不考虑各因素之间相关性的加法风险模型,表达式如下：

p(t)=λ0(t)+βT+γC

(3)

其中

λ0(t)=αt

(4)

(5)

(6)

式中，λ0(t)为基础使用故障率;T为飞行时间强度;C为起落次数强度;α,β,γ为模型待估参数。

3.2 模型参数求解

传统的参数求解方法有极大似然估计法、半参数法、非参数法等,而本文构建的使用故障率多元协变量模型将采用数据驱动求解参数的方法,直接利用数据分析的方法进行模型参数估计,使得模型更加适合实际使用情况。数据处理流程如图3所示。第一,对原始记录数据进行预处理,提取起落次数、飞行时间、日历时间、飞机编号、故障数据等建模中需要用到的参数,计算飞机故障率、飞行强时间度、起落次数强度等关键指标;第二,建立故障率的多元协变量预测模型;第三,选取一部分数据量(如80%)用于估计模型参数,剩余数据(如20%)用于模型交叉验证。交叉验证可以检验模型的有效性和预测精度,经验证精度符合要求的模型方可用于失效率预测。这里参数估计采用最小二乘法方法。

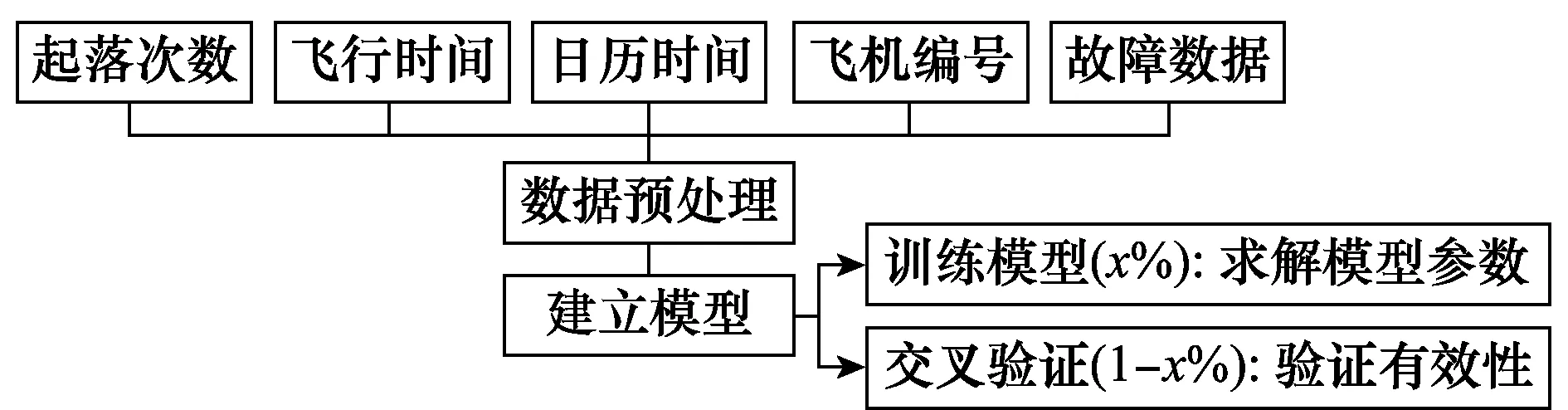
图3 模型参数估计流程Fig.3 Model parameter estimation process

案例中的数据集源自某机场提供的10架某型号飞机记录数据,经过预处理,10架飞机合计有600天数据。取时间间隔为30天,故数据可分为20组,经过计算可得到每组中飞机故障率、飞行时间强度和飞机起落次数强度。由于日历时间、飞行时间强度和起落次数强度单位不一致,会给式(3)中的模型参数估计带来困难。因此,在求解模型之前,我们首先对各参数进行归一化处理,结果如图4所示。本文考虑采用5折交叉验证方法,故将20组数据均分为5份,按前后顺序记为:组1、组2、组3、组4、组5,每次取4份数据估计模型参数,1份数据计算模型预测误差。

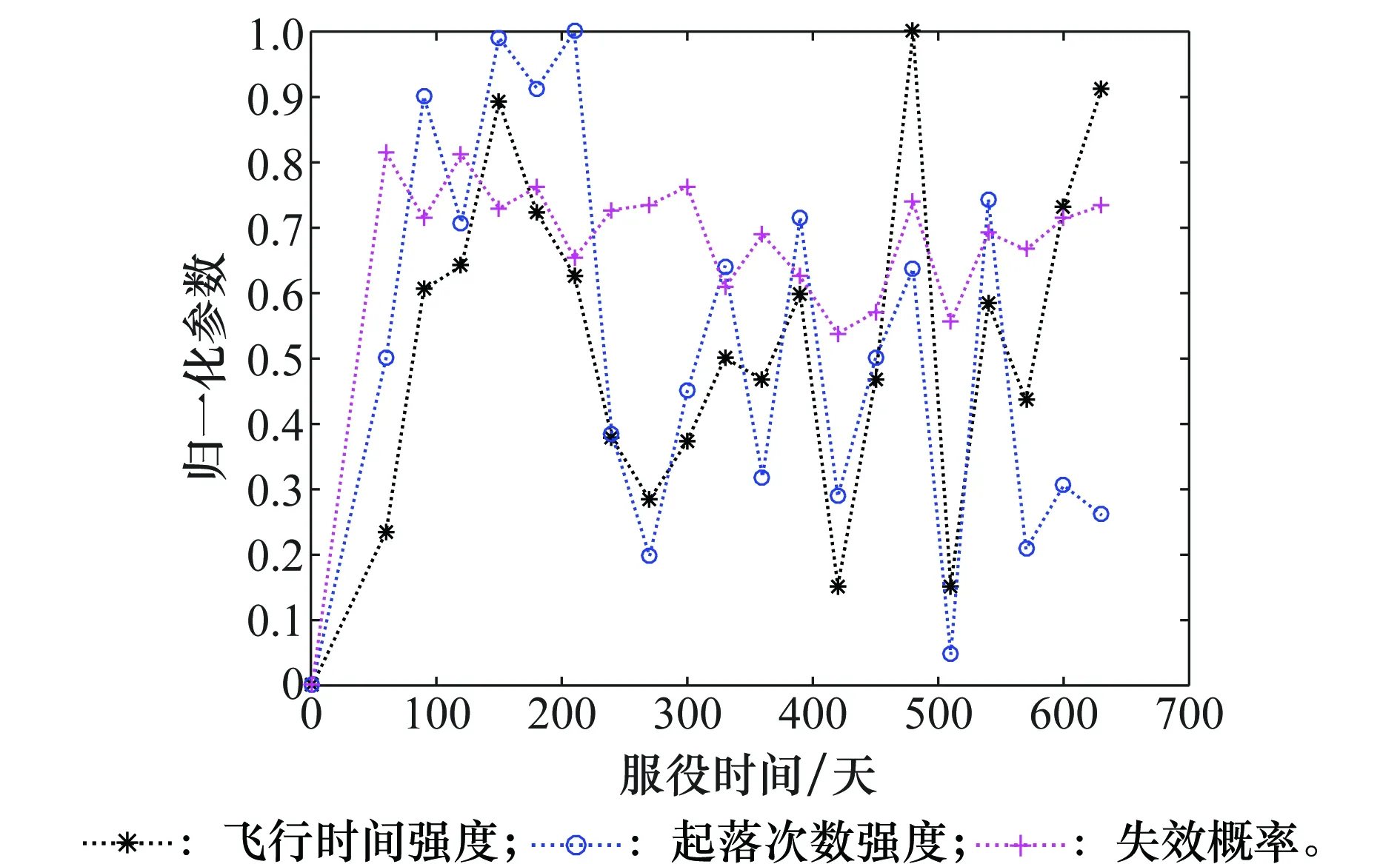
图4 飞机数据预处理图Fig.4 Preprocessing of aircraft data

第1次将组1～组4数据代入模型求解得到模型各参数,第2次将组1～组3、组5数据代入、第3次将组1～组2、组4～组5数据代入、第4次将组1、组3～组5数据代入、第5次将组2～组5数据代入,各组分别求解得到的模型参数如表1所示。

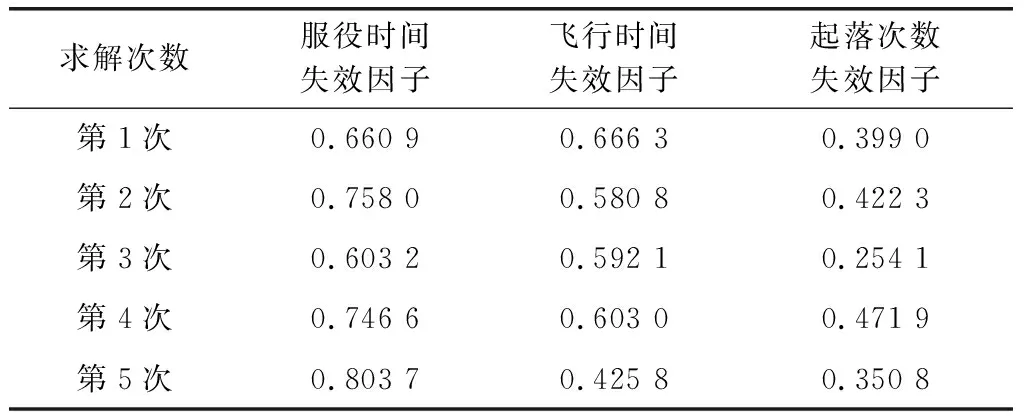
表1 第一组数据求解的模型参数

3.3 模型检验

V折交叉验证在实际应用中是一种被人们普遍使用的模型验证方法,在V>n时,V折交叉验证仅需训练V次,可以大大减小计算复杂度。V折交叉验证[11]方法首先是把数据集平均分为V份,每次从V份数据集中拿出一份数据集作为验证集,剩下V-1的—份数据集作为训练集,重复进行V次,最后平均V次的结果作为最后泛化误差的估计。本文采用5折交叉检验,将5次平均结果作为泛化误差的估计。

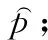
(7)

同理,第2次验证,代入组2相关数据,得到MAE为0.091 7;第3次验证带入组3相关数据,得到MAE为0.127 7;第4次验证带入组4相关数据,得到MAE为0.062;第5次验证带入组5相关数据,得到MAE为0.093 1。

图5展示了上述5折交叉验证误差分析,横轴为验证次数,纵轴为每次验证所对应的误差。

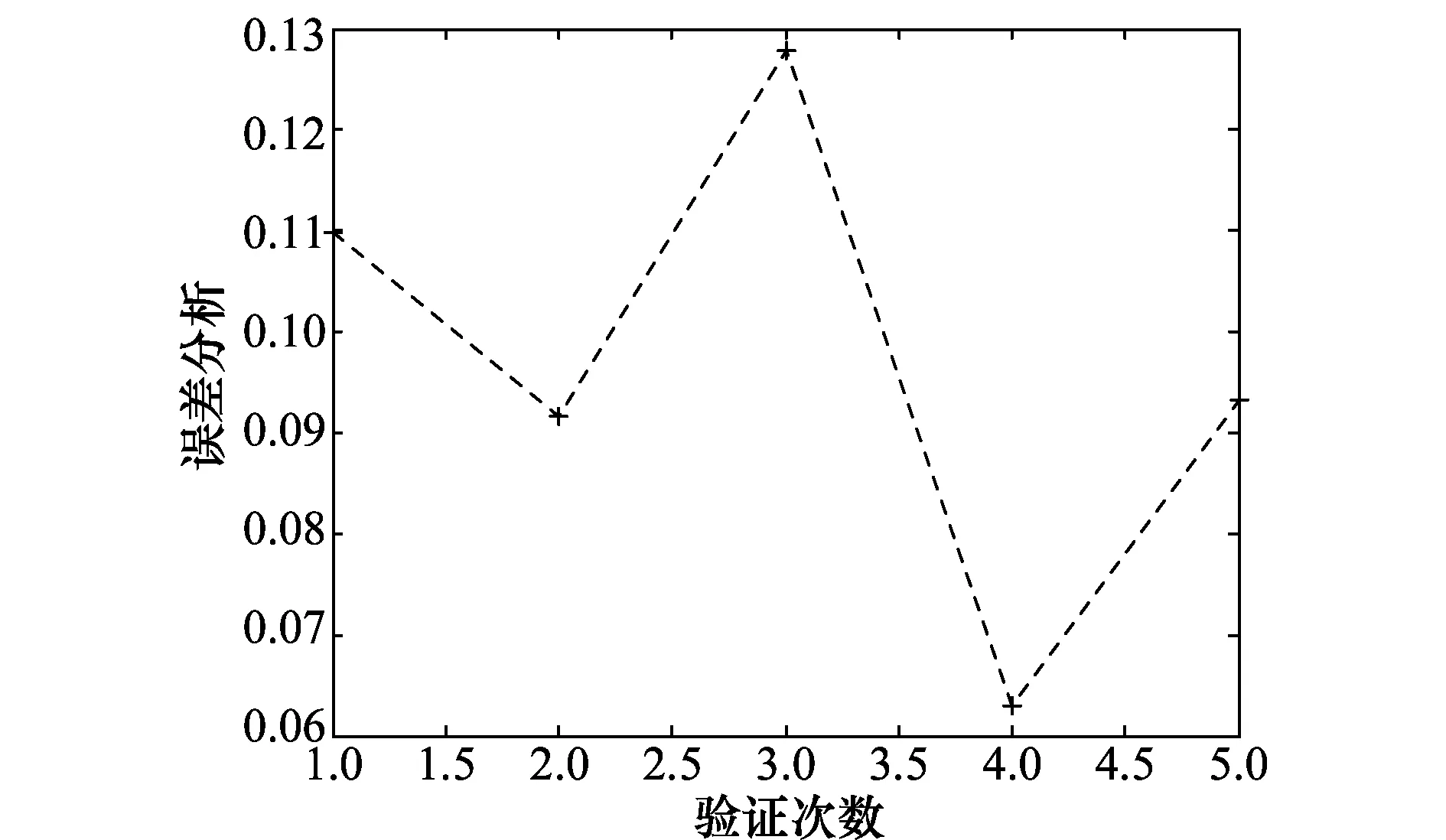
图5 飞机整机使用故障率模型交叉验证分析图Fig.5 Cross-validation analysis of the failure-rate model

经过上述5次验证,将所有的样本作为训练集和测试集,每个样本都对所建立的模型进行了一次验证,其中最大误差为0.127 7,最小误差为0.062 9,平均误差为0.097 0。Pmax=0.863 0,模型相对误差为

0.097 0/0.863 0×100%=11.24%

模型误差较小,从而验证了该模型对于飞机整机使用故障率预测效果较好。

4 飞机使用故障率预测

现将上述5组故障数据代入模型,求解飞机使用故障率加法风险模型参数如表2所示。

表2 飞机使用故障率模型参数

故飞机使用故障率模型为

P(t)=0.595 2·t+0.279 3·T(t)+0.054 9·C(t)

(8)

式中,T(t)为时间t时飞行时间强度;C(t)为时间t时起落次数强度。

这里,影响飞机使用故障率的因素除了飞行时间、起落其次、日历时间外,还包括一些其他因素,如环境因素、人为因素(飞行员技术)等。本文分析时,暂不考虑其他因素的影响。图6是飞机整机使用故障率预测结果图,包括是使用故障率实际值和估计值。结果表明,失效率估计值与真实值较为接近,预测精度可以得到保障。不过,两者之间仍然存在一定误差,预测值较真实值普遍偏高,这可能与建模时忽略了其他影响因素有关。总体而言,该模型可以根据日历时间、飞行强度等参数对飞机失效率进行较高精度预测,有助于帮助机场工作人员制定科学的维修保障方案,并合理规划各架次飞机的日常飞行任务。

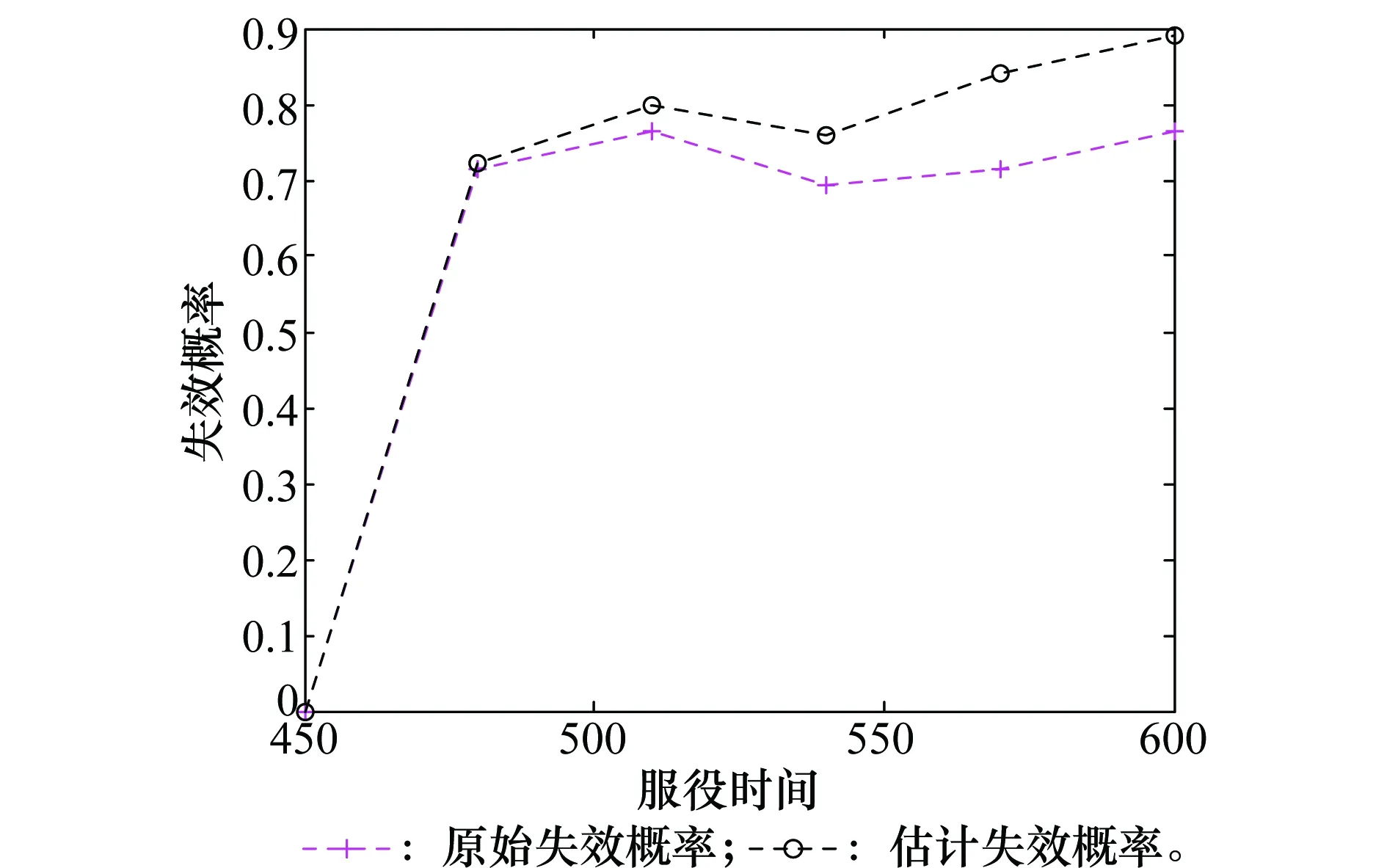
图6 飞机整机使用故障率估计结果图Fig.6 Failure-rate prediction of the whole aircraft

值得注意的是,本文在分析故障时,未对故障具体出现的部位做进一步划分,因此这里的故障率预测结果是针对飞机整机而言的。事实上,飞机按照其功能可以划分为综合航电系统、发动机系统、弹射座椅系统、电气系统、飞行参数系统、军械系统等诸多系统。根据维修记录,可以将故障定位到各系统中,进而根据本文方法对各分系统分别做故障率预测,这里不再赘述。

5 结 论

本文针对基于飞机使用与维修数据的飞机可靠性评估技术开展了相关研究,引入两类飞行强度作为环境协变量,以飞机整机使用故障率模型为依据,建立了飞机使用可靠度模型,描述了飞机使用可靠性随飞行强度和服役年限的变化,以期能将研究成果与我军飞机使用实际情况相结合,建立一套积极有效的飞机使用可靠性评估流程,提高飞机战备完好性。但实际情况中,在完善数据搜集系统的基础上引入其他影响飞机使用可靠性的因素将对大大提高飞机使用可靠性模型的精度。飞机在不同服役环境下,如海岛、沿海、内陆等,飞机会体现不同的使用可靠性;飞行员不同的操作水平对使用可靠性有一定影响;各单位不同的保障维修水平也会影响飞机使用可靠性。但是，由于目前所分析的数据库中没有这些方面信息的记录,因而无法展开相应研究。另外由于分系统内部各部件、附件种类繁多,如果在分系统数据量足够的情况下,可以选取某一分系统进行更加细致的备件需求预测,建立需求预测模型,将其细化到对分系统内各部件、附件的需求量预测,结果将更具有实际指导意义。