利用先验正态分布的贝叶斯网络参数学习

柴慧敏, 赵昀瑶, 方 敏

(西安电子科技大学计算机学院, 陕西 西安 710071)

0 引 言

贝叶斯网络(Bayesian networks, BNs)是将概率理论和图论相结合的不确定性知识推理网络,对非精确知识表达方面具有较强的能力[1-2]。BNs可应用于一些复杂系统的建模,如已成功地应用于故障诊断[3-4]、图像处理[5-6]、网络安全[7-8]、态势预测[9-10]等领域。

一个BNs由两部分构成:一是BNs结构,为有向非循环图,表示了节点(变量)之间的依赖和独立关系;二是网络参数,为各个节点条件概率参数的集合,是对节点间依赖关系的定量表示。在网络结构确定的情况下,如何确定正确的网络参数,即网络参数学习,是BNs应用过程中的重要问题之一。

在一些实际的应用中,如:故障诊断系统、战场态势评估中,样本数据很难获得,可能仅得到样本量小或者数据不完整的样本集。对于这样的问题,一些研究人员提出在进行参数学习时,融入专家针对参数的先验知识,以提高参数学习精度。这一过程也可视为在参数学习过程中加入约束条件[11]。

目前,针对参数的范围约束、单调性约束等讨论得较多,主要的解决方法有:文献[12-14]提出通过建立基于凸约束的目标优化模型进行求解;文献[15]依据约束构建罚项函数,通过降梯度法求解目标函数的最优解,以获得参数值;文献[16-17]利用约束条件和蒙特卡罗抽样方法,获取表示先验Dirichlet分布的超参数,再结合样本数据进行参数估计;文献[18-20]采用引入辅助BNs,完成约束条件下的BNs参数学习;文献[21]将先验约束融入BNs的表示框架中,进行混合BNs的参数学习;文献[22]在具有一定关联关系的样本数据之间添加约束条件,用于不完整数据集下的BNs参数学习。文献[23-24]给出了单调性约束(也称序约束)的解决方法,采用均匀分布来表示序约束,然后采用贝叶斯估计法进行参数估计。

而参数的近似等式约束也是一种较常见的专家先验知识,例如:如果A发生,则B发生的可能性0.8,可得B参数的近似取值的先验知识:P(B=true|A=true)=0.8。针对这一类约束,本文提出采用正态分布对该类约束进行表示,得到先验正态分布;然后通过目标优化获取先验Dirichlet分布的超参数,采用贝叶斯最大后验概率(maximum a posteriori,MAP)估计方法计算网络参数值。

1 贝叶斯网络参数约束分类

对于BNs参数的学习过程中,可以得到一些定性的先验知识,这些定性的先验知识主要可以描述为2种约束形式:线性不等式约束和近似等式约束。

定义1线性不等式约束

对于类似式(1)的专家先验知识:

(1)

式中,Pk,Pk′为不同的网络参数,可以是同一节点的参数,也可以是来自不同节点的参数;c属于[0,1]区间,t为实数,且二者均为常数。可以表示为

(2)

式中,t0,tk均为实数。则式(2)为线性不等式约束。文献[23-24]中的序约束,及参数的范围约束实质上就可以归为线性不等式约束。

定义2近似等式约束

领域专家可以给出类似这样的断言:某个网络参数与另外一个参数近似相等;某个网络参数是另外一个参数近似t倍;某个参数近似等于某个值等,可以表示为

(3)

但具体应用中,式(3)并不方便计算利用,则可采用式(4)的约束描述,即

(4)

式中,ε∈[0,1]。

2 先验正态分布的BNs参数学习方法

2.1 近似等式约束的正态分布表示

对于式(4)的近似等式约束,假定参数Pk′先确定,ε取值较小,则可以将Pk限制在一个较小的范围内,Pk可以取这个范围的任意值。进一步分析式(3)的专家先验知识,可以看出,Pk取值Pk′,或者tPk′,或者c的可能性应该是最大的。

因此,本文引入正态分布构建近似等式约束的数学模型,如图1所示。

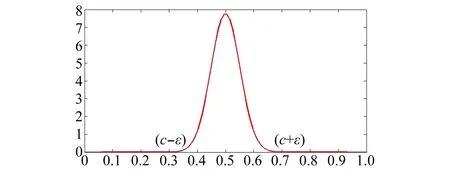
图1 近似等式的正态分布表示Fig.1 Normal distribution representation for approximate equality constraint

图1以近似等式约束|Pk-c|<ε为例,假定c=0.5,ε=0.2。可以看出,Pk取值为c的概率最大,而在c两侧的取值的概率将逐渐减小,符合近似等式约束的特点。则图1中参数Pk的近似等式约束的正态分布为

(5)

式中,μk=c,为正态分布的期望;δ为均方差。本文设定ε=0.2,且需要满足Pk的取值落在区间:[μi-0.2,μi+0.2],则可令式(5)满足:

P(μk-0.2≤Pk≤μk+0.2)=

(6)

由式(6)计算可得:δ=0.051 3。

由此,对式(4)的近似等式约束构建正态分布模型时,依据式(5)将期望设定为:Pk′,或者tPk′,或者c,而均方差为:δ=0.051 3。

2.2 基于贝叶斯MAP的参数估计

贝叶斯MAP参数估计视参数为随机变量,将参数的后验分布的最大值,作为该参数的估计值。现假定BNs由n个节点构成:X={X1,X2,…,Xn},节点Xi存在ri个状态值,假定取值1,2,…,ri。其父节点Pa(Xi)的取值共有qi个组合,假定取值1,2,…,qi。则节点Xi的参数可表示为:θijk=P(Xi=k|Pa(Xi)=j),其中k,j分别表示节点Xi的取值和父节点的组合取值。

在贝叶斯MAP参数估计中,BNs参数的先验分布为Dirichlet分布,其超参数表示为D={aijk}。这样参数的后验概率也将是Dirichlet分布,当参数的后验分布取最大值时,得到该参数的估计值为

(7)

式中,Nijk为样本数据集中满足Xi=k和Pa(Xi)=j的样本的个数。先验Dirichlet分布的超参数可看作参数θijk的虚拟样本数。

可以看出,式(7)中的参数估计值计算需要Dirichlet分布的超参数,而正态分布的参数不能直接用于式(7)中,因此,采用第2.1节中先验正态分布并不适合式(7)中的参数估计。为此,建立目标优化函数,用Dirichlet分布逼近正态分布,获取相应的超参数。

Dirichlet分布的边缘分布为Beta分布,表示为Beta(a,b),则对应到BNs中的每个参数θijk,其相应的先验知识需要服从Beta分布。将正态分布和Beta分布方差的距离最小作为目标函数,期望相等作为约束条件,且要求Beta分布为凸函数,则a>1,b>1为约束条件。则有:

min(DBeta-DG)2

(8)

式中,DBeta,DG分别为Beta分布和正态分布的方差;EBeta,EG分别为相应的数学期望。对式(8)进行求解,可得到Beta分布参数,然后根据式(7)计算θijk的估计值。

3 实验测试

3.1 实验内容

本文测试在完整样本数据集下对本文方法的参数学习精度和运行耗时进行测试,并且与最大似然估计(maximum likelihood estimation, MLE)、无专家先验的贝叶斯MAP估计、约束优化方法(constrained optimization approach, CO)、参照文献[23-24]中的均匀分布表示先验的方法等4种主要方法进行比较,需要说明的是:

(1) 本文方法:实验测试中采用的近似等式约束为式(4)中:|Pk-c|<ε,且ε=0.2,c为相应参数的真实值。

(2) 无专家先验的贝叶斯MAP估计:贝叶斯MAP估计中的先验Dirichlet分布的超参数一般来自专家先验,在无专家先验的情况下,可采用一致先验的方式确定超参数[25],即:式(7)中的超参数aijk=1。本文的实验测试采用的是该种方式。

(3) 约束优化方法:对于约束优化这一类方法,以文献[15]中的约束优化方法为代表进行比较测试。在本文的实验测试中,利用近似等式约束构建罚项函数,且文献[15]所给目标优化函数中的罚项权值设定为1,约束信任度设定为1。在采用降梯度法进行求解时,步长设为1。

实验测试首先采用如图2所示的草坪湿润推理BNs,该BNs被广泛应用于网络推理和参数估计算法的测试中。

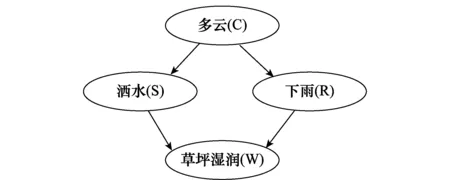
图2 草坪湿润推理贝叶斯网络Fig.2 Structure of lawn wet Bayesian network

该BNs参数的真实值为:根节点C:P(C=true)=0.5,P(C=false)=0.5。其他节点分别为表1所示。

表1 节点S,R和W参数表

在实验测试中,根据图2网络结构和上述所给的参数真实值,采用随机抽样算法生成样本数据。实验测试环境为:操作系统:Windows 7,处理器为:Intel CPU 3.30 GHz,平台软件为:Matlab R2014a。

3.2 测试结果1

(1)参数学习精度测试

本文实验以KL散度为参数学习精度的衡量指标,在不同的数据样本集下进行了测试,测试过程中对图2中的4个节点的参数均加入近似等式约束。测试样本集样本量分别为:10,20,30,50,100,对相同样本量的样本集重复测试10次,分别统计4个节点:C,S,R,W的平均KL散度值,结果如表2所示。

由表2的测试结果可以看出,在参数学习精度方面,本文方法和先验均匀分布方法明显要好于最大似然估计、无专家先验的贝叶斯MAP估计、约束优化方法,尤其是在样本量较小的情况下,如:10样本集和20样本集。但在样本较多,即样本充足的情况下,这5种方法的精度均能达到较好的水平,例如:在100样本集下,4个节点的平均KL散度在5种方法中均没有超过0.060。

单纯分析本文方法和先验均匀分布,在不同的样本集下采用本文方法,节点的平均KL散度多次出现为0.0,出现的次数为:13次,明显多于先验均匀分布出现的次数:5次。因此,本文方法的精度要更好于先验均匀分布方法。

为了从整体上比较这5种方法,将表2中不同的测试样本集和不同的测试方法下,4个节点的平均KL散度值相加,得到图2中的BNs的平均KL散度值,其结果如图3所示。

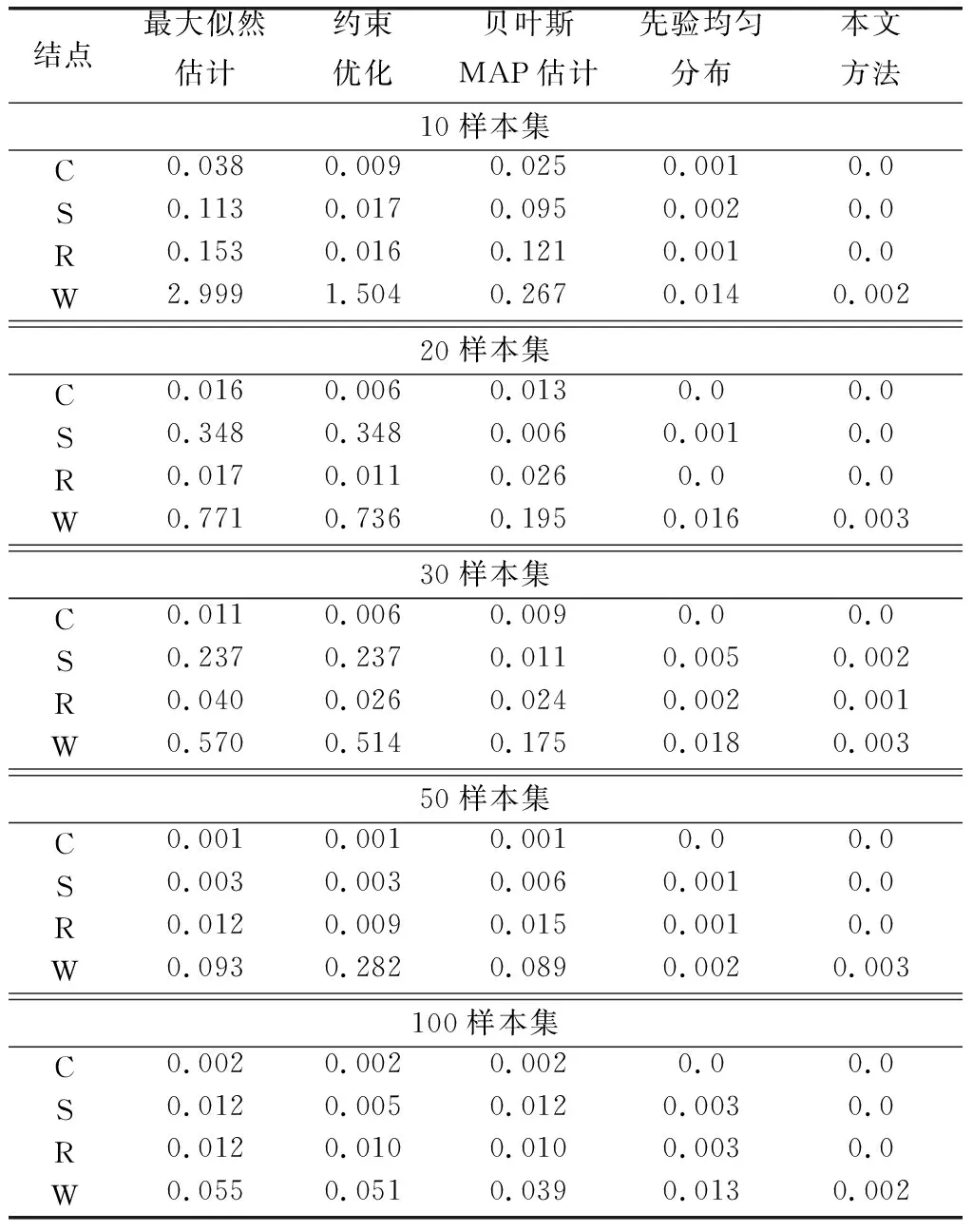
表2 节点C,S,R,W的平均KL散度值

由图3曲线可以看出:在样本量为10、20、30的情况下,本文方法和先验均匀分布的精度高于其他3种方法,无专家先验的贝叶斯MAP估计法的精度高于约束优化方法和最大似然估计方法。在样本量为50、100的情况下,最大似然估计、无专家先验的贝叶斯MAP估计、约束优化方法的精度近似趋于一致,但本文方法和先验均匀分布的精度仍高于其他3种方法。

为了进一步分析本文方法和先验均匀分布方法,将图3中的这2个方法的曲线单独显示,如图4所示。

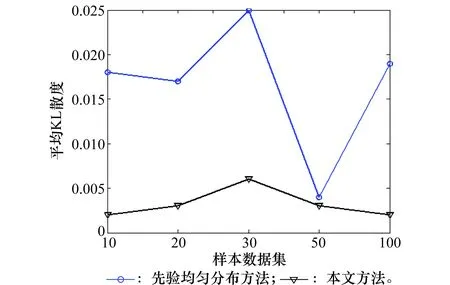
图4 本文方法与先验均匀分布方法的平均KL散度(草坪湿润贝叶斯网络) Fig.4 Average KL divergence for the proposed method and the method of prior uniform distribution(lawn wet Bayesian network)

由图4可以看出,本文方法和先验均匀分布方法均能得到较高的精度,但本文方法在5个样本集下的精度都高于先验均匀分布方法。

(2)运行时间测试

在不同的样本集下,对5种方法的运行时间进行测试,每一种样本集重复测试10次,统计各方法的平均运行时间,测试结果如表3所示。

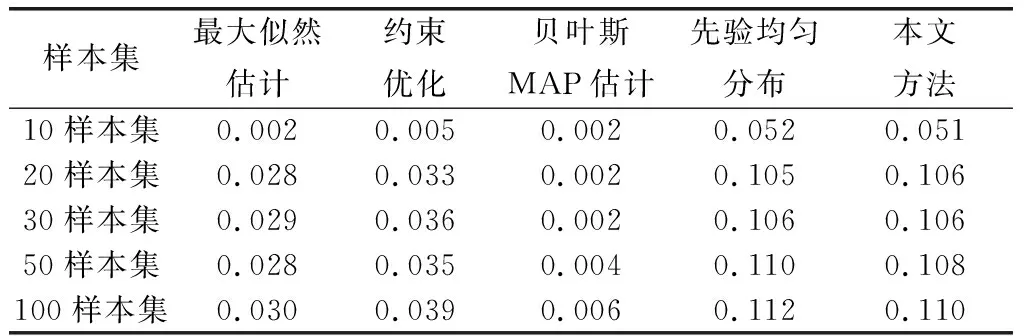
表3 5种方法的运行时间

为了直观显示5种方法的运行时间比较,给出如图5的曲线表示。

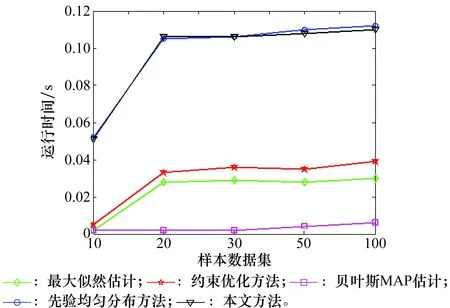
图5 5种方法运行时间比较(草坪湿润BNs)Fig.5 Comparison of run time for five method (lawn wet Bayesian network)

由图5可以看出,本文方法和先验均匀分布方法的运行时间近似相等,且耗时大于其他3种方法。

显然,本文方法提高了参数学习精度,但增加了运行时间。但进一步综合比较学习精度和运行时间的测试结果,本文方法提高学习精度程度要远高于增加运行时间的程度。例如:10样本集下,本文方法相比于约束优化方法,精度提高了700多倍,运行时间增加了近10倍。因此,综合考虑学习精度和运行时间,本文方法优于其他4种方法。

3.3 测试结果2

为了进一步对本文所提出的方法进行实验测试,选择常用的用于测试的BNs:Alarm(www.norsys.com/netlibrary/index.htm),该BNs共有37个节点,最多父节点个数为4个。

参照第3.1节中的测试内容和实验测试环境,对Alarm BNs在数据样本集:50,200,400,600,1 000,以BNs平均KL散度和运行时间为衡量指标,进行实验测试。其中,BNs平均KL散度与第3.2节中的相同,即为:网络各节点的平均KL散度值的总和。

(1) BNs平均KL散度

测试过程中对Alarm BNs的37个节点的参数均加入近似等式约束,且所加入的近似等式约束按照第3.1节中(1)。对相同样本量的样本集重复测试10次,分别统计37个节点的平均KL散度值,并进行相加求和,结果如图6所示。

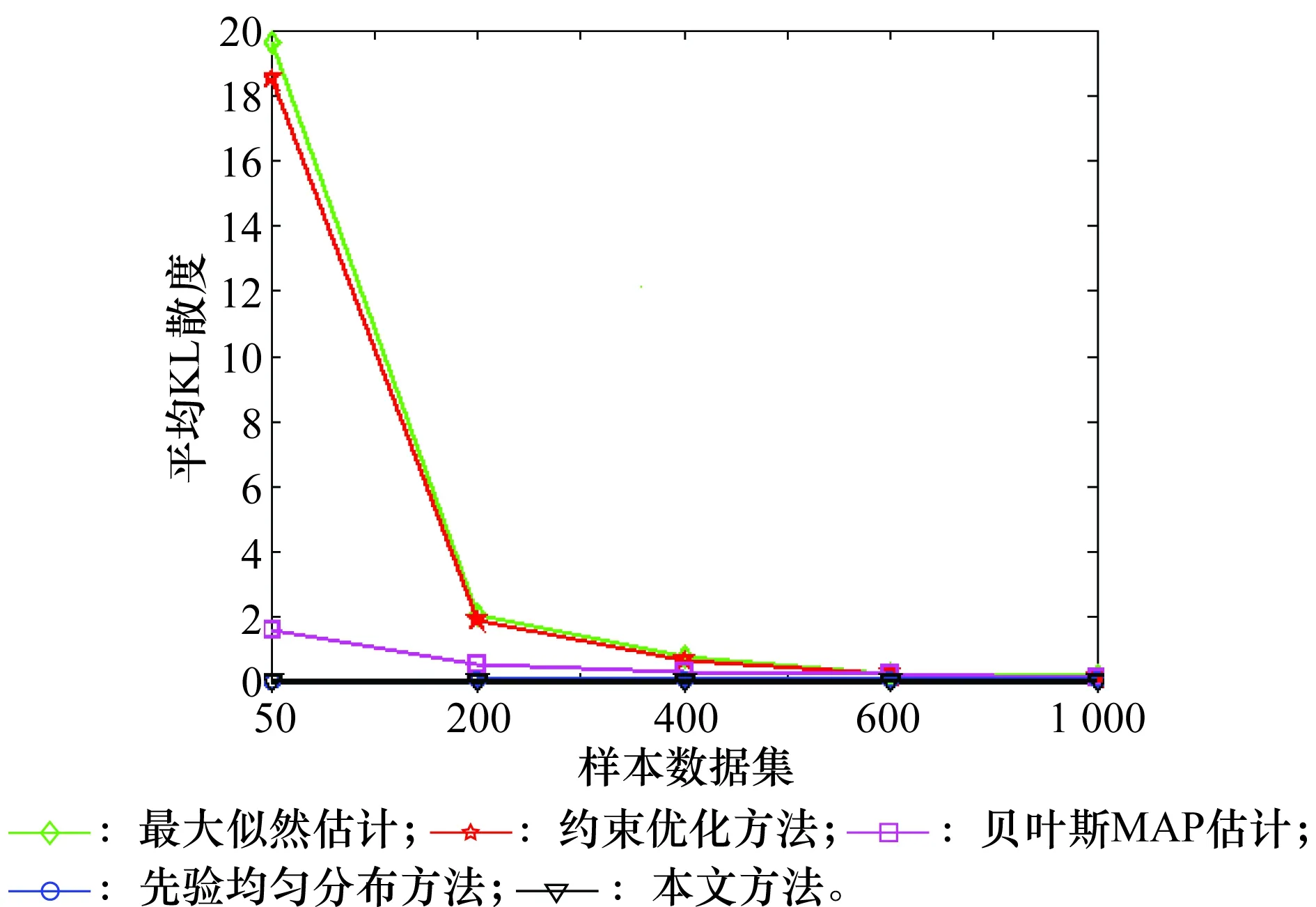
图6 不同样本集下BNs(Alarm)平均KL散度Fig.3 Average KL divergence of Bayesian network (Alarm) under different data set

图6中,在样本集为:50,200,400,本文方法和先验均匀分布方法的平均KL散度值均小于其他3种方法。而在样本集为600,1 000时,5种方法的平均KL散度分别为:最大似然估计:0.266,0.176;约束优化方法:0.259,0.169;贝叶斯MAP估计:0.245,0.163;先验均匀分布方法:0.082,0.071;本文方法:0.017,0.016。本文方法和先验均匀分布方法的平均KL散度均低于其他3种方法,即参数学习精度好于其他3种方法。

为了进一步分析本文方法和先验均匀分布方法,将图6中的这两个方法的曲线单独显示,如图7所示。

由图7可以看出,本文方法在5个样本集下的参数学习精度均好于先验均匀分布方法。

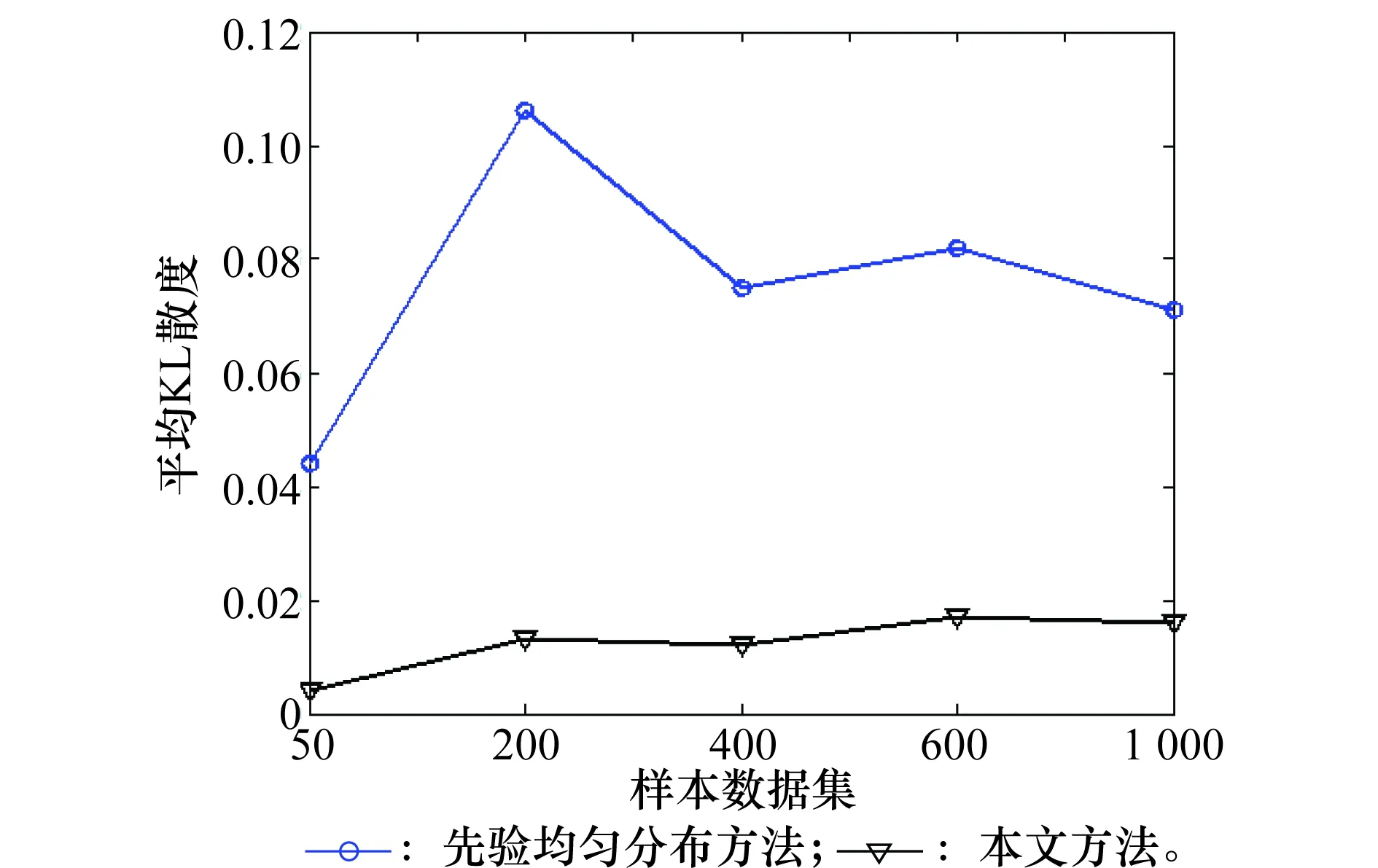
图7 本文方法与先验均匀分布方法的平均KL散度(Alarm BNs)Fig.7 Average KL divergence for the proposed method and the method of prior uniform distribution (Alarm Bayesian network)

(2)运行时间

针对Alarm BNs,在样本集:50,200,400,600,1 000下,对5种方法的运行时间进行测试,重复测试10次,统计各方法的平均运行时间,测试结果如图8所示。

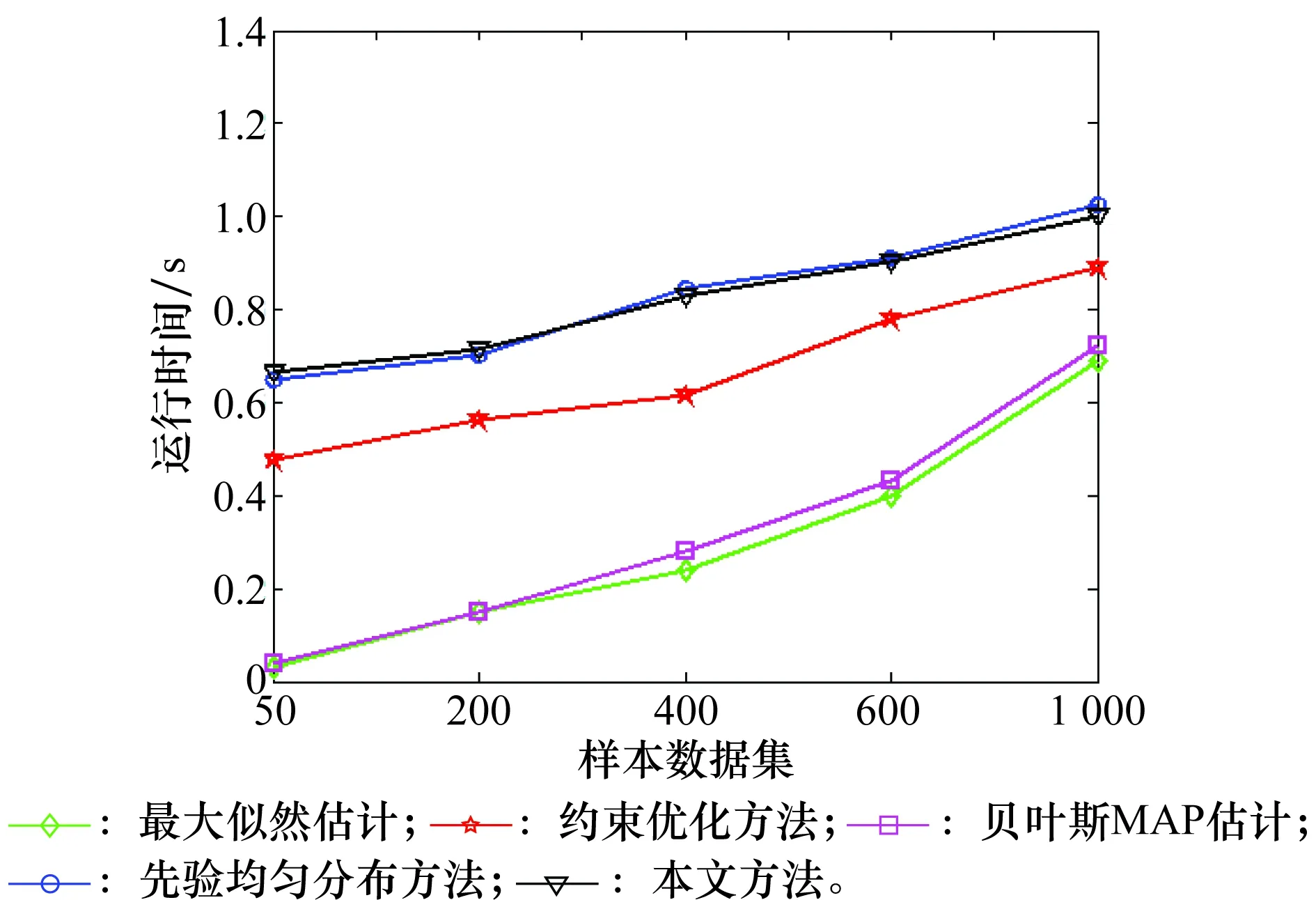
图8 5种方法运行时间比较(Alarm BNs)Fig.8 Comparison of run time for five methods (Alarm wet Bayesian network)

图8中,本文方法和先验均匀分布方法的运行时间近似相等,但都大于其他3种方法。进一步综合比较KL散度和运行时间,在样本集:50, 200的测试中,本文方法相比于其他4种方法,参数学习精度的提高倍数远大于运行时间的增加倍数。

在样本集:600,1 000的测试中,本文方法相比较于其他4种方法学习精度提高的倍数为:最大似然估计:15.65,11.00;约束优化方法:15.24,10.56;贝叶斯MAP估计:14.41,10.18;先验均匀分布方法:4.82,4.44。而运行时间相比于其他4种方法增加的倍数依次为:最大似然估计:2.26,1.45;约束优化方法:1.16,1.12;贝叶斯MAP估计:2.09,1.39;先验均匀分布方法:0.99,0.98。可以看出,本文方法参数学习精度提高的倍数均大于运行时间增加的倍数。因此,综合考虑学习精度和运行时间,本文方法是优于其他4种方法。

4 结 论

本文针对BNs参数的近似等式约束,提出了采用正态分布的先验表示方式,实验测试结果表明:该方法的参数学习精度好于最大似然估计、无专家先验的贝叶斯MAP估计、约束优化方法等4种方法,而运行时间要高于这4种方法。但综合考虑比较KL散度和运行时间,相比较于其他4种方法,本文方法参数学习精度提高的倍数均大于运行时间增加的倍数。本文只是考虑了完整数据样本下的参数学习,后续需要进一步研究缺失数据样本下的学习问题。