单轴旋转SINS方位陀螺漂移精确估计方法

胡 杰, 朱倚娴, 石潇竹

(1. 中国电子科技集团公司第二十八研究所, 江苏 南京 210007;2. 空中交通管理系统与技术国家重点实验室, 江苏 南京 210007;3. 东南大学微惯性仪表与先进导航技术教育部重点实验室, 江苏 南京 210096)

0 引 言

惯性导航系统的北向陀螺漂移和方位陀螺漂移会引起位置的积累性误差,可以通过提高惯性测量单元(inertial measurement unit, IMU)的精度或者采用系统级补偿方法提高定位精度[1-3]。系统级补偿方法具有见效快、实现简单等优点,目前有两种常用方法[4-6]:①采用旋转调制技术消除器件误差影响;②利用Kalman滤波器估计IMU误差并在线补偿。旋转式(strapdown inertial navigation system,SINS)周期性转动IMU抵消了与转轴垂直方向上的器件误差,提高了系统导航精度。国外激光陀螺旋转式SINS已经应用于水面舰船或潜艇,如美国的MK39Mod3C单轴旋转SINS,MK49双轴旋转SINS等[7-9]。国内相关单位也进行了旋转式SINS的研究工作,如国防科学技术大学、哈尔滨工程大学、航天科工33所以及航天科技13所[4, 10-12]等。

单轴旋转SINS的方位陀螺性能,特别是常值漂移和陀螺标度因数误差,决定了导航系统的性能指标,如方位陀螺漂移为0.01 °/h,地理纬度为45°时,24h后其位置误差约为10n mile[13]。为了提高单轴旋转SINS长时间导航精度,许多学者对此进行了研究。孙枫[14]提出倾斜放置旋转轴以尽可能抵消3个转轴方向上的IMU误差,该方法所采用的转位方式实际中难以实现。于旭东[15]提出利用经纬度误差辨识方位陀螺漂移,辨识时间长且需要载体静止不动。陆志东[16]对双轴旋转SINS误差进行了分析,并提出了一种IMU误差系统级标校方法,通过周期性转动IMU能够有效估计出IMU误差。Gao[17]研究了旋转式SINS初始对准与自标校技术,惯导系统启动后进行初始对准的同时对IMU误差进行自校准,根据仿真结果可以看出,方位陀螺漂移无法进行有效估计。孙伟[18]同样研究了双轴旋转式惯导系统IMU在线标定方法,根据实验结果可以看出,初始姿态和航向角精度影响方位陀螺漂移的估计精度。综上文献可知,目前单轴旋转SINS方位陀螺漂移标校方法主要有最小二乘辨识与Kalman滤波估计两种方法,其中基于经纬误差的最小二乘辨识方法耗时长,且需要载体保持静止不动,实际应用并不广泛,而Kalman滤波估计法目前较多的应用在双轴旋转SINS中,因此需要结合单轴旋转SINS误差传播特性,研究一种适用于单轴旋转SINS的方位陀螺漂移估计方法。

本文对惯导系统误差传播规律进行了分析,提出了一种单轴旋转SINS方位陀螺漂移估计方法。首先分析了单轴旋转SINS方位陀螺漂移估计原理,给出了方位陀螺漂移估计流程,然后建立了Kalman滤波模型,给出了一种优化后的Kalman滤波方法。进行了系统验证实验,结果表明该方法具有可行性,能够为中等精度单轴旋转SINS的研制提供参考。

1 单轴旋转误差补偿原理

1.1 坐标系定义及单轴旋转SINS系统构成

单轴旋转SINS中,IMU放置在旋转机构上,可以绕转动轴作往返运动。定义旋转坐标系为s系(oxsyszs),其余坐标系与常规SINS定义一致,分别有载体坐标系(b系,oxbybzb),惯性坐标系(i系,oxiyizi)以及导航坐标系(n系,oxnynzn)[19]。初始时刻旋转系与载体系重合,系统通电后电机驱动IMU以角速度Ω绕转动轴旋转,则当时间为t时其互相之间的转换矩阵为

(1)

图1为单轴旋转SINS结构图,系统主要由旋转机构、IMU以及导航计算机组成。IMU包括3个光纤陀螺和3个石英挠性加速度计。力矩电机能够驱动IMU作正反旋转运动,角度编码器实时给出旋转系相对载体系转过的角度。

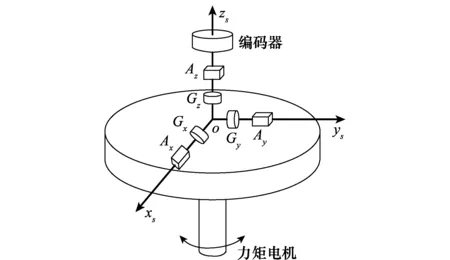
图1 单轴旋转SINS结构图Fig.1 Single-axis rotational SINS structure

1.2 旋转调制原理分析[20-21]

在单轴旋转SINS中,陀螺和加速度计输出值为

(2)

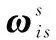
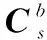
(3)

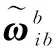
将式(2)代入到式(3)中得:

(4)

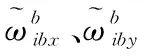
由式(4)知,水平方向上的陀螺漂移和加速度计偏置经过旋转调制后其在一个周期内积分为零,而转轴方向上惯性量漂移无法被抵消,其对导航精度的影响依然存在。

1.3 单轴旋转方案

单轴旋转主要有单向连续旋转、大于360°两位置正反旋转以及小于360°四位置正反旋转3种方案。为了减小IMU标度因数误差与转轴运动耦合而带来的系统级误差,采用正反旋转方案[22]。同时小于360°旋转方式可靠性最高,因此本文采用四位置正反旋转方案,如图2所示。

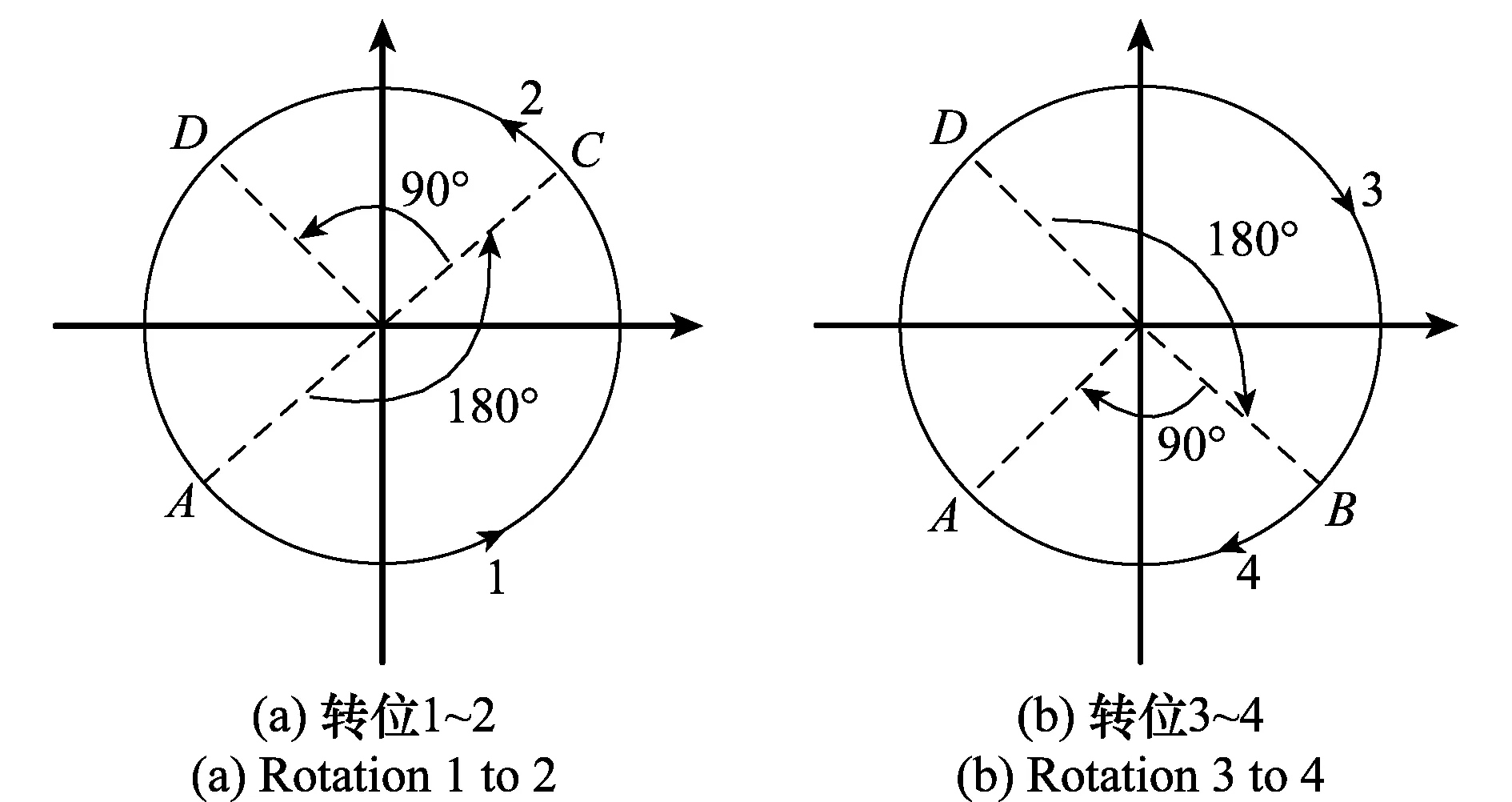
图2 单轴旋转方案Fig.2 Single-axis rotational scheme

转位1IMU由A点逆时针转动180°到达C点,然后停止Ts;

转位2IMU由C点逆时针转动90°到达D点,然后停止Ts;

转位3IMU由D点顺时针转动180°到达B点,然后停止Ts;

转位4IMU由B点顺时针转动90°到达A点,然后停止Ts。

然后按照上述顺序循环运动,且在每个位置处停留时间为5 min。

2 方位陀螺漂移估计原理

单轴旋转SINS方位陀螺漂移可观测性较差,为了减小系统误差对方位陀螺漂移估计精度影响,需要对SINS误差方程进行分析[23-24]。图3为SINS误差传递过程。

图3 SINS误差传播路径Fig.3 Errors propagation path of SINS

图3中,εE、εU为等效东向陀螺漂移和方位陀螺漂移;δvN为SINS北向速度误差;δL为SINS纬度误差;φx、φz分别表示东向失准角和方位失准角。由图3可知,方位陀螺漂移激发方位失准角,而方位失准角会进一步引起东向失准角,同时东向陀螺漂移也会引起对应的东向失准角,可以看出,东向陀螺漂移与方位陀螺漂移具有相同的误差传播路径。因此,当采用“速度匹配”或者“位置匹配”误差方程估计方位陀螺漂移时,对应的东向陀螺漂移、初始方位失准角等都会影响方位陀螺漂移估计精度。

在单轴旋转SINS中,水平方向上的IMU误差已经被调制,因此可以忽略东向陀螺漂移对方位陀螺漂移估计精度影响,方位失准角精度最终决定了方位陀螺漂移估计效果。同时通过SINS旋转式精对准可以得到较为准确的方位角,本文利用该特点设计了一种适用于单轴旋转SINS的方位陀螺漂移估计流程,共3步,如图4所示。

步骤1单轴旋转SINS通电完成自检后首先进行“惯性系抗晃动基座粗对准”[25-26],可以得到SINS初始姿态和航向角,设定时间为T1;

步骤2启动转位机构进行四位置精对准,利用Kalman滤波器估计3个失准角,精对准结束后反馈修正SINS速度、位置以及失准角,设定时间为T2;

步骤3单轴旋转SINS继续进行四位置转停运动,利用Kalman滤波器在线估计IMU误差,设定时间为T3,然后修正SINS速度、位置、失准角和IMU误差,至此SINS启动前误差标校流程结束,切换系统至纯惯性导航工作模式。

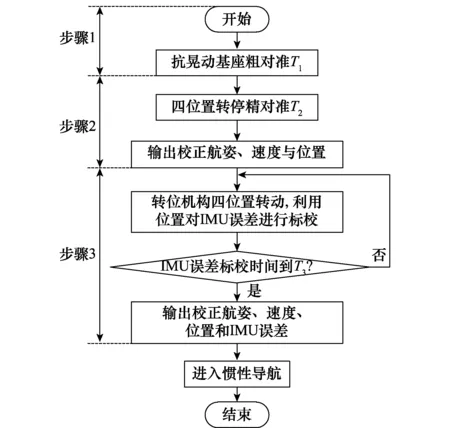
图4 估计流程图Fig.4 Estimation process chart

3 IMU误差估计Kalman滤波模型

3.1 状态方程与量测方程建立

状态向量包括SINS位置和速度误差、3个失准角、陀螺漂移和加速度计偏置以及陀螺标度因数误差,具体可以写成:

(5)

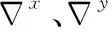
根据捷联惯导系统误差方程建立状态空间模型,可得惯导系统状态方程和量测方程为

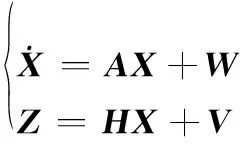
(6)

式中,A为系统状态转移矩阵,可以由SINS误差方程推导得到;W为系统噪声向量;Z为量测向量;H为量测矩阵;V表示系统量测噪声向量。本文利用δL和δλ作为观测量,因此H矩阵可以写成如下形式:

H=[I2×202×13]

(7)

式中,I表示单位矩阵。

式(6)为连续性误差方程,对其进一步离散化可以得到离散化后的状态方程和量测方程:

(8)

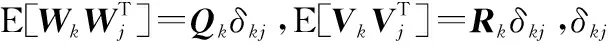
3.2 优化的Kalman滤波方法

在单轴旋转SINS中,由于加速度计尺寸效应、陀螺标度因数误差以及安装误差等因素的存在,IMU转动过程中会引起速度误差(也称为锯齿形速度误差),即Kalman滤波方程中量测新息的突变,从而会带来滤波器较大估计误差。本文对传统Kalman滤波器进行优化,以抑制旋转式惯导系统中锯齿形速度误差引起的滤波发散。

当IMU从一个位置转动到另一个位置的旋转过程中,惯导系统只进行导航解算和Kalman滤波时间更新,而不进行滤波量测更新,以隔离锯齿速度误差对滤波精度影响,当转动完成后,恢复Kalman滤波正常计算,以下为算法具体计算流程。

步骤1时间更新

(9)

(10)

步骤2量测更新

(11)

(12)

Pm,k+1=Pk+1/k-Kk+1Hk+1Pk+1/k

(13)

步骤3综合判断

(14)

Pk+1=β·Pm,k+1+(1-β)·Pk+1/k

(15)

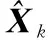
如果转位机构转动则置β=0,此时Kalman滤波器输出值为一步预测值,隔离了锯齿形速度误差对系统精度影响;当转位机构停止转动时β=1,此时利用量测新息值对滤波器状态量进行估计,循环判断直至整个滤波过程结束,转位机构的运动状态可以由角度编码器读取。

4 验证实验

为了对本文所提出的方位陀螺漂移估计方法进行充分验证,利用实验室研制的单轴旋转SINS分别进行了转台摇摆和车载行进间验证实验,单轴旋转SINS的IMU由3个光纤陀螺和3个石英挠性加速度计组成,主要技术参数见表1,系统验证实验中控制IMU做单轴四位置正反转停旋转运动,设计了如下两种实验方案。

表1 单轴旋转SINS技术参数

方案1转台摇摆实验,将单轴旋转SINS放置在三轴模拟转台上,如图5(a)所示,控制转台做三轴摇摆运动,其中航向角摇摆幅度为5°,频率为0.2 Hz,俯仰角摇摆幅度为5°,频率为0.2 Hz,横摇角摇摆幅度为2°,频率为0.8 Hz,然后启动单轴旋转SINS开始进行实验;

方案2车载行进间实验,将单轴旋转SINS放置在跑车实验系统上,如图5(b)所示,车载实验中基准位置由GPS提供,其位置误差小于10 m,车载实验地点为贵阳市内某条道路,如图6所示,图中A点为实验起始点,行驶至B点掉头,然后继续行驶至C点停止,整个实验过程中控制车辆行驶速度为10 km/h。

图5 验证实验环境Fig.5 Verified experiment environment

标定流程中设定时间T1=1 min,T2=15 min,T3=2 h,车载实验标定结束后继续进行12 h的导航验证实验。表2、表3对转台摇摆实验和车载行进间实验进行了统计,图7～图9给出了车载实验过程中IMU误差估计曲线。

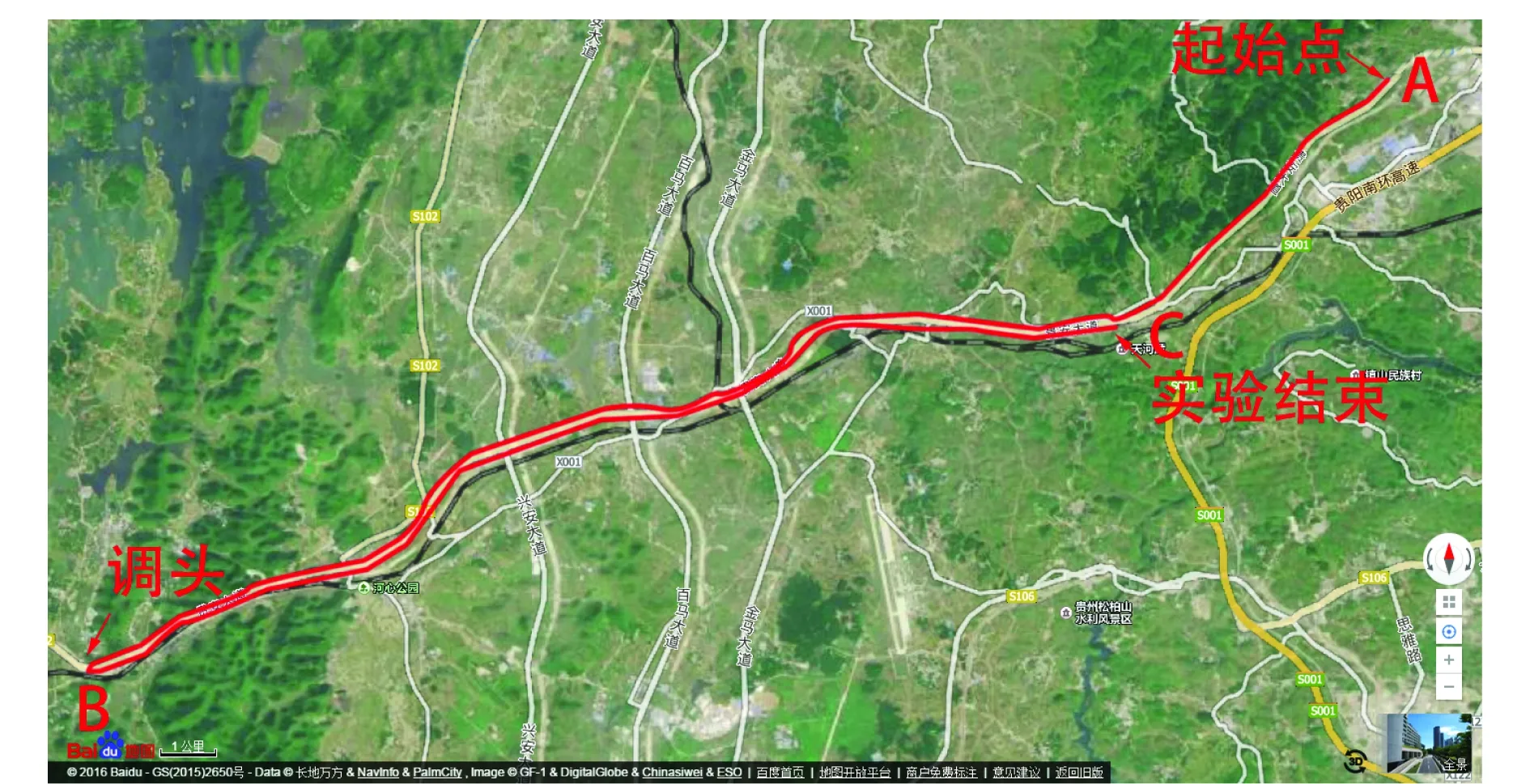
图6 车载实验路线Fig.6 Vehicle experiment route

参数Δx/μgΔy/μgεx/((°)/h)εy/((°)/h)εz/((°)/h)摇摆69.02-32.750.006 9-0.003 10.009 1车载75.63-28.620.007 4-0.002 90.008 8

表3 陀螺标度因数误差估计值

由表2和表3可看出,摇摆与车载两种实验环境下,IMU误差估计值相当,同时该估计值与本实验所使用的IMU精度相当,说明本文所给出的方法具有可行性。

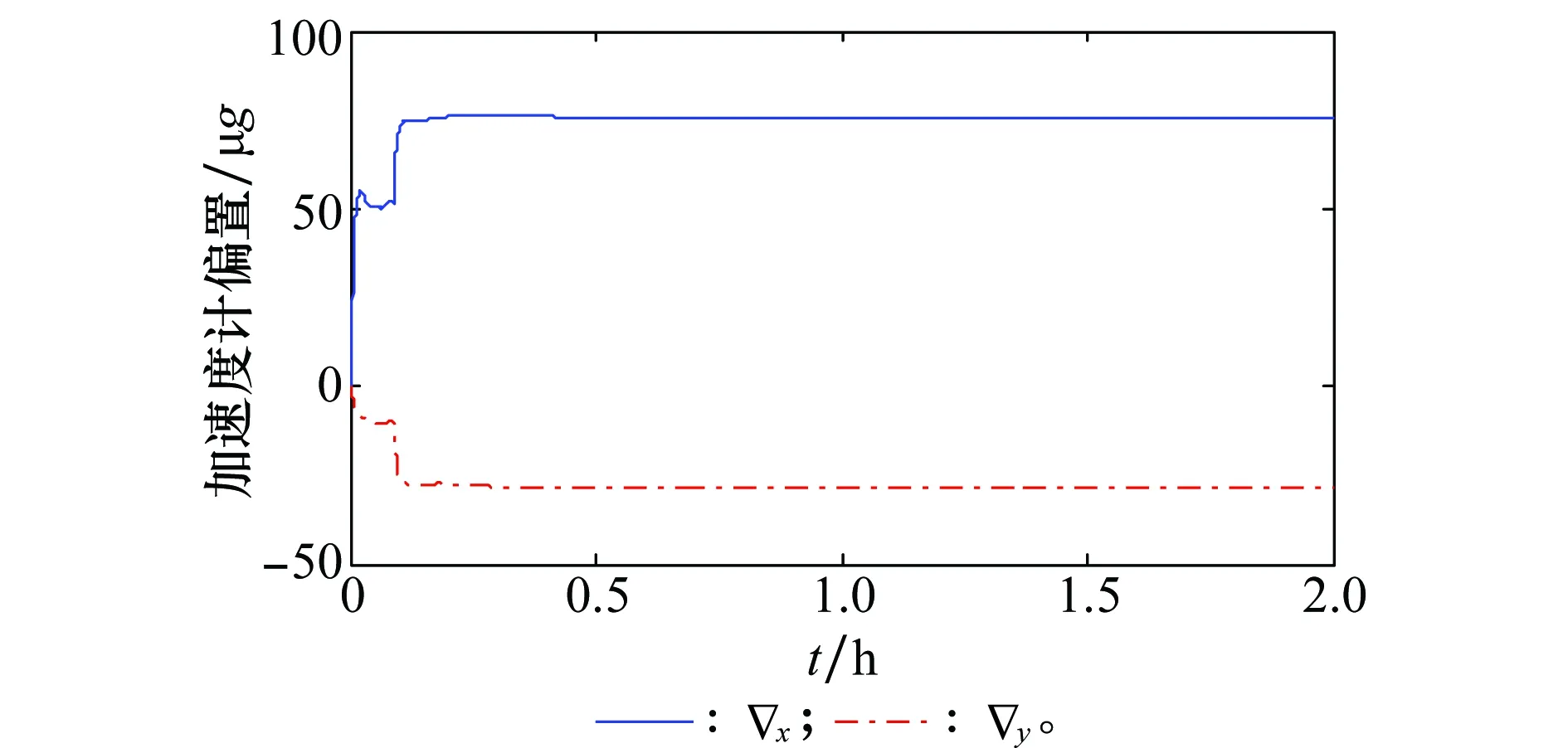
图7 加速度计偏置估计曲线Fig.7 Estimation curves of the accelerometer biases

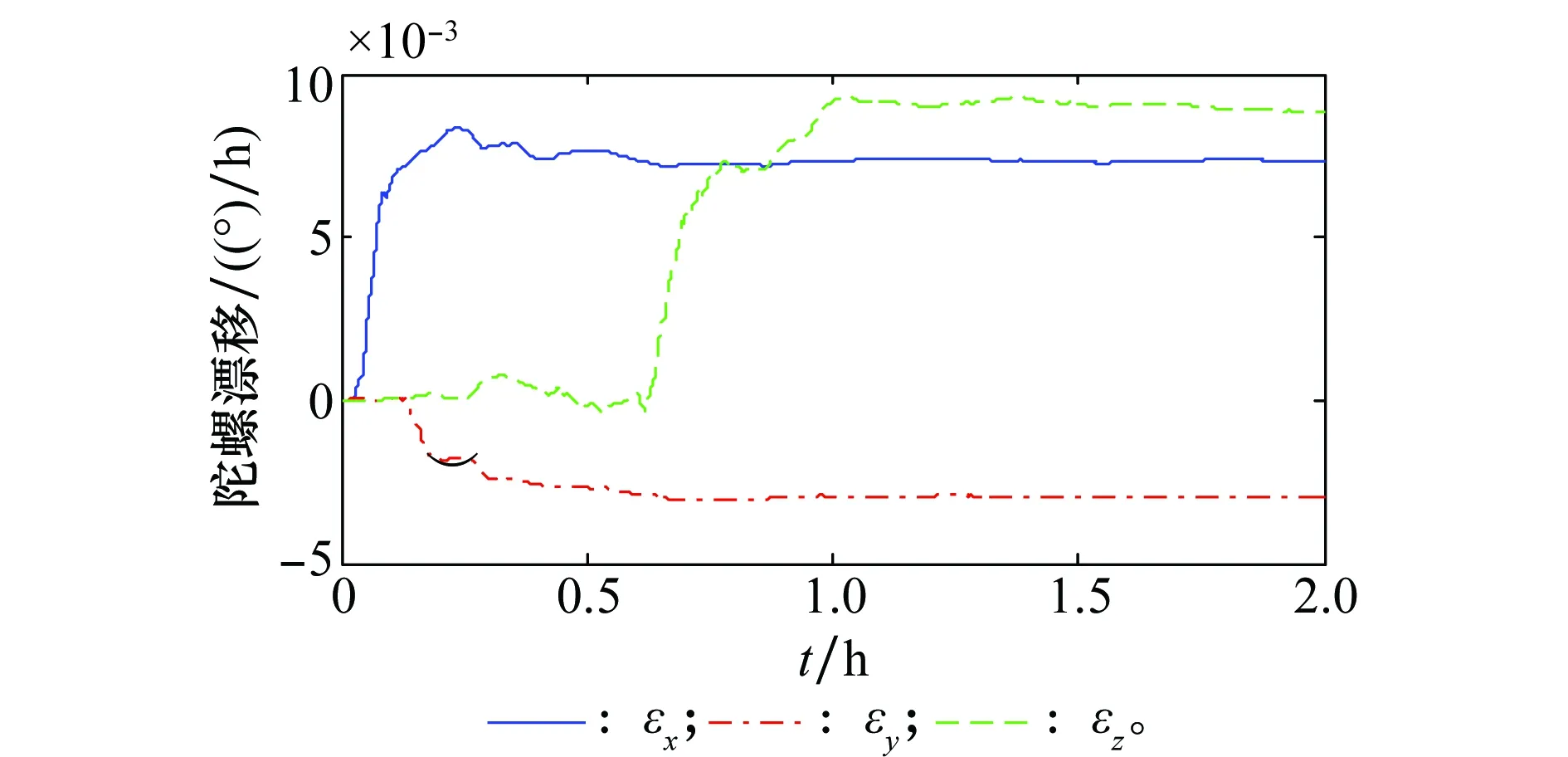
图8 陀螺漂移估计曲线Fig.8 Estimation curves of the gyro drifts

由图7～图9可以看出,在单轴旋转SINS中,转动IMU提高了系统的可观测性,将SINS中加速度计偏置与东向陀螺漂移由不可观测变为可观测,同时利用本文所给出的方法有效估计得到方位轴陀螺漂移以及标度因数误差。

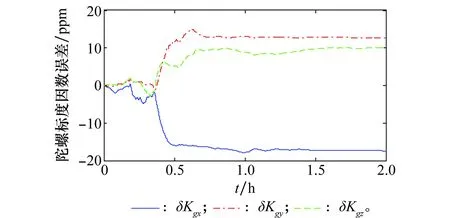
图9 陀螺标度因数误差估计曲线Fig.9 Estimation curves of the gyro scale factor errors

为了进一步验证结果的准确性,车载验证实验在完成IMU误差估计补偿后进行了12 h导航实验,图10为有无补偿IMU误差前后位置误差对比曲线,图中红色点画线是系统实际解算得到的12 h位置误差曲线,蓝线为利用保存的数据离线计算得到的未补偿IMU误差时的12 h位置误差曲线。

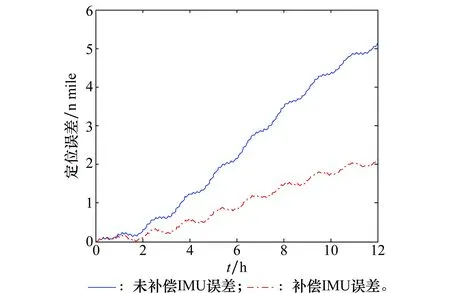
图10 位置误差对比曲线Fig.10 Position error comparison curves

由图10可以看出,IMU误差经过标校补偿后,惯导系统12 h位置误差由5.13n mile减小为2.12n mile,系统定位精度提高了58.7%。

5 结 论

本文首先给出了单轴旋转SINS误差调制原理,分析了影响方位陀螺漂移估计精度的主要误差因素,指出东向陀螺漂移和方位失准角是其中影响最大的两个误差源。由于陀螺标度因数误差在单轴旋转SINS中无法被调制,因此将此项误差也加入到标校模型中。对传统Kalman滤波器进行了优化,设计了一种合理的估计流程以较为全面地对系统中的各项误差进行估计。

利用单轴旋转SINS进行了转台摇摆和车载行进间验证实验,由误差估计曲线可以看出,经过一段时间后IMU误差能够得到有效估计。车载验证实验完成IMU误差估计后转入到纯惯性导航,系统定位精度提高了58.7%,由此验证了该方法的有效性和可行性。