基于分段贝塞尔曲线的多导弹协同航迹规划

王晓芳, 柴 劲, 周 健

(1. 北京理工大学宇航学院, 北京 100081; 2. 中国兵器工业第二〇三研究所, 陕西 西安 710000)

0 引 言

目前,战争在向信息化、智能化方向发展,未来的战争必然是系统与系统、体系与体系的对抗,此时,单枚导弹的作用将显得非常有限,多枚导弹协同作战将成为未来战争的必然趋势[1-3]。如果多枚导弹在保证自己生存能力的前提下,能够从不同方向同时对目标进行攻击,则能大大提高导弹的末段突防和攻击能力。

航迹规划是实现多弹突防和协同攻击的核心技术[4-5]。从目前已公开的文献看,对单个飞行器的航迹规划算法的研究较多,采用的方法主要有A*算法[6-8]、改进混合整数线性规划法[9]等经典算法和遗传算法[10-12]、蚁群算法[13]、萤火虫算法[14]等现代智能优化算法。相对于单飞行器航迹规划技术,多飞行器的航迹规划则需要考虑协同飞行时间、飞行器间避免碰撞等更多的问题。文献[15]基于分层结构法设计了航迹规划层与协同任务层,基于Voronoi图和Djikstra 搜索算法生成了满足无人机运动学约束且使无人机暴露在敌方雷达探测范围内时间最短的协同航迹,实现了多无人机的协同集结。文献[16]中假设无人机间存在模糊虚拟斥力并据此设计算法生成了能够同时避免与障碍和其他无人机碰撞的航迹,然后通过各无人机调整速度又实现了同时到达目标的目的。文献[17]基于改进的遗传算法,为从同一平台发射的多枚导弹生成了满足运动学约束、导弹飞行安全约束以及最小发射间隔时间约束的协同航迹。文献[18-20]则分别采用了粒子群算法、蚁群算法以及Tau理论等仿生算法为多飞行器生成了满足任务约束(集结、编队)、安全约束(防碰撞)的协同航迹。上述多飞行器协同航迹规划算法中,主要考虑了对多飞行器协同飞行时间的约束,并没有考虑对协同飞行方向进行约束,而多飞行器如果能从指定的方向同时到达目标则会进一步增强其突防能力和对目标的毁伤能力。同时,上述算法中得到的都是由航迹节点构成的航迹折线段而非飞行器实际的可飞航迹,需要进一步考虑飞行器的运动学特性对航迹进行光滑以得到可飞航迹,但是在某些节点处可能出现由于过载限制等原因导致航迹无法光滑过渡的情况。

近年来,贝塞尔曲线由于其简单易设计、可直接生成光滑轨迹等优点被应用于航迹规划中[21-25]。文献[21]中首先将轨迹规划分解为轨形规划和速度规划两个子问题,基于4次贝塞尔曲线为无人车规划了满足曲率连续、速度连续、加速度连续等多种约束条件的轨迹。文献[22-23]考虑飞行环境中的障碍,基于分段贝塞尔曲线分别基于滚动时域法和“分层优化结构”生成了可使飞行器避障的多段航迹。文献[24]则侧重无人机飞行过程中的突发威胁/障碍,提出了碰撞预测与航迹重规划的方法。但上述文献并未考虑多个飞行器协同飞行的问题。文献[25]针对多架无人机先设计了满足运动学约束、曲率挠率约束以及防碰撞约束的5次贝塞尔曲线航迹,再以二次贝塞尔曲线为模型设计了各无人机的速度曲线,实现了多无人机同时到达。但文献中并未考虑多无人机协同飞行方向的约束,另外,通常而言导弹的速度调整与控制不如无人机灵活,因此这种通过设计速度方案实现时间协同的方法也并不适用于多枚导弹作战的情景。

本文同时考虑多导弹飞行时间协同和攻击方向协同的问题,基于贝塞尔曲线建立了航迹模型,通过威胁区建模、可行航迹节点选取、分段贝塞尔航迹优化及调整、协同航迹时空安全性判断和航迹重生成等步骤,得到了能够避免环境中的威胁以及多导弹间的相互碰撞且满足导弹过载约束的协同航迹,并通过仿真验证了本文算法的有效性。

1 导弹的贝塞尔曲线航迹模型

假设导弹在二维平面的航迹为贝塞尔曲线,其质心坐标X=[x,y]T可表示为

(1)

式中,bi为控制点二维坐标;n表示曲线次数;τ∈[0,1]为参数;Bi,n(τ)为伯恩斯坦多项式,其表达式为

(2)

第一个控制点b0与导弹的起始位置重合,最后一个控制点bn与导弹的终点重合。贝塞尔航迹曲线在起点与终点处的切线方向分别与向量b0b1,bn-1bn一致,因此,可通过设置控制点bn-1来控制导弹攻击目标的方向。

为实现满足任意给定起点终点以及攻击方向约束的航迹构造,本文采用3次贝塞尔曲线[26]即n=3,如图1所示。

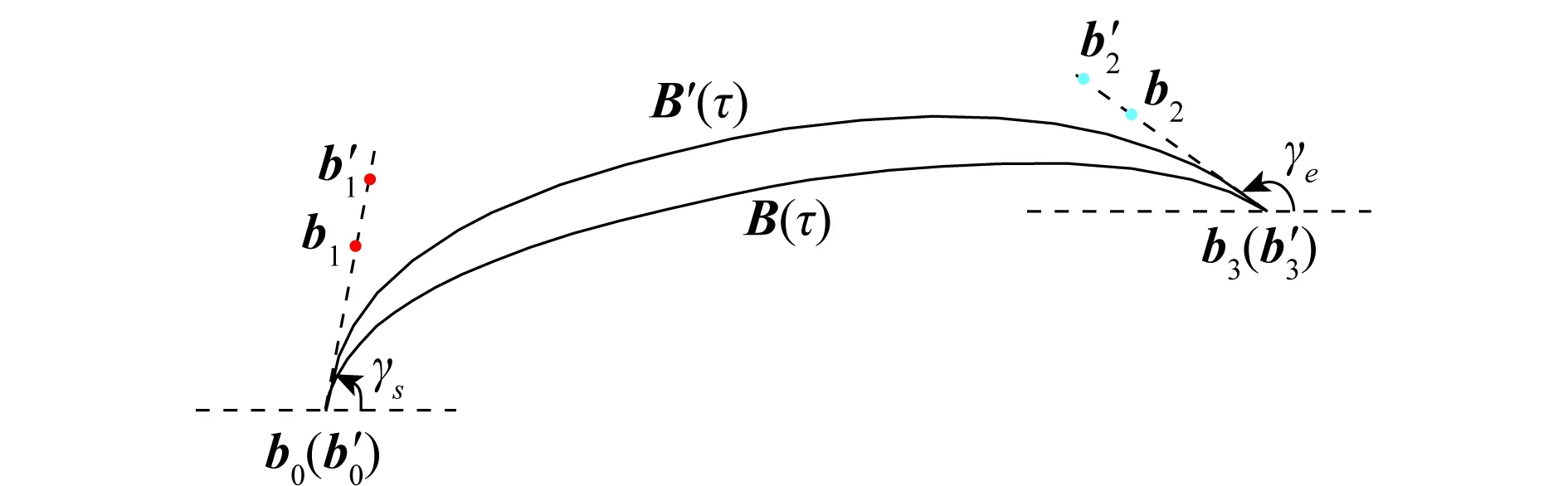
图1 3次贝塞尔曲线控制点与曲线关系示意图Fig.1 Diagram of Cubic Bezier and its control points

图中,B(τ)为基于b0,b1,b2及b3的3次贝塞尔航迹曲线。假设导弹的起点发射角为γs、末端攻击角为γe,其与b0b1,b2b3斜率ks、ke的有如下关系:

(3)

式(1)为表征导弹贝塞尔曲线航迹的参数方程,可根据其计算得到航迹长度为

(4)

假设导弹的速度为V,导弹航迹上每一点的需用法向过载nR为

(5)

本文中,导弹的航迹由几段3次贝塞尔曲线连接而成。假设导弹的速度为常值,要求多枚导弹同时以指定的角度攻击目标。攻击角度约束的满足通过导弹最后一段贝塞尔曲线的第3个控制点b2的设置来实现。攻击时间约束的满足则通过要求每枚导弹的航迹长度l相等来实现。在设计每枚导弹的航迹时,要考虑威胁区回避、路径最短以及航迹连接点过载近似连续的问题。

2 协同航迹规划算法

首先考虑由几段贝塞尔曲线构成的单枚导弹的航迹的设计,然后再综合考虑多枚导弹航迹长度要一致的协同航迹设计问题。在设计单枚导弹的航迹时,要考虑回避威胁区,而且要考虑组成航迹的几段贝塞尔曲线长度较短且端点过载较小,因此,涉及到环境中威胁区位置确定,分段贝塞尔曲线首末端点确定,以及在确定端点前提下贝塞尔曲线的优化问题。由于本文中分段贝塞尔曲线首末端点确定和每段贝赛尔曲线航迹的优化是结合进行的,这里首先阐述在首末端点已确定前提下的贝塞尔曲线的优化问题。

2.1 分段贝塞尔航迹优化

对于每一段3次贝塞尔曲线航迹,由于分段起点S与分段终点E分别与第1个控制点b0与第4个控制点b3重合,因此只要确定剩余2个控制点b1、b2就可确定整条航迹。在导弹分段起点速度方向和分段终点速度方向确定的前提下,由式(2)即可确定b0b1、b2b3方向。进一步只要确定其长度|b0b1|、|b2b3|,就可确定2个控制点的位置,因此,将|b0b1|、|b2b3|设为优化问题的设计变量。

考虑到路径尽量短以及航迹端点过载尽量小的问题,性能指标函数设为

minf=lBi(τ)

(6)

式中,lBi(τ)表示第i段航迹的长度,可由式(3)计算得到。

导弹在飞行过程中,其法向过载不能超过导弹的可用过载nP,另外,导弹航迹上的每一点与威胁区的距离必须要大于最小安全半径,因此有约束

|ni(τ)|max≤nP

(7)

d(τ)i,j≥rdj

(8)

式中,|ni(τ)|max为第i段曲线上的最大需用过载;d(τ)i,j为第i段曲线上每一个点与第j个威胁中心的距离;rdj为其最小安全半径。

为使分段航迹连接处过载近似连续,设置如下的连接点过载约束:

(9)

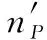
至此,得到了确定第i段贝塞尔曲线航迹的优化问题,即

minf(|b0b1|,|b2b3|)=lBi(τ)

(10)

求解如式(10)所示的非线性约束优化模型即可得第i段长度最短、满足可用过载约束、可避免威胁区且可对航迹连接点过载进行控制的贝塞尔曲线航迹。

2.2 具有攻击角度约束的单枚导弹多段贝塞尔曲线航迹设计

将环境中的威胁区、禁飞区等不规则外形区域等效为一个半径为ro的圆区域,考虑安全余量rs>0,每个威胁区的最小安全半径可定义为

rd=ro+rs

(11)

假设导弹飞行的环境中有m个威胁区,其等效圆的圆心为Oj(j=1,2,…,m)、最小安全半径为rdj(j=1,2,…,m)。应用德劳内三角法[27]连接威胁区等效圆的圆心,之后进行有效边的判定:如果两个圆心的连线不经过某个威胁区,则这条边为“有效边”,否则为“无效边”。将无效边从德劳内三角法所构造的三角连接图中去除,并定义有效边在威胁区圆外部分的中点为导弹可经过的航迹点,由此得到除了起始点和目标点外导弹的其他航迹节点集合为

定义导弹经过此点时的飞行方向单位矢量α满足

(12)

式中,Ow,j1j2e表示当前航迹节点指向目标点e的向量；Oj1Oj2表示由距离目标较远的威胁区圆心指向距离目标较近的威胁区圆心的向量,即满足|Oj1e|>|Oj2e|。这样定义的飞行方向可使导弹垂直于障碍中心连线朝向目标飞行。

当飞行环境中存在多个障碍时,上述航迹节点集W包含较多元素。在为某枚导弹进行航迹规划时,不必对集合中所有航迹节点进行考察,特别是那些明显使导弹绕远的航迹节点。因此,提出导弹相关航迹节点集的概念。

导弹相关航迹节点集:假设有N枚导弹,其起点分别为sk(k=1,2,…,N)。对于第k枚导弹,相关航迹节点集Wk定义为:连接起点sk与目标点e的线段与障碍分布德劳内三角连接图所有相交边上的航迹节点构成的集合。

为降低航迹复杂性,提高规划速度,原则上航迹所经过的节点数目越少越好。最好情况为仅由一段从起点到达目标的贝塞尔曲线。因此,在设计航迹节点选取算法时,每次迭代均优先以目标为分段终点。若以目标为分段终点无满足约束条件的航迹,则应在导弹相关航迹节点集中选择距离目标较近的航迹节点作为分段终点。以上述选点原则,设计第k枚导弹的航迹节点选取算法如下:

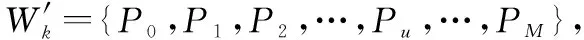
(2) 定义分段航迹的起点为S、终点为E,寻找可行点集Pick及不可行点集Ban。初始时,有S=sk、E=e、Pick={sk}和Ban=∅。考虑一般情况,针对起点为S、终点为E=Pu的一段航迹,采用式(9)中的模型对航迹进行优化,如果能够得到同时满足威胁区、过载、攻击角度等约束的优化解,则将Pu放入可行点集Pick中,接下来以Pu作为分段起点,P0=e作为分段终点,再进行优化;如果不能够得到优化解,则取E=Pu+1,如果Pu+1出现以下任一情况:

① 出现在可行点集Pick中(意味着导弹已经经过该点)；

② 出现在不可行点集Ban中(说明该点没有通往任何下一个点的可行航迹)；

③Pu+1的|Ow,j1j2e|大于S的|Ow,j1j2e|值(说明Pu+1点与目标的距离大于分段起点与目标的距离,导弹将往回飞)，则舍弃Pu+1,继续取下一个值Pu+2,再进行判断,直至取到满足要求的点。

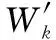
(3) 上述搜索与优化过程终止的条件

①Ban={P1,P2,…,PM},说明该任务无解;

②Pick中出现终点e,说明已经找到从导弹起点到终点的航迹,集合Pick即为得到的航迹节点集。此时,导弹k得到了一条能够避免威胁区并以指定攻击角度攻击目标的航迹。

2.3 同时满足攻击角度与攻击时间约束的协同航迹规划方法

第2.2节中得到的每枚导弹的航迹总长度是不同的,在导弹飞行速度相同的前提下,导弹到达目标的时间不同,不能满足攻击时间一致的约束。假设第k枚导弹的航迹长度为lk(k=1,2,…,N),其中最大值为lmax=max{l1…lk…}。可将其他导弹的航迹长度扩展为lmax,则可保证多导弹同时命中目标,满足攻击时间约束。以导弹1为例来说明问题。假设导弹1的航迹由三段组成即l1=ls1+l12+l2e,导弹1的航迹长度与最长航迹之间的差为Δl1=lmax-l1,则按照l1的三段航迹分别占总航迹的比例来分配Δl1有

(13)

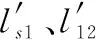
为了得到给定长度的贝塞尔曲线航迹,参考如式(9)所示的优化问题,加入关于轨迹长度的约束

(14)

构建新的优化问题为

minf(|b0b1|,|b2b3|)=|ni(0)|+|ni(1)|

(15)

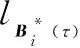
2.4 协同航迹时空安全性判断与重生成

在第2.3节中得到协同航迹后还要对航迹间的时空安全进行判断,即保证沿协同航迹飞行的几枚导弹的最小间距不小于最小安全间距。

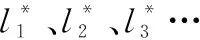
3 仿真分析

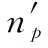
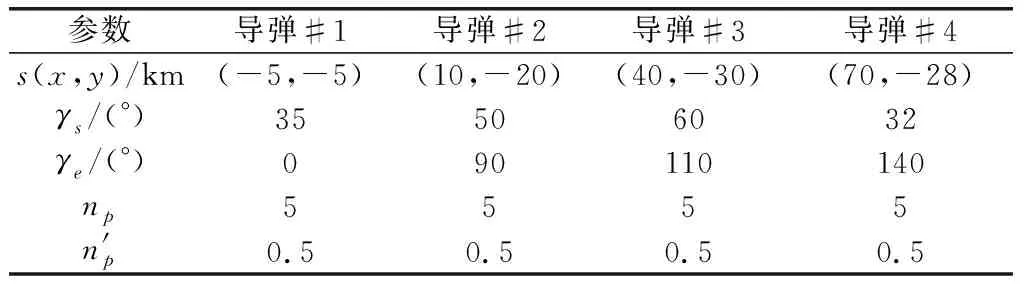
表1 导弹的初始参数、可用过载及指定的攻击角度

假设导弹飞行的环境中有7个威胁区,其具体信息如表2所示。威胁区分布如图2所示，图中,按照德劳内三角法连接威胁区的中心并绘出航迹节点(红色圆点)。

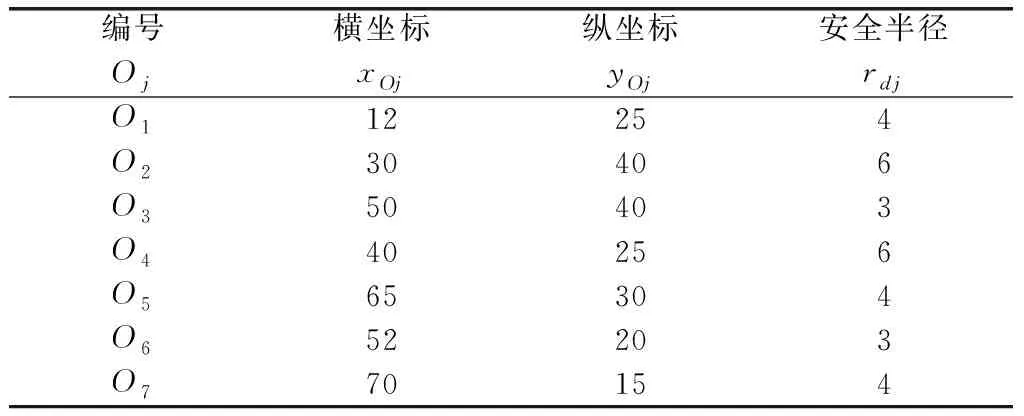
表2 威胁区中心位置及安全半径

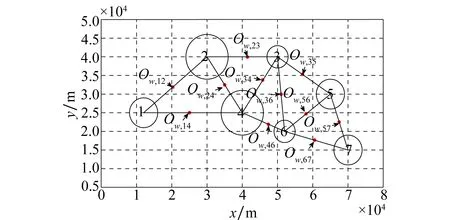
图2 战场威胁区及航迹节点图Fig.2 Threaten areas and waypoints in battleground

由图2可得到总的航迹节点集为

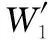
同理,得到含有目标点的导弹#2、#3和#4的相关航迹节点集合分别为

3.1 算法验证

采用Matlab非线性约束优化函数FMINCON对航迹进行优化,最大迭代次数为100。取优化变量|b0b1|、|b2b3|的初值均为分段航迹起点与分段航迹终点间的距离|SE|。设导弹间的安全距离ds=50 m。规划出的4枚导弹的航迹如图3所示。

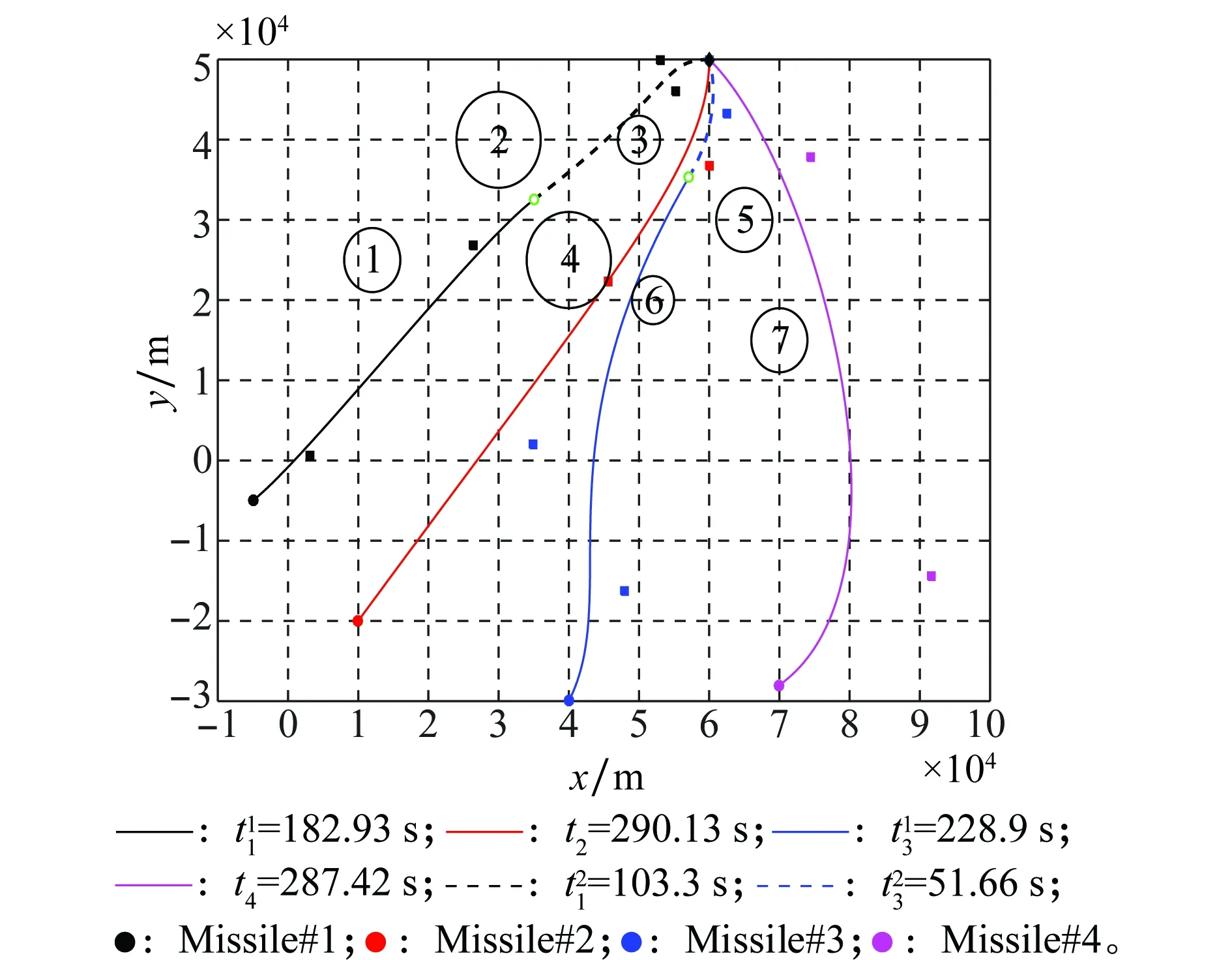
图3 导弹#1～#4的可行航迹Fig.3 Feasible paths for missile #1 to missile #4

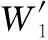
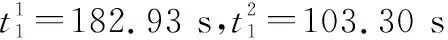
(16)

由此可见,规划好的贝塞尔航迹满足以指定发射角发射导弹和以指定角度攻击目标的要求。

类似地,对于导弹#2,其可行航迹点集为Pick2={s2,e},因此,图3中,导弹#2的航迹是一条连接起始点和终点的航迹,中间没有经过其他航迹点。导弹#2的飞行时间为t2=290.13 s,航迹第三个控制点的位置为(60,36.71)km,满足攻击角度为90°的要求。导弹#3、#4的可行航迹节点集分别为Pick3={s3,Ow,35,e}、Pick4={s4,e},导弹总飞行时间分别为t3=280.56 s、t4=287.42 s,导弹#3第二分段航迹以及导弹#4航迹的第三个控制点位置分别为(60.05 km,49.87 km)、(74.42 km,37.89 km),同样满足攻击角度110°和140°的要求。

导弹#1～#4各段航迹的对应过载如图4所示。

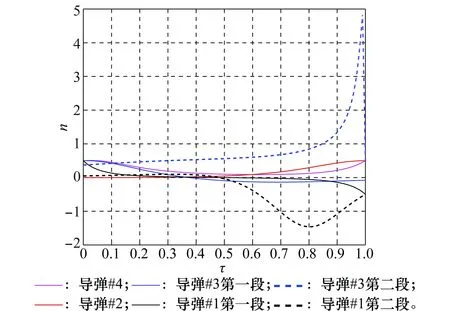
图4 导弹#1～#4的过载随参数τ的变化曲线Fig.4 Overload VS parameter τ for missile #1 to missile #4

由图4可见,4枚导弹的最大需用过载均小于等于5,未超过可用过载np且在航迹端点(即τ=0与τ=1时)处过载均小于等于0.5。

由前述可知,4枚导弹的飞行航迹长度不相等,不能够实现时间协同。其中,导弹#2的航迹最长,因此,导弹#2的航迹不作调整,由于各导弹速度均为300 m/s,可将式(12)中航迹长度l替换为时间,故其余各导弹的各段航迹飞行时间分别调整为

(17)

上述调整后的时间乘以速度得到的航迹长度即为导弹#1、#3和#4各段航迹的期望长度lB*(τ)。采用式(14)中的优化模型进行优化,得到如图5所示的调整后的航迹。

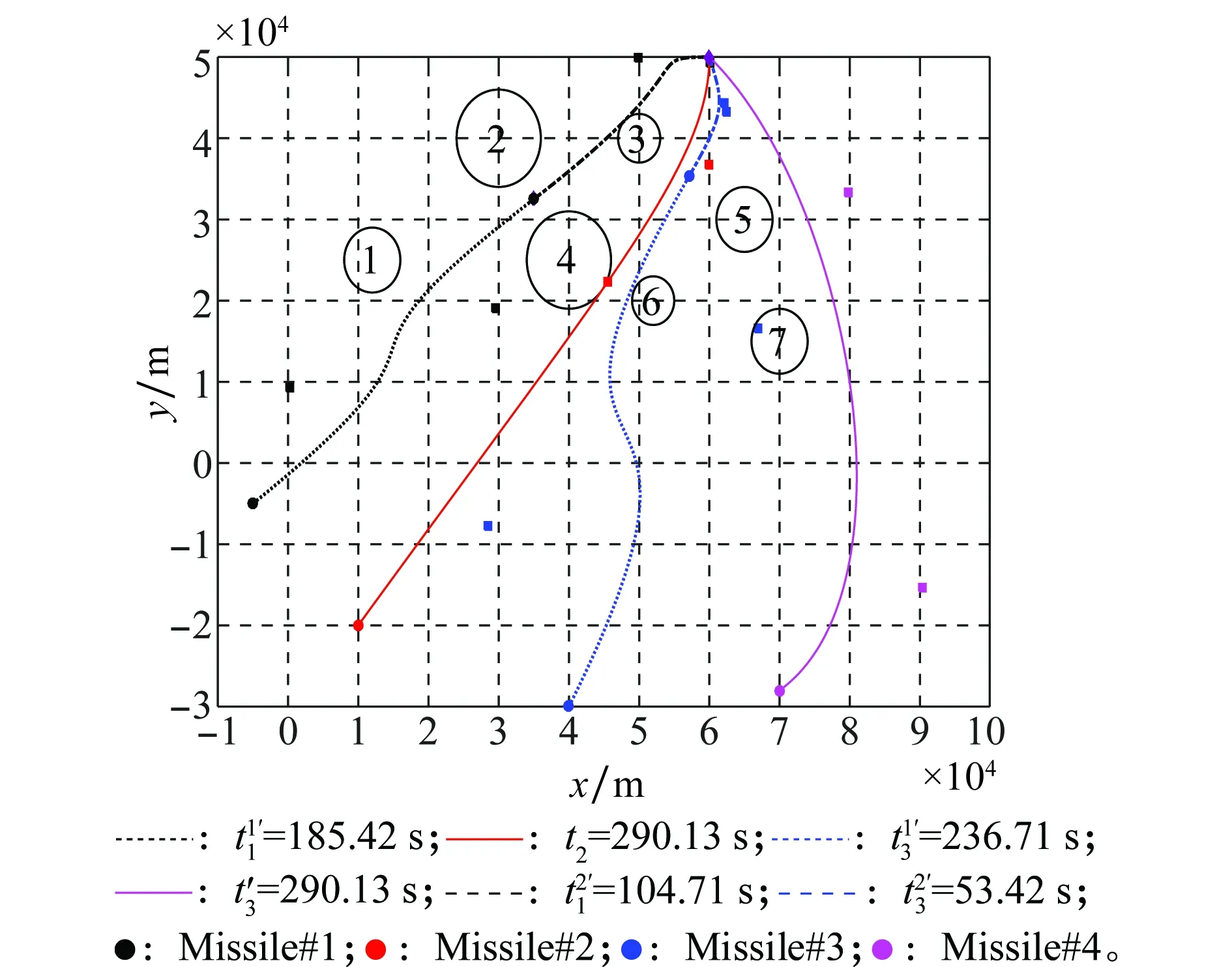
图5 导弹#2的原航迹与导弹#1、#3和#4调整后的航迹Fig.5 Original paths for missile #2 and adjusted path formissile #1、#3 & #4

由仿真结果可知,调整后的导弹#1、#3、#4的航迹依然满足发射角度与攻击角度的约束。但由于控制点位置改变,新的航迹曲率和长度均有变化,在满足攻击角度约束的基础上进一步满足了攻击时间的约束。调整后各导弹飞行航迹等长,飞行时间相等,均为290.13 s。由于导弹#1、#3和#4要通过绕路来增大其航迹长度,因此调整后的3枚导弹的最大需用过载稍微增大,但仍小于可用过载,满足过载约束。

图5中4枚导弹除了在终点处相交其余航迹位置均不相交,且导弹#2、导弹#3航迹中段的最小距离约为1.8 km远大于最小安全距离ds=50 m。因此,4条协同航迹是满足时空安全性要求的。

如假设导弹#1、导弹#4的理想攻击角度分别为90°和30°,为了说明问题的简洁性,只为导弹#1和导弹#4规划协同航迹,得到的航迹如图6所示。

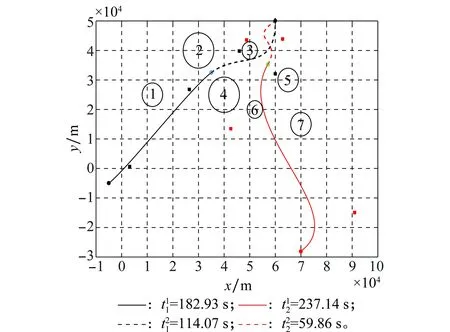
图6 导弹#1和导弹#4的协同航迹Fig.6 Cooperative path for missile #1 and missile #4

由图6可见,两枚导弹的第二段航迹存在交叉,交叉处τ1=0.773,τ2=0.319,则根据式(3)可算得从起点至交叉点的路程,进而算得两枚导弹在交叉处的飞行时间分别为266.9 s和258.64 s,可见两枚导弹并非同时到达航迹交叉处,导弹#4到达交叉处8.26 s后导弹#1才到达,因此所规划航迹也是安全的。

需要说明的是,考虑到多导弹之间避免碰撞的问题,导弹发射位置应尽量选择散开的位置,给各导弹指定的理想攻击角度要和导弹的发射位置相对应(尽量避免图6所示情况)。这种情况下,不安全航迹发生的可能性比较低,如果出现不安全航迹的情况,则可按照本文2.4节的方法对航迹进行重规划。

3.2 算法对比

将本文的算法与基于A*的具有攻击角度约束的航迹规划算法进行对比。A*算法是一种经典的启发式搜索算法,其通过扩展节点的方式进行航迹搜索,直到搜索至目标点。一般的A*算法不能对攻击角度进行约束,本文通过在飞行末端设置一个很小的角度范围来实现该约束。在满足导弹速度和过载要求的条件下,设置搜索步长为0.8,转弯角为±30°,扩展节点为3个,收敛角度为±1°。图7显示了两种方法下导弹#1—导弹#4具有攻击角度约束的航迹(实线为A*算法所得航迹,虚线为本文分段贝塞尔曲线航迹)。

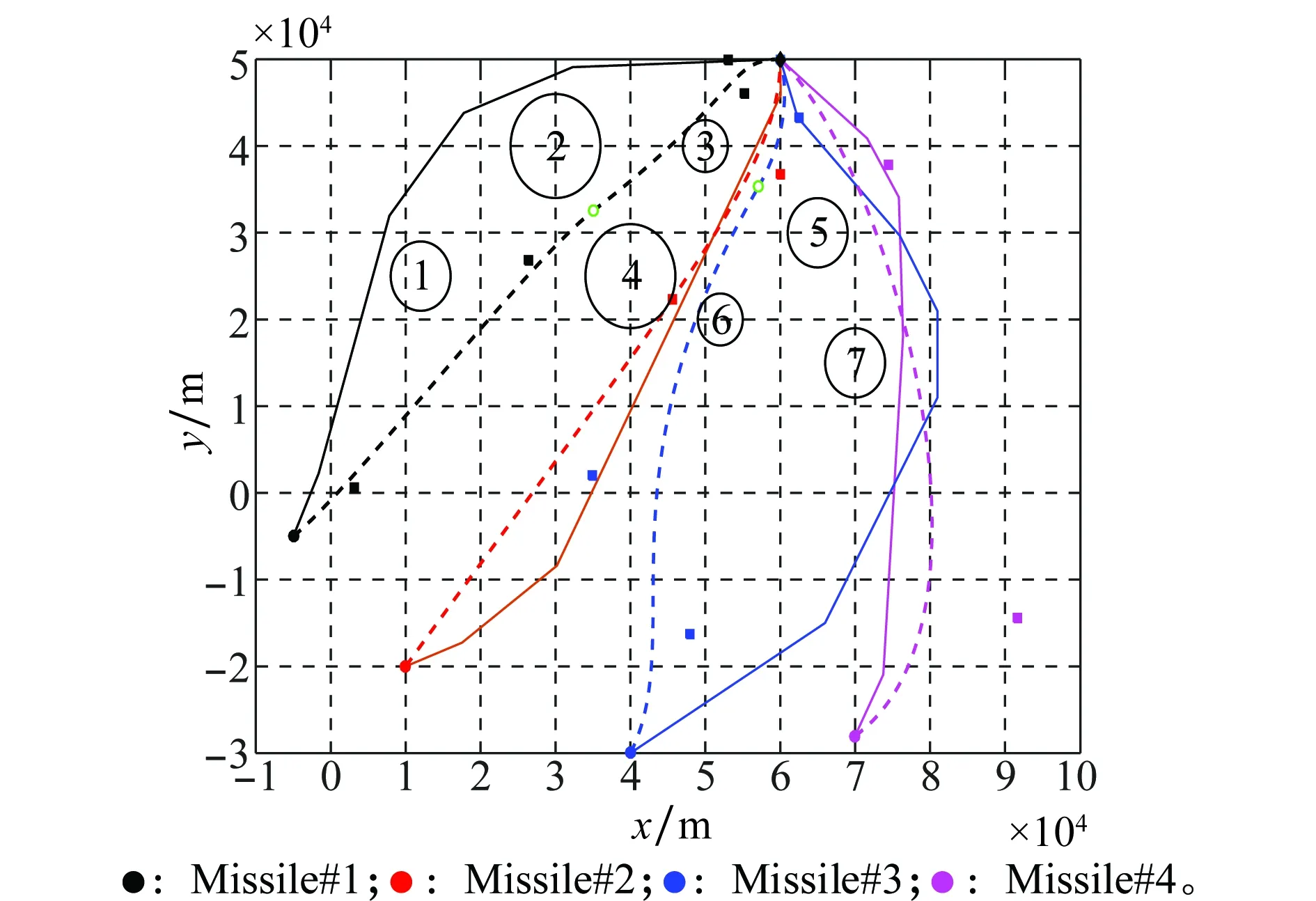
图7 A*算法所得航迹与分段贝塞尔曲线航迹对比Fig.7 Comparison of A* algorithm path and piecewise Bezier curve path

由图7可见,分段贝塞尔曲线航迹比A*算法所得对应航迹长度短,且航迹光滑。此外,两种方法下,导弹#2和导弹#4的航迹较为接近,其余两枚导弹的航迹有较大的差别,这是由于两种方法的设计思路不同造成的。A*算法搜索时,为了满足最终的角度约束,会选择从容易完成收敛的方向进行航迹节点扩展,同时,威胁区域与目标的位置关系、搜索步长都会影响航迹的生成。分段贝塞尔曲线航迹则与总的航迹节点集的选取、每枚导弹相关航迹节点集的选取有很大的关系。从算法速度方面讲,两种方法下4条航迹的规划时间对比如表3所示。

表3 两种方法下各条航迹规划时间对比

由表3可见,基于A*的算法比本文基于分段贝塞尔曲线的算法耗时要长得多。这是由于,为了满足攻击角度约束,基于A*的算法要进行大量的搜索:如果之前正向搜索至末端,不满足角度约束,则会返回上一节点重新调整方向进行搜索,如此不管尝试、重复,而且威胁距离目标较近,更不容易搜索到满足攻击角度约束的节点,进一步使搜索次数增多。而对于本文中基于贝塞尔曲线的航迹规划算法来讲,可行航迹节点集根据威胁的位置已经事先选好,而满足攻击角度约束的控制点较多,只是通过优化来得到使得分段航迹最短的控制点位置,不存在反复尝试、重复搜索的过程,因此耗时要短得多。此外,基于贝塞尔曲线的航迹规划算法直接产生满足导弹最大可用过载约束的光滑航迹,而A*算法则需要根据产生的航迹点,同时考虑导弹的最小转弯半径再对航迹进行光滑处理,会进一步增加算法的步骤和耗时。

在协同性方面,基于上述具有攻击角度约束的A*航迹规划算法在进行航迹拓展以得到满足攻击时间约束的航迹时,需要进行不断的搜索、尝试,因此会增长耗时。相比较而言,本文中基于贝塞尔曲线的航迹规划方法具有设计简单、耗时短、对威胁位置不敏感的优点。

4 结 论

本文基于分段3次贝塞尔曲线提出一种多导弹在飞行过程中能够避免威胁区,同时能够从指定的方向同时攻击目标的协同航迹规划方法。通过对贝塞尔曲线控制点的优化,得到能够满足攻击角度约束同时满足过载约束和威胁避免要求的分段贝塞尔航迹。针对给定战场中的威胁情况,设计了节点选取与分段航迹优化相结合的方法,得到了多弹满足攻击角度约束的航迹。在导弹速度相同的背景下,将攻击时间的一致等价于各弹航迹长度的一致。通过比例延长法将各导弹的航迹长度延长至多导弹中的最大航迹,再通过求解具有航迹长度约束的优化问题,得到同时满足攻击角度和攻击时间约束的多导弹协同飞行航迹。最后检测协同航迹的时空安全性即导弹间是否会发生碰撞,并给出了对于不安全航迹的调整和重规划方法。仿真中通过与基于A*算法对比,体现了本文算法设计简单、耗时较短、可直接生成满足导弹最大可用过载约束的光滑航迹等优点。