机载导弹大机动弹射发射动力学特性分析

2018-10-15张士卫

系统工程与电子技术 2018年10期

刘浩, 周军, 张士卫

(1. 西北工业大学航天学院, 陕西西安 710072;2. 中国空空导弹研究院主机部, 河南洛阳 471009)

0 引言

为了追求空优性能,隐身战机需要在大机动条件下实现空空导弹的内埋式弹射发射,以实现载机的全包线发射能力。对载机大机动条件下的导弹内埋弹射发射动力学进行研究具有重要的理论意义和工程应用价值。现今相关文献主要集中于载机平飞状态下的导弹弹射发射动力学研究,对载机大机动条件下的导弹弹射发射动力学研究还少见报道。张群峰等[1]采用重叠网格技术,对载机平飞状态下的亚声速和超声速来流的外挂投放和内埋投放进行了数值模拟。薛飞等[2]在0.6 m×0.6 m量级亚跨超声速风洞开展了载机平飞状态下的内埋武器弹射试验技术研究。刘浩等[3]采用模态离散法结合拉格朗日动力学方程研究了载机大过载条件下的弹射分离动力学特性,没有考虑科氏力对发射安全性的影响。朱收涛等[4]利用计算流体软件FLUENT和湍流模型建立了载机投弹流场数值模拟仿真模型,研究了载机平飞状态下的导弹分离过程轨迹。王许可[5]建立了机载内埋发射装置刚柔耦合动力学仿真模型,分析了发射装置主要结构设计参数对弹射分离姿态的影响;许斌[6]建立了气动弹射发射系统的动力学模型,研究了气动驱动力对弹射分离参数的影响。国外学者也对机载导弹的弹射分离进行了较多的研究[7-9],并取得了一定的成果。

针对目前载机大机动条件下的导弹弹射发射动力学研究的不足,并考虑到多刚体动力学模型已无法模拟导弹高速弹射过程中的发射机构的柔性变形,本文基于有限元法和多体柔性系统Lagrange动力学方程并考虑了弹射发射装置刚-柔-气-液耦合效应,建立载机大机动下的发射装置弹射导弹的发射动力学模型,并仿真分析了在发射装置弹射机构推动下的导弹分离速度和角速度,结果表明载机大机动发射时离心力对导弹分离角速度有负面影响;科氏力对发射装置航向受力具有负面影响,可造成其航向结构失效,影响发射安全性。在对导弹弹射发射动力学的研究中,往往会疏忽或忽略科氏力对导弹发射产生的影响,本文提出载机大机动发射研究时必须考虑科氏力。本文也可为先进战机新型战术研究提供理论指导。

1 发射动力学模型建立

考虑到弹射发射装置+导弹这一综合系统的复杂性,本文采用有限元法和多体动力学Lagrange动力学方程相结合的方法进行系统多柔体动力学建模[10-12]。发射装置杆件结构外形设计较为复杂,因此采用有限元法对各杆件进行模态离散化,使各杆件具备柔性,为多柔体动力学模型奠定基础,为了保证各杆件有限元离散的精度,将各杆件仿真模态频率与试验模态频率对比,以修正杆件有限元模型;基于柔性多体动力学Lagrange动力学方程,在计算多体动力学软件adams中根据机构实际的运动副约束情况,对发射装置动力系统、各杆件以及导弹进行可视化组装和可视化调试;然后考虑弹射机构气液混合动力系统与发射装置相互作用的刚-柔-气-液动力学耦合效应,在组装好的发射装置与导弹的动力学模型中输入整个系统的弹射动力方程,并添加载机大机动产生的离心力和科氏力,离心力和科氏力作用于导弹的质心处。最终建立发射装置对导弹高速弹射作动的发射动力学模型。

1.1 弹射发射装置机构构型

以AMELT构型内埋弹射发射装置为研究对象,其挂装导弹状态下的构型和各构件连接关系如图1所示。导弹发射时,由高压气体蓄能器推动液压介质做功,促使水平液压缸的活塞推动活塞杆向前运动,前后y字型机构将活塞杆水平推力转换成对导弹的竖直向下的推力,导弹向下运动到一定位置时弹射机构自动解锁,导弹与发射装置分离并逐渐远离发射装置和载机,弹射机构自动收回,导弹的弹射发射过程完成。

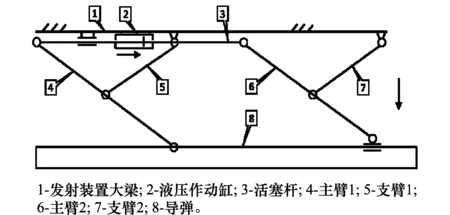
图1 已挂装导弹的AMELT发射装置结构示意图Fig.1 AMELT configuration launcher with missile

在发射装置弹射导弹的发射动力学仿真模型中,液压动力缸和导弹作为刚体处理,大梁、活塞杆、主臂1、主臂2、支臂1、支臂2作为柔性体处理。各旋转副和滑动副作为理想约束副处理。

1.2 气-液耦合弹射力模型

内埋弹射发射技术采用气-液耦合动力系统提供弹射作动力,其原理是气压蓄能+液压作动,从而实现弹射发射机构对导弹的高速作动,相对于冷气瓶弹射和抛放弹弹射方式,具有多次连续弹射免维护的显著优点。F-22隐身战机是采用气液耦合动力系统进行空空导弹弹射发射的典型代表。

(1) 蓄能器气体状态方程

蓄能器采用高压氮气进行蓄能,初始压强达到28 MPa,考虑到理想气体状态方程只对高压时存在较大误差,因此,为了高精度的模拟机载导弹弹射发射动力学,本文采用真实气体状态方程模拟蓄能器的气体压强变化,该方程考虑了高压气体分子之间的相互作用和气体分子占有的体积。

(1)

式中,p为蓄能器工作过程中的气体压强;a和b为范德瓦尔斯修正量;V0为蓄能器气体初始体积;V为蓄能器气体工作过程中的体积;n为气体摩尔数;R为理想气体常数;Q为阀门的液压流量;t为作动工作时间;T为气体绝对温度。

(2) 液压阀门流量模型

采用经典的阀门流量模型:

(2)

式中,cd为阀门流量系数,取为0.62;A为阀门有效通径面积;pye为液压弹射缸内的压强;ρ为液压油密度,取为900。

(3) 液压作动压强

在建立液压缸作动压强模型时,现有文献较少考虑液体的可压缩性,但对于高压液压系统该液体压缩量不可忽略,为了建立更准确的动力学数学模型,本文考虑液压的可压缩性,液压作动压强微分方程:

(3)

式中,A1为液压缸作动面积;v为弹射机构液压活塞运动速度;VL为液压缸当前时刻油腔体积;Eh为油液体积弹性模量。

因此,由式(1)～式(3)可知,蓄能器压强p、液压缸压强pye和弹射机构活塞速度v三者存在耦合作用,即存在:

ppyev

又由于弹射机构的大范围运动和柔性变形之间具有刚-柔耦合特点,因此本文的导弹弹射发射动力学模型考虑了刚-柔-气-液多学科耦合效应。

1.3 弹射机构多柔体动力学模型研究

本文采用有限元法和多体动力学Lagrange动力学方程相结合的方法进行系统多柔体动力学建模。

(1)动能

柔性体任意节点p的广义坐标:

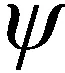
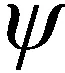
柔性体的动能包括弹射机构的动能以及导弹的动能,用如下公式表示:

式中,M(ξ)为系统质量矩阵。

(2) 势能

弹射机构变形势能W表示为

式中,K是柔性结构部件的广义刚度矩阵。

(3)多柔体动力学方程

弹射发射装置柔性动力学方程从以下拉格朗日方程求出[13-15]:

(4)

式中,Ψ为机构的约束方程;Q为投影到ξ上的广义力;λ为约束方程的拉氏乘子。

L为Lagrange项,定义为L=T-W

式(4)动力学方程可表示为

1.4 弹射发射装置杆件模态试验

机载弹射发射装置各杆件三维结构外形复杂,采用有限元法进行模态离散化时需要对各杆件局部特征如小孔、倒圆、倒边等进行简化。为了保证各杆件有限元离散化的精度,本文提出对各柔性杆件进行自由模态试验,通过模态仿真频率和模态试验频率的对比,修正杆件的有限元模型,包括修正三维模型简化程度、优化有限元网格等,为发射装置整机级的数值仿真精度奠定基础。

试验方法:用橡皮绳将试验件悬挂,达到良好的“自由-自由”的边界条件,在试验件上布置多个测试响应点并选择好激励点。采用“猝发随机”的激励方法,利用SCADAS 316系统的QDAC模块输出激励信号,采用单向加速度传感器测量响应,通过SCADAS 316系统PQFA模块采集数据[16]。利用多参考最小二乘复频域法对测到的试验数据进行处理和分析,最后得到试验件的模态频率和振型[16]。图2为弹射发射装置支臂2的自由模态试验图。

图2 支臂2的模态试验图Fig.2 Model test of the second support arm

表1和表2表明,发射装置各试验杆件模态试验频率和仿真频率在1～2阶具有很高的匹配度,说明各杆件的离散化仿真模型精度较高,限于篇幅其他各阶模态不一一列出。在弹射发射动力学整机仿真模型中,为了兼顾整机仿真精度和计算效率,各构件的截止模态一般取30～40阶。

表1 1阶模态试验频率与仿真频率对比表

表2 2阶模态试验频率与仿真频率对比表

2 发射动力学仿真分析

美国F-22隐身战机已能在5个过载的俯冲拉起大机动条件下弹射发射空空导弹。大机动发射时导弹弹射分离参数将偏离理想设计值,可能引起机构的结构破坏或失效,威胁载机发射安全性。本文仿真分析在战机5个过载的大机动条件下离心力和科氏力对导弹弹射发射分离参数的影响。表3为主要仿真参数表。

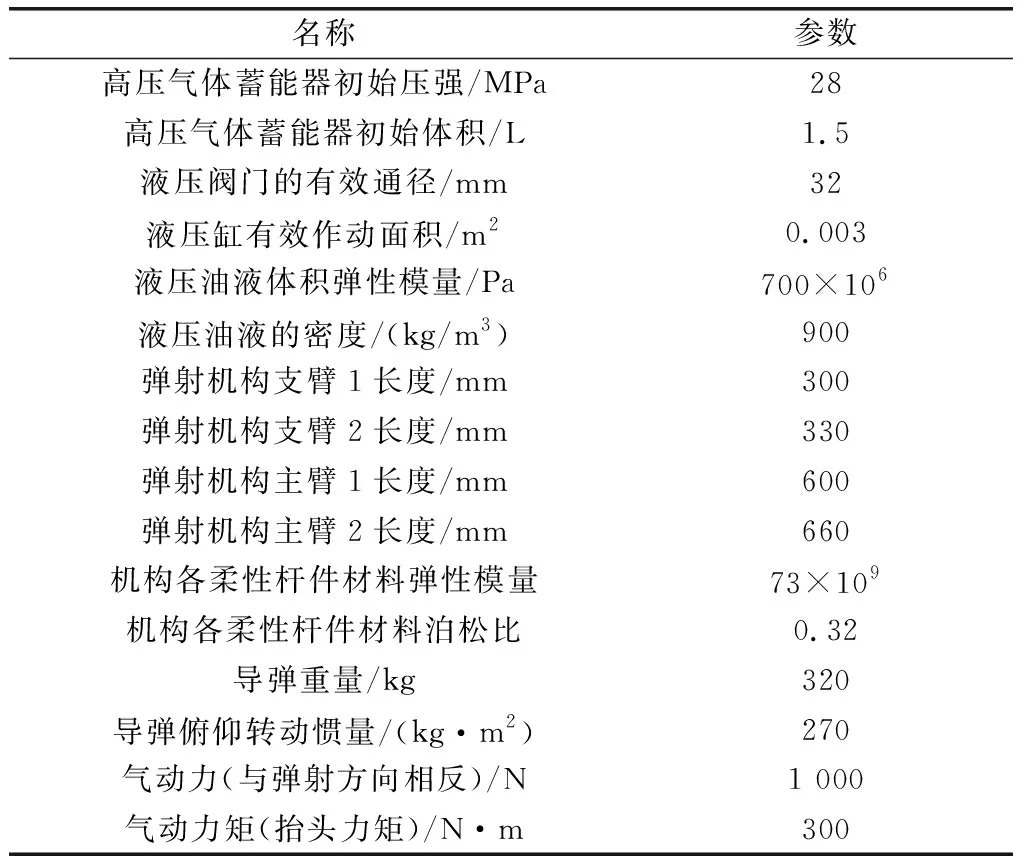
表3 主要仿真参数

2.1 气液混合动力蓄压对分离参数影响分析

一般来说,对于机载导弹弹射发射系统,安全的分离参数为:弹射分离速度≥7.6 m/s,角速度20°/s～50°/s。

图3为气液混合动力系统的蓄能器气动压强和液压作动缸的液压压强,其中虚线为气压作动压强,实线为液压作动压强。蓄能器初始气动蓄压为28 MPa,随着弹射作动的进行,蓄能器气压逐渐降低,最后为13 MPa。在弹射初始阶段液压作动缸建立压强约10 ms并达到24.7 MPa,在最后导弹分离时刻液压压强还有6.2 MPa。

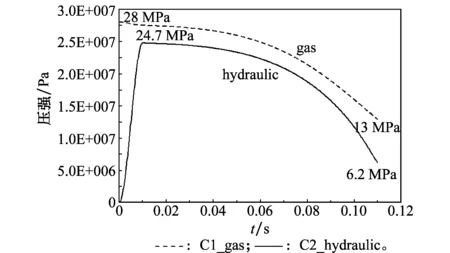
图3 气动压强和液压压强Fig.3 Gas pressure and hydraulic pressure

图4为蓄能器不同初始气动压强下的导弹弹射分离速度。如图,在当蓄能器初始压强为30 MPa时,弹射分离速度为8.37 m/s;初始压强为28 MPa时,弹射分离速度为8.04 m/s;初始压强为26 MPa时,弹射分离速度为7.85 m/s。因此,随着蓄能器初始压强的降低,弹射分离速度降低。

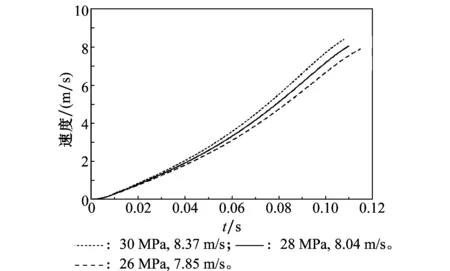
图4 不同气动压强下的弹射分离速度Fig.4 Separation velocity with different pressure

图5为蓄能器不同初始气动压强下的导弹弹射分离角速度。如图所示,在当蓄能器初始压强为30 MPa时,弹射分离角速度为31.2°/s;初始压强为28 MPa时,弹射分离角速度为32°/s;初始压强为26 MPa时,弹射分离角速度为30.8°/s。可以看出,在蓄能器初始压强28 MPa±2 MPa范围内,弹射分离角速度受蓄能器初始气动压强的影响较小。

2.2 科氏力仿真分析

当载机进行俯冲拉起大机动发射时,载机存在一个绕空中某点的角速度ω,而导弹在弹射发射装置推动下相对于载机有一个向下的相对速度v,因此,导弹相对于载机将存在科氏效应。在导弹的弹射分离行程内,导弹将受到“额外”的科氏力作用,该科氏力作用于导弹质心并沿导弹轴线指向导弹尾部。科氏力通过导弹与发射装置的机械接口传至发射装置,将影响弹射发射装置的受力和导弹的弹射分离参数。

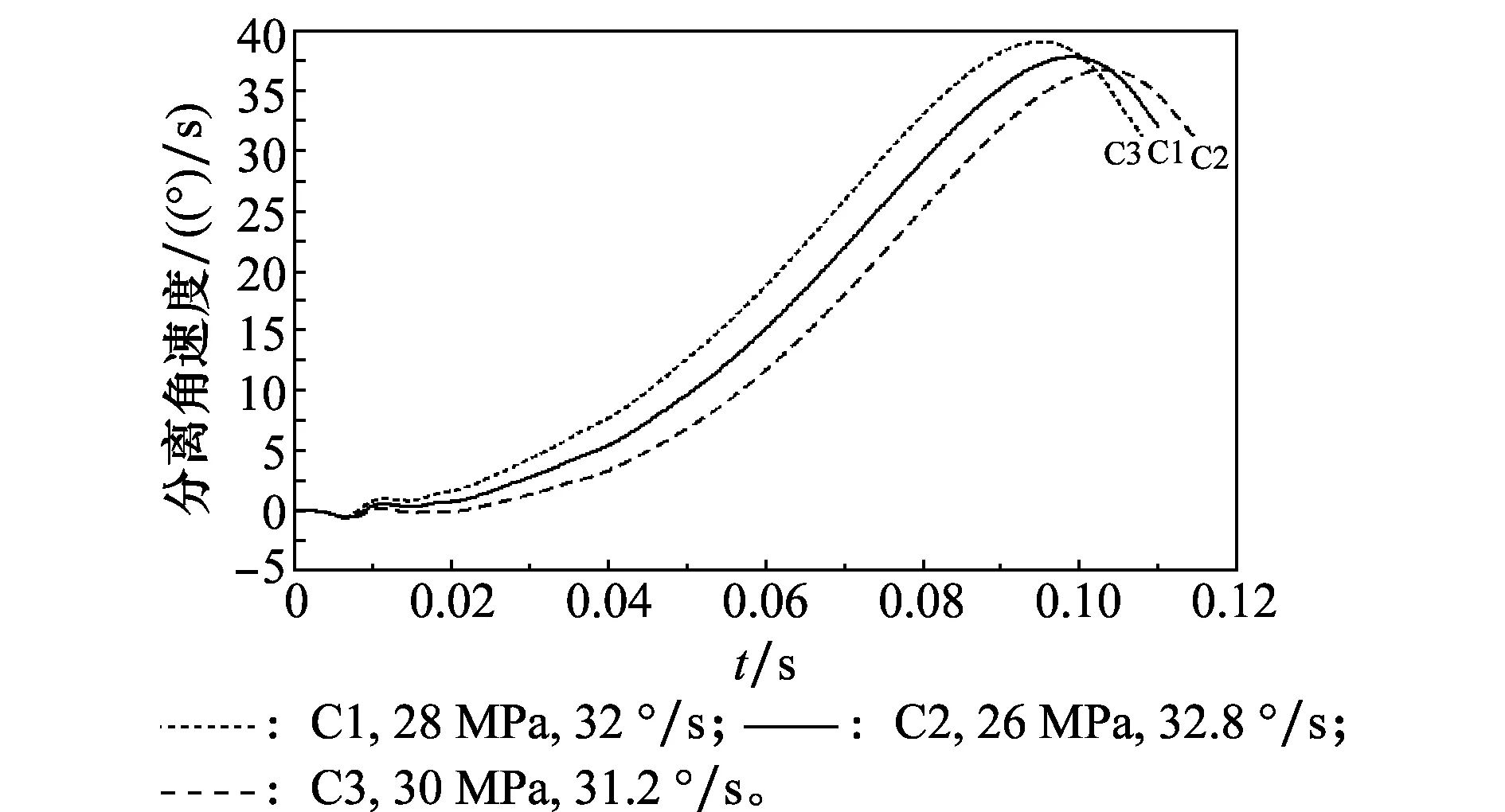
图5 不同气动压强下的弹射分离角速度Fig.5 Ejection separation angle velocity with different pressure

图6为导弹在载机5个过载大机动条件下发射时所受的科氏力,如图所示,科氏力随着时间逐渐增大,在导弹与发射装置分离时刻可达到约2 230N(曲线终点处),其主要原因在于在弹射过程中导弹相对于载机的相对速度v越来越大。

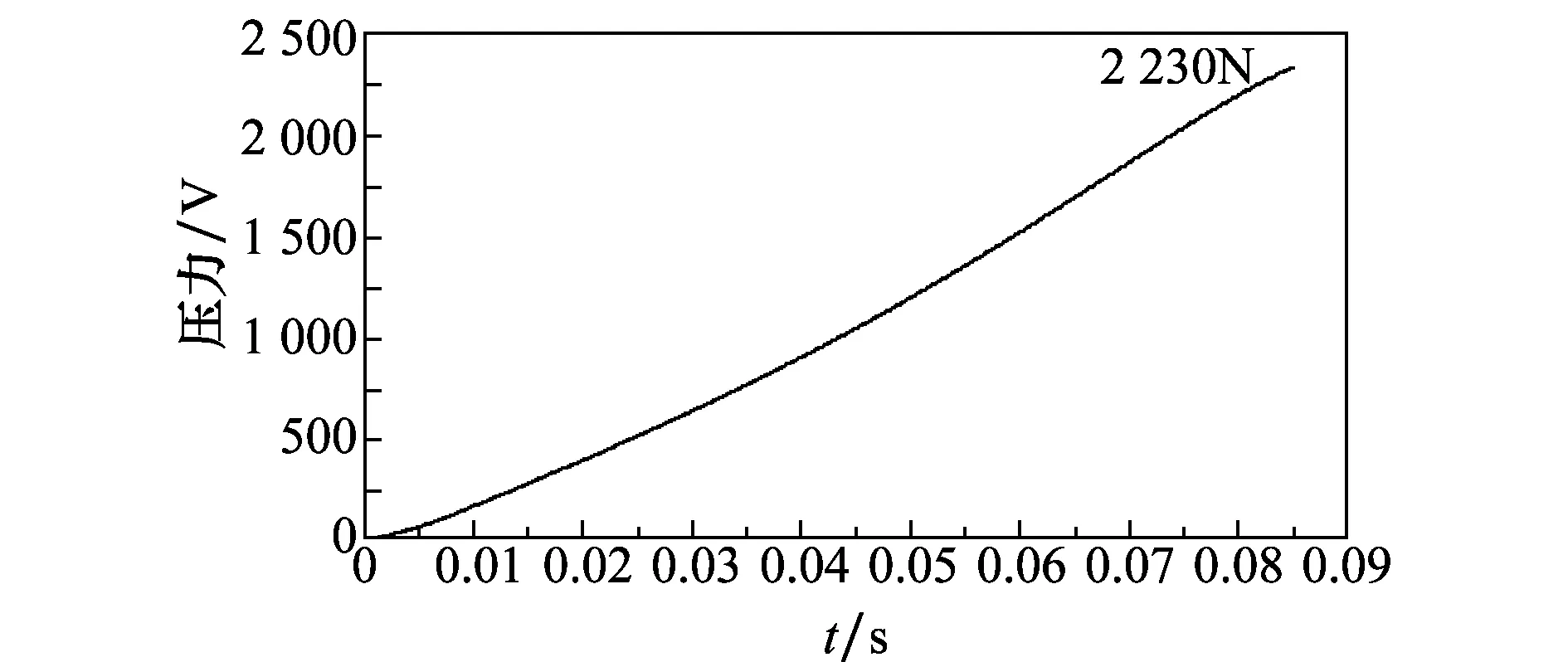
图6 导弹所受科氏力仿真曲线图Fig.6 Coriolis force on missile

2.3 载机大机动对发射分离参数影响分析

导弹弹射分离参数是衡量弹射发射装置最重要性能指标,直接影响到载机发射安全性和空空导弹初始弹道。弹射分离参数是指空空导弹相对于载机的相对运动参数。本文考虑了气动力和气动力矩对弹射分离参数的影响,考虑到弹射时间较短且为了初步研究大机动发射安全性,因此气动力和气动力矩暂假设为恒定值。事实上由于武器舱结构复杂,载机又做俯冲拉起机动发射,导弹发射时其气动流场相当复杂,需要进行CFD仿真计算并结合风洞试验进行专题研究。

图7为导弹弹射分离速度曲线,曲线终点为导弹与发射装置分离时刻点。如图:在载机无机动发射时(黑色实线),弹射分离速度为8.04 m/s,分离时间为110 ms;当考虑空中气动流场影响时,弹射分离速度会降低到7.93 m/s(C2曲线);当载机大机动发射时(C3和C4曲线),弹射分离速度为9.64 m/s,分离时间为90 ms。因此,离心力将增加导弹弹射分离速度,有利于发射安全性;科氏力对分离速度几乎不会产生影响。

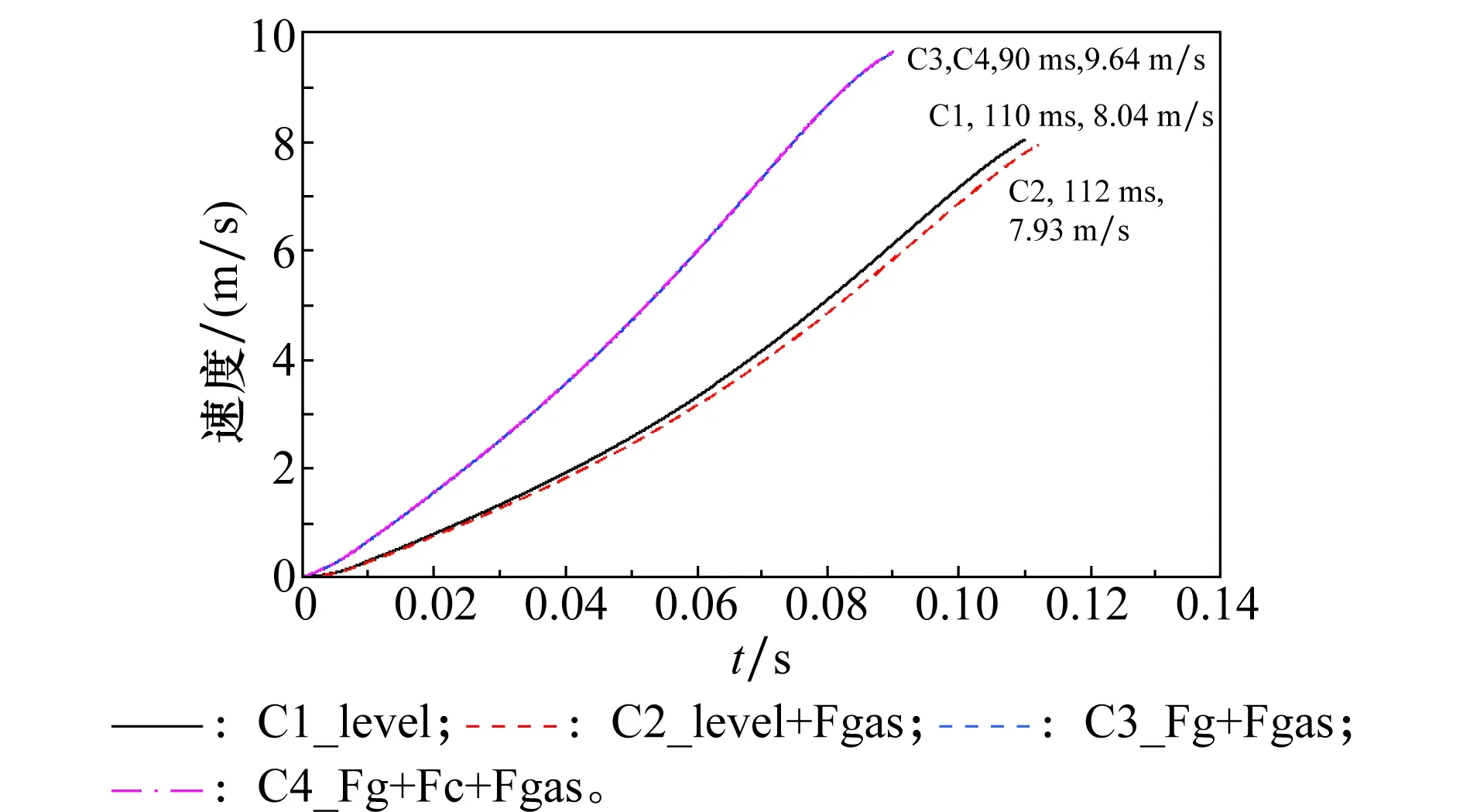
图7 导弹弹射分离速度曲线图Fig.7 Eject separation velocity of missile

图8为导弹弹射分离角速度曲线,曲线终点为导弹与发射装置分离时刻点。导弹发射时要求相对载机具有向下倾斜的低头角速度,以保证载机的安全。如图,在载机平飞无机动发射时,弹射分离低头角速度为32°/s(C1曲线);当考虑空中气动流场影响时,弹射分离角速度降低到29°/s(C2曲线);当只考虑高过载离心力时,弹射分离低头角速度为27.5°/s(C3曲线);当同时考虑高过载离心力和科氏力时,弹射分离低头角速度为30°/s(C4曲线)。可以看出,载机大机动发射时,导弹弹射分离角速度会出现小幅度的偏离,考虑到分离角速度安全范围是20°/s～50°/s,因此可以认为离心力和科氏力对导弹弹射分离角速度的影响较小,大机动发射时对导弹发射分离姿态影响不大。

3 大机动发射试验研究

采用试验验证战机准恒定离心过载俯冲拉起大机动发射时的相关发射动力学特性,包括发射装置相关受力情况。图9为载机俯冲拉起大机动弹射试验时发射装置与导弹的挂装接口的结构破坏图,从图中可以看出左右两挡块边缘均出现挤压变形和刮擦损伤。

在载机大机动发射时,由于导弹受到沿航向的科氏力作用,该科氏力将对发射装置的航向约束结构产生作用力,在导弹与发射装置逐渐脱离过程中,导弹吊挂与发射装置约束结构的接触面越来越小,直至最终呈“边缘-边缘”的线接触状态,在该状态下接触面的接触应力急剧增加,使发射装置和导弹的接触面产生强烈的挤压刮擦,导致结构破坏失效,威胁发射安全性。因此弹射发射装置在设计时应重视大机动发射时科氏力对结构强度的影响。