相对丰度匹配的网格级联分离多组分同位素混合物

应振根，曾 实

（1.衢州学院机械工程学院，浙江衢州 324000；2.清华大学工程物理系，北京 100084）

相对丰度匹配的网格级联分离多组分同位素混合物

应振根1，曾 实2

（1.衢州学院机械工程学院，浙江衢州 324000；2.清华大学工程物理系，北京 100084）

本文提出了一种仅两个取料的网格级联——相对丰度匹配的网格级联。其上半部分是理想网格级联，下半部分是有回流的网格级联。只要在回流点处某两种关键组分的分离是对称分离，这两种组分即能满足丰度无混合的条件。给出了相对丰度匹配网格级联的计算方法，并针对分离多组分同位素混合物的不同情况，对该种网格级联的分离性能进行了讨论。结果表明，相对丰度匹配网格级联能很好地实现同位素的分离，在级联总流量相同的情况下，能达到不亚于常规相对丰度匹配级联的分离效果。

同位素分离；相对丰度匹配；网格级联

在铀同位素分离中，获取高性能的分离级联是追求的目标，理想级联就是为此而提出的，其特征是各级均为对称分离，并且在级联的交汇点处，来流中组分的丰度无混合。不同稳定同位素的需求不断增大，而这些同位素大多是多组分同位素，为满足这些同位素的需求，多组分分离的研究成为一持久的课题。借鉴双组分分离理想级联的概念，设计开发了多种多组分分离级联，如丰度匹配级联［1－2］、准理想级联［35］、Q级联［6－7］等，但这些级联并不能实现在交汇点处来流中所有组分的丰度无混合。

文献［8］提出了网格级联的概念，研究发现，网格级联可能是一种能在交汇点实现所有组分丰度无混合的级联。文献［9-10］列出了获取网格级联的方式，并给出了理想网格级联的计算方法。只要给定任意两种组分在每级均是对称分离的条件，就可对各级的流量、丰度和分流比联立方程，求解出理想网格级联每级的流量、丰度和分流比。研究发现，理想网格级联在各级分流比按一定规律确定的情况下，能实现在交汇点处所有组分丰度无混合。

理想网格级联虽实现了在交汇点处所有组分丰度无混合，但它的最后一层无回流，具有多个取料，且层数越多，取料个数越多，这在实际应用中是不合适的。为使网格级联更实用，需减少级联的取料个数，将最后一层的多个出流回流至上一级或下一级的入口处，形成有回流的网格级联。本文将探讨一种特殊的有回流的网格级联——相对丰度匹配网格级联，给出该级联的计算方法，并对此级联的分离性能进行研究。

1 相对丰度匹配网格级联的概念

图1为理想网格级联。图中，每个方框代表1个分离器，入流为供料（F），左边的出流为贫料（W），右边的出流为精料（P）。

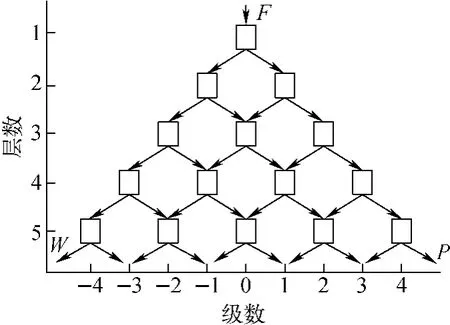
图1 理想网格级联Fig.1 Ideal net cascade

网格级联的分布有水平和垂直两个方向，如图1所示，不同水平位置处的分离器称为级，不同垂直位置处的分离器称为层。对于网格级联中的某分离器，用水平方向和垂直方向上的两个数字来描述它的位置，若它的位置在第l层的第s级，可称其为级（l，s），或第（l，s）级。

理想网格级联由于在级联的最后一层无回流，具有多个取料，在实际应用中是不合适的。更通用的方法是减小取料的个数，将最后一层的多余取料返回至上一级或下一级的入流，形成具有回流的网格级联。

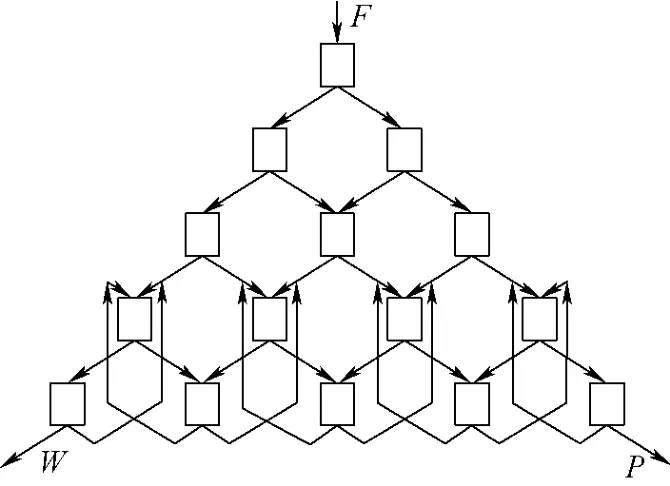
图2 同一层的取料回流的网格级联Fig.2 Net cascade with recirculation flows from same layer

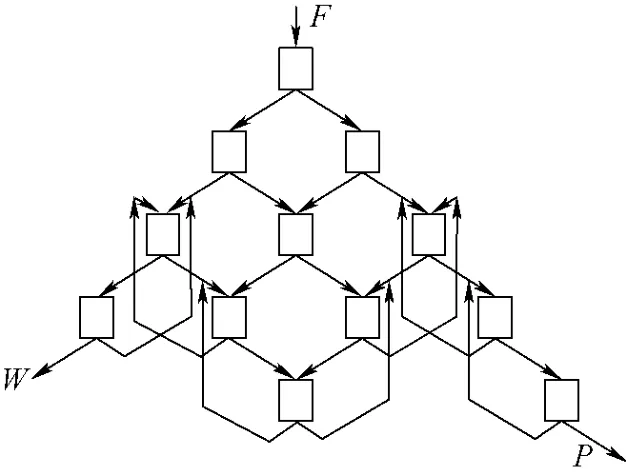
图3 不同层的取料回流的网格级联Fig.3 Net cascade with recirculation flows from different layers

图2、3是两种不同形式的有回流的网格级联。图2为最后一层的级数达饱和的情况，即最后的第L层含有L级，此时级联的最后一层仅P和W两处取料，其余所有级的精料和贫料均分别回流至倒数第2层的相应位置。图3为最后一层的级数不饱和的情况，即最后的第L层未达到L级，这时除最后一层相应的精料和贫料回流至倒数第2层外，倒数第2层未流入最后一层的精料或贫料分别回流至倒数第3层。

显然，有回流后，在回流点就不能保证所有组分丰度无混合。这时，可将网格级联分成上、下两个部分，以图2的网格级联为例，最顶上的3层是理想网格级联，共有1处供料、6处取料。而下方的第4、5两层可看成是有4处供料、2处取料、总级数为9的常规级联。为方便与常规级联比较，可将有回流的网格级联等效为一种只有级数变化的级联，即将网格级联中层数不同但级数相同的所有级均视为同一级，此时级联的级数从左向右顺序排列。图2的网格级联可等效为一总级数为9、供料位于第5级、取料位于两端的级联（图4）。

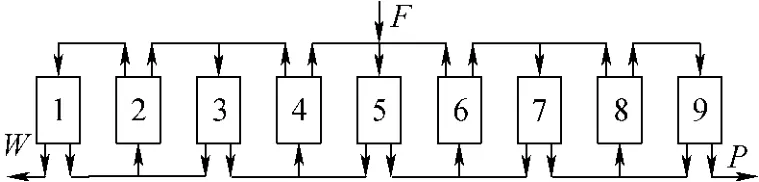
图4 有回流的网格级联的等效级联Fig.4 Equivalent cascade of net cascade with recirculation flows

此时，网格级联所有级数s相同但层数l不同的级视为等效级联的一级，各级的流量由下式计算：

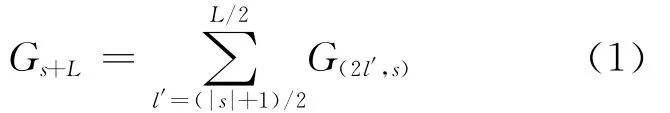
虽然有回流的网格级联并不能保证在回流点处所有组分均无丰度混合，但通过对分流比、分离系数、流量等参数的特殊设置，可使网格级联满足某些具体的分离需求。在这里，借鉴相对丰度匹配级联的概念，设定网格级联下半部分（即有回流的部分）为相对丰度匹配级联，上半部分仍为理想网格级联，那么这样的网格级联就称为相对丰度匹配的网格级联。相对丰度匹配网格级联的特征是在回流点处所有来流中某两种关键组分的分离均是对称分离。如取第i组分和第j组分为关键组分，那么在相对丰度匹配网格级联的回流点处，这两种组分的分离系数αij、βij与全分离因子γij的关系满足：

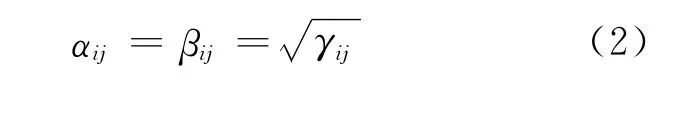
2 相对丰度匹配网格级联的确定

为确定相对丰度匹配网格级联的流量和分流比等参数，需对其进行相应的计算。根据相对丰度匹配网格级联的形状和结构，它的计算分为两个部分：上半部分仍按理想网格级联的方法进行计算；下半部分则可借鉴常规相对丰度匹配级联的计算方法。

设相对丰度匹配网格级联的总层数为L，分离的同位素混合物总组分数为NC，第k1、k2组分为关键组分，其分子量分别为Mk1、Mk2。级联各级的流量方程为：

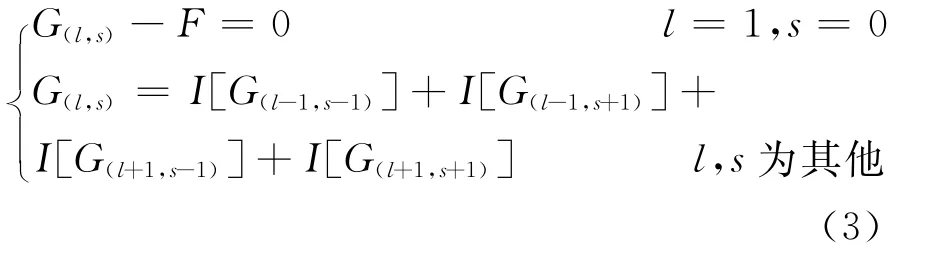
其中：

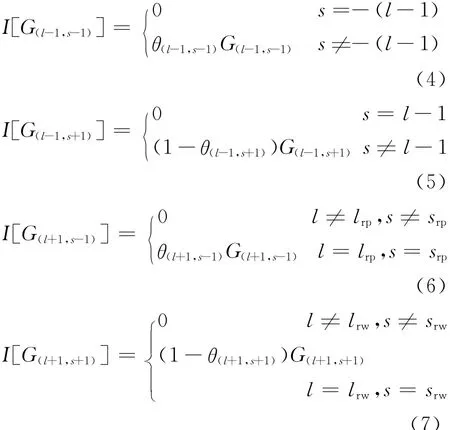
式中，第（lrp，srp）级和第（lrw，srw）级分别存在从下一层回流至该级的精料和贫料。

丰度方程为：

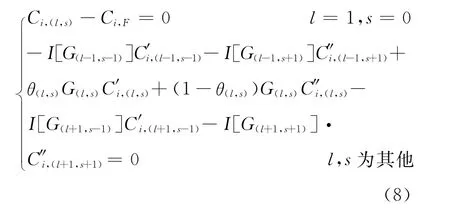
式（3）、（8）是关于流量、分流比θ和丰度C的非线性方程组，可采用迭代方法进行计算。

这里采用对流量G（l，s）进行迭代的计算方法，步骤如下：

1）求解结构和级数与相对丰度匹配网格级联完全相同的理想网格级联的情况，得到各级的流量、分流比及丰度分布。

2）利用第1步的结果，根据下述方程计算下半部分各级的供料丰度。

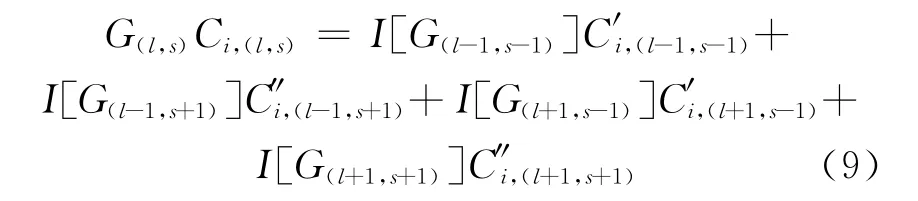
3）根据下述分流比和丰度方程组计算下半部分级联各级的分流比和丰度。i其中，γ0为基本全分离因子。

4）由式（3）重新计算下半部分各级的流量分布。

5）重复2～4步的过程，即对回流部分各级的流量、分流比和丰度分布进行多次迭代计算，直到满足迭代结束的准则：其中：上标m和m＋1为迭代次数；N为网格级联的总级数；ε为给定的小数，如可取ε＝10－8。

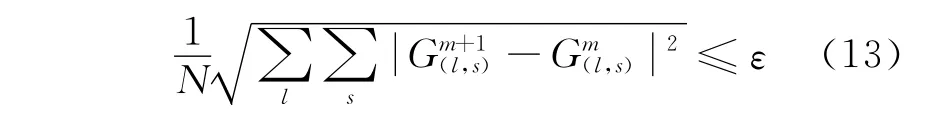
3 计算和讨论

以分离WF6同位素混合物为例，对相对丰度匹配网格级联的分离结果进行计算和讨论。WF6各组分的丰度列于表1。

网格级联共20层，其结构与图2类似，是最后一层级数饱和的相对丰度匹配网格级联。供料F＝1位于第（1，0）级，第（20，19）级的精料和第（20，－19）级的贫料作为级联的精料和贫料取料，第20层其余各级的精料和贫料都回流到第19层的相应位置，各级离心机的基本全分离因子γ0＝1.078。分别对以第2、3组分和第3、4组分为关键组分的两种情况对相对丰度匹配网格级联进行计算和讨论。

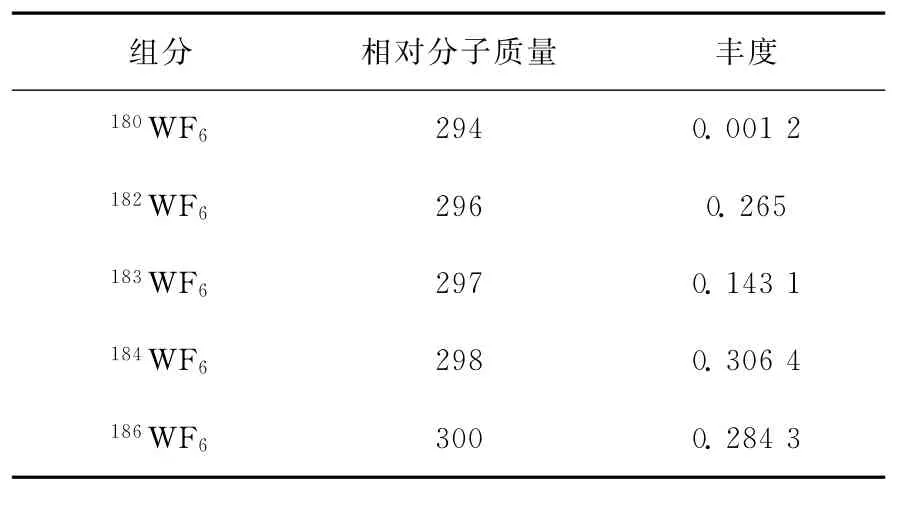
表1 WF6混合物的组分的丰度Table 1 Concentrations of components for WF6mixture

表2 相对丰度匹配网格级联各交汇点的来流丰度（k1＝2，k2＝3）Table 2 Concentrations at confluent points in matched abundance ratio net cascade（k1＝2，k2＝3）

表2、3分别列出了上述两种情况下，网格级联第（19，2）级和第（20，5）级的来流丰度对比。其中，第（19，2）级共有4股来流，分别是第（18，1）级的精料、第（18，3）级的贫料、第（20，1）级的精料及第（20，3）级的贫料。第（20，5）级共有2股来流，分别是第（19，4）级的精料和第（19，6）级的贫料。从表2可知，在回流部分的交汇点处，除第18层的两股来流外，同位素混合物各组分在各股来流中的丰度均不相同，但第（19，2）级和第（20，5）级的各股来流中两种关键组分的相对丰度却分别相等。从表3中可得出相同的结论。

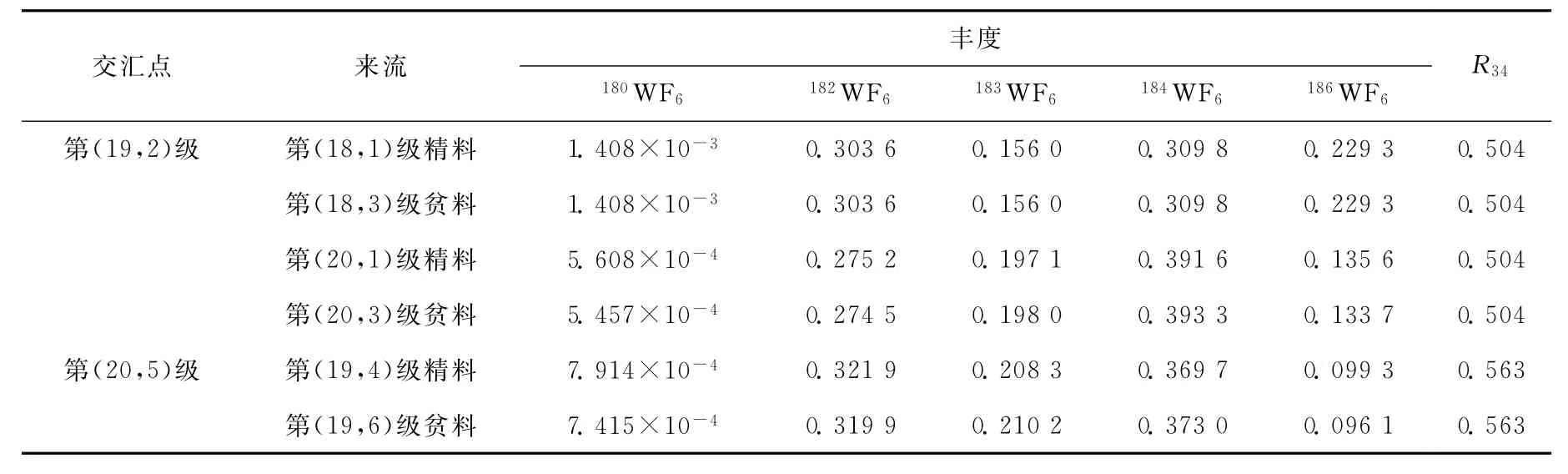
表3 相对丰度匹配网格级联各交汇点的来流丰度（k1＝3，k2＝4）Table 3 Concentrations at confluent points in matched abundance ratio net cascade（k1＝3，k2＝4）

更精细的结果显示，第k1和第k2两种关键组分的分离系数αk1k2、βk1k2在各级均分别相等。这两种关键组分的相对丰度在交汇处的各来流中相等，它们的数值满足：

但其他组分的相对丰度却不满足上式。

图5为以第2和第3组分为关键组分，相对丰度匹配网格级联不同层的分流比分布情况。可见，各层的分流比均在0.5附近，每层级联的分流比均随级数从左到右逐级递增，这是由于在级联中轻组分向右端聚集，重组分向左端聚集，各级的分流比逐级变化以减少丰度的混合。从图5还可看出，第19、20两层的分流比很接近，第17、18两层的分流比也非常接近，但它们之间分流比的差值却较明显。这是因为第19、20两层是有回流的部分，而第17、18两层是理想网格级联的部分，第19、20两层各级的入流情况较第17、18两层的情况复杂，因此其各级的分流比不同于第17、18两层的分流比，以适应在有回流的情况下对同位素混合物的分离。

图5 不同层的各级分流比分布Fig.5 Split ratio distributions on different layers

图6为不同层的各级流量分布。从图可见，相对丰度匹配网格级联的每层均是中间级的流量最大，且流量向左右两边逐级递减，这与理想网格级联的流量分布情况相似。由于第19层存在从第20层回流的流量，因此，第19、20两层的流量较第17、18两层的流量大，从图可看出，前者比后者大1～2个数量级。

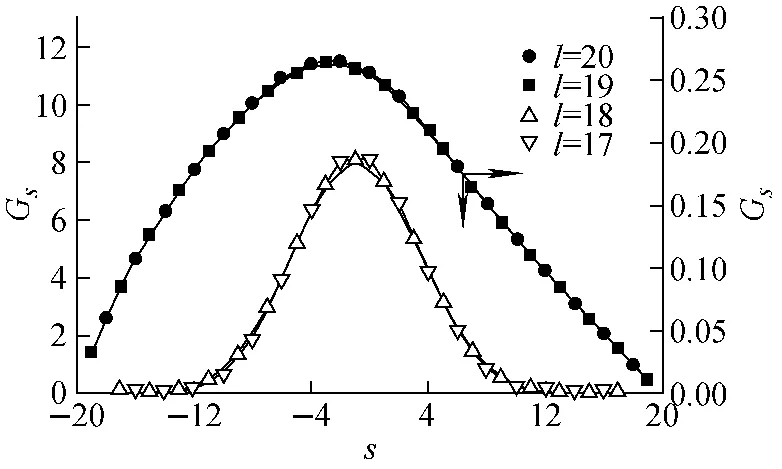
图6 不同层的各级流量分布Fig.6 Flow distributions on different layers

图7为WF6混合物的5种组分在相对丰度匹配网格级联不同层的精料丰度分布情况。可见，丰度分布和级联的分流比分布有相同的趋势，即第19、20两层的丰度分布非常接近，第17、18两层的丰度分布也非常接近，但两者之间的差值较明显，这是由于相对丰度匹配网格级联的前18层是理想网格级联，而在第19层各级的进口处存在回流，导致丰度混合，使两部分的丰度分布有明显的差别。

但同位素组分的丰度分布在级联上、下两部分中变化趋势一致。从图7可看出，较轻组分180WF6和182WF6的丰度随级数的增加单调增大，而最重组分186WF6的丰度随着级数的增加单调减小。中间组分183WF6和184WF6的丰度则随着级数先增大后减小，在级联的中间某级达丰度的最大值。当然，由于级联上、下两部分存在因有无回流而产生的差异，中间组分丰度最大值所在的级数在两部分中并不相同。总体来说，在相对丰度匹配网格级联中，轻组分向级联的轻端聚集，重组分向级联的重端聚集，这和常规的相对丰度匹配级联的分离性能是相同的。

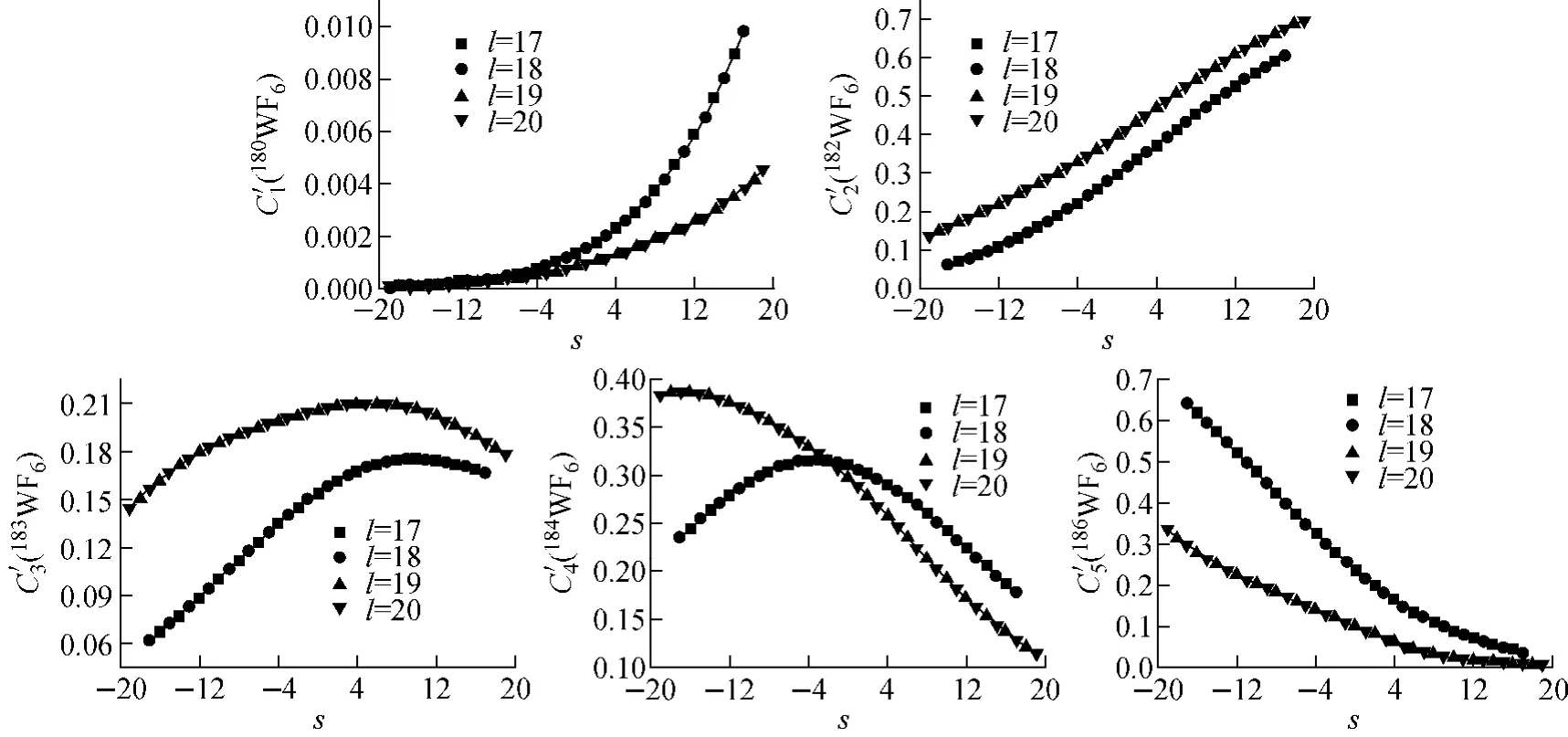
图7 各组分的丰度分布Fig.7 Concentration distributions of different components

表4 相对丰度匹配的网格级联和常规级联的精料Table 4 Product withdrawal of matched abundance ratio net cascade and conventional cascade

图8为根据式（2）的方法，将相对丰度匹配网格级联等效成级数从左向右顺序排列的级联后，网格级联与常规级联的流量分布，其中常规级联的数据根据文献［11］的方法计算。从图可见，两种级联的流量分布完全一致。表4、5为此时两种级联的精、贫料取料及其丰度的情况。从表可看出，在级联长度和供料位置相同的情况下，相对丰度匹配的网格级联与常规级联的精料取料、贫料取料均相等，且它们的丰度组成均分别相同。

这是由于网格级联最后一层各级的出流（除精、贫料取料外）均回流至上一层的入口，最后两层形成有回流的级联。在级联各回流处，由于并非来流中的所有组分丰度均相同，因此，在回流点处产生了较大的丰度混合，且抵消了其上半部分理想网格级联各组分均无丰度混合的效果，使其总体的分离性能与常规的相对丰度匹配级联一致，从而两种级联的流量分布相同，精、贫料取料的大小以及它们的丰度组成也相同。

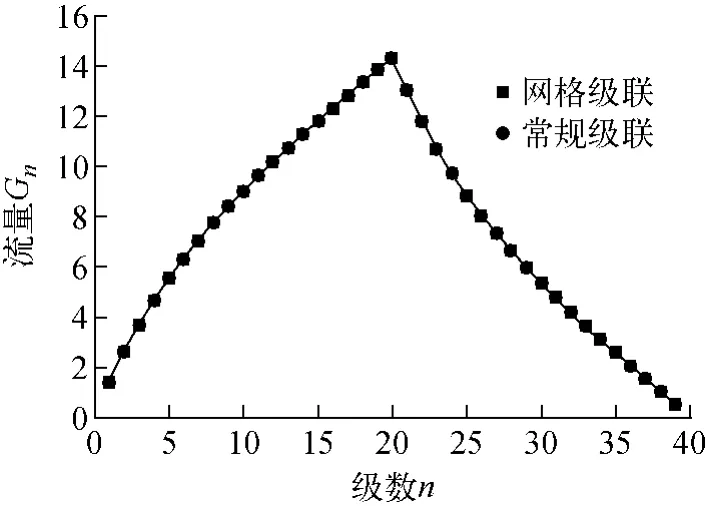
图8 相对丰度匹配的网格级联和常规级联的流量分布Fig.8 Flow distributions of matched abundance ratio net cascade and conventional cascade

表5 相对丰度匹配的网格级联和常规级联的贫料Table 5 Waste withdrawal of matched abundance ratio net cascade and conventional cascade

根据同样的方法，针对以第3、4组分为关键组分的情况，对相对丰度匹配的网格级联和常规级联的计算分析可得出相同的结论。

4 结论

为提高网格级联在实际使用过程中的适用性，本文提出了一种特殊的有回流的网格级联——相对丰度匹配网格级联。该级联仅两个取料，上半部分为理想网格级联，而下半部分则是有回流的网格级联。只要在回流点处满足某两种关键组分的分离是对称分离的条件，即能构成相对丰度匹配网格级联。

在相对丰度匹配的网格级联中，各级的分流比均约0.5，在每层中分流比均随着级数的增加逐渐增大，且有回流的部分与理想网格级联部分存在明显差距。各层的流量分布情况相似，只是由于最后两层存在回流，其流量较上部理想网格级联部分大很多。相对丰度匹配的网格级联能很好地实现多组分同位素混合物的分离，从整体性能看，在级联总流量相等的情况下，相对丰度匹配网格级联能达到不亚于常规相对丰度匹配级联的分离效果。

显然，网格级联看似较普通的双管道级联复杂很多，但网格级联独特的多组分分离时所有组分均无混合的性质如何利用值得探讨。本文为研究解决这些问题提供了一个思路。

［1］ de la GARZA A，GARRETT G A，MURPHY J E.Multicomponent isotope separation in cascades［J］.Chemical Engineering Science，1961，15：188-200.

［2］ de la GARZA A.A generalization of the matched abundance-ratio cascade for multicomponent isotope separation［J］.Chemical Engineering Science，1965，18：73-82.

［3］ APELBLAT A，ILAMED-LEHRER Y.The theory of a real isotope enriching cascade-Ⅰ［J］.Journal of Nuclear Energy，1968，22：1-14.

［4］ SAZYKIN A A.Quasi-ideal cascades for separation of multicomponent isotope mixtures［C］∥Proceeding of Conference on Physical and Chemical Processes in Selection of Atoms and Molecules.Zvenigorod：［s.n.］，2000：51-57.

［5］ SULABERIDZE G A，POTAPOV D V，BORISEVICH V D，et al.Special features of the enrichment of components with intermediate mass in a quasi-ideal cascade［J］.Atomic Energy，2006，100（1）：53-59.

［6］ KUCHEROV R Y，MINENKO V P.Theory of cascades for separating multi-component isotope mixtures［J］.Translated From Atomnaya Energiya，1965，19（4）：360-367.

［7］ KOLOKOL′TSOV N A，MINENKO V P，NIKOLAEV B I，et al.Design of cascades for separating isotope mixtures［J］.Translated From Atomnaya Energiya，1970，29（6）：425-429.

［8］ ZENG S，WANG L J，YING Z G，et al.Net cascade［C］∥Proceeding of 11th International Workshop on Separation Phenomena in Liquids and Gases.Petersburg，Russia：［s.n.］，2010.

［9］ 曾实，姜东君，应振根.一种完全无混合非常规同位素分离级联：网格级联［J］.中国核科学技术进展报告，2011，2：7-13.

ZENG Shi，JIANG Dongjun，YING Zhengen.A nonconventional isotope separation cascade without any mixing：Net cascade［J］.Progress Report on China Nuclear Science ＆Technology，2011，2：7-13（in Chinese）.

［10］ZENG S，YING Z G.A truly ideal cascade：Net cascade［J］.Separation Science and Technology，2012，47（7）：929-935.

［11］WOOD H G，BORISEVICH V D，SULABERIDZE G A.On a criterion efficiency for multi-isotope mixtures separation［J］.Separation Science and Technology，1999，34（3）：343-357.

Separation of Multi-component Isotope Mixtures by Matched Abundance Ratio Net Cascade

YING Zhen-gen1，ZENG Shi2
（1.College of Mechanical Engineering，Quzhou University，Quzhou324000，China；2.Department of Engineering Physics，Tsinghua University，Beijing100084，China）

A net cascade with two withdraws named as matched abundance ratio net cascade was proposed.The upper part is an ideal net cascade，and the lower part is a net cascade with recirculation.If the separation of two key components is symmetrical，their abundances will not mix at inflow points.The computation method of the matched abundance ratio net cascade was given，and the separation performance was discussed through separating multi-component isotope mixtures in different cases.The results show that the matched abundance ratio net cascade can separate mixtures well，and its separation performance is no less than conventional matched abundance ratio cascade in case of same total flows.

isotope separation；matched abundance ratio；net cascade

TL25.01

：A

：1000-6931（2015）01-0006-07

10.7538／yzk.2015.49.01.0006

2014-05-19；

2014-07-15

国家自然科学基金资助项目（10875069）

应振根（1982—），男，浙江遂昌人，讲师，博士，从事同位素分离、新能源利用研究