基于时频差的高阶强跟踪UKF算法

周恭谦, 杨露菁, 刘 忠

(海军工程大学电子工程学院, 湖北 武汉 430033)

0 引 言

目标跟踪是对目标位置和速度的实时估计与预测,其被广泛的应用于军事领域之中。基于有源系统的目标跟踪技术发展较为成熟,但在军事对抗中很容易被干扰从而导致跟踪失败,因此基于无源系统的目标跟踪技术受到了广泛的关注。在无源跟踪系统中,多观测站可以通过接收目标信号的到达时间差(time difference of arrival, TDOA)和到达频率差(frequency difference of arrival, FDOA)来完成对目标位置和速度的估计,由于TDOA和FDOA 构建的模型为非线性方程组,所以基于TDOA/FDOA的目标跟踪属于非线性滤波问题。

针对非线性滤波问题粒子滤波(particle filter, PF)[1-5]随机变量不要求高斯分布,估计精度较高受到广泛的关注,然而其计算复杂度较高,消耗时间过长。针对此文献[6]提出一种基于蝙蝠算法的粒子滤波(bat algorithm optimized particle filter, BA-PF),在原有算法引入飞行策略,降低了状态预测所需的粒子数量和提高了滤波的定位精度,但算法的复杂度仍然较高无法满足跟踪的实时性要求,而文献[7]提出一种交互式多模型(interactive multiple model, IMM)[8-10]与秩滤波(rank Kalman filter,RKF)[11]结合的算法在一定程度上提高了定位精度,但由于采用多个模型进行滤波并行和交互提好了计算复杂度,需要运行较长的时间。

无迹卡尔曼滤波(unscented Kalman filter, UKF)和容积卡尔曼滤波(cubature Kalman filter,CKF)作为新兴非线性滤波算法[12-16]被研究应用到多个领域,UKF算法的核心思想是通过无迹变换(unscented Transform, UT)去近似非线性系统状态的后验概率密度函数。而CKF的采用三阶球面-相径容积规则来近似非线性函数传递的后验均值和方差,归根到底其是UKF算法中UT变换的特殊形式[17]。为了提高CKF算法和UKF算法的估计精度:文献[18-19]提出了高阶球面-相径容积的采样方法来获取高于CKF阶数的估计精度。文献[20]提出一种正交容积卡尔曼滤波跟踪算法(orthogonal cubature Kalman filter,OCKF),通过引入一个特定的正交矩阵改进容积采样方法来减小标准容积采样方法的舍弃误差。文献[21]提出一种高斯和高阶无迹卡尔曼滤波算法,针对UKF提出了一种高阶无迹变换来提高非线性变换的近似精度。尽管这些算法一定程度上提高了UKF和CKF算法的估计精度,但当目标运动状态发生突变时 UKF和CKF算法出现的状态估计精度急剧下降的问题却无法解决。而强跟踪滤波(strong tracking filter, STF)[22-23]的引入能够解决UKF和CKF算法的鲁棒性问题,强跟踪滤波通过将次优渐消因子引入预测协方差阵,实时调整卡尔曼增益矩阵来保持对目标突变时良好的跟踪能力。近年来出现了很多STF结合UKF和CKF形成的新型的非线性滤波方法:基于新息正交原理的抗差UKF[24],基于多渐消因子强跟踪UKF[25-26],自适应高阶容积卡尔曼滤波(adaptive high-degree cubature Kalman filter, AHCKF)[27]。但这些算法需要进行在原算法的基础上增加了一次UT变换,提高了计算的复杂度,且对跟踪的估计精度提高有限。为了在不增加算法复杂度的情况下,提高算法对目标跟踪的精度和对突变的适应能力,本文提出一种高阶强跟踪卡尔曼滤波方法(high order strong tracking UKF, HSUKF):首先利用高斯概率密度函数高阶导数的极值作为Sigma样点进行UT转换,通过样本点捕捉更高阶的中心矩来提高非线性变换近似精度。然后将改进的STF算法引入到HUKF中在不增加计算复杂度的情况下进一步提高了算法的鲁棒性,通过仿真与UKF、OCKF、AHCKF、BA-PF以及IMM-RKF对比表明了该算法在状态突变时有更高的估计性能,最后通过实例论证了算法的有效性。

1 基于概率密度高阶无迹卡尔曼滤波

1.1 基于概率密度高阶导的UT转换

UT 变换作为一种计算随机变量经过非线性变换后统计特性的方法, 它通过设置Sigma 样点分布和权值来逼近样本非线性变换参量的矩[26]。事实上为了更好的近似随机变量经过非线性变换后的统计特性,Sigma点集应尽可能近似更高阶数的中心矩[28-29]。由于多维高斯变量的问题都可以转化为多个独立一维标准高斯分布的问题,下面先对服从一维标准高斯分布的随机变量x进行讨论,h(x)表示关于x的非线性函数,h(x)的期望可表示为

(1)

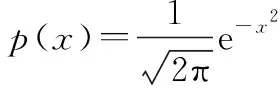
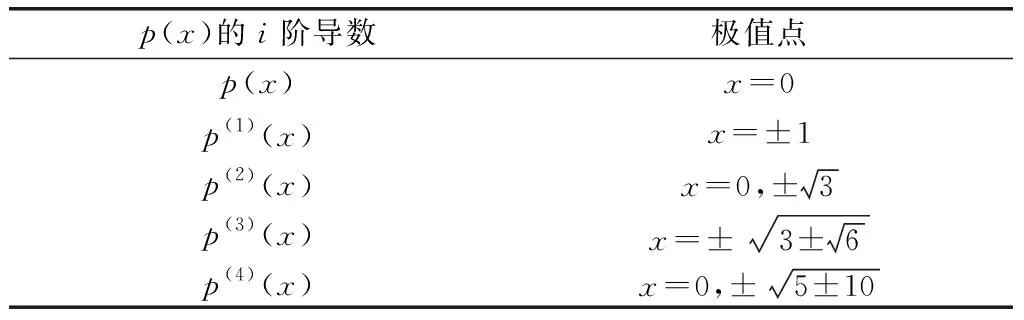
表1 p(x)各阶导数对应的极值点

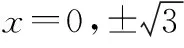
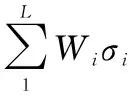
(2)

式中,[k]x表示x的高阶中心距。

定理1如果变量x服从均值为μ、方差为σ2的高斯分布,[k]x可以由μ和σ表示

(3)

则服从标准正态分布的x的高阶中心距为(k-1)!=1·3·5…(k-1)

综合式(2)、式(3)考虑sigma点对称分布的特性可得到矩阵方程式(4)：

(4)

将σi代入式(4)即可求得对应的Wi的值,则服从一维标准高斯分布的x的sigma点集Si为

Si={(0,W0),(±σ1,W1),…,(±σL,WL)}

(5)

将一维标准正态分布拓展到n维随机变量x中则有

(6)

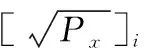
1.2 基于高斯密度高阶导的UKF

对离散的非线性系统

(7)

式中,Xk,Zk表示系统k时刻的状态向量和量测向量;f(·)、h(·)表示对应的转换函数;wk、vk为互不相关的高斯白噪声满足:

(8)

式中,Qk为非负定矩阵;Rk为正定矩阵,δkj为Kronecker-δ函数。

初始化

(9)

Sigma点计算

(10)

步骤1时间更新

将Sigma点进行非线性变换

εi,k|k-1=f(εi,k-1)

(11)

计算预测估计值

(12)

计算预测协方差

(13)

步骤2量测更新

(14)

非线性变换sigma点

(15)

计算预测测量值

(16)

预测新息协方差

(17)

预测互协方差矩阵

(18)

计算Kalman增益

(19)

更新误差协方差

(20)

更新状态

(21)

2 高阶强跟踪卡尔曼滤波

2.1 改进的强跟踪算法

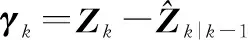
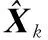
(22)

强跟踪UKF[22-24]通过将渐消因子λk引入预测协方差阵Pk|k-1,来对滤波增益矩阵Kk进行实时调整以提高系统的鲁棒性与自适应能力,具体为

(23)

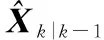
综上所述,强跟踪UKF算法在每次滤波过程中对比UKF都要多进行一次无迹变换,而这将会大大增加算法复杂度,不利于工程实践。当非线性系统中状态变量或者观测变量维数较高时,这个问题将会更加突出。

而根据式(19)可知调整Kalman增益还可通过调整Pxz,k|k-1,Pzz,k|k-1来实现,可将λk分别引入Pxz,k|k-1,Pzz,k|k-1中有

(24)

(25)

而将λk引入式(24)、式(25),则无需重新求解Pxz,k|k-1,Pzz,k|k-1,只需要两次UT变换就能实现滤波过程,而且新方法可以同时控制预测新息协方差和预测互协方差,比将λk引入Pk|k-1具有更强的自适应性。将式(24)、式(25)对式(17)、式(18)替换即是完整的高阶强跟踪卡尔曼滤波过程。

2.2 渐消因子的计算

式(24)、式(25)中渐消因子的计算可由式(26)计算得到

(26)

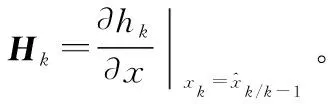
记HUKF的预测误差与估计误差分别为

(27)

(28)

引入未知对角阵βk使得

(29)

结合式(1)、式(22)、式(26)、式(29)有

(30)

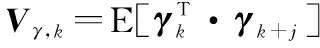
由式(30)可知

Pxz,k|k-1-KkVγ,k=0

(31)

结合式(19)、式(31)有

Kk(Pzz,k|k-1-Vγ,k)=0

(32)

结合式(17)、式(32)有

(33)

对(33)求解

(34)

式(34)的解λk可能小于1,为避免这种情况出现,最终渐消因子可定义为

(35)

式(34)中Vγ,k可由式(36)计算：

(36)

式中,0<ρ≤1为遗忘因子,通常选取为0.95。

3 实 验

3.1 多站TDOA/FDOA跟踪模型

第i个接收站到待测目标的距离可表示为

(37)

式中,‖·‖为求2范数运算。

待测目标到接收站i与到第一个接收站的距离差观测量可表示为

(38)

对式(37)求导可得距离关于时间的微分方程

(39)

对式(38)求导可得距离差关于时间的微分方程

(40)

频差观测量可表示为

(41)

式中,f0目标信号频率。

由上述可知基于TDOA/FDOA定位的状态方程可表示为

(42)

式中,wk-1为高斯白噪声,代表方差为σk-1的对角矩阵;φk为状态转移矩阵;T为观测时间间隔。

TDOA/FDOA定位测量方程可表示为

(43)

3.2 仿真实验

4个观测站的位置及速度如表2所示。

表2 接收站和目标的位置和速度

令目标做转弯运动,运动轨迹如图1所示[19,30],目标运动的起点为I,终点为F。

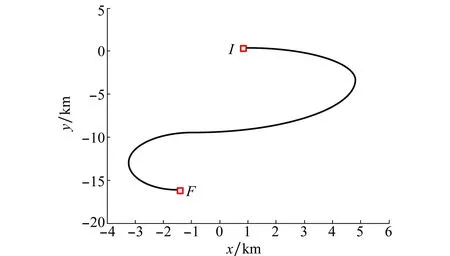
图1 目标运动轨迹示意图Fig.1 Sketch map of target motion

信号频率f0=3×108Hz,状态转移矩阵φk为

(44)

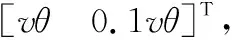
(45)

(46)

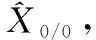
(47)

按照所给的参数进行仿真实验,图2和图3为本文提出的HSUKF算法和UKF、AHCKF、OCKF算法、BA-PF以及IMM-RKF位置跟踪RMSE和速度跟踪RMSE曲线。表3给出的是几种算法滤波过程中计算的采样点数、200次蒙特卡罗实验消耗的时间以及平均RMSE和速度RMSE的值。

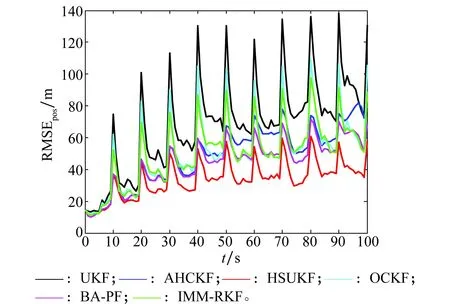
图2 位置跟踪RMSE曲线Fig.2 RMSE curve of Position tracking

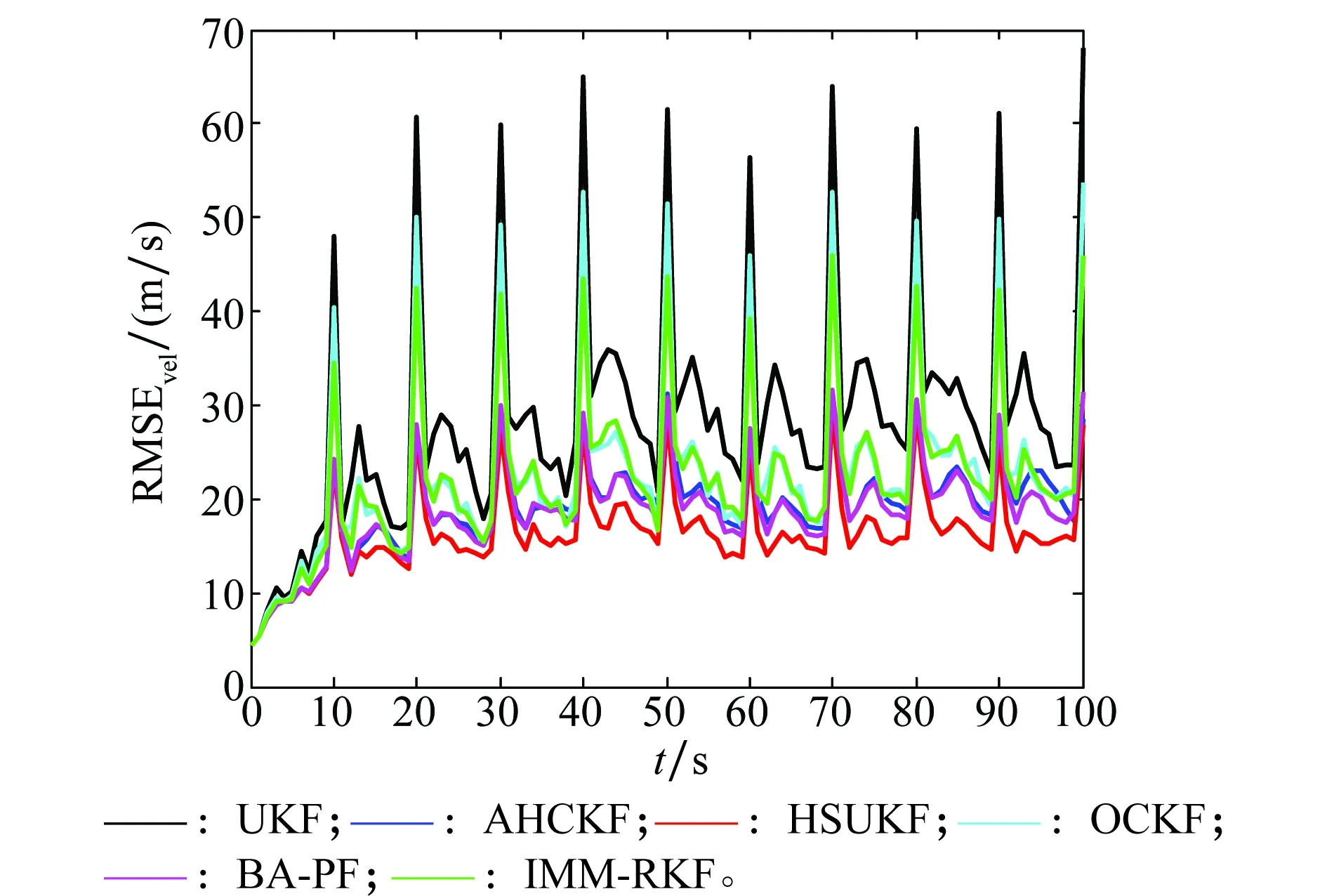
图3 速度跟踪RMSE曲线Fig.3 RMSE curve of velocity tracking

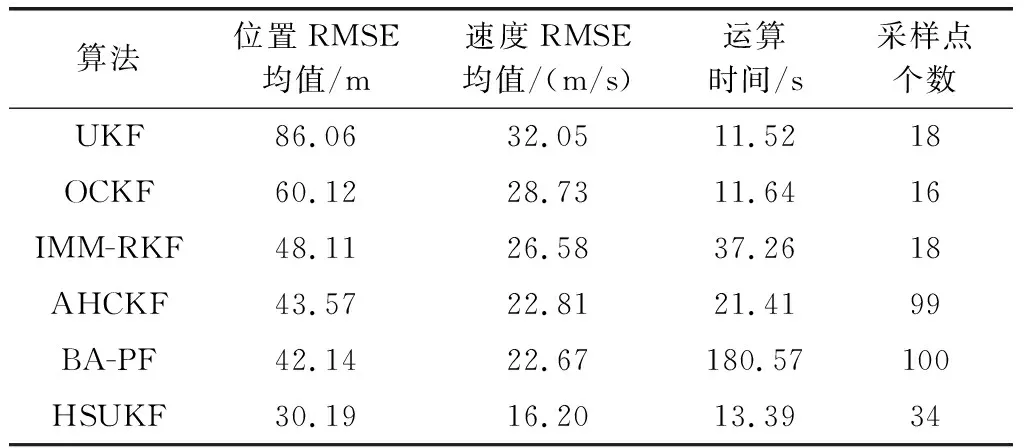
算法位置RMSE均值/m速度RMSE均值/(m/s)运算时间/s采样点个数UKF86.0632.0511.5218OCKF60.1228.7311.6416IMM-RKF48.1126.5837.2618AHCKF43.5722.8121.4199BA-PF42.1422.67180.57100HSUKF30.1916.2013.3934

从图2、图3可以看出在整个跟踪阶段HSUKF算法在跟踪过程中相对其他滤波算法RMSE最小, 这是因为HSUKF算法通过sigma点的选取近似非线性变换的8阶中心矩比其他算法获得了更高的精度,而BA-PF由于机动增量的引入增加了定位误差,仍保持着较高的定位精度,AHCKF提出了一种高阶球面-相径容积规则采样能近似5阶中心矩精度其定位精度仅次于HSUKF和BA-PF。OCKF通过引入一个特定的正交矩阵改进容积采样方法来使舍弃误差更小但其归根到底还是三阶滤波算法因而跟踪精度只比UKF算法高。当对目标进行加强机动后,UKF、OCKF以及IMM-RKF位置和速度RMSE迅速增大,且收敛较为缓慢,原因在于当目标状态突变时,系统模型不能正确的描述目标的真实运动,而依然根据模型进行状态更新会产生较大误差。而HSUKF算法和AHCKF的RMSE增大幅度远远小于上述3种方法,且滤波收敛速度均比上述2种方法快,说明HSUKF算法和AHCKF对于状态突变具有较强的跟踪能力。这是因为当目标状态突变时,强跟踪算法的引入能够充分提取残差序列中的有效信息,使输出的残差序列正交,通过渐消因子λk的引入实时调整增益矩阵Kk,从而明显的提高了跟踪精度。

从表3可以看出,HSUKF算法的位置RMSE均值和速度RMSE均值最小,进一步证明了算法的最优性。BA-PF算法虽然有着较高的定位精度,且BA-PF较传统PF算法降低了状态预测所需的粒子数目,但计算复杂度仍较高消耗时间最长。IMM-RKF消耗时间仅次于BA-PF算法这是由于采用多个模型进行滤波并行和交互从而增加了计算量。而其他4种算法的运算时间的长短与4种算法滤波过程中计算的采样点个数相关,由于UKF进行两次无迹变换,而一次无迹变换sigma采样点的数目为2n+1(n为状态向量的维数本文取4),由此计算滤波过程中UKF采样点总数为18,相对其他算法复杂度最低,因此运算时间最短,而OCKF算法只在CKF采样过程中引入了正交矩阵,并没有增加额外的计算量,,由于OCKF算法一次无迹变换sigma采样点的数目为2n,计算出OCKF算法的采样点总数为16,因此消耗的时间和UKF几乎相同。而AHCKF算法进行一次无迹变换采样点个数为2n2+1,而强跟踪算法的引入需经历3次无迹变换,所以AHCKF算法总的采样点个数为99,尽管AHCKF定位精度和适应状态突变能力有所增强,但算法复杂度明显提高,运算的时间也大大增加。而HSUKF算法一次无迹变换sigma采样点数为4n+1,而改进强跟踪算法引入只需两次无迹变换,因此HSUKF算法总的采样点个数为34,算法复杂度相对AHCKF大大的降低。而通过运行时间的对比HSUKF算法平均运行一次的时间相对于UKF来说只增加了0.01 s,证明了HSUKF算法能够兼顾计算复杂度和跟踪精度。

3.3 实例论证

为对运动目标的跟踪效果进行验证,在太平寺机场开展了低速动态试验,在一个小型航模飞机挂载UWB标签,如图4和图5所示。以观测区圆心为原点,3个定位基站按照(-50 m,0 m),(50 m,0 m),(0 m,-50 m)的正三角结构进行布设如图6所示。此外布设一套GPS-RTK高精度定位系统,作为系统实验结果的真值。低速动态试验主要开展了两大类型的飞行试验,第一类为定向接近试验,航模飞机携带UWB标签从左前方上由远到近接近定位基站,第二类为盘旋飞行试验。

图4 航模飞机Fig.4 Aircraft model aircraft

图5 安装于航模底部的UWB标签Fig.5 UWB label installed at the bottom of the model aircraft

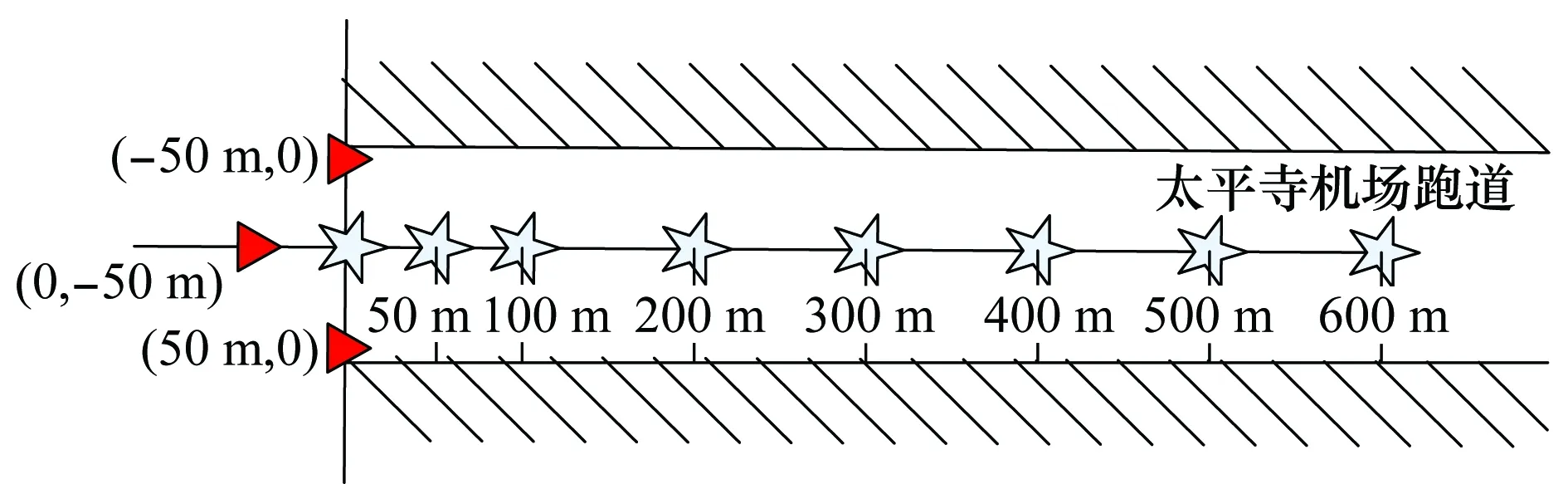
图6 基站布设示意图Fig.6 Schematic map of the base station

(1) 飞机左前方飞行

飞机从左前方方位角约为-14°的角度由远到近驶入,飞行的飞行态势如图7所示,使用HSUKF算法和GPS辅助跟踪定位曲线图如图8所示,由于飞机航模由人操作,在没有参照物情况下,飞行轨迹很难保持直线,状态容易发生由于突变,正好检验算法对突变情况的适应能力,从图8可以看出HSUKF算法在状态发生突变时也能保持良好的跟踪效果。

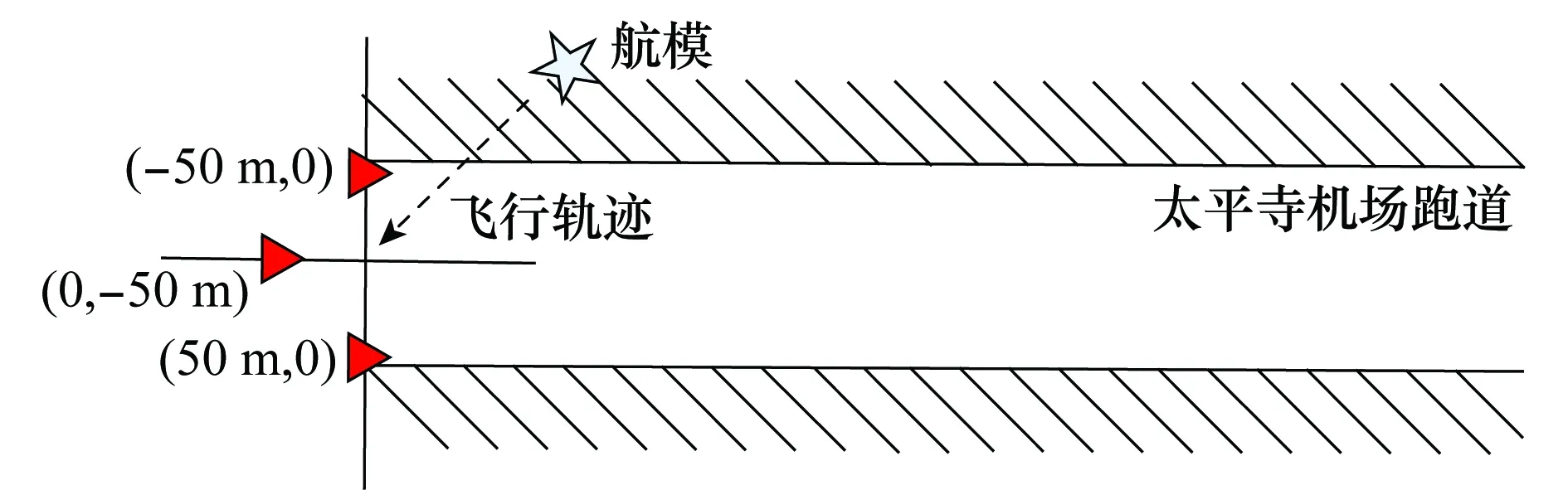
图7 左前方飞行示意图Fig.7 Schematic of left front flight

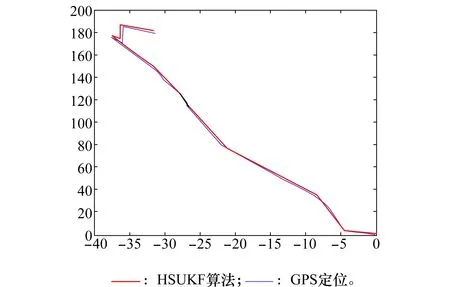
图8 HSUKF左前方飞行跟踪示意图Fig.8 HSUKF left forward flight tracking diagram

(2) 300 m处盘旋飞行

为了进一步论证目标进行曲线运动时的跟踪性能在距原点300 m距离上进行了顺时针盘旋飞行试验,盘旋飞行试验态势图如图9所示,使用HSUKF算法和GPS对目标进行跟踪,跟踪曲线如图10所示,由图10可知算法在目标进行曲线运动时也能够保持好的跟踪性能,在整个过程中目标状态发生了多个突变,HSUKF算法都能保持跟踪性能,进一步验证了本文算法的有效性。

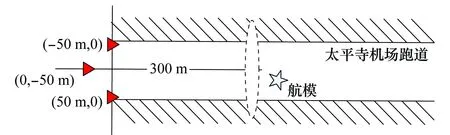
图9 盘旋飞行示意图Fig.9 Schematic diagram of circling flight

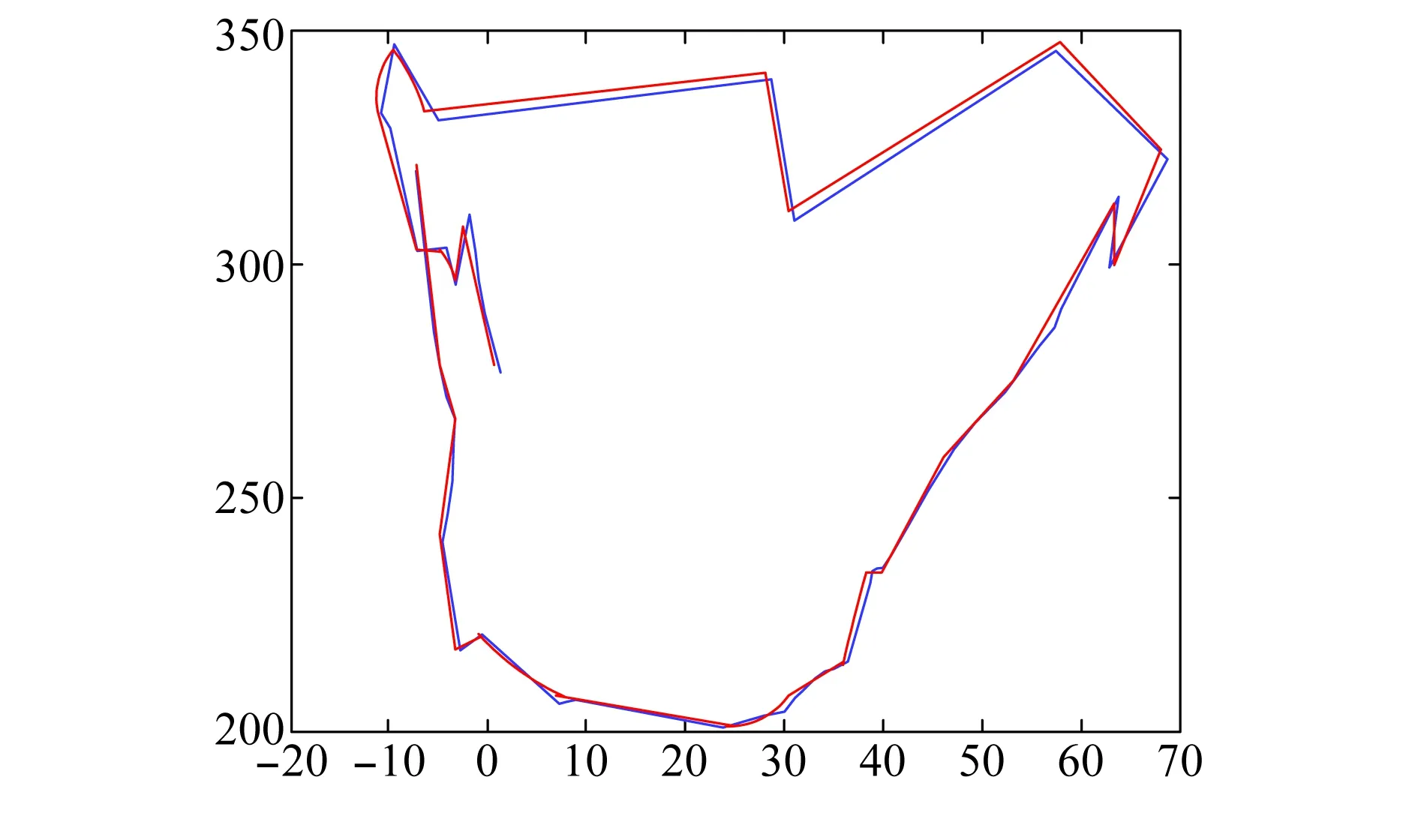
图10 HSUKF盘旋飞行跟踪示意图Fig.10 HSUKF circling flight tracking diagram

4 结 论

本文提出了HSUKF算法解决UKF在系统状态发生突变时估计精度下降的问题。通过将改进的STF算法与基于概率密度的HUKF算法相结合,在不增加计算复杂度的情况下,提高了定位精度和鲁棒性。通过将HSUKF和UKF、OCKF以及AHCKF对比证明了本文算法的最优性,最后通过实例验证了HSUKF算法的有效性。