处理冲突证据的一致性组合规则

李鸿飞, 王靳然, 敬忠良

(1. 上海交通大学航空航天学院, 上海 200240; 2. 中国人民解放军95174部队, 湖北 武汉 430040)

0 引 言

随着网络通信技术、传感器技术和信息处理技术的全面发展,以及无人机集群、车联网等场景需求的迅速增长,分布式融合已成为信息融合领域的一个研究热点。与集中式融合单一融合节点结构不同,分布式融合存在多个融合节点,各融合节点信息需要有较高的一致性。Dempster-Shafer (DS)理论以其在不确定性的表示和组合方面的优势在空中目标识别、车联网等信息融合领域得到了广泛的应用[1-3],而DS理论组合规则组合结果的一致性程度,尤其高冲突证据情况下的一致性,是DS理论在分布式融合系统中应用的基础。

DS理论是由Dempster提出[4]并由Shafer完善和扩展[5],其核心是Dempster组合规则。如何解决Dempster组合规则在处理高冲突证据时的悖论问题,一直是证据理论组合规则研究的重点,国内外学者主要主要从3个方面进行研究。①组合规则的修正。认为悖论问题源于冲突分配的不合理,应对冲突分配进行改进。如Yager组合规则[6]、Smets组合规则[7]、孙全组合规则[8]、Murphy组合规则[9],以及各种基于冲突分配策略的组合规则等。②证据的修正。认为问题在于Dempster组合规则假设每个证据源完全可信,但是实际上原始证据源的可信度和重要性通常是有差别的,需要预处理证据源。如预处理证据后再应用Dempster组合规则[10-11];通过度量证据冲突,确定折扣因子修正证据源,此外,一些研究融合了这两方面内容[12],分析了冲突原因[13]。③辨识框架的修正。有学者认为要求焦元互斥在很多情况下与已有认知存在冲突,应对DS理论的互斥要求进行修正,提出了Dezert Smarandache (DSm)理论[14],重新构建了新的理论体系,典型的组合规则有混合DSm组合规则[15]、比例冲突再分配(proportional conflict redistribution, PCR)组合规则[16]等,最近还有学者从辨识框架不完整角度解释和研究冲突信息处理[17-18]。

对组合规则的各种改进使基于原始证据和Dempster组合规则的融合结构发生了变化,一些Dempster组合规则具有的良好性质也发生了变化,如证据组合的结合性。结合性是Dempster提出Dmepster组合规则时指出组合规则应具备的基本性质之一[1]。Yager指出结合性是一种要求很高的性质[19],由于改进方法对Dempster组合规则“同权扩大”冲突分配方法的改变,使绝大部分改进无法满足结合性,Yager提出对组合规则进行线性变换,通过焦元映射得到准结合性,但这种方法无法处理焦元关系复杂的情况。Cattaneo[20]对非独立证据组合时的结合性进行了分析,但没有给出有效的组合规则。Daniel对冲突和结合性的关系进行分析,提出了最小矛盾(minimal contradictions,minC)组合规则[21],是Shafer模型下结合性研究比较深入的文献,但由于Shafer模型辨识框架互斥的限制使Daniel提出冲突表示和冲突分配是两个独立的系统,冲突理解和处理带来了很大困难,这也说明了传统的Shafer模型难以克服冲突精确表示的难题。Dezert在文献[16]说明了PCR规则也不满足结合性,针对证据顺序问题,冲突的保留是解决结合性问题的有效途径,但没有给出具体实现的组合规则。

从上述分析可知,当冲突处理方式改进时组合规则结合性难以保持,因此组合结果一致性可以衡量证据顺序动态变化时组合规则的有效性。本文首先对组合规则一致性进行了分析,然后基于自由Dezert Smarandache(DSm)模型实现对冲突信度的保留,在此基础上提出一种新的一致性组合规则,依据保留先前冲突信度,通过先前冲突信度及当前证据生成权重,并基于所获得权重对先前冲突信度和当前冲突信度进行分配完成证据组合。

1 组合规则一致性分析

1.1 组合规则的结合性

结合性是组合规则的基本性质之一。Dempster在文献[1]提出了组合规则的结合性:当有多条证据进行合成时,证据的顺序不影响证据的合成结果。即存在m1(·),m2(·),m3(·),辨识框架为GΘa[0,1],当存在A∈GΘ,有((m1⊕m2)⊕m3)(A)=(m1⊕(m2⊕m3))(A),则组合规则⊕具有结合性。

1.2 组合规则的一致性

结合性对组合规则要求过强,大部分改进规则无法满足。组合规则不满足结合性无法表示证据顺序动态变化时组合结果的不一致程度。因此,组合结果的相似程度可以衡量组合规则的一致性,一致性的度量值称为一致度。在众多证据一致度度量方法中,基于距离的一致度确定方法由于其物理意义明确、计算步骤简洁、冲突判定准确在证据融合中广泛应用。本文采用文献[22]方法,基于证据之间的支持度得到证据的一致度。该度量方法的处理过程分为4个步骤。

假设有N个融合节点,每个节点得到顺序不同的N个组合结果mk(k=1,2,…,N),Θ为辨识框架,mi和mj是组合结果中的两个基本信度分配,以向量的形式表示为mi、mj。

步骤1计算证据间的距离

(1)

(2)

式中,G(A,B)的确定采用文献[20]的基数确定方法。

步骤2计算证据间的相似度

sim(mi,mj)=1-dUJ(mi,mj)

(3)

步骤3计算证据的支持度及可信度

(4)

(5)

步骤4计算证据的一致度

(6)

2 基于自由DSm模型的冲突保留

2.1 DSm模型

Dempster规则对信度函数进行合成时,分为合成信度和冲突信度(全局冲突),再将合成信度归一化得到组合结果。合成信度满足乘性规则,因此归一化后的组合结果仍然满足结合性。但Dempster组合规则在处理冲突证据时存在悖论问题,这促使了各种改进规则的出现,改进规则对冲突的分配根据各种权重而定,而不再是比例归一化,造成了组合规则一致性的差异。传统的Shafer模型没有冲突焦元的表示形式,处理焦元间的复杂组合关系时,将不同焦元间的冲突均作为冲突信度一体看待,难以对焦元进行精细处理。2003年,Dezert和Smarandache提出了DSm理论,DSm理论中加入了冲突焦元,不再要求焦元间必须是互斥的关系,这为信度函数组合精细化分析奠定了基础。

DSm理论加入冲突焦元的概念,使问题的描述模型也得到了扩展。在DSm理论中,融合问题的基本描述以辨识框架和约束条件决定。Θ表示融合问题的辨识框架,Θ={θ1,θ2,…,θn}是一个由n个完备假设组成的有限集,θ1,θ2,…,θn分别表示辨识框架的n个单元素。这里,以3个单元素的辨识框架为例,用维恩图表示方法对Shafer模型、自由DSm模型进行说明,如图1所示。

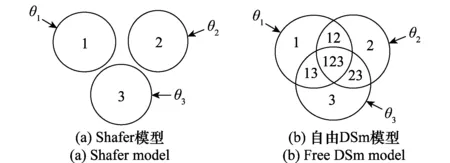
图1 模型维恩图Fig.1 Venn Diagrams of models

2.2 基于自由DSm模型的冲突表示

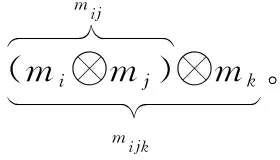
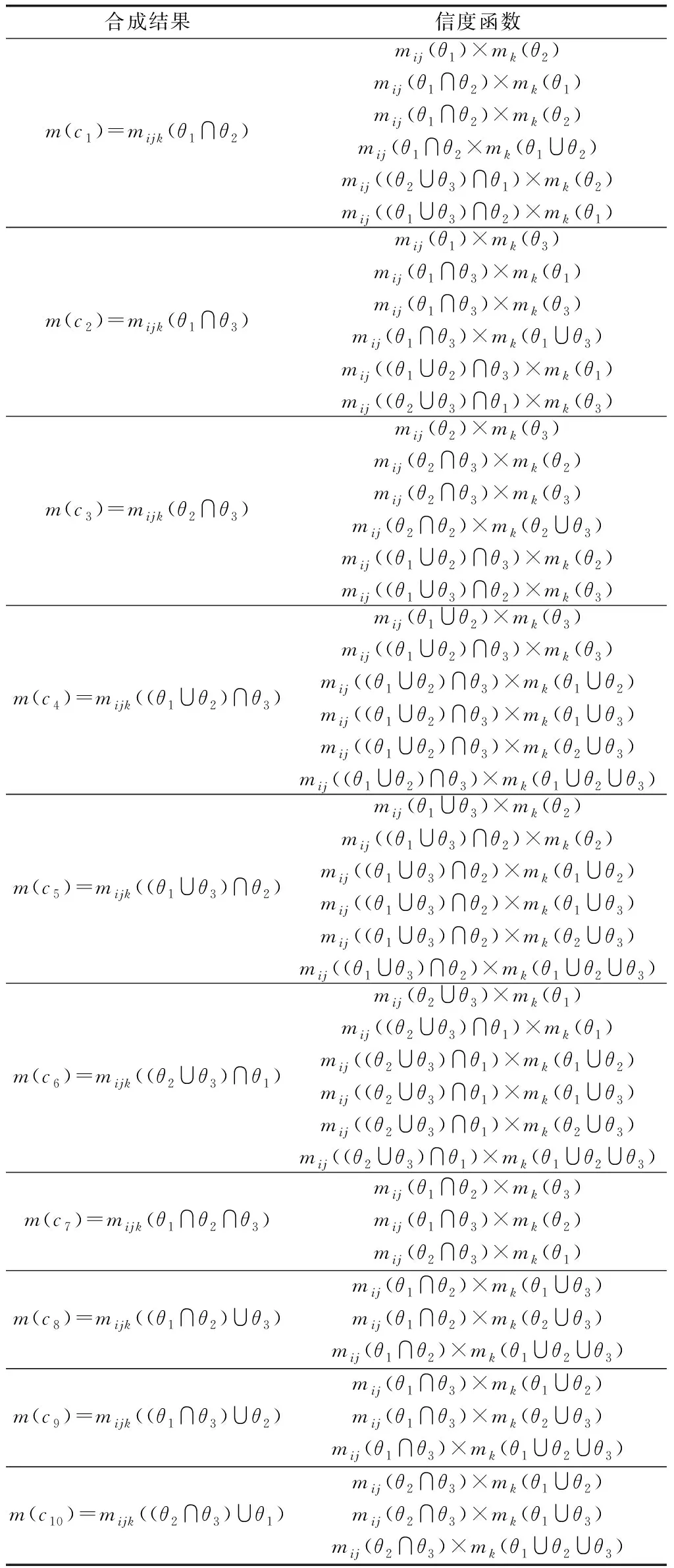
表1 冲突元素集相关的信度函数组合

3 一致性冲突证据组合规则

分布式融合结果的一致性并不是要求组合规则满足严格的结合性,而是要求组合结果具有较高的一致度。组合结果的不一致主要由于将冲突的多次不一致分配,受到Daniel的minC组合规则和Dezert的PCR规则的启发,本文提出了一种新的一致性证据融合方法。新的一致性组合规则主要思路是:假设每个融合周期内有N条证据,首先根据获取顺序对前N-1条证据基于DSmC组合规则得到证据的组合信度和先前冲突信度;然后根据一致性PCR规则加权分配先前冲突信度和当前冲突信度,得到组合结果。

假设进行分布式融合时有N个融合节点,Θ为辨识框架,不同的融合节点得到证据的顺序不同,有N条证据mi(·)(i=1,2,…,N),假设mi(∅)=0且∀A∈GΘ∅,一致性组合规则有先前信度组合及冲突保留、冲突分配两个步骤。

步骤1先前信度组合及冲突保留

(7)

由于在自由DSm模型下,超幂集DΘ中的非空集元素之间的交集不为空集,因而mDSmC(∅)恒为0。这满足了空集的基本信度分配为0的要求。此外,DΘ在交(∪)、并(∩)算子的作用下是封闭的,这也使得DSmC组合规则融合之后的信度依然满足定义中的所有DΘ元素的基本信度分配之和为1的要求。组合后得到基于证据顺序的前N-1条证据在自由DSm模型下的组合结果。组合信度包括了组合信度和冲突信度,先前组合信度相关焦元集合为{F},先前冲突信度相关焦元集合为{C}(见表1)。

步骤2信度分配

(8)

其中

(9)

4 算例分析

假设某分布式融合系统中,存在5个节点,每个节点具备信息感知和信息融合处理能力,每一个都能获得自身和其他节点感知得到的目标属性证据,但每个节点获得证据的顺序不同,如图2所示。假设辨识框架为Θ={H,N,U},模型为Shafer模型。选择了6种组合规则与本文提出方法进行对比,其中,Dempster组合规则[5]、Yager组合规则[6]、孙全组合规则[8]满足组合规则结合性,混合DSm组合规则[15]、PCR1组合规则[16]、PCR5组合规则[16]能够处理高冲突证据。

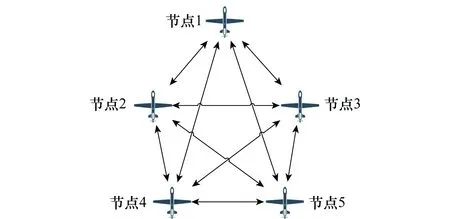
图2 分布式信息融合系统Fig.2 Distributed data fusion system

4.1 高冲突证据乱序算例

节点获得的证据如表2所示,节点1的传感器故障得到了错误的证据m1,下面通过高冲突证据算例对组合规则的一致性进行分析。

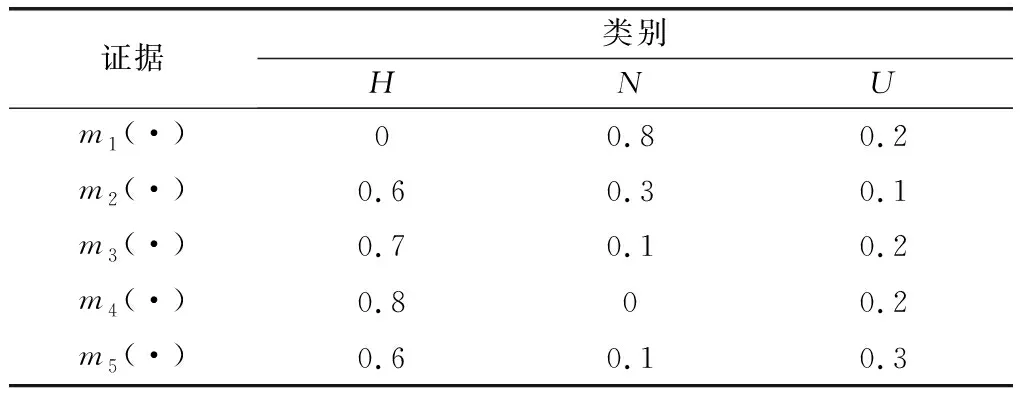
表2 不同节点获取原始证据

冲突证据是影响一致性的关键因素,本小节对高冲突证据乱序,低冲突证据顺序不变的情况进行了仿真。各节点接收证据顺序如下:

(1) 节点1m1/m2/m3/m4/m5;

(2) 节点2m2/m1/m3/m4/m5;

(3) 节点3m2/m3/m1/m4/m5;

(4) 节点4m2/m3/m4/m1/m5;

(5) 节点5m2/m3/m4/m5/m1。

各节点组合结果及一致度如表3所示。使用7种组合规则时各节点的组合结果(类别H),如图3所示。

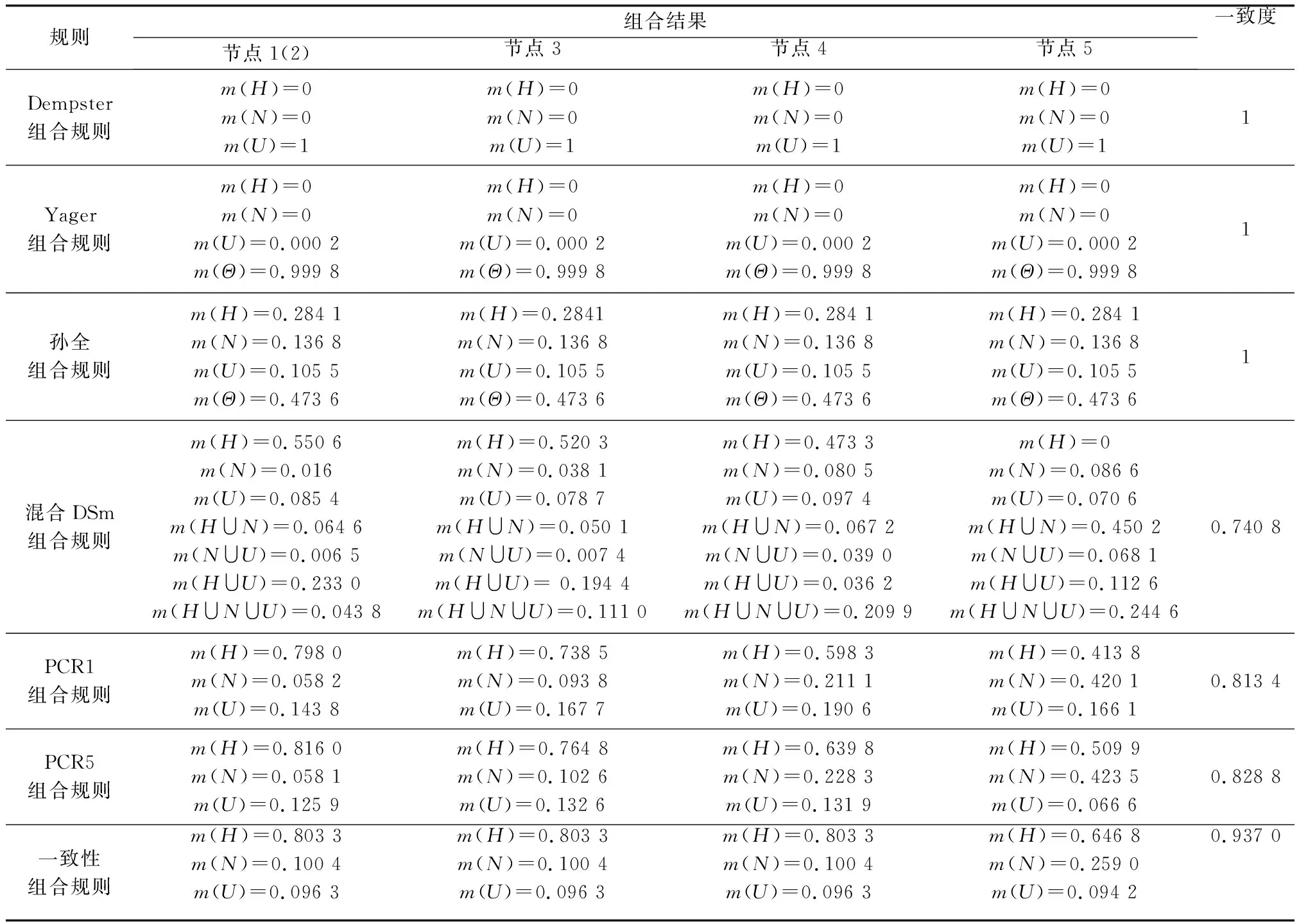
表3 各节点组合结果及一致度(Ⅰ)

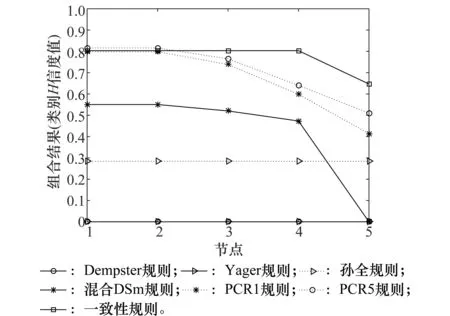
图3 高冲突算例各节点的组合结果(类别H)Fig.3 Combination results of different nodes (class H) for highly conflicting evidence

4.2 低冲突证据乱序算例

节点获得的证据如表4所示,下面通过低冲突证据算例对组合规则的一致性进行分析。各节点接收证据顺序同第4.1节高冲突乱序算例。各节点组合结果及一致度如表5所示。

使用7种组合规则时各节点的组合结果(类别H),如图4所示。

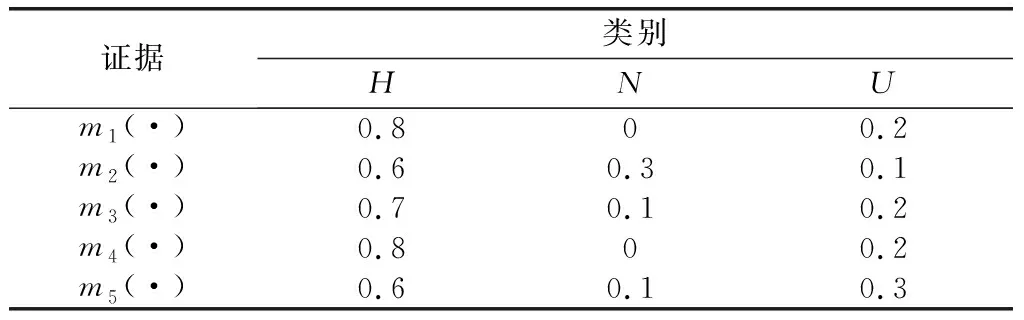
表4 不同节点获取原始证据

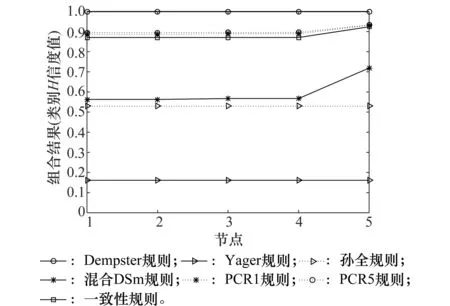
图4 低冲突算例各节点的组合结果(类别H)Fig.4 Combination results of different nodes (class H) for low conflicting evidence

4.3 结果分析

对高冲突算例,从表3和图3中可以看出,Dempster组合规则、Yager组合规则、孙全组合规则组合结果不受证据乱序的影响,一致度均为1。但Dempster组合规则对高冲突证据的处理得到了错误结论,Yager组合规则和孙全组合规则将大量信度值分配给未知Θ,没有降低结果的不确定性。因此,虽然上述3种组合规则在一致性上得到了最优,但是无法处理高冲突证据的缺陷导致其无法在实际系统中应用。混合DSm组合规则在节点1～节点4都得到了正确的组合结果,但由于混合DSm组合规则的分配策略,组合结果信度比较分散,混合DSm组合规则节点一致性只有0.725 0,节点5由于冲突证据的影响,焦元并集占据大部分信度值,模糊性增加。PCR1组合规则与PCR5组合规则在高冲突乱序算例上表现相似,一般情况下都能得到比较理想的结果,但当冲突证据为末尾证据时,两种方法都得到错误的识别结果将目标确定为U,原因是将多条证据的冲突提前分配,导致增大了末尾证据的权重。本文提出的一致性组合规则5个节点都将目标确定为H,有效地处理了高冲突证据不一致带来的问题,一致度达到0.883 8。冲突证据的位置对组合结果有一定影响,当冲突证据为末尾证据时,类别H的信度值从0.803 4下降为0.714 4,但比其他方法稳定性更高,满足不同节点组合结果的一致性。

对低冲突算例,从表5和图4可以看出,所有组合规则在低冲突证据乱序情况下都能保持较好的一致程度,这是因为证据冲突程度低,不同顺序的证据在组合过程中分配因子差异不大。Yager组合规则、孙全组合规则、混合DSm组合规则由于冲突分配给不确定性集合,决策难度较大。Dempster组合规则在低冲突情况下得到最好的融合结果。PCR1组合规则、PCR5组合规则和本文提出组合规则组合结果差异不大,得到略低于Dempster组合规则的结果。

综上,在低冲突乱序情况下,Dempster组合、PCR1组合规则、PCR5组合规则和本文提出组合规则都得到比较理想的结果。在高冲突乱序情况下,本文方法的结果比其他方法有明显提高。因此,本文方法面向不同冲突程度的乱序证据都能得到一致的组合结果。

5 结 论

针对分布式融合系统证据推理的一致性问题,本文提出一种新的冲突证据处理一致性组合规则。利用自由DSm模型对先前冲突信度进行保留,避免了多条证据的冲突提前分配带来的末尾证据权重不合理问题,对先前冲突信度和当前冲突信度进行再分配,将降低了证据顺序对不同节点一致性的影响。算例验证了本文方法的有效性。下一步,课题组将拓展一致性组合规则的应用领域,研究辨识框架、通信拓扑动态变化情况下证据理论组合规则的一致性问题。