基于模数混合的高速激光信号同步算法

朱理辰, 赵晨宁, 王继超, 安建平

(1. 北京理工大学信息与电子学院, 北京 100081；2. 中国船舶工业综合技术经济研究院, 北京 100081)

0 引 言

激光统一测控系统是将空间激光测距与激光通信深层次结合的高速传输系统[1]。作为航天测控通信领域的一项新技术,其具有带宽大、作用距离远、测量精度高、通信速率快、抗电磁干扰能力强、可快速部署等优势[2-4]。

信号同步技术是激光统一测控系统中的核心技术之一[5-6]。将成熟的数字信号处理方法运用到光信号同步中是目前一种常见手段[7]。经光接收、光电转换、信号捕获后,利用基于软件无线电思想的全数字延迟锁定环(fully digital delay-locked loop,FDDLL)技术对接收信号进行跟踪,通过估计接收信号同步码与本地同步码间的相位差和频率差,实现接收激光信号时延的精确估计[8]。但是在激光统一测控系统中,由于信号传输速率极高,单个符号持续时间在ns甚至ps量级[9]。FDDLL对于高速数据采集技术的需求会受到模数(analog to digital,AD)采样技术发展的限制。而且高速运算会占用数字信号处理器的大量运算和存储资源。特别在航空航天领域,由于空间平台上供电和数字运算资源受限,不仅需要高性能芯片支撑数据采集和运算处理,而且对运算复杂度也提出了更严格的要求。这就需要在保证性能的同时,尽可能降低数据采集速率,并设计低功耗、低片上资源消耗的信号同步算法。

目前国内外针对上述问题已进行了一些相关研究[9-16],文献[9-12]针对全数字跟踪环路提出高传输速率下的改进方案:文献[9]通过为数字锁相环定义新的规则,使其适用于高速传输系统;文献[10]将数字锁相环与TDT(timing with dirty templates,TDT)捕获算法相结合以适应于动态下的高速传输系统。以上方法都在一定意义上提升了对高速信号的同步能力,但是在数据传输速率达Gbps量级的光传输系统中仍会受到采集技术和处理复杂度的限制。文献[11]对超宽带单脉冲信号设计了一种模拟域同步方法;文献[12]针对超宽带高斯脉冲信号设计了一种模数混合捕获方法,可适用于百Mbps的高速传输系统。不过文献[11-12]并未说明更高速率的适应情况,且其主要讨论对象是超宽带脉冲同步方法。文献[13-16]对高速采集方法进行了设计,能够一定程度上减轻采样技术造成的影响,特别是文献[16]所介绍的方法可以通过并联AD实现极高速率采集。但是高速采集方法伴随着软硬件处理复杂度、系统功耗以及成本的大幅度提升。而且随着信号传输速率的进一步提升,对采集技术的要求将更加苛刻。

针对全数字处理方法在高速信号同步中的困难,本文提出了一种基于模数混合的高速信号同步技术,利用高速门电路和宽带积分电路直接在模拟域实现接收信号与本地同步码的积分清除运算,再对积分后的低频模拟信号进行采样,最后通过环路算法实现同步。仿真与分析结果表明,这种算法在保证高精度同步的同时,极大地降低了对AD采样率的需求,降低了系统功耗,并节约了数字信号处理器的运算和存储资源。同时也保留了数字信号处理器在环路参数计算方面的灵活性和高效性等优势。随着宽带运算放大器等高速模拟处理电路的发展[17-19],此算法将支持更高速率的信号同步。

目前很多热点领域如激光统一测控系统以及太赫兹宽带空间通信系统[20-22]等,其超高的传输速率需要实时有效的高速信号同步算法。本文所述同步算法可以作为这些高速传输系统接收信号同步的解决方案。

1 模数混合同步算法

本文采用强度调制直接检测方式建立激光传输链路,接收机直接检测信号的幅度,以此恢复信息,故基带电信号中不含载波项。

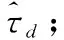
为了更清楚地分析模数混合信号同步算法,下面对接收信号模型进行说明。

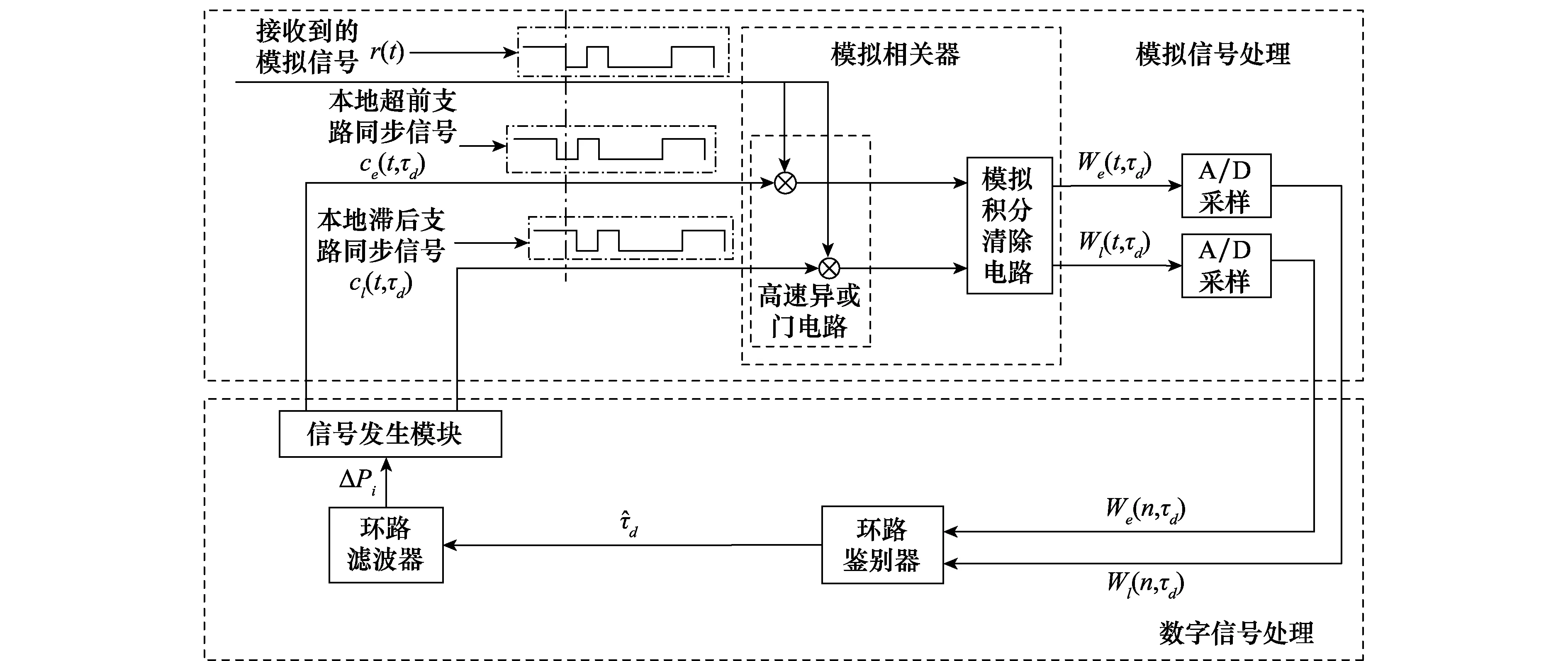
图1 模数混合同步环路原理图Fig.1 Block diagram of AD hybrid synchronization loop

接收信号r(t)表示为

r(t)=A1s(t-τ)+n(t)=

(1)

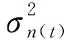
G(t)=u(t)-u(t-Tb)

(2)

式中,u(t)为阶跃函数。根据式(2),式(1)中的G(t-kTb-τ)这一项可展开为G(t-kTb-τ)=u(t-kTb-τ)-u(t-(k+1)Tb-τ)。此外,s(t)的数据格式为:每帧长度为Lbit,帧头为长度为Ntbit的同步码,其余为信息位;数据速率为Rb,则有比特周期Tb=1/Rb,数据帧周期Tframe=L×Tb,同步码持续时间Tc=Nt×Tb。

下面讨论信号发生模块产生的本地同步信号。设超前-滞后支路相关间隔为2d,本地产生的超前和滞后支路同步信号可表示为

ce(t,τd)=cp(t+d,τd)=

(3)

cl(t,τd)=cp(t-d,τd)=

(4)

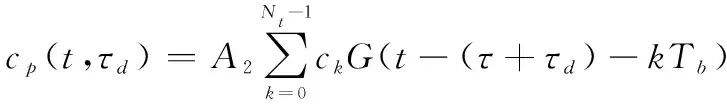
下面分别对模拟信号处理和数字信号处理两部分进行详细说明。

1.1 模拟信号处理部分

模拟信号处理的任务是完成模数混合同步算法的高速模拟相关运算,经AD采样后送至数字信号处理部分。由于相关运算后的信号速率很低,可使用低速AD采样。

首先,由于信号的取值为ck∈{0,1},所以可通过高速异或门电路完成接收信号和本地同步信号的模拟相关运算中的点乘运算。

然后通过模拟积分清除电路完成模拟相关运算中的积分运算。其中,模拟积分清除电路采用的是图2中带保持和清零功能的有源阻容(resistance-capacitance, RC)模拟积分清除电路。图2中,R和C分别是工作电阻、电容,Rf是复位电阻,S1、S2表示数控开关。积分清除电路的工作状态可由S1、S2控制:当S1打开,S2闭合时,积分清除电路处于“工作”状态,实现积分功能;当S1闭合,S2打开时,处于“清除”状态,积分结果清零;当两开关都打开时,处于“保持”状态。

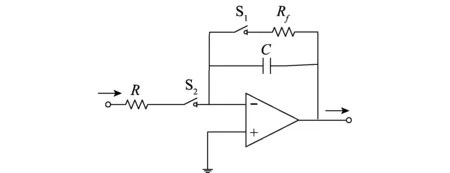
图2 带保持和清零功能的有源RC模拟积分清除电路Fig.2 Active RC analog integrator with holding and clearing function

积分、清除、保持这3种状态持续时间分别为Tcoh、Thold和Tclear(其中Tcoh与同步码持续时间Tc相等)[23],其与数据帧周期Tframe间的关系如图3所示。

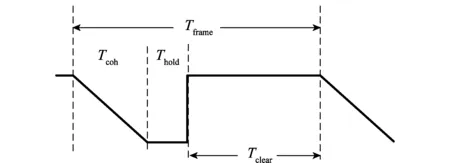
图3 每帧中积分、保持和清除3种状态持续时间示意图Fig.3 Diagram of integral, holding, and clearing durations in each frame

令Tcoh<τ0,其中τ0=R×C,以保证在该时间内积分清除电路未达到饱和状态。可推得在Tcoh内,超前支路模拟相关结果We(t,τd)为

(5)

式中,信号部分Wes(t,τd)的表达式为

(6)

其中

INTesProc=

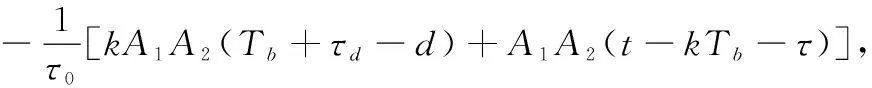
Ge(t,τd)是按式(7)定义的门函数。其表达式为

Ge(t,τd)u(t)-u(t-τd+d-Tb)

(7)

噪声部分Wen(t,τ)的表达式为

Wen(t,τd)=

(8)

(9)

式中,INTe=-A4(Tb+τd-d)+Wen(t,τd);A4=NtA1A2/τ0是一个与τd和d无关的常量。

对滞后支路结果的分析方法与超前支路类似,在单个数据帧周期内,积分清除电路输出为

(10)

式中,INTl=-A4(Tb-τd-d)+Wln(t,τd)。信号部分Wls(t,τd)的表达式为

Wls(t,τd)=

(11)

其中

INTlsProc=

噪声部分Wln(t,τd)的表达式为

Wln(t,τd)=

(12)

完成高速模拟相关运算后,对超前支路和滞后支路的积分结果We(t,τd)和Wl(t,τd)进行采样。由于已经完成了积分运算,可以使用低速AD进行采样。采样结果输入到数字信号处理器。

1.2 数字信号处理部分

数字信号处理包括环路鉴别器、环路滤波器和信号发生模块3部分。环路鉴别器根据模拟相关运算结果估计本地产生的同步信号与接收信号之间的时间偏差τd;环路滤波器据此计算调整量,并将其反馈到信号发生模块产生新的同步信号。

首先对环路鉴别器的原理进行详细说明。由式(9)和式(10)可知,当t=Tcoh时,积分过程结束,此时我们可以得到本地超前和滞后两支路同步信号与接收信号的积分结果We(Tcoh,τd)=INTe和Wl(Tcoh,τd)=INTl。当本地同步信号落后于接收信号(τd>0),有

|We(Tcoh,τd)|>|Wl(Tcoh,τd)|τd>0

(13)

当本地同步信号超前于接收信号(τd<0),又可得到与式(13)相反的结论,即|We(Tcoh,τd)|<|Wl(Tcoh,τd)|τd<0。进一步地,由式(9)和式(10)可得t=Tcoh时刻超前、滞后支路相关运算结果幅值之差

ΔW(Tcoh,τd)=

We(Tcoh,τd)-Wl(Tcoh,τd)=-2A4τd

(14)

即在每一个积分周期内,当A4确定后,时延τd决定着Tcoh时刻所对应的超前、滞后两路积分幅值之差ΔW(Tcoh,τd)的大小,且τd与ΔW(Tcoh,τd)呈线性关系。所以只要得到ΔW(Tcoh,τd),或者说得到We(Tcoh,τd)和Wl(Tcoh,τd),即可估计τd。

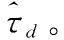
(15)

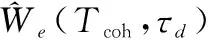
(16)

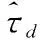
(17)

式中,BL是跟踪环路的噪声带宽。

信号发生模块使用查找表产生本地同步信号,必须保证查找表地址满足PNCO∈[0,L×2F],其中F为码相位的小数量化位数,PNCO表示信号发生模块查找表寻址相位。而且每个积分周期的首个相位地址的确定还要考虑前一个积分周期结束时最后一个寻址对应的码相位。据此可以按式(18)得到每个积分周期信号发生模块的寻址相位初值。

PNCOInit(i+1)=

(PNCOInit(i)+(LfrmPoint(i)-1)×FTW+P0(i))%(L×2F)

(18)

式中,PNCOInit(i)和PNCOInit(i+1)分别表示第i个和第(i+1)个积分周期起始时刻的信号发生模块寻址相位值;LfrmPoint(i)指的是第i次跟踪过程中一个传输帧包含的采样点数;FTW表示码相位增量控制字。式中的求余运算可以保证所有的地址都在[0,L×2F]以内。按照地址从查找表中读取预先存储的同步码,输出给模拟处理部分,经时延控制得到新的超前、滞后支路同步信号ce(t,τd)和cl(t,τd),开启下一次环路运算。以此形成模数混合的闭合跟踪环路。

1.3 模数混合信号同步算法的硬件设计

为了进一步说明算法的可行性,我们按照图1所示结构和上文所述方法对所提出的高速模数混合信号同步算法进行了硬件设计。

模拟信号处理的硬件电路设计是高速信号同步系统硬件设计的重点和难点,要求电路系统具有足够的带宽和时间控制精度。图4为模拟信号处理部分硬件系统设计框图。图4中,经光电转换后得到的接收信号通过A口输入高速逻辑门芯片HMC844(支持45 Gbps数据);本地同步信号由数字信号处理器中的信号发生模块产生,经时延控制芯片HMC856LC5(支持28 Gbps数据)得到超前支路和滞后支路信号,通过B口输入高速逻辑门。高速逻辑门完成对两路输入信号的异或运算,然后将运算结果输入至高速模拟积分清除电路。

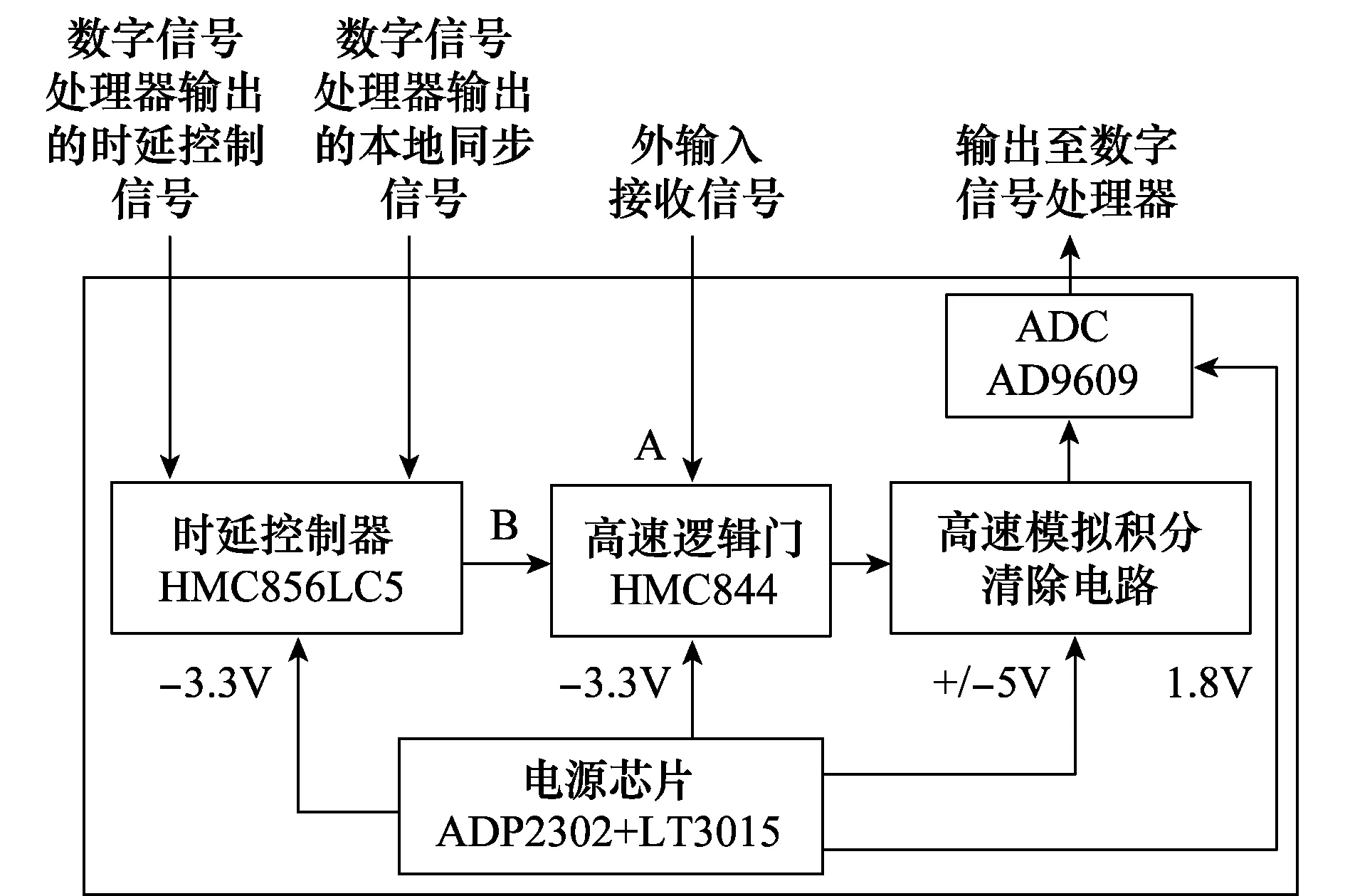
图4 模拟信号处理部分硬件系统设计框图Fig.4 Block diagram of the analog signal processing hardware system

按照图2所示结构设计高速模拟积分电路。本文选用ADI公司的AD8003宽带运算放大器和电容、电阻、开关共同构成带有保持、清除功能的模拟积分清除电路。利用数控开关和结型场效应管J2N4393控制积分清除电路的工作状态,以实现定时对积分结果进行保持和清除的功能。高速模拟积分电路设计原理图如图5所示,可按照所设置的Tcoh、Thold和Tclear这3个参数完成如图3所示的周期性定时积分、保持和清除功能,输出超前、滞后相关结果We(t,τd)和Wl(t,τd)。

使用低速AD芯片AD9609对We(t,τd)和Wl(t,τd)采样,然后送至数字信号处理器,完成后续处理。由于数字部分的处理速率较低,且可利用较为成熟的可编程芯片来完成,所以设计难度相对较低,出于文章简洁性的考虑,不对这一部分进行详细讨论。

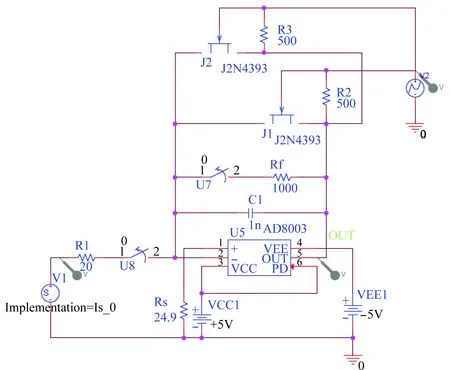
图5 带有保持清除功能的高速模拟积分电路原理图Fig.5 Schematic diagram of high speed analog integrator with holding and clearing functions

2 对比分析

本文采用通断键控调制,数据速率Rb=2.5 Gbps,数据帧长L=8 192 bit,采用长度Nt=256 bit的伪随机序列作为同步码,同步码位于每帧帧头,其余为控制信息和数据位。下面分别在信号同步精度、系统功耗以及数字处理器运算复杂度3个方面对模数混合信号同步算法与全数字同步算法(即前文提到的FDDLL算法)进行对比分析。

2.1 同步精度对比分析

本文提出的模数混合信号同步算法仅对高速信号相关运算采用模拟处理,对环路鉴别、环路滤波等仍采用数字处理。所以只要分析在环路鉴别前的处理对同步精度的影响即可。

典型的FDDLL算法同步精度[24]为

σFD=

(19)

式中,BL和d是环路滤波器参数;Tcoh表示积分时间,两种算法的这3项参数是一致的,目前需要讨论的是载噪比C/N0。假设模数混合处理方式与全数字方式的带宽一致,则可将C/N0对比转化为信噪比(signal-to-noise ratio, SNR)对比。两种算法区别主要在于积分/累加运算后的信噪比这一项。

对于全数字算法,采样频率以fs表示,在同步码持续时间Tc内可以采集Ns个样点。完成相关运算后,全数字算法信噪比为SNRFD,模数混合算法信噪比为SNRmix,二者关系为

(20)

由于积分结果本身近似线性,对积分结果做线性估值,其误差可认为是0,即线性估值不引入新的误差。

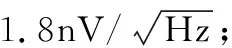
综上,相比于全数字算法,模数混合同步算法不会造成同步精度下降。

2.2 功耗对比分析

由于现场可编程门阵列(field programmable gate array, FPGA)具备强大的并行处理能力,适用于高速处理系统,故本文使用FPGA作为数字信号处理器。传统的FDDLL算法

需要使用高速AD对接收信号采样,采样率至少为5 Gsps。为满足时序要求,FPGA需对采样信号做至少1∶32串并转换,转换为低速并行信号后方可处理;而模数混合同步环路要求AD采样率大于25 000/8 192×2=0.610 35 Msps即可。

对全数字同步算法和模数混合信号同步算法的实现方案进行整系统功耗对比。分别以采样速率5 Gsps的EV10AQ190芯片和采样速率20 Msps的AD9609芯片进行数据采集(AD量化位数均为10位)。经调研分析,得到如表1、表2所示结果。对比结果显示,在文中所设置的参数下,模数混合信号同步算法的系统功耗约为全数字同步算法的30%,更适于空间传输平台等功耗受限环境。

表1 全数字算法功耗

表2 模数混合算法功耗

2.3 数字处理器运算复杂度对比分析

对于空间系统而言,不仅功耗受限,可用的数字处理资源也低于地面系统。尤其在卫星通信、深空通信领域,可用的FPGA等数字信号处理器件性能有限,而多片FPGA互联不仅增加了功耗,也会使系统更加复杂,不适于空间平台使用。故降低数字信号处理复杂度也很有必要。

考虑FDDLL中的数控振荡器和伪码发生器的功能相当于本文设计的模数混合同步环路中的信号发生模块。假设两种算法在M次循环后都可完成环路入锁。表3和表4分别给出了两种算法的运算复杂度对比结果和FPGA资源开销对比结果(除同步算法外,还包括外设配置、时钟和复位控制等功能的资源开销)。由表3可知,

模数混合算法的复杂度从FDDLL的O(NtM)减少至O(M)。Nt越大,则模数混合同步算法在运算复杂度方面的优势越明显。由表4可知,模数混合算法节约了85%以上的逻辑资源、67%的存储资源以及约40%的总线资源。在高速同步处理中,模数混合算法对FPGA性能的要求远低于全数字算法。

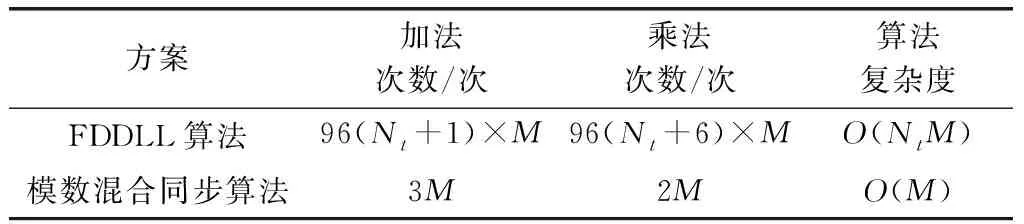
表3 两种算法的环路运算复杂度比较

表4 两种算法的资源开销对比

3 仿真分析

鉴于PSpice软件对于高频电路仿真的优越性和Matlab对于数字仿真的便利性,本文使用PSpice和Matlab联合仿真。首先对模拟电路处理过程进行仿真分析;然后对模数混合同步环路整体进行仿真,观测不同噪声下的同步精度,并与全数字算法进行对比。仿真参数与第2节所使用参数一致。

图6是高速激光信号产生和采集系统,用于产生模数混合信号同步算法仿真所需数据。系统使用高速信号生成板卡(见图6中的 编号①)产生2.5 Gbps的二进制启闭键控(on-off keying, OOK)调制信号,经电/光转换为1 550 nm波长的激光信号(见图6中的编号②),再通过光天线(见图6中的编号③)进行发送和接收,然后经光/电转换为基带电信号(见图6中的编号②),使用采样速率达80 Gsps的高速示波器采集信号(见图6中的编号④)。

图6 收发设备与光天线Fig.6 TR device and optical antenna

3.1 模拟电路处理过程仿真分析

采集到的样本数据波形如图7所示。使用采集到的样本数据作为输入信号,经异或运算后按照图5所示的电路结构对模拟相关运算功能进行仿真,结果如图8所示。

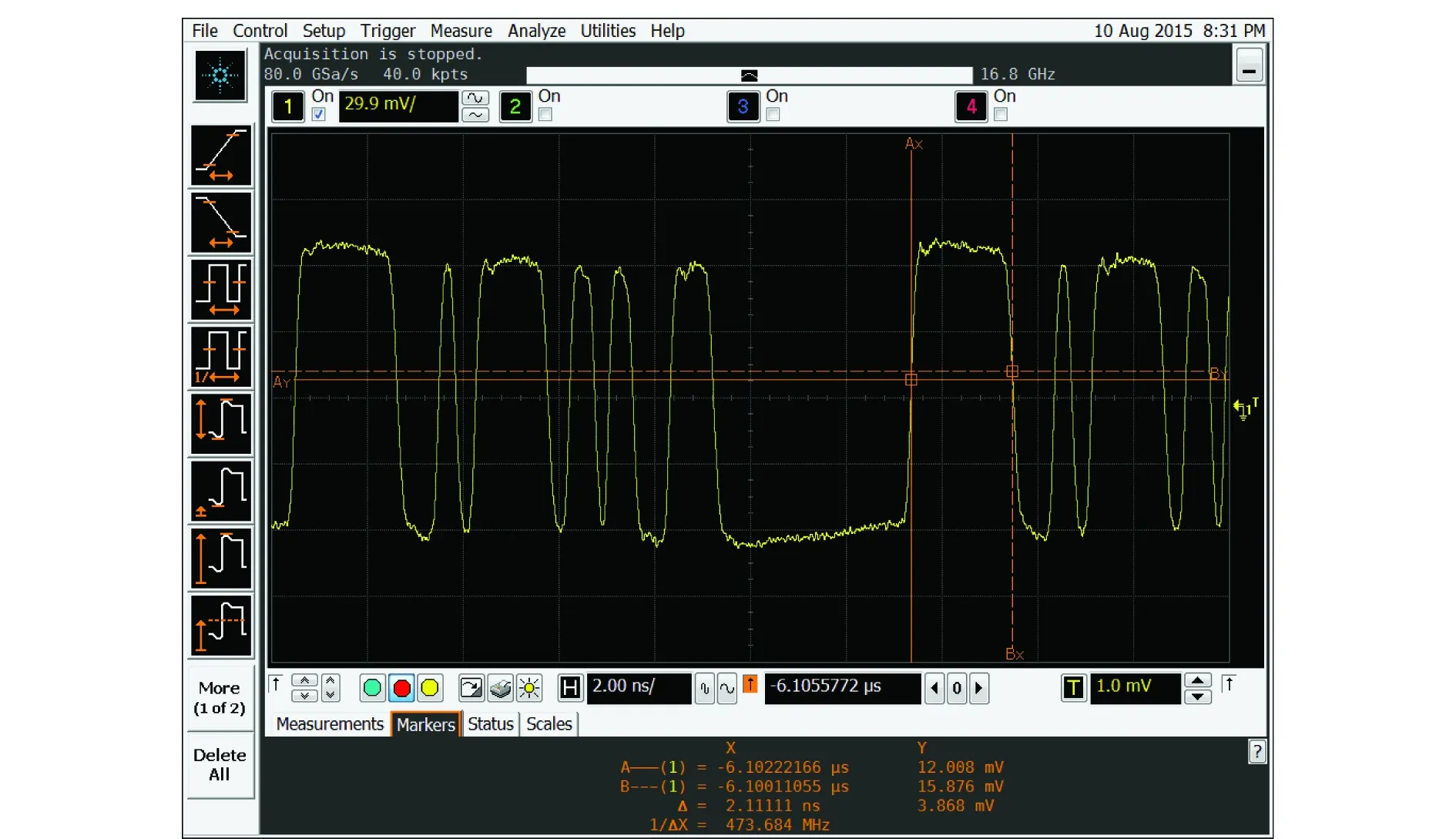
图7 光电转换后信号波形Fig.7 Waveform after photovoltaic conversion

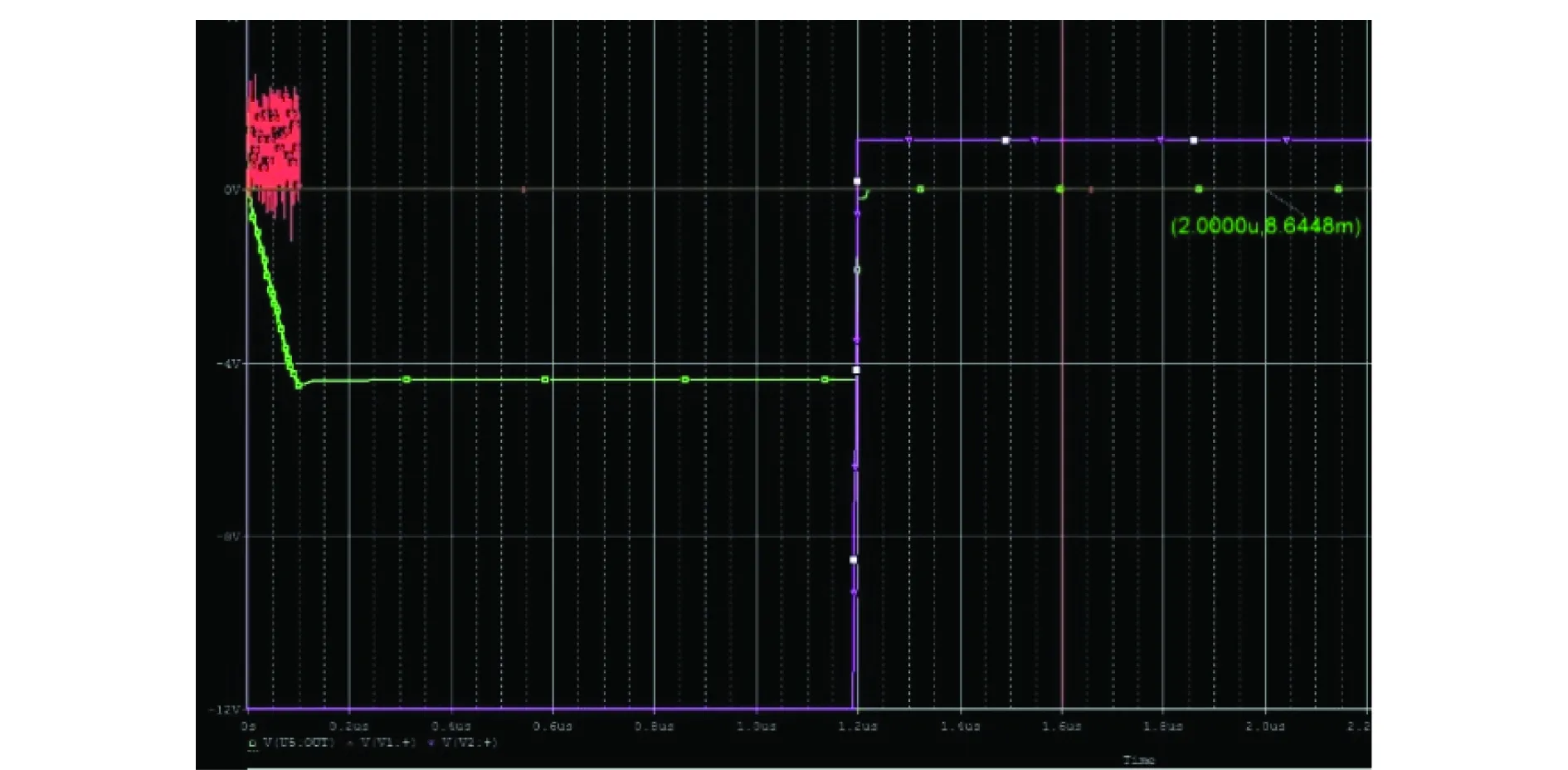
图8 积分结果的保持和清除功能Fig.8 Holding and clearing function of integral

图8中红色线表示积分清除电路输入信号,即本地同步码与接收信号异或运算结果;绿色线表示积分清除电路输出结果;粉色线表示复位信号。有效积分时间均在积分清除电路的线性工作区;在积分过程结束后积分清除电路进入保持状态;加入复位信号后,积分清除电路输出结果随之清零。虽然由于场效应管导通电阻分压,清零结果不能完全达到理想的0值,但是基本可以保持在10-2V以内,属于允许的误差范围。

3.2 模数混合同步环路仿真分析

为了分析模数混合同步环路的同步精度,在不同的Eb/N0条件下进行闭环仿真。仿真条件设为Eb/N0=-15 dB,-10 dB,-5 dB,0 dB,5 dB,10 dB。图9为在上述条件下的环路跟踪曲线,即环路鉴别器的输出结果。从图9可以看出,各条跟踪曲线均在0值附近抖动,说明环路已经入锁,且抖动随着Eb/N0的提高而降低。

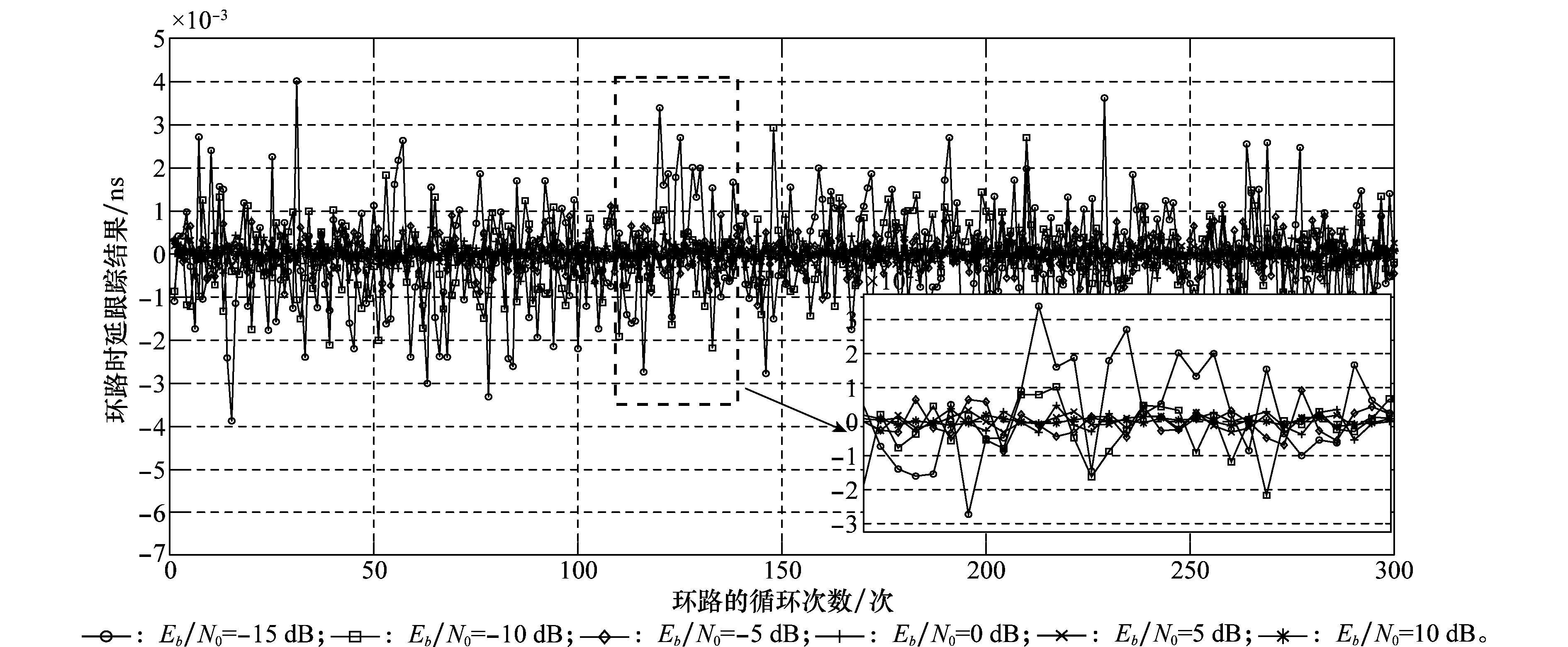
图9 同步环路的环路时延跟踪曲线Fig.9 Time-delay curve of the synchronization loop

在相同的仿真环境下,使用FDDLL算法对相同数据帧结构的信号进行同步,按文献[24-25]所述方法计算得到其同步精度理论值,并与模数混合算法同步精度进行对比,图10为两种算法同步精度对比结果。由图10结果可知,当Eb/N0≥-10 dB时,模数混合算法同步精度达80 ps以内。随着Eb/N0的增加,精度进一步提升,甚至可达ps量级,与全数字算法相比在性能上几乎没有损失,与理论分析结果一致。

由于模数混合算法与全数字算法在鉴相与环路滤波处理上完全一致,所以即便采用其他类型的环路鉴别和环路滤波算法(见文献[9]所述算法),二者的性能也是一致的。

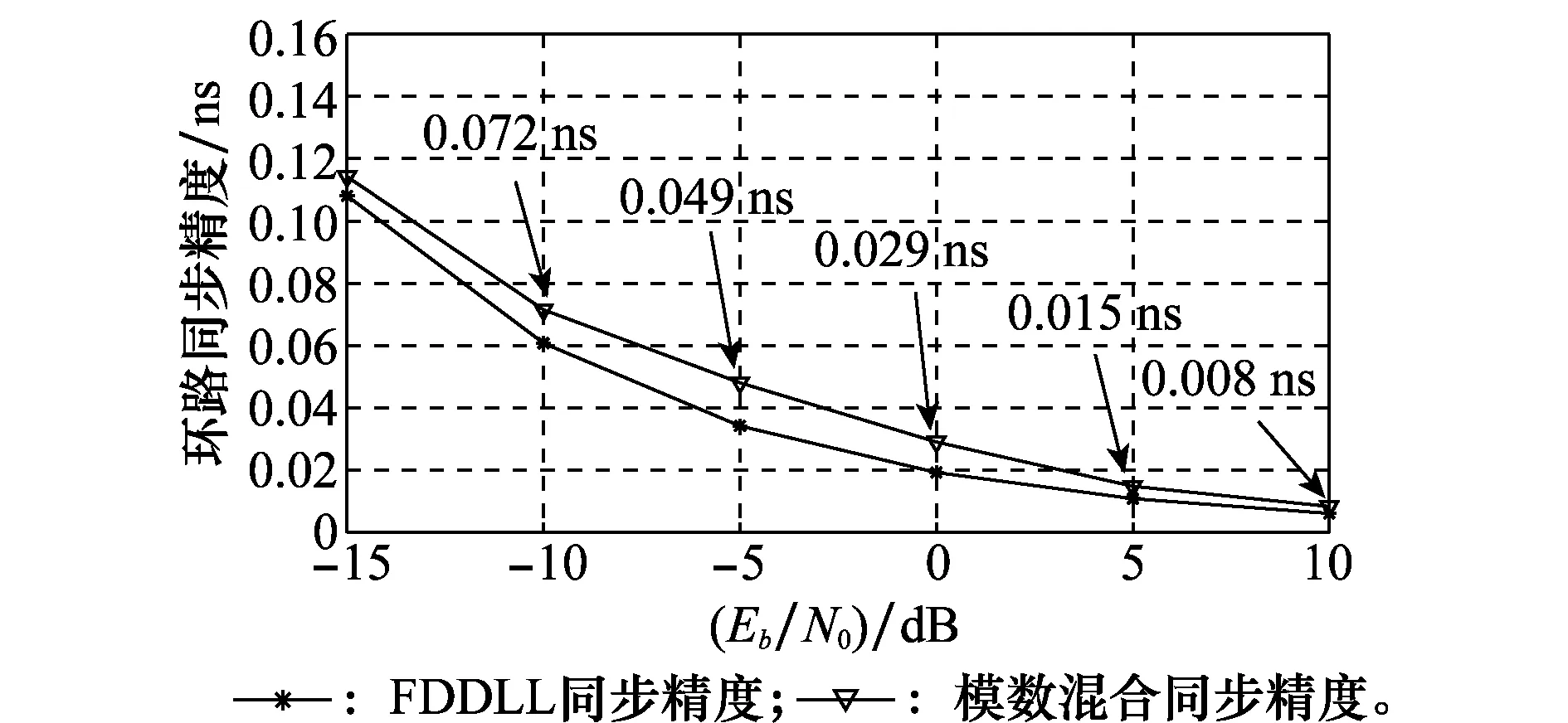
图10 同步精度对比图Fig.10 Comparison chart of synchronization accuracy

4 结束语

本文提出的基于模数混合的高速信号同步算法利用模拟域的异或和积分运算以及基于线性估值原理的积分峰值插值算法,在保证性能的同时有效地简化了数字信号处理模块的结构,成倍降低了同步环路的运算复杂度,节约了数据采集与处理资源,并降低了系统功耗。这种模数混合的同步算法可有效解决高速传输系统对于高采样率的需求与高速AD采样技术发展瓶颈的矛盾,在激光统一测控、太赫兹宽带空间通信等需要完成高速数据传输的领域中具有广泛的应用前景。