求解约束优化问题的协同进化教与学优化算法
2018-10-15刘三阳靳安钊
刘三阳 靳安钊
约束优化问题是科学研究和工程应用领域经常遇到的一类数学规划问题,它广泛存在但又难以求解,因此对求解约束优化问题有效方法的研究具有重要的理论和实际意义.目前存在的约束优化算法大致可以分为两类:传统优化算法和现代智能优化算法.传统优化算法大多是基于梯度信息的寻优方法,如可行方向法、投影梯度法和既约梯度法等[1].它们对于不可导,可行域不连通,甚至没有显式表达式的问题束手无策.现代智能优化算法主要包括差分进化算法(Differential evolutionary,DE)[2]、粒子群算法(Particle swarm optimization,PSO)[3−5]、遗传算法 (Genetic algorithm,GA)[6]、蚁群算法(Ant colony optimization,ACO)[7]、人工蜂群算法(Artificial bee colony,ABC)[8]等.近年来,现代智能算法得到了广泛的研究,在求解约束优化问题方面取得了显著的成效.
大多数现代智能优化算法都是一种无约束搜索技术,将其与约束处理技术结合的过程中需要引入一些额外的参数,这些参数通常由使用者决定,选取合适的参数一般需要经过多次试验不断调节.
罚函数法是应用最广泛的约束处理技巧,其主要思想就是通过对目标函数f(x)增加惩罚项p(x)来构造适应度值函数fitness(x).惩罚适应度值函数的构造过程会引入参数罚因子w,罚因子选取太小则个体的适应度值主要由目标函数决定,此时群体可能滞留在不可行区域,很难找到最优解;罚因子选取太大则种群快速进入可行域,从而忽略了对不可行区域的搜索,这样就不能充分利用不可行解提供的信息[9],从而很难找到最优解.
此外,还有很多约束优化问题带有等式约束,等式约束的出现使得约束优化问题的求解变得更加困难.等式约束的出现极大地缩小了可行区域的范围,对搜索最优解带来了极大的困难[10].一般的等式约束处理技术都是将等式约束转化为不等式约束,即将等式约束h(x)=0转化为

其中,δ为等式约束的约束容忍度参数,一般取较小的正数.这一转化过程改变了可行域的拓扑结构,δ的大小直接决定了这种拓扑结构改变程度,也决定了可行区域的大小.因此设置合适的约束容忍度参数δ是十分必要的,然而参数δ的合理设置是一项十分困难的工作.
基于以上的这些不足,本文提出了一种求解约束优化问题的协同进化教与学优化算法(Co-evolutionary teaching-learning-based optimization algorithm,CTLBO).该方法在基本教与学优化算法过程中加入了一个随机变异搜索的自我学习机制,增强了算法局部搜索能力.文章首次提出将约束容忍度参数加入进化参数集中和罚因子一起自动进化,避免了人工调节约束容忍度参数的困难,同时也实现了约束容忍度参数自适应地进化,有效地提高了求解约束优化问题的效率,尤其是含有等式约束的优化问题.同时在计算个体适应度时,将已有协同进化算法适应度值公式中的可行个体均值项替换为可行个体的方差,并根据进化时期的不同阶段,采用不同的适应度值计算公式,有效地保证了种群的多样性.
1 基本教与学优化算法
教与学优化算法(Teaching-learning-based optimization,TLBO)[11−12]由 Rao等于 2010年提出,它模拟了教师给学员教学的过程.教与学优化算法具有参数少、算法简单、易理解和求解精度高等特点.自教与学优化算法提出以后,研究人员对其进行了深入研究,并提出了许多改进算法[13−15],这些算法都取得了较好的效果.
教与学优化算法中的教师和学员相当于进化算法中的个体.教师是适应度值最好的个体,学员学习的每一个科目对应于一个决策变量.
1.1 教学阶段
学员通过两个方面提高自己的成绩,向教师学习和向同学学习.教学阶段是向教师学习的过程,学习阶段是向其他学员学习的过程.假设在第k次迭代的过程中,Mk是学员的平均成绩,Tk是教师.此时学员将会根据全体学员平均成绩与教师之间的差距来进行学习,差距由下式给出:
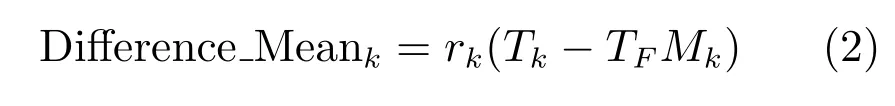
其中,rk是0到1之间的随机数,TF是一个学习因子,取值为1到2之间的随机数.实验表明,当TF按照下式进行1或2的随机取值时算法取得的结果更好:
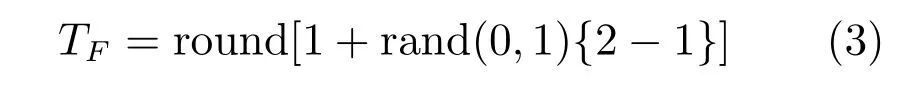
在教学阶段,学员按照下面式子更新自己的成绩:

如果更新后Xnew对应的函数值优于Xold对应的函数值,则接受Xnew,否则拒绝Xnew.
1.2 学习阶段
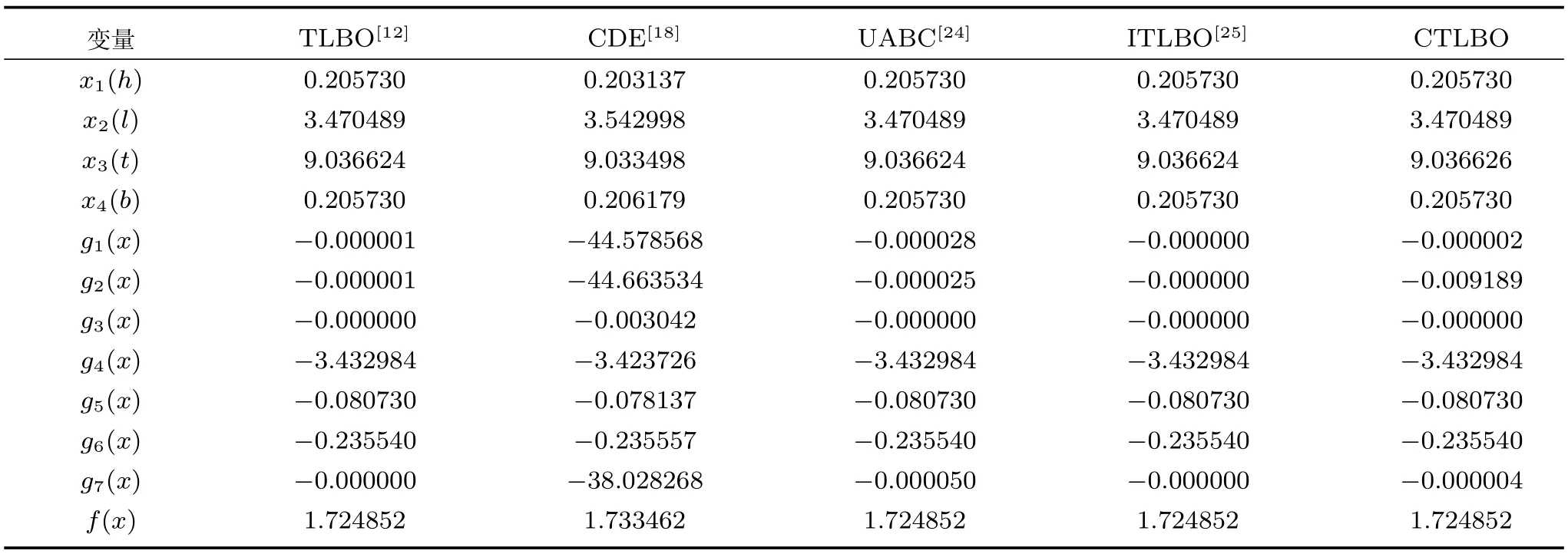
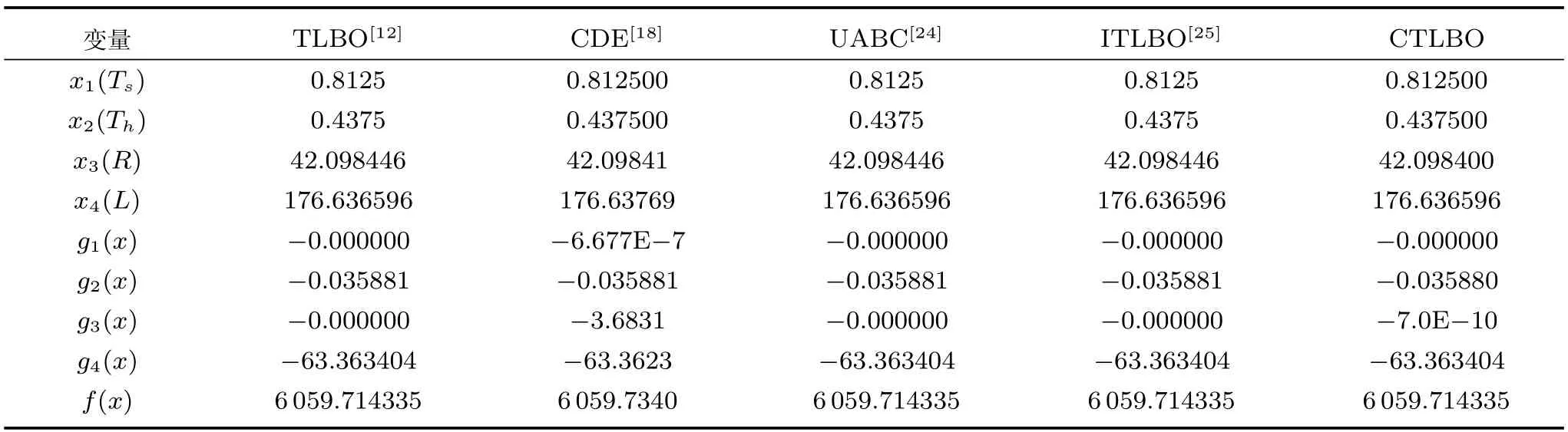
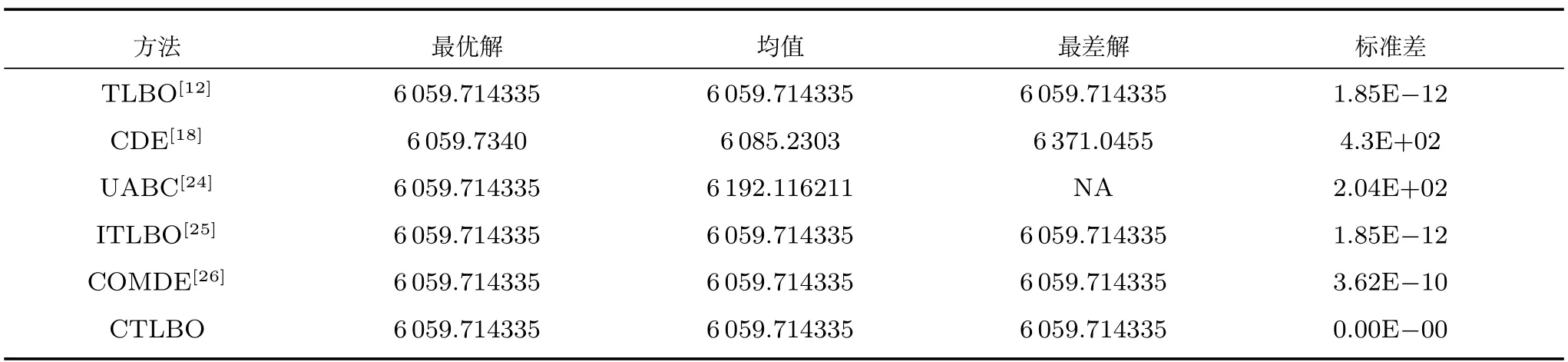
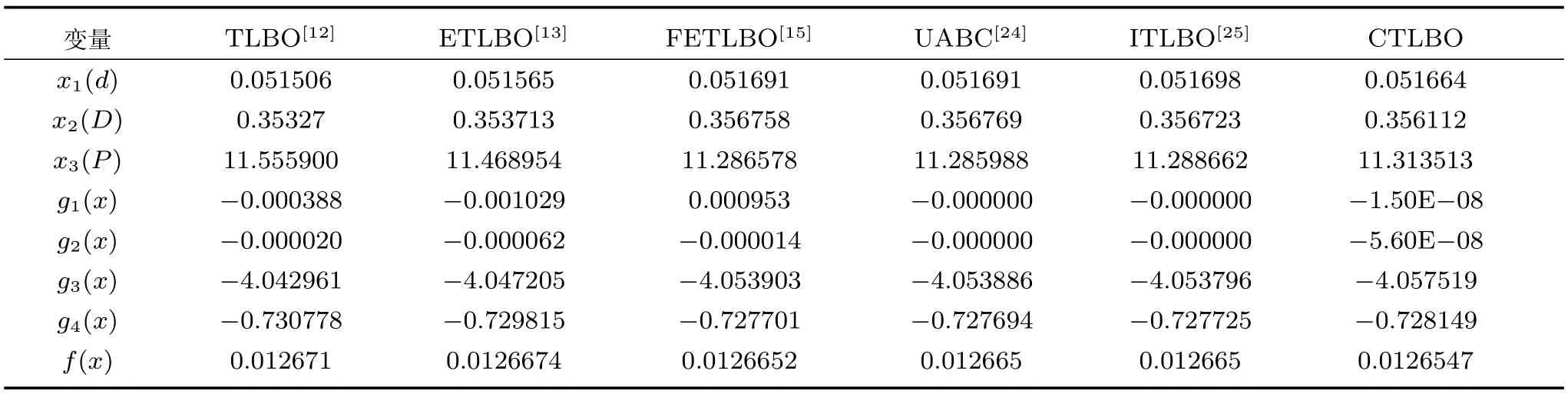
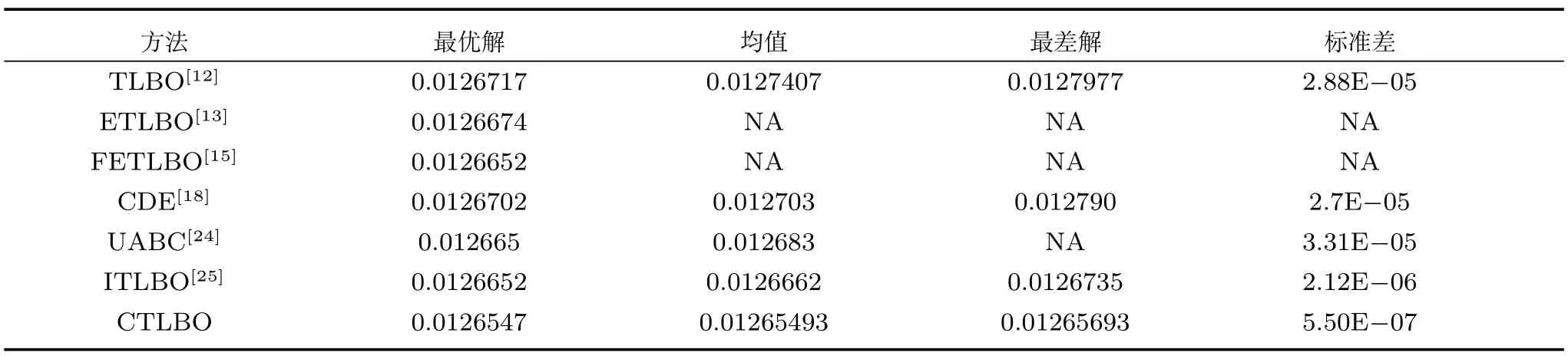
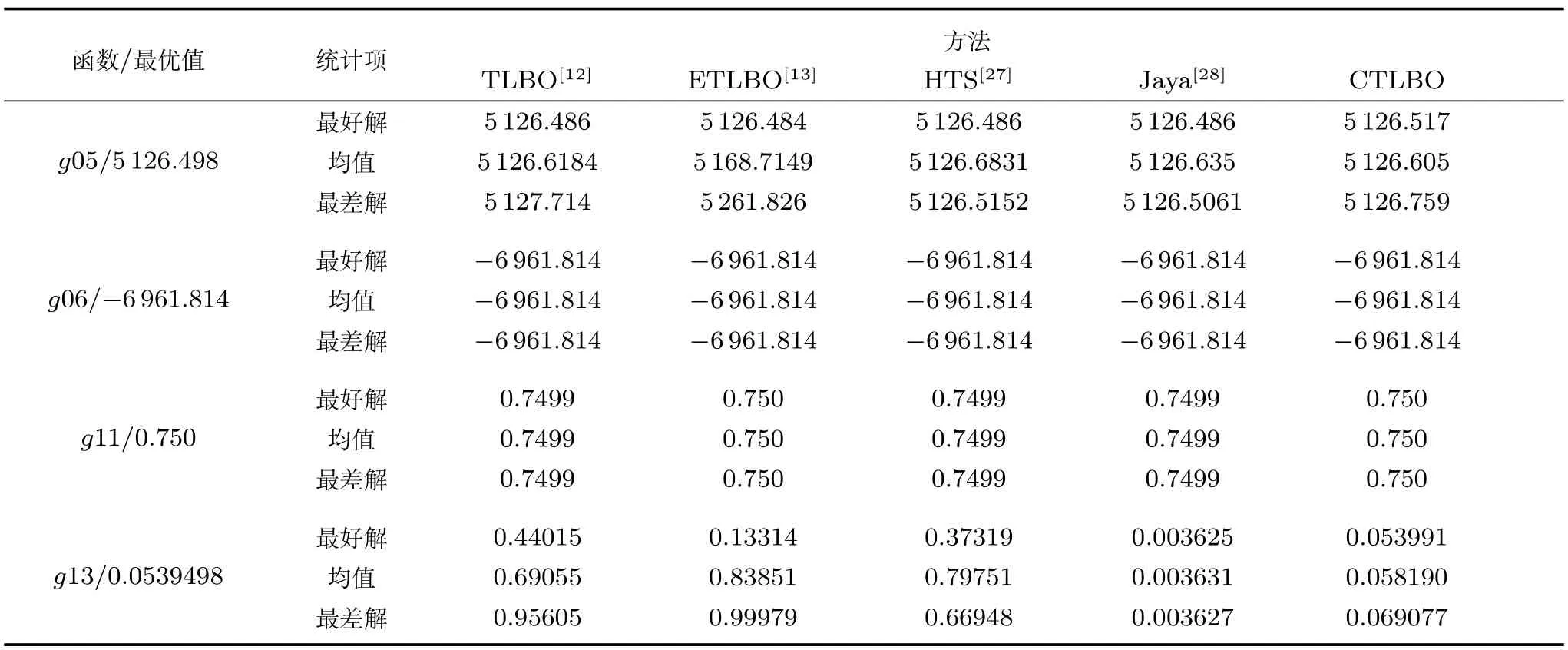
在学习阶段,学员按照下面方式进行更新成绩:对于学员Xi,随机选取一个学员,如果f(Xi) 否则 如果更新后Xnew,i对应的函数值优于Xold,i对应的函数值,则接受Xnew,i;否则,拒绝Xnew,i,其中,i=1,2,···,NP. Coello[16]提出了一种求解约束优化问题的协同进化遗传算法,He等[17]提出了求解约束优化问题的协同进化粒子群算法,Huang等[18]提出了求解约束优化问题的协同进化差分进化算法(Coevolutionary differential evolution,CDE).这些算法在求解工程约束优化问题时取得了较好的结果.本文基于这些算法提出一种协同进化教与学约束优化算法,图1展示了算法模型. 图1 算法模型Fig.1 Algorithm model 在协同进化教与学约束优化算法中,班级C2包含M2个学员,班级C1包含M2个子班级,每个子班级包含M1个学员.班级C2中的学员Bi的成绩代表着班级C1中子班级C1,i的学员进化过程中的罚因子ω和约束容忍度δ.在协同进化的每一代,班级C1中的学员首先进行自我学习过程,然后使用班级C2提供的参数集用教与学优化算法进化G1代.当班级C1完成G1代进化之后,班级C2中每个学员的适应度值根据其所对应的C1中的子班级学员位置分布情况进行更新,然后对班级C2用教与学优化算法进化一代.重复上述进化过程,直到达到最大进化代数G2. 用教与学优化算法进化班级C1时,在基本教与学优化算法中加入了一个增加算法搜索能力的随机变异自我学习机制.对班级C1,j的每一个学员Xi=(xi,1,xi,2,···,xi,n),随机选取其第j维变量xi,j构造Xnew1如下: 如果 fitness(Xnew1) 如果 fitness(Xnew2) 对于下面的约束优化问题: 根据Richardson等[19]提出的罚函数构造准则,考虑每个解的约束违反量和约束违反数目,构造下面适应度值函数: 其中,sum_viol(x)代表解x所对应的约束违反量,num_viol(x)代表解x所对应的约束违反数目,ω1,ω2分别是它们对应的罚因子. 对于约束违反量,按下面方式得到: 其中,N=n+p,此处假设所有的等式约束已经按式(1)转化为了不等式约束. 对班级C1的每个学员按式(8)确定的适应度函数值使用TLBO算法进化一代. 班级C2中的每一个学员代表一个参数集(ω1,ω2和δ).当班级C1中的子班级C1,j进化G1代之后,班级C2中学员Bj的适应度值按下面方式确定: 1)当子班级C1,j中至少含有一个可行解时,Bj称为有效学员,适应度值可以分两个阶段计算:进化初期阶段和进化后期阶段.进化初期阶段,算法目标是增加可行解数量的同时增加种群多样性,此时Bj的适应度值函数可以表示为 进化后期阶段,算法目标是尽快收敛到最优解,此时Bj的适应度值函数可以表示为 其中,objectivej,i表示子班级C1,j中可行解i的目标函数值,mean_objectivej表示子班级C1,j中可行解目标函数值的均值,num-feasible表示子班级C1,j中可行解的数目.由概率统计知识可知,方差比均值更能反映种群的波动情况.与已有协同进化算法[16−18]中的适应度值函数 2)当子班级C1,j中不存在可行解时,则称Bj为无效学员,此时Bj适应度值函数如下 其中,max(Pvalid)表示有效学员的最大目标函数值,表示C1,j中学员成绩的约束违反量之和,表示C1,j中学员成绩的约束违反数目之和.此时种群不存在可行解,算法的首要目标是使种群搜索到可行解,因此具有较小约束违反度的个体优先被选择.max(Pvalid)项的存在保证了最优可行个体始终优于不可行个体,从而使种群在选择过程中优先选择可∑行个体,进而使算法在搜索过程中偏向可行区域.num_viol项的存在可以使约束违反度较小的个体优先被选择.因此式(12)可以保证种群朝向可行区域搜索,从而加快算法的寻优速度. 通过以上对协同进化教与学约束优化算法的描述,算法流程如图2所示. 为了验证算法求解含有等式和不含等式约束优化问题的性能,本文对13个标准测试函数(测试函数见文献[20])中带有等式约束问题g05,g11,g13和不带等式约束问题g06以及三个工程问题进行了求解.此处仅给出三个工程优化问题的数学表示. 问题1.(Welded beam design problem) 问题1取自Coello[16]的焊接梁设计最小费用问题,模型如图3所示. 它含有4个决策变量h,l,t和b,x1代表h,x2代表l,x3代表t,x4代表b,问题可以用下面优化问题表示: 图2 算法流程Fig.2 Flow chart of CTLBO 图3 焊接梁模型图Fig.3 Model of welded beam 问题2.(Pressure vessel problem) 问题2取自于工程上的压力容器设计最小费用问题,它的数学表示由Kannan[21]给出,模型如图4所示. 图4 压力容器模型Fig.4 Model of pressure vessel 其中,x1表示Ts,x2表示Th,x3表示R,x4表示L,x1和x2的值取为整数然后乘以0.0625,问题可以用下面优化问题表示: 其中,1≤x1≤99,1≤x2≤99,10≤x3≤200,10≤x4≤200. 问题3.(A tension string design problem) 问题3是工程上的最小化张力弦的重量问题,模型如图5所示. 图5 最小化张力弦模型Fig.5 Model of tension string 它由Arora[22]和Belegundu等[23]给出了数学表示,其中x1代表d,x2代表D,x3代表P,问题可以用下面的优化问题表示: 其中,0.05≤x1≤2,0.25≤x2≤1.3,2≤x3≤15.本文算法参数设置如下:M1=50,M2=10,G1=30,G2=8,对于问题1和问题2中取ω1,min=ω2,min=0,δmin=10−6,ω1,max=ω2,max=1000,δmax=10−2.问题3中取ω1,min=ω2,min=5000,δmin=10−6,ω1,max=ω2,max=25000,δmax=10−2.问题g05 中取ω1,min=ω2,min=1000,δmin=10−6,ω1,max=ω2,max=3000,δmax=10−2.问题g06中取ω1,min=ω2,min=0,δmin=10−6,ω1,max=ω2,max=10000,δmax=10−2.问题g11中取ω1,min=ω2,min=0,δmin= 10−10,ω1,max=ω2,max=10,δmax=10−5.问题g13中取ω1,min=ω2,min=0,δmin=10−8,ω1,max=1,ω2,max=0.1,δmax=10−3. 对于问题1~3,算法独立运行30次,它们的最优解未知,只有目前求得的最优解作为参考.运行结果如表1~6所示(NA表示原文没有提供具体数据). 对问题g05,g06,g11和g13独立运行30次,运行结果和其他算法比较如表7所示. 通过对表1~6的实验结果进行对比,协同进化教与学约束优化算法对三个工程问题求得了更好的解,并且在求解精度和稳定性上都要优于表中列出的算法,其标准差明显小于文章列出的比较算法.通过表7可以看出,算法在对4个标准测试函数g05,g06,g11和g13的求解过程中也表现出了良好的性能.对函数g06和g11,本文算法和对比算法达到了同样好的效果,对其他两个函数,本文算法的求解结果要优于其他对比算法. 本文在基本教与学优化算法中加入了一种自我学习机制,然后对已有协同进化算法的适应度值函数进行改进,提出了一种可以增加种群多样性的适应度值函数,并首次提出将等式约束对应的约束容忍度参数加入到协同进化参数集来实现参数自适应进化,避免了人工调整参数的困难.在此基础上提出了一种求解约束优化问题的协同进化教与学约束优化算法(CTLBO),该算法结合了协同进化算法和教与学优化算法的优良特性,在算法过程中没有引入额外的参数,保持了教与学优化算法参数较少这一特点.对三个等式约束优化问题和4个不等式约束优化问题进行了仿真分析,并与其他一些算法进行比较,结果表明本文所提出的算法在求解带有等式约束和不等式约束的优化问题时具有较好的性能,其求解精确度和稳定性较文中列出的算法也有所提高. 表1 不同方法求得问题1最优解的比较Table 1 Comparison of the best solution for Example 1 found by different methods 表2 不同方法求得问题1结果统计表Table 2 Statistical results of different methods for Example 1 表3 不同方法求得问题2最优解的比较Table 3 Comparison of the best solution for Example 2 found by different methods 表4 不同方法求得问题2结果统计表Table 4 Statistical results of different methods for Example 2 表5 不同方法求得问题3最优解的比较Table 5 Comparison of the best solution for Example 3 found by different methods 表6 不同方法求得问题3结果统计表Table 6 Statistical results of different methods for Example 3 表7 不同方法求得问题g05,g06,g11和g13最优解的比较Table 7 Comparison of the best solution for exampleg05,g06,g11 andg13 found by different methods

2 协同进化教与学约束优化算法(CTLBO)
2.1 算法模型
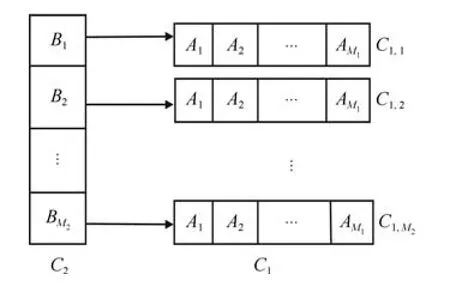
2.2 自我学习过程
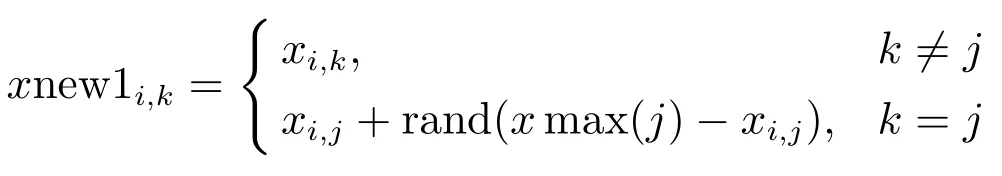
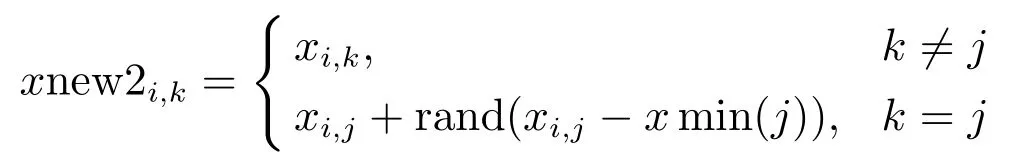
2.3 进化班级C1



2.4 进化班级C2

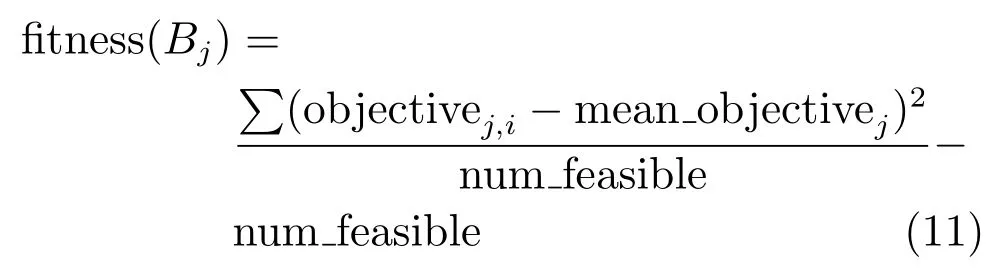

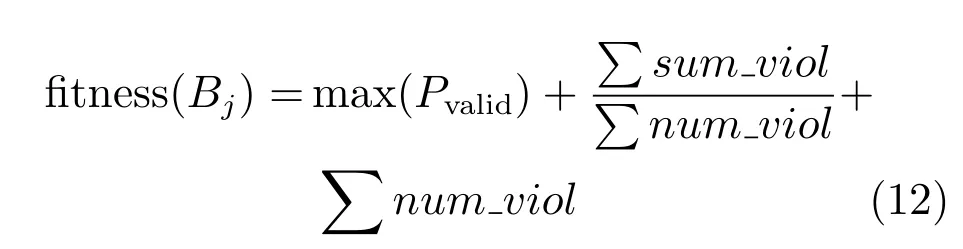
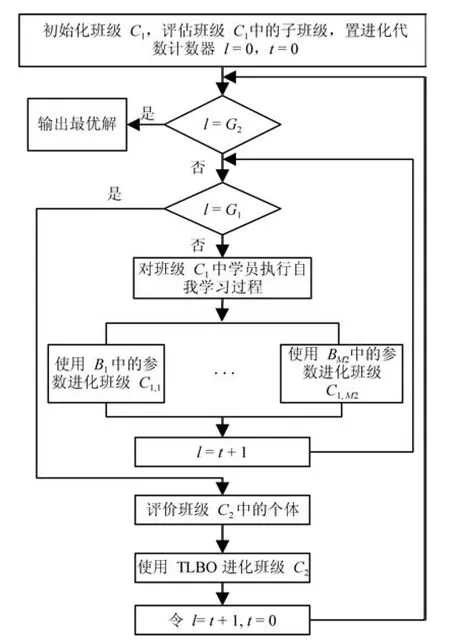
3 算法流程图
4 仿真分析
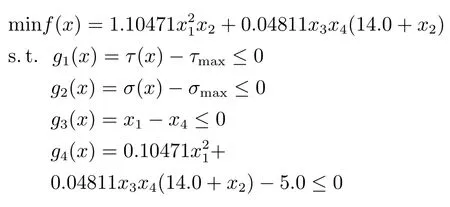

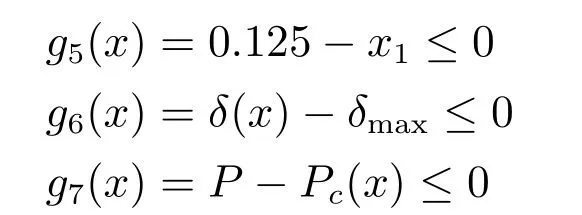




5 结论