改进模糊熵算法及其在孤独症儿童脑电分析中的应用

孙小棋 李昕 蔡二娟 康健楠

孤独症(Autism spectrum disorders,ASD)是一种复杂的关于行为和认知方面的大脑发育障碍,其特点是通过限制和固定的行为产生沟通障碍[1],主要表现为社会交往障碍、交流限制和重复性行为[2].这些疾病是高度遗传的,在兄弟姐妹间有较高的发病率[3].

与健康人相比,孤独症大脑部分皮层同步性呈现降低的现象[4].近年来脑同步性研究多集中在功能影像学、神经影像学,神经解剖学以及正电子断层扫描成像等方面.Greimel等[5]采用全脑分布形态测量技术图像显示孤独症的颞区中后叶连通性低于健康人.Kana等[6]利用磁共振技术研究孤独症的大脑连通性,发现额叶和顶叶区域之间的同步程度降低.Coben等[7]通过磁共振成像研究发现,静息状态下与健康人相比,孤独症的额叶功能连接性降低.基于影像学的方法实现脑同步性分析成本较大,且不便捷.

Duffy等[8]利用判别函数分析方法确定光谱相干因素,识别孤独症与健康脑电信号(Electroencephalogram,EEG)准确率高达97%.Lazarev等[9]基于脑电信号实现了脑同步性分析,指出孤独症头皮顶叶和中部地区的脑电信号相干系数值低于健康人.Jaime等[10]通过EMSE相干函数计算孤独症脑电信号,发现孤独症右脑颞中部的相干性低于健康人.基于脑电信号,可以分析不同脑区之间的同步性与相关性,为孤独症儿童早期发现与干预提供帮助.

熵是用来衡量大脑复杂程度的重要特征参数.雷敏等[11−12]利用样本熵和辛熵分析脑电信号发现孤独症部分脑区(前额叶、颞叶、顶叶和枕叶)的熵值低于健康人,表明孤独症儿童的行为适应性较低.Zavala等[13]以多尺度熵作为特征量,能够有效识别癫痫发作的脑电信息.Liang等[14]发现近似熵可以用于癫痫检测,实现健康人与癫痫患者发作脑电信号分类正确率在90%以上.与其他熵算法相比,模糊熵(Fuzzy entropy,FuzzyEn)有效地去除了基线漂移的影响,且向量的相似性不再由绝对幅值差确定,而由指数函数确定的模糊函数形状决定,从而将相似性度量模糊化,具有更好的抗噪声和抗干扰能力.

本文在静息状态下,采集孤独症儿童的脑电数据,基于改进模糊熵算法结合锁相位技术,分析孤独症与健康大脑复杂程度的差异性与同步性.

1 数据和方法

1.1 数据采集

数据采集使用美国Electrical Geodesics公司的EGI128导联脑电采集系统实现,采样率1000Hz.18名孤独症儿童与17名健康儿童(年龄3～9岁),家属均签署了知情同意书.试验前三天停止服用一切药物,如安眠药、用于镇静的药物等.静息状态方法不需要受试者做出反应,适合研究无法准确地执行任务的严重受损患者或年轻患者[15−16],试验记录孤独症5分钟的静息脑电信号.

本文采用均匀分布在5个头皮脑区的19个通道.这19个通道分别为额区的FP1、FP2、F3、Fz、F4,左侧颞叶的F7、T3、T5,顶叶的C3、C4、P3、Pz、P4,右侧颞叶的F8、T4、T6和枕叶的O1、Oz、O2.如图1所示,128导联EGI脑电采集系统5个相关脑区域及电极分布.基于EEGLAB工具箱完成脑电信号的预处理工作,并由滑动平均算法截取1000个数据点进行分析.

1.2 改进模糊熵

模糊熵是一种改进近似熵的非线性时间序列分析方法[17].它是基于模糊隶属函数来度量向量相似性,使用指数函数确保模糊熵的连续性和有效性.熵值不仅能够随参数变化过渡平滑,并且在参数值很小的情况下其定义仍有意义,同时继承了样本熵的相对一致性和短数据集处理特性.模糊熵需要确定r和m两个未知参数,即指数函数边界的宽度和梯度.一般情况下,过高的r和m使得边界面太宽,会导致有用信息的损失;参数过低使得边界过窄,会对噪声的敏感性增加.选择合适的参数,从而使得数据具有较好的鲁棒性.传统上,建议将r设置为0.1～0.2倍的时间序列长期标准差.但阈值r的设置是基于原始序列长期的标准差,因此无法探索真实的复杂性,忽略了各个期间时间序列的变化.而时间序列的瞬时表现更能反应脑功能状态的变化.针对这一问题,本文将r的倍数0.1～0.2等分为10个区间,计算各自对应的标准差,得到0.15倍时熵值趋于稳定,最终设置r为0.15倍一阶差分时间序列的标准差,经一阶差分计算后的数据趋于平稳,同时去除扰动和季节性的影响,最后得到能够真实反映原始数据的规律一组新序列,真正实现复杂性和时间序列的相互关系.

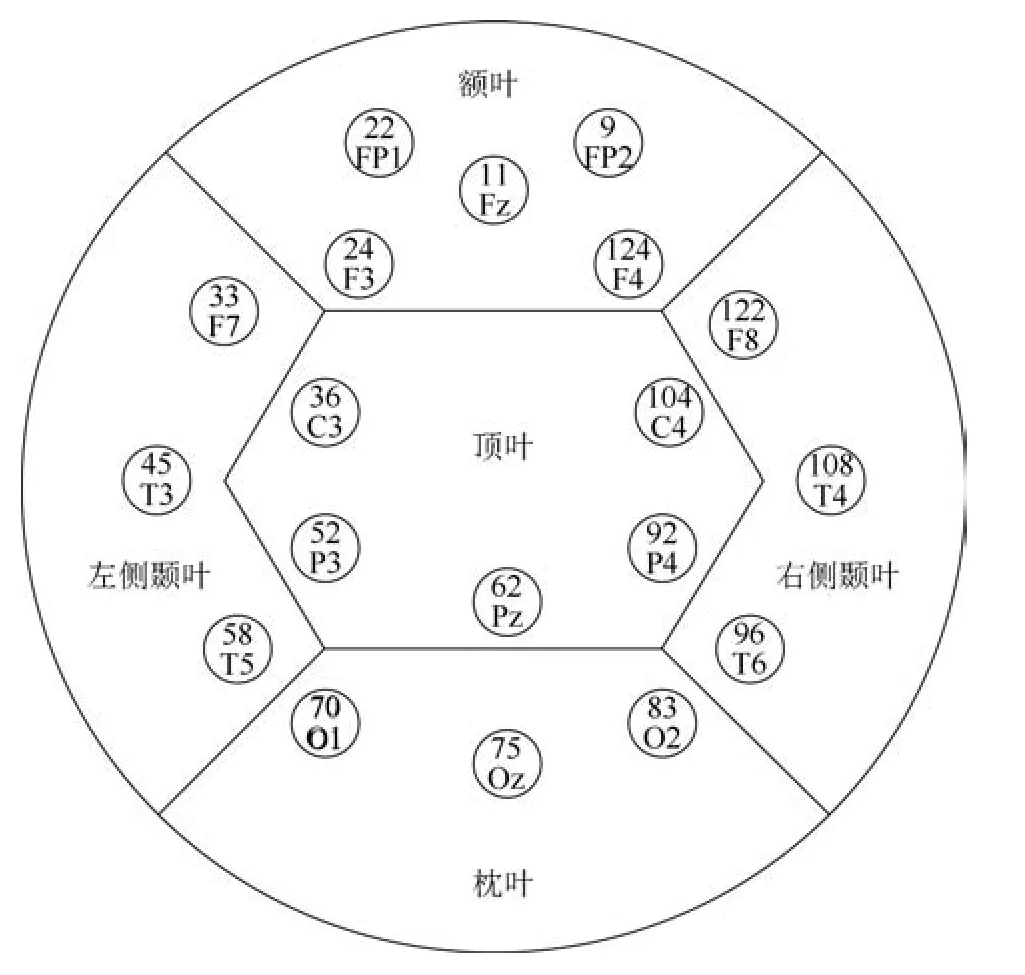
图1 EGI脑电采集系统电极分布Fig.1 The scalp electrodes distribution

改进模糊熵的算法如下:

将序列xi按顺序写成m维矢量,如式(1)所示.

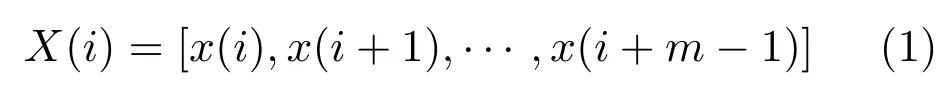
其中,i=1,2,···,N−m+1.

定义X(i)和X(j)之间的距离,如式(2)所示.

其中,k=1,2,···,m−1.

定义X(i)和X(j)的相似度,如式(3)所示.

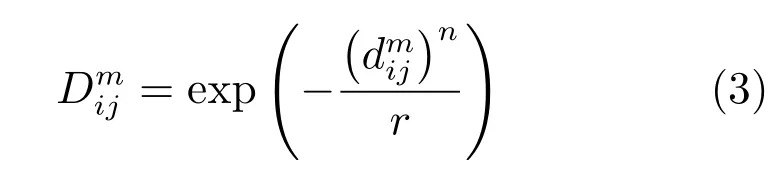
其中,n和r分别为指数函数边界的梯度和宽度.

定义r值,如式(4)～(6)所示.

其中,i=1,2,···,N.

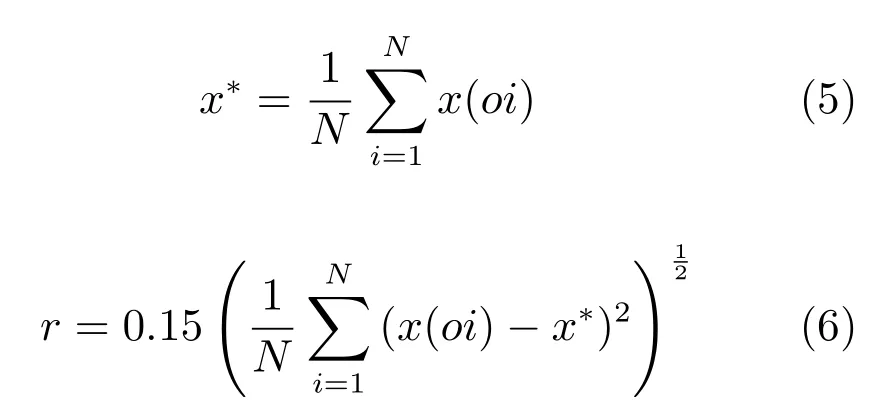
对所有i求平均值,如式(7)所示.

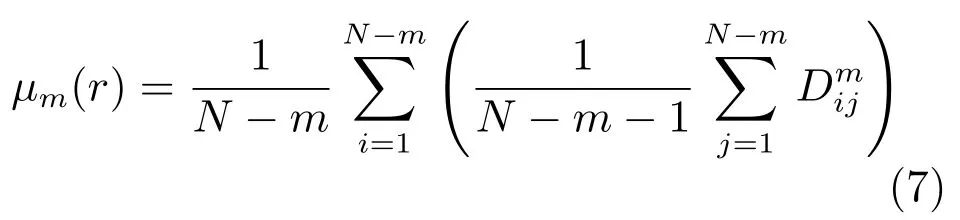
将m变为m+1,重复上述步骤即可得到模糊熵,如式(8)所示.

1.3 锁相位

锁相位是测量同步程度的一种有效方法,体现了对分布在大脑不同区域的功能以及不同脑区之间持续不断的相互作用,这种相互作用需要在有限的时间段内以及在特定的频段内通过调节神经元或者神经群并对其进行精确的锁定来完成.此外,相关研究表明,神经振荡的频率是影响孤独症大脑皮层连接性的一个重要因素[18].脑电通常分为4种基本的节律波:Alpha波(8～12Hz)、Beta波 (12～30Hz)、Delta波 (0.1～3Hz)、Theta波(4～7Hz).其中,Alpha波和Beta波处于清醒状态呈现的脑电节律[19],Delta波和Theta波处于意识减弱甚至无意识状态呈现的脑电节律.本文因此选择Alpha波和Beta波进行数据分析,其步骤如下:

1)信号经经验模态分解(Empirical mode decomposition,EMD)得到多个固有模态函数(Intrinsic mode function,IMF)分量[20];

2)选取Alpha和Beta节律波所在频率的IMF分量,作为希尔伯特变换的输入时间序列;针对该敏感IMF分量进行希尔伯特变换得到瞬时幅值;

3)计算锁相位的值,如式(9)所示.

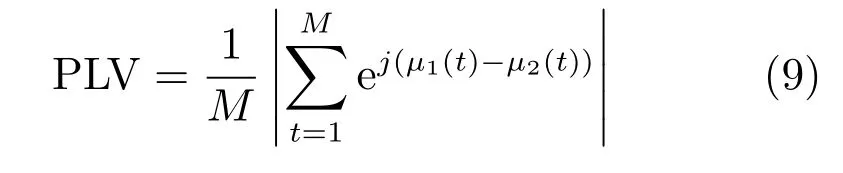
由式(9)可知,锁相位的取值范围为[0,1],并且仅对相位的瞬时值敏感.锁相位反应了两个信号相位的波动情况,若两个信号瞬时相位差值小,即相位变化小甚至没有区别,那么锁相位接近于或者等于1,若两个信号瞬时相位差值大,即相位波动大,那么锁相位趋近于0.

1.4 相关向量机

2001年,Tipping[21]基于稀疏贝叶斯理论提出了一种核函数算法—相关向量机(Relevance vector machine,RVM),用于处理回归和分类问题.RVM算法采取全概率框架,将先验概率引入到模型权重上.超参数与权重之间一对一的支配,通过反复迭代数据获得超参数的值.在实际应用中,大部分的超参数趋于无穷,相应的权值近似于零,由此说明RVM模型是稀疏的.根据自相关判定原理,与少数不为零的权值相关的训练向量被称为相关向量.

对于二分类问题,设训练样本的集合为xi,tiN,其中xiN为特征值,tiN是相应的目标值,N为训练样本数,二分类问题时目标值只可能为0或1.RVM的分类函数定义,如式(10)所示.

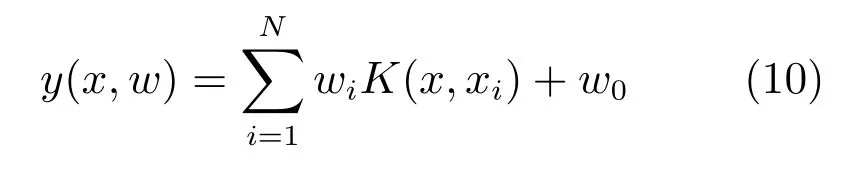
若所有观测样本之间是相互独立的,由伯努利分布可求得输出目标值t的似然估计概率,如式(12)所示

其中,w=[w0,w1,···,wN]T.

在贝叶斯框架下,权值w可以通过极大似然法获得,但为避免过学习现象,RVM为每个权值定义了高斯先验概率分布来约束参数,如式(13)所示.

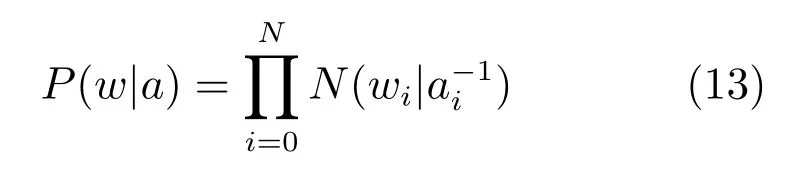
其中,a为N+1维超参数.

由于式(12)不是正态分布函数,不能直接通过求定积分来确定权重的大小.因此,本文采用Tipping提出的拉普拉斯逼近法[21],反复更新a和σ2的值,若达到最大迭代次数或满足收敛条件则停止计算.根据得到测试点的概率预测值p(t=1|x∗)和p(t=0|x∗)的大小,最终确定x∗最优可能的所属类别.

2 脑电信号分析

2.1 统计分析

试验采集了18名孤独症儿童和17名健康儿童的脑电数据,基于锁相位与改进模糊熵算法(如图2所示),分析孤独症大脑同步性与复杂程度,进而确定孤独症的敏感脑区.

在《论语·雍也》中，孔子表扬了一个叫孟之反的人。孔子表扬他什么？“不伐”。“伐”在古汉语中是“夸耀”的意思，“不伐”，就是“不自矜”。这与《史记》中司马迁评价项羽恰相反。司马迁说项羽“自矜功伐，奋其私智而不师古”，这大约就是项羽失败的原因。

基于SPSS统计分析,分别对传统模糊熵和改进模糊熵值进行t检验.改进模糊熵值统计结果表明,孤独症与健康人之间的脑电信号复杂程度存在显著差异(P<0.05).

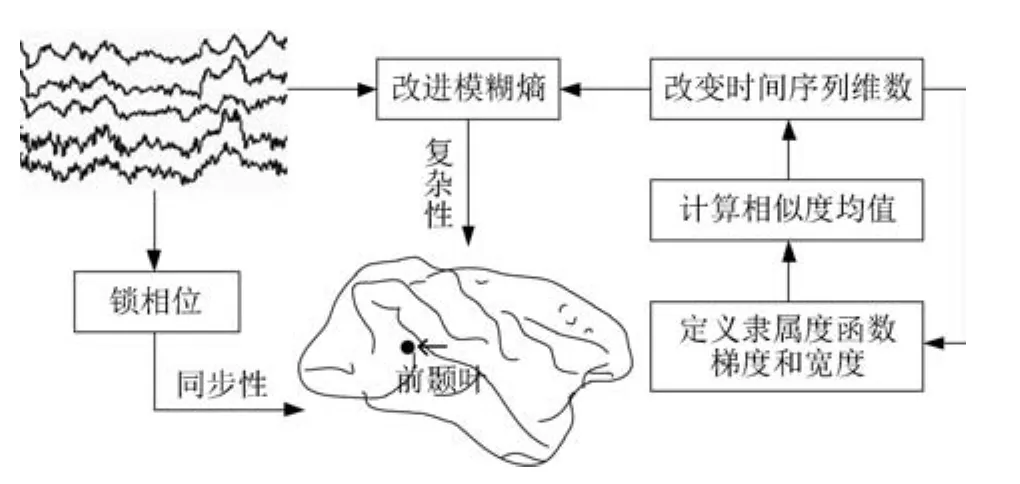
图2 整体框图Fig.2 Block diagram

2.2 分类对比

依据传统模糊熵与改进模糊熵算法,分别提取孤独症和健康人的特征值,采用10倍交叉验证,利用RVM 对比两种特征向量的分类准确率,如表1所示.

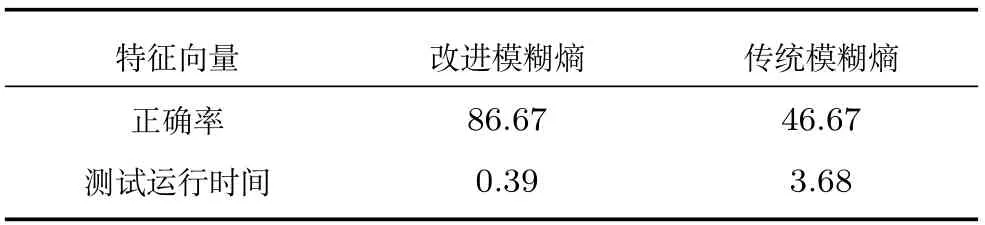
表1 两种特征获得的识别率Table 1 The classification accuracy obtained by__________________different features

由表1可知,孤独症与健康脑电信号识别时,分类效果差异很大.由此说明特征指标选择是否合适不仅是影响分类器运行时间长短的一个重要原因,也是关乎识别效果的关键因素.基于改进模糊熵算法,获得分类正确率与测试运行时间分别为86.67%、0.39秒.传统模糊熵作为特征指标进行分类识别时仅为46.67%,运行时间为3.68秒.改进模糊熵算法不仅降低了运算时间,分类正确率也显著提高.

2.3 基于改进模糊熵的脑复杂度分析

孤独症是由于神经系统失调导致的发育性障碍,大脑神经元处理信息活动的有序程度降低,部分大脑区域复杂程度下降.基于改进模糊熵算法,提取额叶、顶前叶、前颞叶和枕叶的脑电数据特征信息,观察孤独症和正常脑电信号熵值变化情况,如图3所示.

由图3可知,基于改进模糊熵算法计算大脑复杂性,孤独症的F7、F8和P3、P4四个导联的熵值明显低于正常的熵值,说明前颞叶和后顶叶可以作为区分孤独症的有效脑区.而其他导联与健康人相比,呈现出不同高低变化的熵值,例如,额叶的F3通道孤独症的熵值低于正常的熵值,F4通道孤独症的熵值却高于正常的熵值,故不作分析.

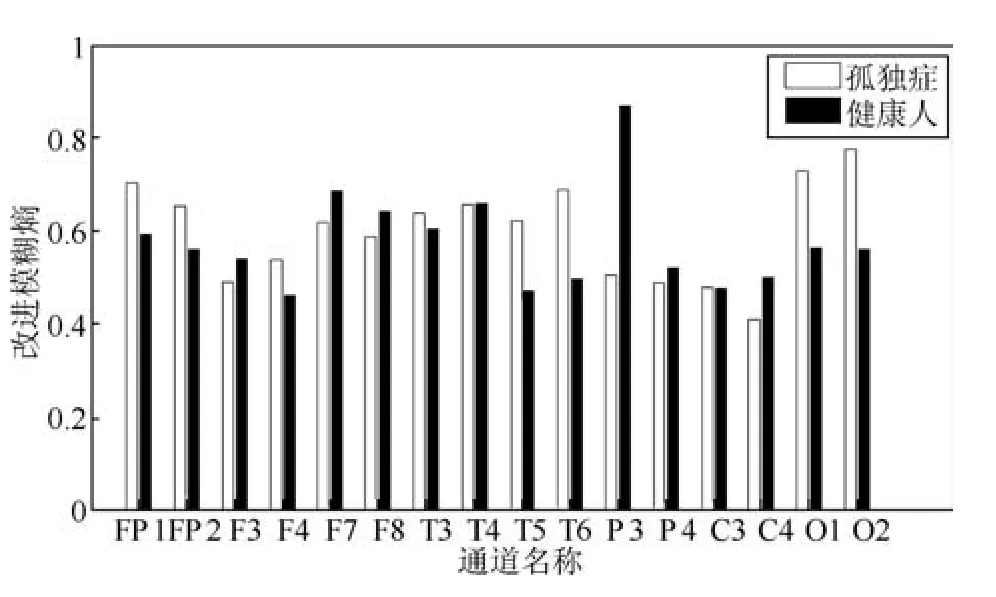
图3 改进模糊熵值Fig.3 Improved fuzzy entropy

2.4 基于锁相位同步性分析

基于改进模糊熵分析结果,前颞叶存在较明显的低复杂度,再进一步作同步性分析.以受试者的16个通道脑电信号的锁相值作为检查变量,分为孤独症和健康人共两组,采用SPSS进行t检验,孤独症和健康人之间的差异较为明显(P=0.048<0.05),绘制孤独症和正常的互锁相位,如图4所示.

从图4中可以看出,孤独症和正常的互锁值随电极对分布的变化情况.与健康人睁眼相比,孤独症额区(FP1、FP2、F3、F4)互锁相位值较小;前颞叶(F7、F8)互锁相位值较小,中颞叶(T3、T4)和后颞叶(T5、T6)互锁相位值较大;前顶叶(C3、C4)互锁相位值较小,后顶叶(P3、P4)互锁相位值较大;枕叶(O1、O2)互锁相位值较小.表明孤独症的额叶、前顶叶、前颞叶和枕叶区域的大脑同步性降低.以往也有相关研究,如Coben等[7]利用核磁共振技术发现孤独症额叶的相干性低于健康人.Lazarev等[9]指出与健康人相比,孤独症的头皮顶叶和中部地区的脑电相干性下降.Jaime等[10]通过EMSE相干函数发现孤独症脑电相干性的敏感脑区位于中后颞叶.

图4 电极互锁相位Fig.4 Phase interlocking value

3 讨论

相比影像学方法,基于脑电信号分析孤独症的脑复杂性与同步性,具有成本低[22−23]、结果更鲜明等优点.本文结合改进模糊熵和锁相位作为特征参数,着重分析了孤独症和正常的脑电信号差异,得到了较好的效果.

模糊熵用于衡量信号产生新模式的概率,与不规则程度呈正比关系,熵值越大,信号的复杂性越强.基于改进模糊熵算法,发现孤独症前颞叶和后顶叶的脑电信号熵值较低,所呈现出的复杂性明显低于正常.这一结果表明,孤独症与健康脑电信号之间存在差异性,且不同脑区敏感程度不同.

在分析脑复杂程度基础上,本文利用锁相位方法分析了孤独症的脑电信号相干性,结果显示孤独症的额叶、前顶叶、前颞叶和枕叶区域的大脑同步性降低.进一步,综合复杂性与相关性分析结果表明,孤独症前颞叶的大脑复杂性和同步性均低于正常,前颞叶可以作为评估孤独症的一个重要脑区.

前额叶皮层与执行控制和问题行为具有直接的相关性,通常人体的注意力、社会交往和情感问题大都与前额叶皮层相关[24−25].而孤独症临床多表现为严重的社交障碍,语言匮乏,因此,大多数学者分析主要集中于孤独症的前额叶问题[26−28].虽然也有一些研究指出,孤独症的敏感脑区位于颞叶[5]和顶叶[29],但相关脑区的研究尚不多见.本文基于模糊熵算法提出了一种改进的时间序列度量方法,能够有效评估复杂程度,更加完整、充分地反映脑功能状态.发现孤独症脑电信号复杂性降低和同步性下降,确定了孤独症的敏感脑区—前颞叶.研究表明,前颞叶为精神皮质,人类的情绪和精神活动与其关联.结合前颞叶与前额叶的脑电相关分析,能够更好地体现孤独症的大脑活动信息,为孤独症的分析提供帮助.

4 结论

为了保证充分提取时间序列瞬时复杂性特征,本文提出了一种改进模糊熵算法.通过改进算法分析孤独症儿童脑电信号特点,与传统算法相比,改进算法运行时间相对减少,大大提高了识别效果.进一步,结合改进算法与锁相位分析孤独症儿童不同脑区的复杂性与同步性,结果表明:孤独症患者前颞叶的脑电信号同步性下降、复杂性降低,具有显著性差异(P<0.05).同时分析了孤独症敏感脑区,为以后的研究提供参考.