自适应遗传算法的改进与应用*

张国强 彭晓明

(空军雷达学院研究生管理大队1) 武汉 430019)(空军雷达学院预警监视情报系2) 武汉 430019)

1 引言

自适应遗传算法是具有比例选择,自适应交叉和变异操作的遗传算法的简称。针对不同的优化问题,简单遗传算法和一些改进的遗传算法的交叉概率和变异概率需要反复用实验来确定,而且不容易找到适用于所有问题的最佳值。而自适应遗传算法的交叉概率和变异概率是随适应度自动改变的,此方法能够采用相对某个解的最佳交叉概率和变异概率。自适应遗传算法不但能维持种群的多样性,而且还保证了遗传算法的收敛性[1]。

自适应遗传算法的缺点[2]:自适应遗传算法比较适用于进化的后期,对于进化的初期很不利。因为在进化初期,一些适应度较好的个体会处于一种几乎不变化的状态,从而导致种群中的其它个体很快被淘汰,加快了种群的收敛速度,但种群却很难收敛到全局最优解,最终出现早熟收敛。

2 自适应遗传算法的改进

1994年,Srinivas等人提出了一种根据适应度动态调整交叉概率Pc和变异概率Pm的自适应遗传算法(Adaptive Genetic Algorithm,AGA)[3]。在 AGA算法中,交叉概率和变异概率随着个体的适应度在种群平均适应度和最大适应度之间进行线性调整。当适应度越接近最大适应度时,交叉概率和变异概率越小;当适应度值接近或等于最大适应度值的个体时,交叉概率和变异概率接近或等于零。

任子武等人在Srinivas等提出的自适应遗传算法的基础上,提出一种改进的自适应遗传算法(Improved Adaptive Genetic Algorithm,IA-GA)[4]。IAGA算法为了保证每一代的优良个体不被破坏,采用了精英保留策略,即如果下一代种群的最优个体适应度值小于当前种群最优个体适应度值,则将当前种群最优个体或者适应度值大于下一代最优个体适应度值的多个个体直接复制到一代,随机替代或替代最差的下一代种群中的相应数量的个体。精英保留策略保证了当前的最优个体不会被交叉、变异等遗传操作破坏。在IAGA算法中,交叉概率Pc和变异概率Pm按如下公式进行自适应调整。

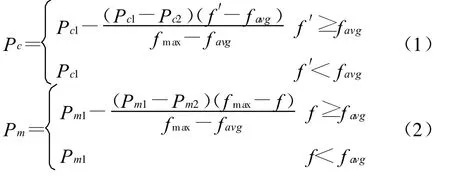
在AGA算法中,当适应度值等于最大适应度值的时候,交叉概率和变异概率的值为零,容易产生局部最优解;在IAGA算法中,较差个体的变异能力较低,容易产生停滞现象。而精英保留策略虽然起到了保护和推广优秀个体的作用,但是其个体数目不宜过大,否则会使种群进化陷入停滞不前,造成局部收敛[5]。

为了克服这两种自适应遗传算法的不足之处,本文在Srinivas等人提出的AGA算法的基础上,结合任子武等人提出的IAGA算法,对自适应遗传算法的交叉概率和变异概率进行改进,提出了根据适应度值来动态调整交叉概率和变异概率的一种新的自适应遗传算法(New Adaptive Genetic Algorithm,NAGA)。交叉概率Pc和变异概率Pm按如下公式进行自适应调整。

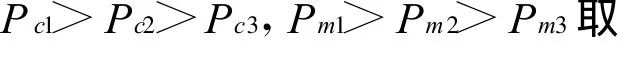
因此,根据本文提出的新的自适应遗传算法的交叉概率和变异概率的公式,可以得出交叉概率Pc和变异概率Pm随适应度值的变化情况,如图1所示。

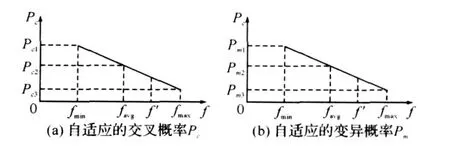
图1 NAGA算法自适应交叉概率和变异概率

本文提出的改进的交叉概率和变异概率,是根据适应度值的集中程度,以种群为单位,自适应地变化整个种群的交叉概率Pc和变异概率Pm,采用种群的最大适应度值 fmax,最小适应度值 fmin和平均适应度值 favg这三个变量来衡量种群适应度值的集中程度。使交叉概率Pc和变异概率Pm随着个体的适应度值在种群的最小适应度、平均适应度和最大适应度之间进行调整。

由式(1)可知,当要交叉的两个个体中较大的适应度值大于或等于平均适应度值时的自适应调整公式以及当要交叉的两个个体中较大的适应度值小于平均适应度值时,则认为交叉概率Pc等于指定值。而本文的改进的交叉概率要随着个体的适应度值在种群的最小适应度、平均适应度和最大适应度之间进行调整。当要交叉的两个个体中较大的适应度值小于平均适应度值时,要交叉的两个个体中较大的适应度值应该在最小适应度值和平均适应度值之间调整。由此得到本文的交叉概率Pc式(3)。同理由式(2)得到变异概率Pm式(4)。

改进后的交叉概率和变异概率不但能够随适应度自动改变,而且使种群中最大适应度值的个体的交叉概率和变异概率不为零,这就相应地提高了种群中表现优良的个体的交叉概率和变异概率,使得它们不会处于一种近似停滞不前的状态,从而使算法跳出局部最优解。将个体的适应度与当代种群的平均适应度进行比较,在种群演化中有效地保留了优秀个体的模式,增强了较差个体的变异能力,使算法能跳出局部最优解,克服早熟的缺点。

3 仿真实验分析

为了比较本文算法(NAGA算法)的收敛速度,选取一个简单的单峰值函数(DeJong球函数)进行实验。将NAGA算法与AGA算法以及IAGA算法的独立实验结果进行比较。待优化的函数为:

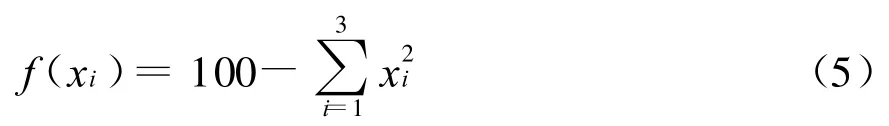
其中,x∈[-5.12,+5.12],此问题为极大值问题,该函数的极大值在(0,0,0)处为100。将各算法分别独立实验30次的结果平均值记录于表中,则实验结果比较如表1所示。

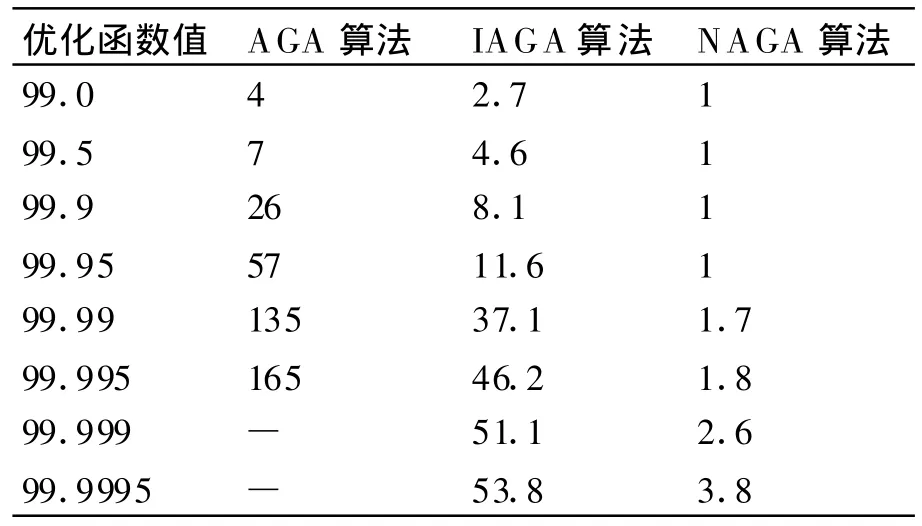
表1 各种遗传算法达到指定函数值的平均进化代数比较表

由表1中的数据可以发现,NAGA算法在收敛速度上有了明显提高。AGA算产生了实验结果不收敛的现象;IAGA算法虽然没有产生实验结果不收敛的现象,但是可以看出,当优化函数值接近最优值100时,NAGA算法在30次实验中的平均进化代数为3.8,其实验结果明显优于其它两种算法因此,从表1的实验结果比较可知,NAGA算法不仅具有较快的收敛速度,而且能得到更优越的解,它的性能比简单遗传算法和现有的一些自适应遗传算法均有一定改善。

4 结语

全局优化和快速收敛本来就是相互矛盾的,一种较好的算法就要综合考虑全局优化和快速收敛,选择一种实际效果较好的方法实验结果表明,本文提出的改进的自适应遗传算法(NAGA算法)在提高收敛性能的同时,基本保持了遗传算法的运算速度,在快速收敛和全局最优之间获得了较好的平衡,从而保证了种群能够快速协调地进化。

[1]Wang Hongjian,Zhao Jie,Bian Xinqian,et al.An improved path planner based on adaptive genetic algorithm for autonomous underwater vehicle[C]∥Proceedings of the IEEE International Conference on Mechatronics and Automation,2005,2:857～861

[2]王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002:9,14～15,25～28,68

[3]SRINIVAS M,PATNAILK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE T ransaction on System,Man and Cybernetics,1994,24(4):656～667

[4]任子武,伞冶.自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报,2006,18(1):41～66

[5]黄康,许志伟,董迎晖.改进的遗传算法及其在多目标优化设计中的应用[J].机械设计,2005,22(9):735～738