基于滑模观测器和广义观测器的故障估计方法

文传博 邓露 吴兰

随着科学技术的飞速发展,控制系统变得日益复杂,各类故障时常发生.无论执行器故障还是传感器故障都将影响系统的性能,甚至导致系统的不稳定,进而引发严重的安全事故.为了增加系统的可靠性,及时做出故障诊断就显得尤为重要[1−3].相较于故障检测和隔离,故障估计直接获得故障的幅值,还可为进一步实现故障调节和容错控制服务.因此故障估计更具有实际意义,但同时困难也大.故障估计的众多技术中,基于各类观测器的估计方法受到研究人员的青睐,取得了丰富的研究成果[4−5].

当执行器发生故障时,文献[6]依次研究了正常系统和不确定系统的故障估计问题,提出了相应的自适应观测器,还通过调整参数增强了算法的鲁棒性.针对多输入多输出系统的执行器故障,文献[7]利用降阶的卡尔曼滤波器联合估计了系统状态和故障,并设计控制器消除故障带来的影响.在此基础上,文献[8]进一步研究了非线性广义系统执行器故障的鲁棒估计和故障容错问题.针对一类不满足利普希茨条件的非线性不确定系统,文献[9]通过解一组线性矩阵不等式和设计多个滑模观测器依次实现了故障检测、隔离和估计.滑模观测器同样被应用在一类线性时变系统的执行器故障估计中,其中设计的观测器增益包含了干扰矩阵的信息,从而保证了观测器的稳定性[10−11].

当传感器发生故障时,通常将传感器故障转化为伪执行器故障,再利用已有的方法实现重构[2,12−15].例如,文献[2]提出的两种方法均是将传感器故障转化为执行器故障,再分别设计滑模观测器得到故障的估计值,并论证观测器存在的充分条件.文献[12]首先设计执行器故障的滑模观测器,而后通过系统变换,用类似的方法解决了传感器故障的重构问题,并将结果进一步推广到广义系统.文献[13]针对一类非线性系统,研究了传感器故障、系统噪声和输出噪声同时存在时的故障估计问题,得到了系统状态和传感器故障的联合估计值.通过将系统解耦为两个子系统,文献[14]实现了一类不确定系统的故障观测器设计,并将系统稳定性的问题转化为求解一个线性矩阵不等式问题.文献[15]设计了同时实现状态与执行器故障联合估计的未知输入观测器,并将其应用到传感器故障诊断中.

实际应用中,系统的故障往往并非单独发生的,更多的是出现执行器和传感器并发故障,还时常受未知干扰的干扰.对于这类故障,文献[16]针对一类非线性系统设计了同时实现两类故障估计的观测器,但未考虑外界干扰带来的影响.文献[17]对于受缓变干扰影响的系统,给出了干扰的自适应估计方法,在此基础上重构了干扰和传感器故障,但该方法对故障的形式有严格的限制.文献[18]进一步研究了含有执行器故障、传感器故障且受未知干扰系统的故障重构问题,利用滑模抵消干扰的影响,估计了传感器故障,但只能实现执行器故障的检测,却无法重构.因此,能同时估计执行器故障和传感器故障及干扰的方法,有待进一步的研究.

本文针对一类同时存在执行器故障、传感器故障和未知干扰的非线性系统,开展故障估计的研究.首先,利用非奇异变换将原系统转化为两个降阶的子系统;然后,设计广义观测器方法估计部分状态变量及传感器故障,同时给出干扰的自适应估计算法;接着设计带干扰补偿的滑模观测器,结合等效输出控制原理重构执行器故障;最后,用计算机仿真验证本文算法的有效性.

1 模型描述

考虑如下的非线性系统:

假设1.系统(A,D,C)满足:

假设2.系统(A,M,C)满足:

引理1[3].对于故障系统(1)和(2),若假设1的式(3)成立,则存在非奇异变换矩阵T和S,使得:

子系统1:

2 观测器设计

在第1节解耦所得两个降阶系统的基础上,本节将分别设计广义观测器和滑模观测器,在得到系统状态以及未知干扰的估计值,为下节重构执行器和传感器故障做准备.

对子系统(13),(14)和(11),(12)分别设计观测器:

注1.假设3中的式(15)和秩条件rank(C1D1)=rank(D1)是子系统1滑模观测器存在的条件[1].而由rank(CD)=,可知式(3)保证了该条件的成立。

注2.式(31)中可检测时,可配置极点使误差稳定,即其满足:

上式成立的充要条件是(A4,C4)可检测[16],即(A,C)可检测[22],式(4)保证了误差动态系统(31)的稳定.

注3.在出现执行器和传感器并发故障时,文献[3]用H∞方法处理未知干扰,最小化干扰对故障重构误差的影响,但不能估计出干扰,文献[17]构造的估计器只含估计误差的纯积分项,仅对定值或缓变干扰有效,但实际应用中突变干扰更常见.为此,我们引入了误差项的比例项,如式(22)所示,有助于改善观测器的快速性,进一步消除了未知干扰对状态估计误差的影响.

3 故障估计

观测器(20)～(22)得到了系统状态和干扰的估计值,在此基础上,本节依次给出执行器故障和传感器故障的估计方法.

3.1 执行器故障重构

当故障存在时,为使状态误差(26)的滑模运动在有限时间内到达并维持在滑模面S上,我们将设计滑模项的增益ρ0.根据式(23),定义滑模面为:

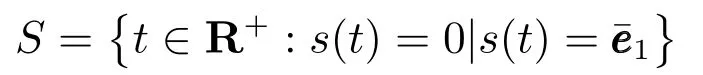
定理 2.对子系统式(13)设计观测器(18)和(19),滑模项为(23),当式(25)有解时,误差有界,若增益ρ0满足:

其中,η0为任意的较小正标量,则状态估计误差(26)将在有限时间内到达并维持在滑模面上.

证明.由定理1,收敛到,其中

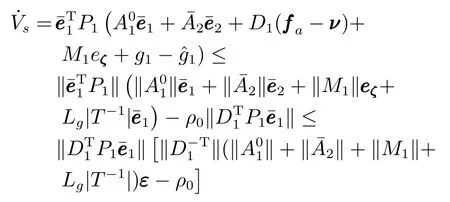
其中,veq为不连续项的等效输出控制信号,维持滑模运动,因此

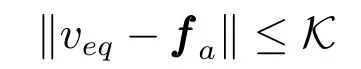
当K足够小时,可以得到:

其中,δ为较小的正标量,用以减小滑模运动的抖振.

3.2 传感器故障估计

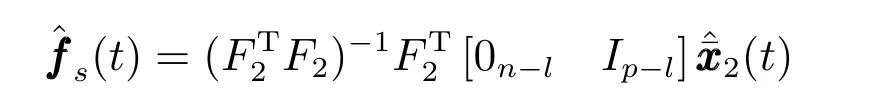
由式(45)代入式(31):

4 计算机仿真

本节通过计算机仿真验证算法的有效性.考虑同时发生传感器故障和执行器故障的系统(1)和(2),其中参数为

执行器故障、传感器故障和干扰函数分别为

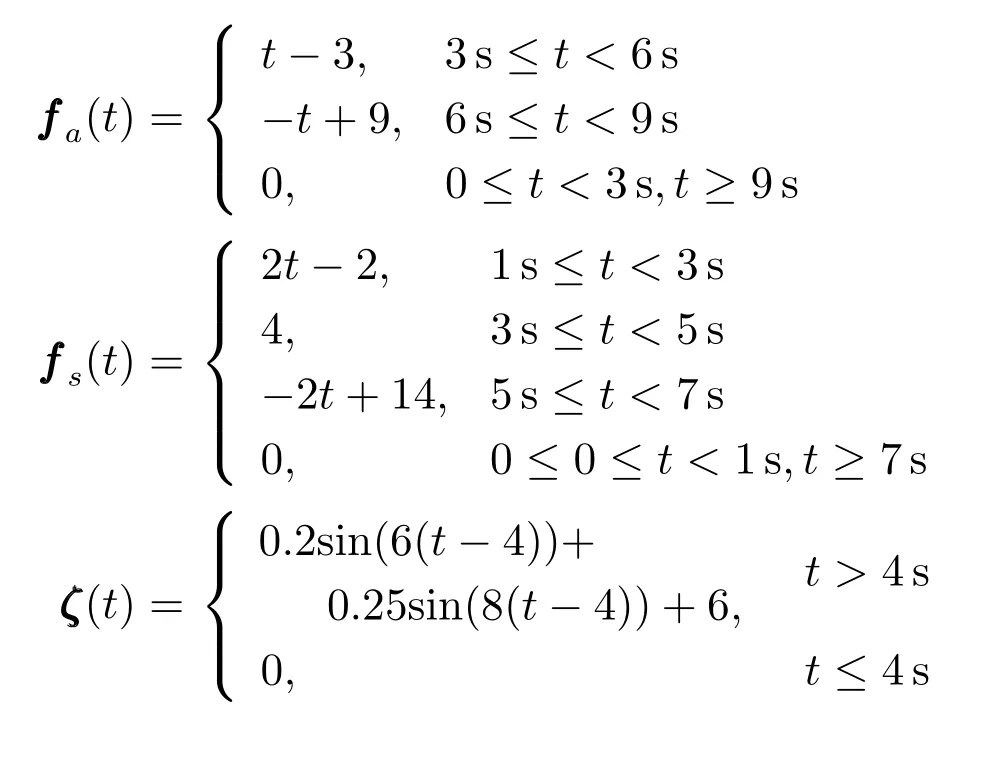
根据文献[8]中线性变换矩阵的求法,求得引理1中矩阵T、S:

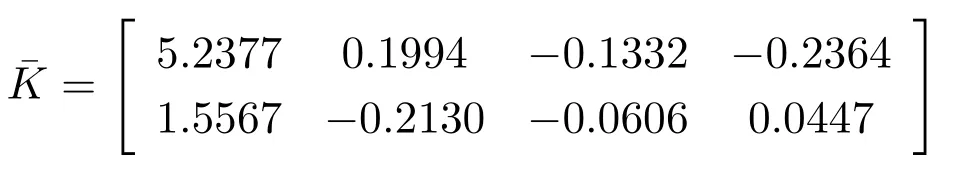
根据引理4求得K1=0.2,K2=[1−3],再求解式(24)得:

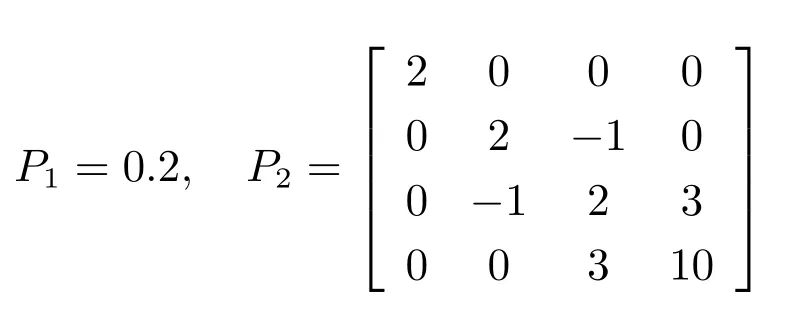
图1～3显示了该类观测器对状态变量的估计.从图中可以看出除了初始阶段之外,观测器对系统状态的三个变量都有较好的估计.图4为传感器故障的实际值与估计值曲线,可以看出估计值在第1s至第7s之间明显偏离了0,能跟踪故障的真实值,但存在一定的延迟.

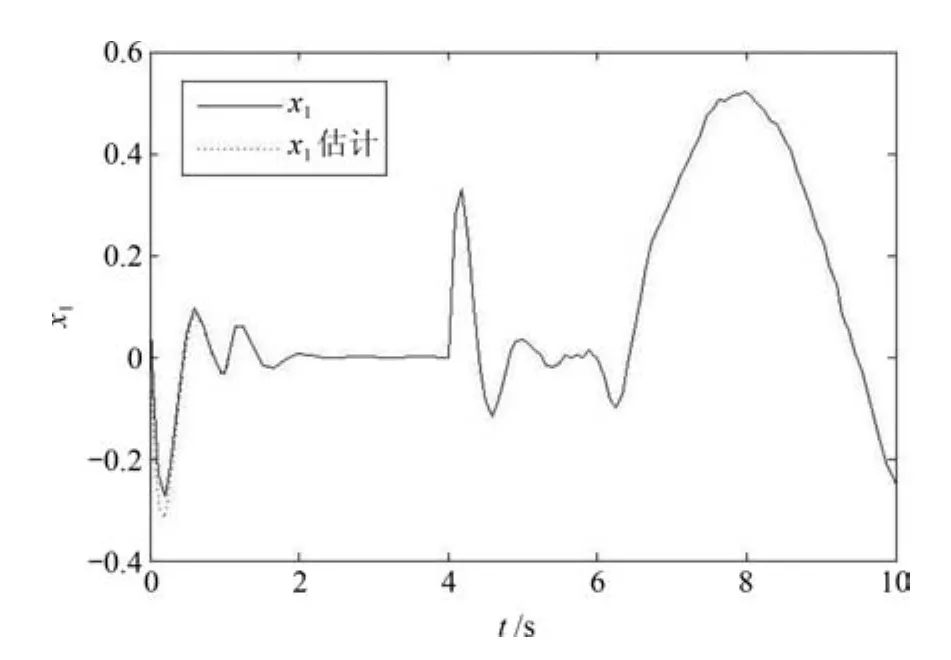
图1 状态x1的真实值与估计值Fig.1 The actual state and the estimate ofx1

图2 状态x2的真实值与估计值Fig.2 The actual state and the estimate ofx2

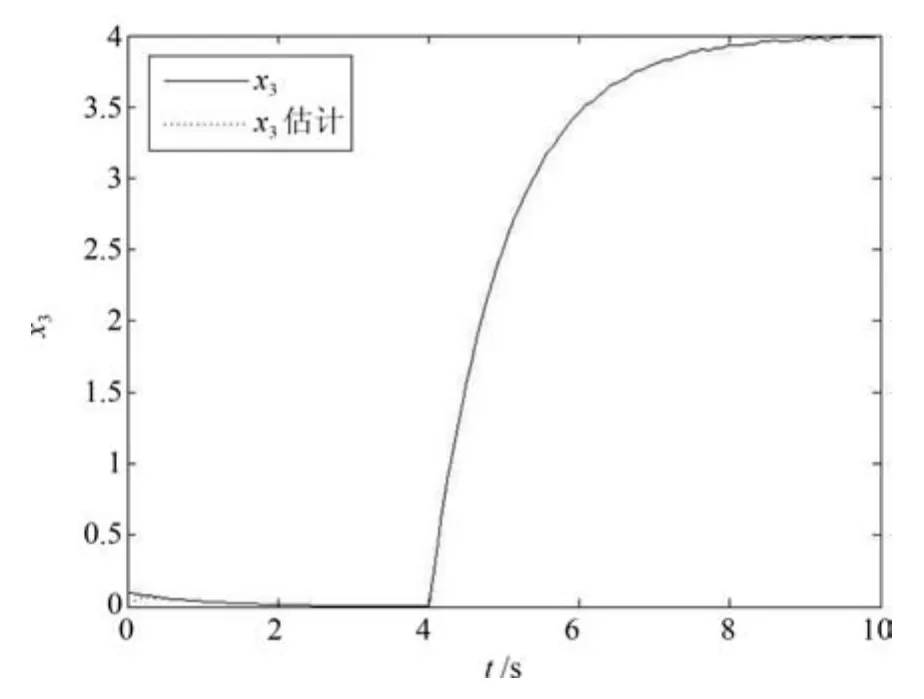
图3 状态x3的真实值与估计值Fig.3 The actual state and the estimate ofx3

图5为未知干扰的真实曲线与估计曲线,为了说明对干扰估计的效果,我们还给出了利用文献[17]得到的估计曲线.从图5中可以看出,本文方法的估计效果更好,这是由于该方法中增加了误差比例项,有效地提升估计的快速性,估计效果有明显改善,为执行器故障的精确重构提供了保障.

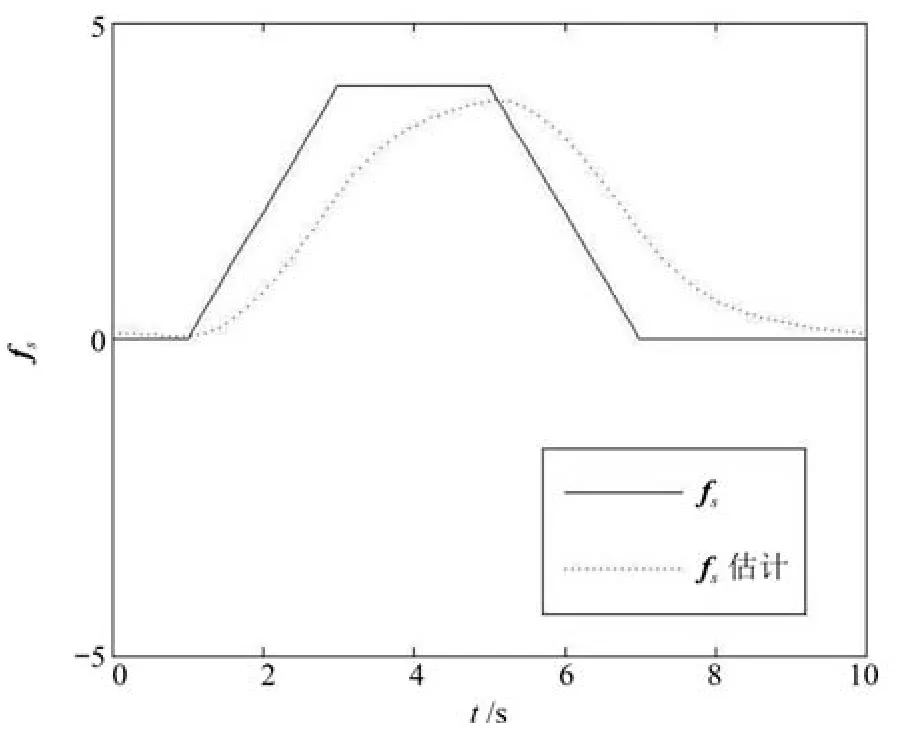
图4 故障fs的真实值与估计值Fig.4 The actual state and the estimate of faultfs

图5 干扰ζ的真实值与估计值Fig.5 The actual state and the estimate of disturbanceζ

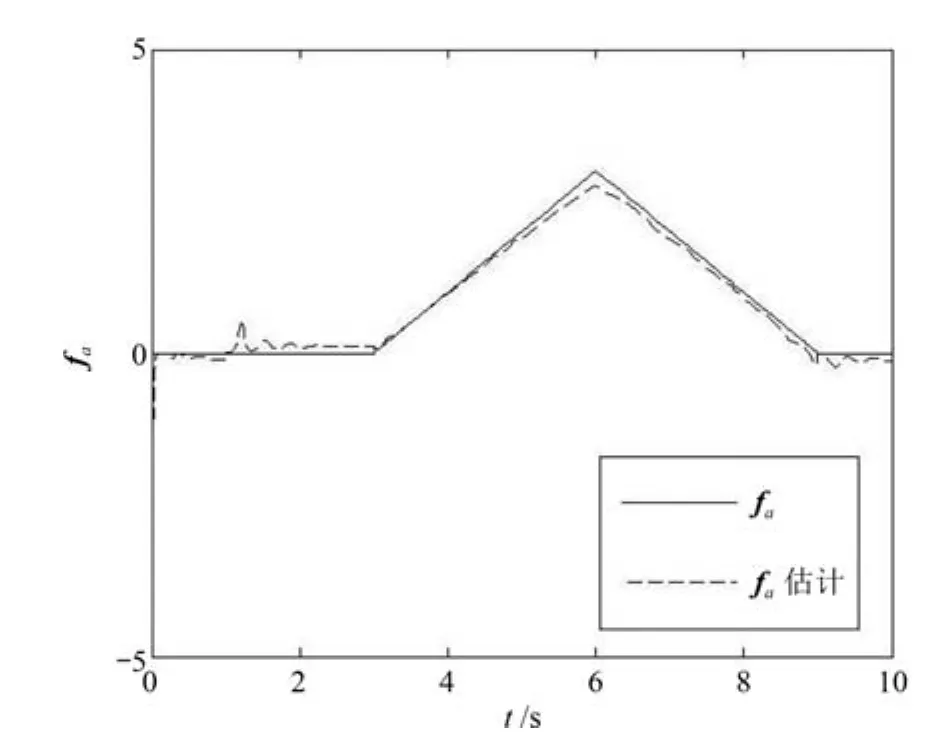
图6 故障fa的真实值与估计值Fig.6 The actual state and the estimate of faultfa

图6给出了执行器故障的估计曲线,其中ρ取15,δ取0.01.可以看出,在初始阶段估计值有抖动,在第3s故障发生之后,估计值能较好地跟踪故障真实值,说明了滑模观测器的有效性.

5 结论

本文针对非线性系统的执行器故障和传感器故障,提出了一种基于广义观测器和滑模观测器的估计方法.利用系统变换,将执行器故障和传感器故障分别解耦在两个子系统中,然后设计广义观测器和滑模观测器估计系统状态和干扰,在此基础上,根据等效输出控制原理重构了执行器故障,利用广义观测器的估计结果得到了传感器故障的估计值,并探讨了通过调整观测器增益来降低故障对系统负面影响的方法.需要指出的是,本文所研究系统的参数要求满足一些的假设条件,所提方法的应用范围受到了一定的限制,接下来,我们将研究更一般系统的故障估计问题.