基于未知输入集员滤波器的不确定系统故障诊断

汤文涛 王振华 王烨 沈毅

安全性和可靠性对于很多工程系统至关重要,例如飞行器控制系统、化工系统和核电系统,这类系统一旦发生故障,可能会造成重大的财产损失和人员伤亡_[1].故障诊断技术是提高系统安全性和可靠性的有效途径,受到了国内外学者的广泛关注.故障诊断方法通常可以分为基于模型的方法、基于知识的方法和基于信号处理的方法.其中基于模型的故障诊断被研究得最为深入,出现了基于观测器的故障诊断、基于等价空间的故障诊断、基于滤波器的故障诊断、基于参数估计的故障诊断等很多较为成熟的方法[2].由于建模误差和模型参数不确定性的存在,系统模型不能准确描述实际系统的行为,而且实际系统中广泛存在噪声和未知干扰[3],这会降低基于模型的故障诊断的效果,因此鲁棒性成为基于模型的故障诊断的重要指标.文献[4]针对存在模型误差和未知干扰的线性系统,提出了一种自适应诊断方法,可以得到故障的鲁棒估计.文献[5]基于一组H−/H∞未知输入观测器进行鲁棒故障诊断.目前对参数不确定性的处理仍然是基于模型的故障诊断的一个难题,这方面的研究成果较少.文献[6]针对存在模型参数不确定性和未知输入的线性不确定系统,设计了鲁棒故障检测滤波器.文献[7]进一步研究了线性不确定系统鲁棒故障检测滤波器和反馈控制器的集成设计问题.

传统基于模型的故障诊断方法大部分都假设噪声和干扰符合一定的概率分布,例如基于滤波器的故障诊断一般假设噪声和干扰符合高斯分布,然而很多实际系统关于噪声和干扰的概率分布的先验知识一般很难得到.集员估计只假设系统的干扰和噪声是未知但有界的,这一点在很多实际系统中都可以得到保证[8].集员估计的目标是得到与系统模型、测量数据以及干扰和噪声相容的状态或参数的可行集,一般情况下可行集的范围很难精确描述,因此集员估计往往寻找能够包含可行集的简单几何体来近似可行集,常用的几何体包括区间、椭球、平行多面体、普通多面体、全对称多胞形(Zonotope).其中基于椭球的集员滤波被研究得最多,国外学者在这方面已经取得了很多研究成果,国内学者也对基于椭球的集员滤波算法进行了研究[9−11].但是基于区间、椭球、平行多面体的方法近似保守性较大,而普通多面体的计算复杂度会随着多面体维数增大而指数增加[12].基于全对称多胞形的集员滤波能够转化成简单的矩阵运算,计算量较小,而且保守性比基于区间、椭球和平行多面体的方法小,所以近年来受到了很多学者关注,并取得了很多成果[13−17].由于集员滤波是保证状态估计,即实际状态始终在估计的状态可行集范围内,因而基于集员滤波的故障检测与分离方法也具有保证性,即如果出现故障警报,则一定有故障发生[18].文献[19]基于集员估计进行MIMO系统的故障检测.文献[20]提出了一种将未知输入观测器与集员方法相结合进行鲁棒故障诊断的方法.文献[21]基于全对称多胞形设计一组区间观测器,并求得全对称多胞形形式的结构化残差,在此基础上设计了故障诊断策略.

目前大部分基于模型的故障诊断的研究都集中在残差生成方面,而对于故障检测阈值的研究还不是很完善.集员估计方法能够给出区间估计结果,所以能够用来生成故障检测的动态阈值.实际系统中广泛存在的参数不确定性增大了故障诊断的难度,容易引起误报,而集员估计可以方便地处理参数不确定性,并且可以消除误报.目前大部分利用集员估计方法进行故障诊断的研究结果都集中于故障检测方面[22−25],故障分离方面的研究非常少见,但是故障分离对于主动容错控制非常重要.本文针对存在参数不确定性的线性系统,基于全对称多胞形集员估计设计未知输入故障诊断滤波器,将特定故障视为未知输入,使滤波器对其解耦,但对其他故障敏感.设计的滤波器可以估计出无故障情况下测量输出的动态边界,作为故障检测的动态阈值,最后基于一组滤波器设计故障分离策略.本文提出的方法结合了未知输入解耦和集员估计的优点,能够在存在参数不确定性,干扰和噪声概率分布未知的情况下实现故障检测和分离,并且保证零误报率.最后通过VTOL飞行器的线性化纵向模型仿真验证了本文所提方法的有效性.

1 问题描述及相关概念

考虑如下带有参数不确定性的线性离散系统

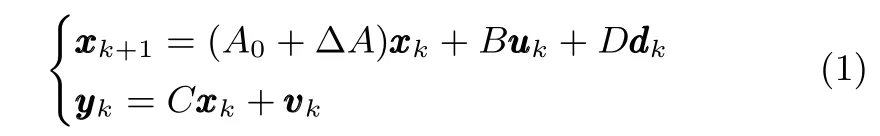
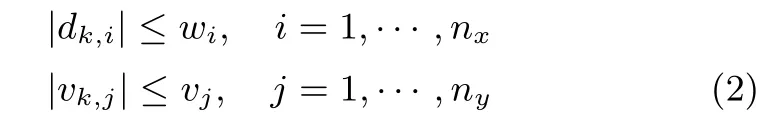
其中,dk,i,vk,j分别为k时刻过程干扰的第i个分量和测量噪声的第j个分量,wi,vj分别为过程干扰和测量噪声的最大幅值,令分别表示以wi,vj为对角元素的对角矩阵,即

分别称为干扰强度矩阵和噪声强度矩阵.参数不确定性矩阵ΔA也满足未知但有界假设,即

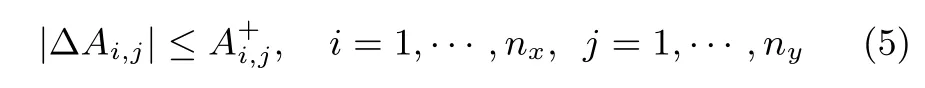
其中,ΔAi,j为ΔA的第i行第j列的元素,为已知常数矩阵第i行第j列的元素.

本文用全对称多胞形界定系统变量和不确定性参数的取值范围,全对称多胞形的定义如下:

定义1.s阶全对称多胞形是超立方体Bs=[−1,+1]s的仿射变换,即

其中,⊕为闵科夫斯基和,常向量称为Z的中心,H称为Z的生成矩阵.

执行器发生加性故障时,状态空间模型可以表示为

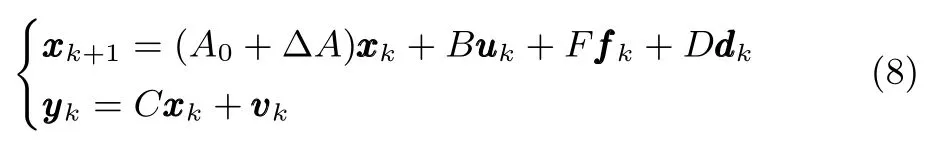
其中,m为可能的故障模式数目.

考虑单一执行器故障的情况,当第i个执行器发生加性故障时,因为故障是通过输入矩阵B的第i列对系统造成影响的,此时故障作用矩阵F=Bi,Bi为输入矩阵B的第i列.

为了保证故障是可分离的,本文假设

本文的目标是针对系统(8)设计一种未知输入集员滤波器,把故障视为未知输入,在存在参数不确定性情况下做到保证状态估计,即保证实际状态始终保持在估计状态范围内.然后针对每种执行器故障设计一个滤波器,用一组滤波器同时进行状态估计,并在此基础上进一步设计故障检测和分离策略.

2 未知输入集员滤波器设计

本节的目标是设计一种基于全对称多胞形的未知输入集员滤波器.集员滤波器估计的是状态可能的范围,类似于卡尔曼滤波器,集员滤波器也由状态预测和测量更新(校正)两个基本环节组成.

1)状态预测.假设k时刻的状态向量满足,在内的状态沿状态方程传播到k+1时刻,状态可能的取值范围为,一般无法求解的准确范围,但可以求得近似集合,满足称为状态预测集.

2)测量更新.给定k+1时刻的测量输出,与测量输出保持一致的状态集合为,测量更新的目标是计算状态预测集合和的交集,一般情况下也较难求解的解析解,但可以求解近似集合作为测量校正后的状态估计范围,满足.

定理1.对于存在参数不确定性的离散系统(8),假设k时刻的状态满足,其中,,则存在全对称多胞形,使得k+1时刻的状态满足,其中,,,由下式求得

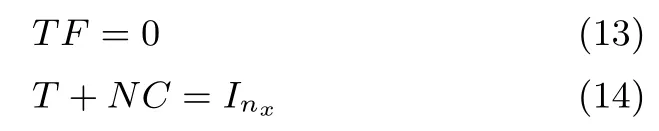
其中,M1(i,i)为M1第i个对角元素,pk,j表示的第j个分量;M2(i,i)为M2第i个对角元素,φ=A+|Hk|,φi,j为φ的第i行第j列的元素.

证明.首先需要使状态方程对指定故障解耦,将式(8)的状态方程两边分别左乘矩阵T,根据式(13)得

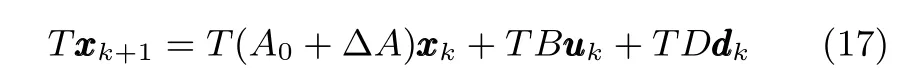
再根据式(14)可得

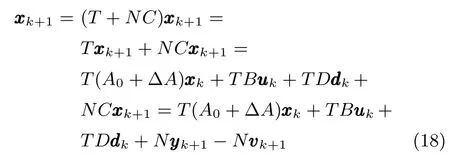
由式(18)和其中各变量的取值范围可得

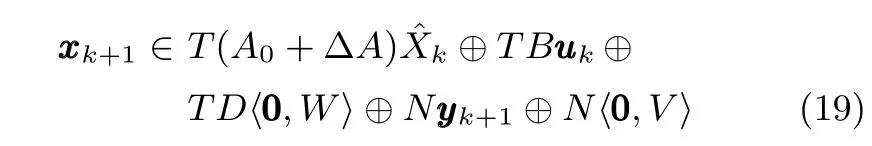
为了接下来的证明,引入全对称多胞形Z=〈p,H〉的如下性质[16]

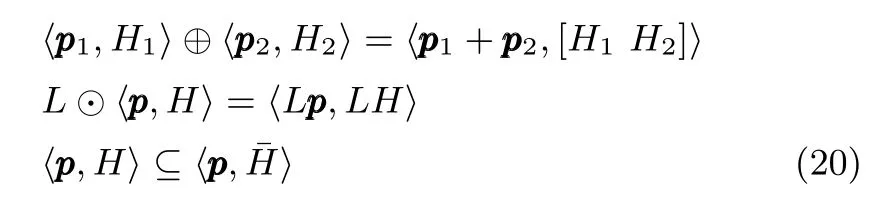
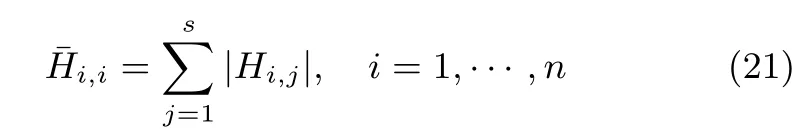
在系统矩阵是确定矩阵的情况下,根据全对称多胞形的性质(20)很容易计算出xk+1的范围,但是因为系统矩阵(A0+ΔA)存在参数不确定性,引入了不确定性集合的乘积,即.为了计算,下面引入实数区间的基本运算法则.对于任意实数区间[a,b]和[c,d],根据文献[26],实数区间四项基本运算法则如下:

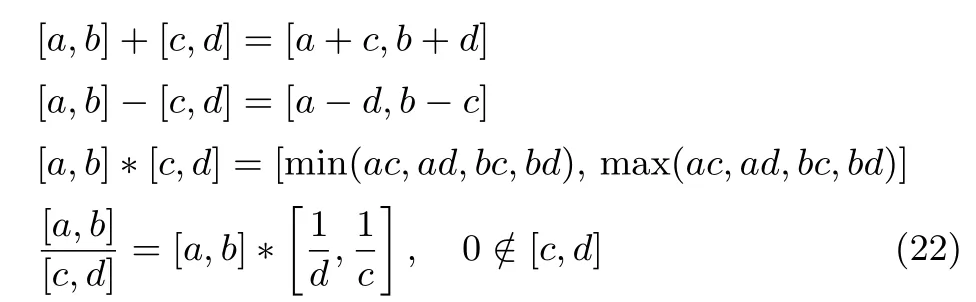
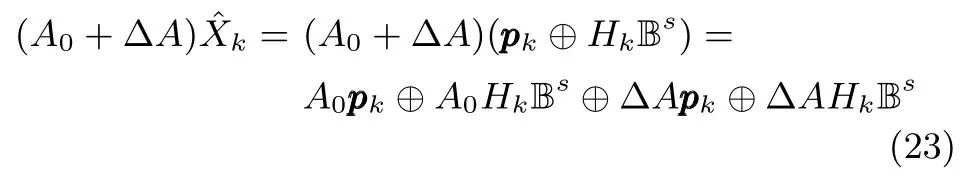
由区间基本运算法则(22)和矩阵的乘法容易得到

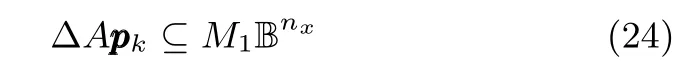
同理可得

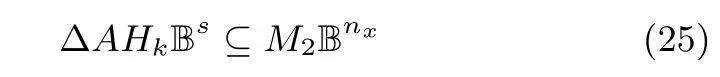
再由全对称多胞形的基本性质(20)可以得到

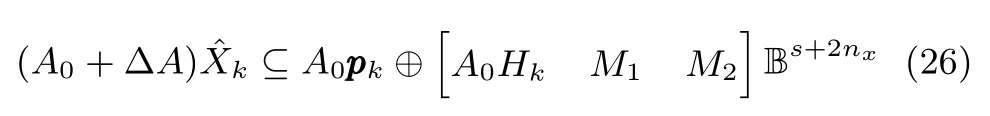
将式(26)代入式(19),并继续利用全对称多胞形的基本性质(20)可得状态的预测范围

矩阵T和N的可行解为[27]

其中,(CF)+为矩阵CF的伪逆,可以用下式求解

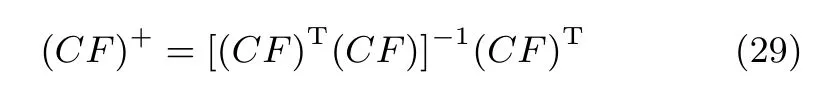
定理 2.给定矩阵,全对称多胞形和多面体,其中,.定义向量和矩阵,其中,为对角矩阵.则存在一个以Λ为参数的全对称多胞形族Zˆ(Λ)能够包含Z和P的交集,满足

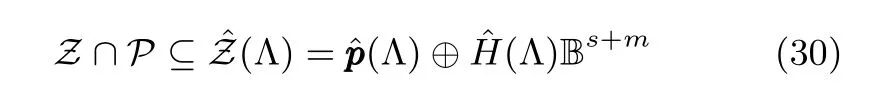
对于系统(8),根据定理2,如果k+1时刻的状态预测集为,则存在全对称多胞形族,满足,其中,,并由下列各式求得

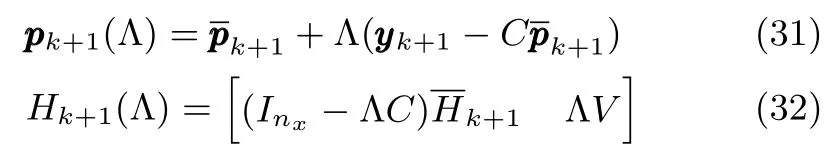
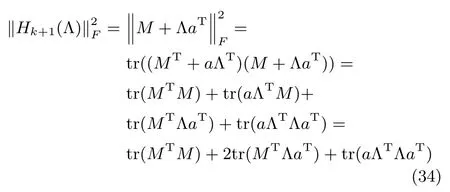
其中,tr(·)表示矩阵的迹,且对任意维数相容的矩阵X,Y,满足tr(XY)=tr(YTXT).所以可以求出使得‖Hk+1(Λ)‖F最小化的Λ值为

定理3.给定全对称多胞形和整数,将矩阵G的每一列按照欧氏范数的大小降序排列得到新的矩阵,则有其中,由的前s−n列组成,是一个对角矩阵,其对角元素为

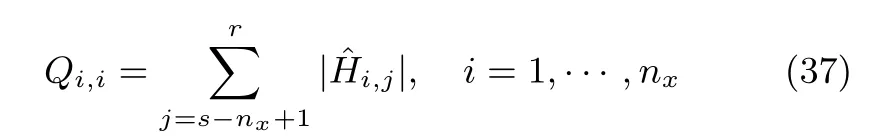
3 故障诊断策略

上一节设计了对于特定故障解耦的未知输入集员滤波器.本节考虑单一执行器故障,此时故障模式总数m=nu,针对每个执行器设计一个滤波器,基于一组这样的滤波器设计故障诊断策略.故障诊断策略的原理图如图1所示.

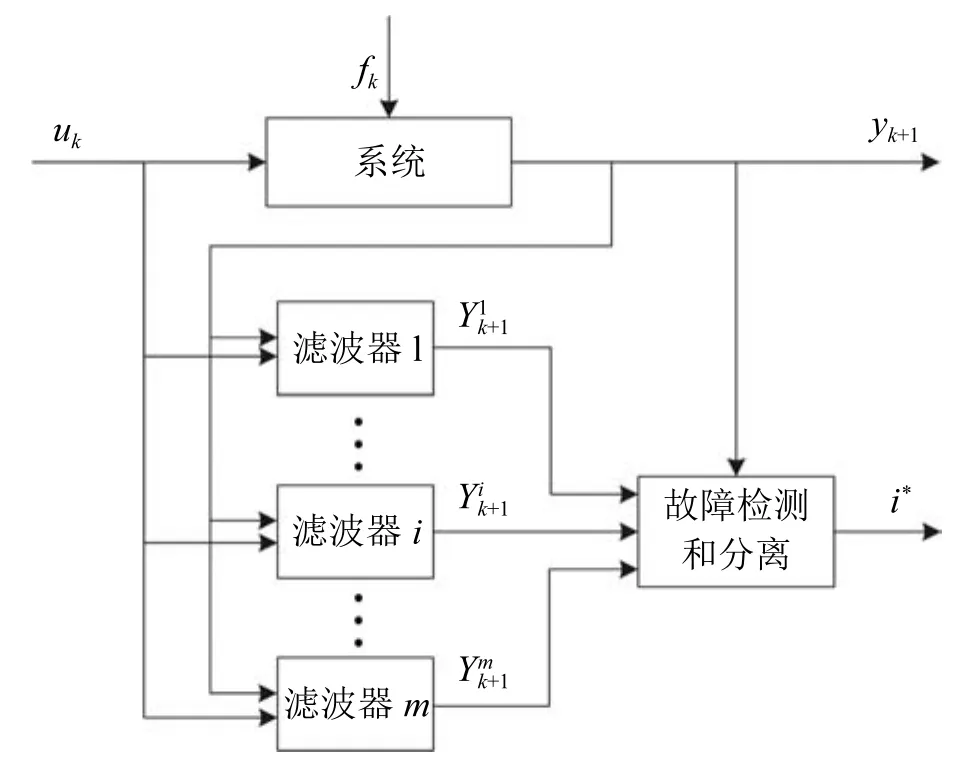
图1 考虑单一故障时的故障诊断原理示意图Fig.1 Fault diagnosis scheme for single fault scenario

第i个滤波器对第i个执行器的故障解耦,在没有执行器发生故障或第i个执行器发生故障时,滤波器i都能做到保证状态估计.基于已经对故障解耦的状态方程(18)求解的状态预测集 也是实际状态的保证状态估计,与保持一致的测量输出的集合为

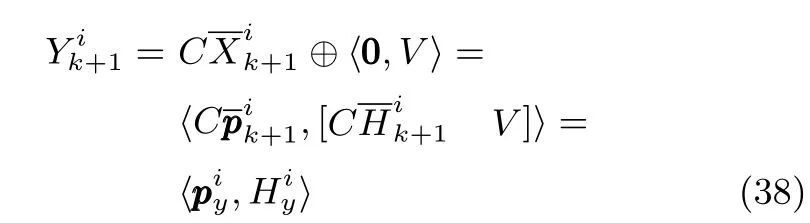
其他滤波器由于没有对第i个执行器的故障解耦,当第i个执行器发生故障时,即F=Bi时

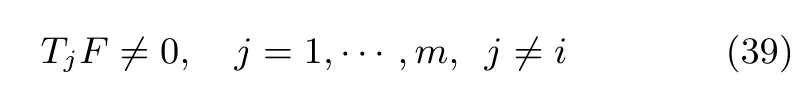
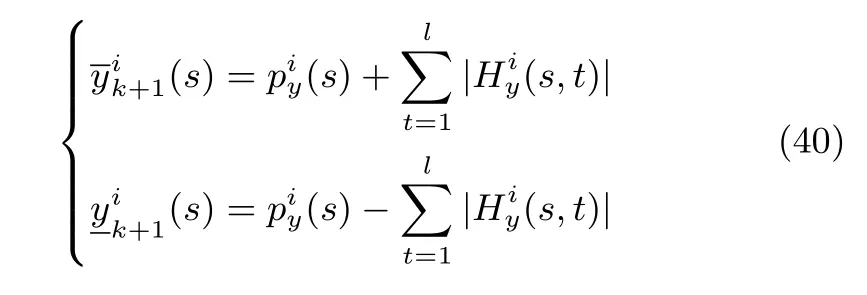
则可以判断故障发生.

所以故障检测和分离策略如下:

1)故障检测.在k+1时刻如果存在s,s=1,···,ny和i,i=1,···,m使得滤波器i满足式(41),则可以判断,说明发生了故障.

2)故障分离.当检测到故障时,如果存在第i∗个滤波器对于所有测量输出分量均不满足式(41),则说明第i∗个执行器发生了故障.

注1.当发生并发故障时,针对单一故障设计的滤波器都会检测出故障,所以无法进行故障分离.与文献[27]中的方法一样,本文的方法也可以推广到系统中同时有两个执行器发生故障的情况.如果每种故障模式的故障作用矩阵都满足假设式(10),则可以针对每种故障模式设计一个未知输入集员滤波器,因为总共有种故障模式,所以需要设计个滤波器.当系统处于第i种故障模式时,只有i个滤波器对第i种故障模式完全解耦,而其他滤波器都会受到故障影响.所以满足所有测量输出分量始终保持在上下边界之间的滤波器的编号即为发生的故障模式编号,从而实现了故障检测和分离.

4 仿真分析

为了验证本文所提方法的有效性,本节利用VTOL飞行器线性化纵向模型进行仿真验证[28].其状态空间表达式为

求解未知输入解耦矩阵T和N时,矩阵S取为

情形1.假设执行器1在t=1s时发生加性故障,具体形式可以表示如下:

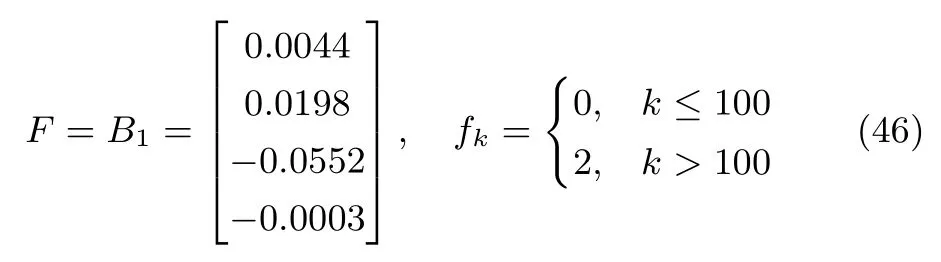
并且过程干扰满足

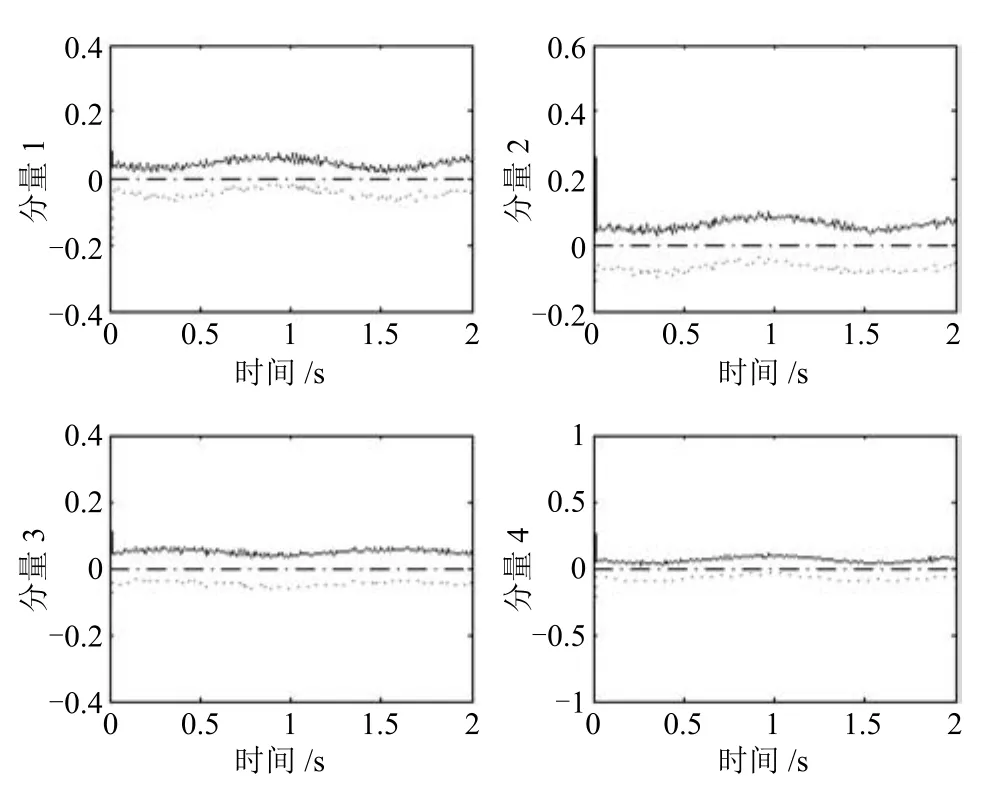
图2 执行器1故障时滤波器1的仿真结果Fig.2 The simulation results of the first filter with the first actuator in fault

情形2.假设执行器2在t=1s时发生加性故障,具体形式可以表示如下:

并且过程干扰同样满足式(47).

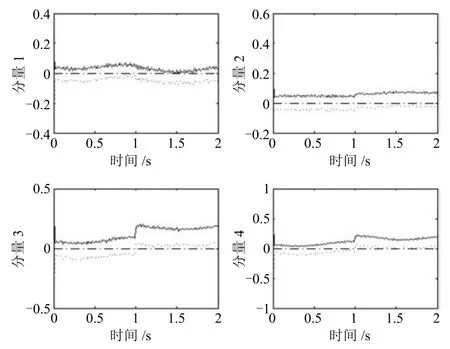
图3 执行器1故障时的滤波器2的仿真结果Fig.3 The simulation results of the second filter with the first actuator in fault

仿真结果如图4和图5所示,各曲线的含义与图2和图3相同.从图4可以看出,滤波器1的第2个和第4个分量都在t=1s附近检测出了故障;从图5可以看出,滤波器2的各个分量都不满足式(41),即测量输出的各个分量都在滤波器2估计的状态边界之间.因此按照设计的故障诊断策略检测出了t=1s附近发生了故障,发生故障的是执行器2.

图4 执行器2故障时滤波器1的仿真结果Fig.4 The simulation results of the first filter with the second actuator in fault

为了充分说明本文所提方法的优势,下面将本文的方法和不使用集员滤波的方法进行对比.具体将本文的方法与文献[27]中的方法进行对比.文献[27]的故障诊断策略与本文的相似,同样基于未知输入解耦设计一组滤波器,但使用的是非集员方法.为了使用文献[27]中的方法,需要假设过程干扰和测量噪声是高斯分布的,但本文研究的系统中过程干扰和测量噪声的概率分布是未知的,所以只能假设其边界值为3σ,σ为过程干扰和测量噪声分量的标准差,并由此近似计算出它们的方差矩阵.仿真参数设置与情形2相同,使用文献[27]中的方法得到的仿真结果如图6所示.

图5 执行器2故障时滤波器2的仿真结果Fig.5 The simulation results of the second filter with the second actuator in fault

图6 文献[27]中方法的仿真结果Fig.6 The simulation results of the method in[27]

如果过程干扰或测量噪声的动态特性在不同时间段内相差较大,则在一个时间段内人为设定的阈值在另一个时间段就很有可能不适用了.图7为无故障时文献[27]中方法的仿真结果,过程干扰设为

从图7可以看出,t=2s前后的残差模大小区别很大,所以很难人为设定阈值.另外这种方法不能有效地处理参数不确定性,在无故障时,如果状态变量较大,很容易出现误报.

相比文献[27]中的方法,本文提出的方法的优势在于可以自动生成故障检测阈值,避免了人为选取阈值的麻烦,并且可以很好地处理参数不确定性,同时保证零误报率.

图7 无故障时文献[27]中方法的仿真结果Fig.7 The simulation results of the method in[27]without fault

5 结论

本文针对存在参数不确定性的线性系统,设计了一种基于未知输入集员滤波器的故障诊断方法.首先使系统状态对特定故障解耦,基于全对称多胞形表示系统状态的不确定性范围,并利用全对称多胞形的性质和区间运算规则处理参数不确定性,设计出了一种未知输入集员滤波器.然后通过所设计的滤波器估计测量输出的上下边界,并基于一组滤波器进行故障检测和分离.最后通过对VTOL飞行器的仿真分析验证了本文所提方法的有效性.本文提出的故障诊断方法基于集员滤波器,由于集员滤波器的状态估计存在保守性,导致故障检测存在一定的保守性.因此如何进一步减小状态估计的保守性,降低故障漏检率有待继续研究.