PARALLEL COMPUTING METHOD OF PURE ALTERNATIVE SEGMENT EXPLICIT-IMPLICIT DIFFERENCE SCHEME FOR NONLINEAR LELAND EQUATION∗†
2018-10-13RuifangYanXiaozhongYangShuzhenSun
Ruifang Yan,Xiaozhong Yang,Shuzhen Sun
(Institute of Information and Computation,Mathematics and Physics School,North China Electric Power University,Beijing 102206,PR China)
Abstract The research on the numerical solution of the nonlinear Leland equation has important theoretical significance and practical value.To solve nonlinear Leland equation,this paper offers a class of difference schemes with parallel nature which are pure alternative segment explicit-implicit(PASE-I)and implicit-explicit(PASI-E)schemes.It also gives the existence and uniqueness,the stability and the error estimate of numerical solutions for the parallel difference schemes.Theoretical analysis demonstrates that PASE-I and PASI-E schemes have obvious parallelism,unconditionally stability and second-order convergence in both space and time.The numerical experiments verify that the calculation accuracy of PASE-I and PASI-E schemes are better than that of the existing alternating segment Crank-Nicolson scheme,alternating segment explicit-implicit and implicit-explicit schemes.The speedup of PASE-I scheme is 9.89,compared to classical Crank-Nicolson scheme.Thus the schemes given by this paper are high efficient and practical for solving the nonlinear Leland equation.
Keywords nonlinear Leland equation;pure alternative segment explicitimplicit scheme(PASE-I);stability;truncation error analysis;parallel computing;numerical experiments
1 Introduction
In financial engineering and the modern finance,the most creative work is undoubtedly partial differential equations of option price which was derived by Black-Scholes and Merton in 1973.The result is a milestone in the history of financial derivative securities and sets a foundation for the reasonable pricing of various derivatives of the emerging derivative markets.The innovation of the model is that the option price does not depend on the personal preference of investors,but on the Black-Scholes model under too many assumptions which are inconsistent with the actual situation,such as no taxes and transaction fee,no arbitrage opportunities,et al.[1-4].Therefore,the nonlinear Black-Scholes model has been the focus of academic research in the last 20 years.
Taking into account of the effect of payment transaction costs,Leland[5]improved the Black-Scholes model.Then Hoggard,Whalley and Wilmott[6]obtained option pricing formula under the transaction costs.Since it is almost impossible to find the exact analytic solution of the nonlinear Black-Scholes model[7],the numerical solution of the nonlinear Black-Scholes equation is of practical financial significance.Company et al.[8,9]gave a semi-discrete solution of the nonlinear Black-Scholes equation,and proved the consistency and stability of the numerical scheme.Pascal[10]gave an implicit numerical scheme for solving nonlinear option pricing models.When numerically solving multidimensional Black-Scholes equation or calculating the number of grid points,the required computation time will be exponentially increased and the computational efficiency will be declined.Thus the main problem here is that it is difficult to meet the requirements of the timeliness in the option pricing.
Along with the rapid development of high performance computer as well as the application of multi-core and cluster technology,parallel numerical method has turned into a new branch of science.It enriches the content of the traditional calculation methods and becomes an important research direction of computational mathematics.For parallel numerical methods,Evans and Abdullan[11]proposed grouping explicit ideas.For the implicit scheme,it has good stability but is not suitable to be solved in parallel.Inspired by grouping explicit methods,Zhang et al.[12,13]proposed the idea of constructing segment implicit using Saul’yev asymmetric scheme,and properly used the alternating technology to establish a variety of explicit-implicit and pure alternating implicit parallel method.The effect of stability and parallelism was obtained,but the accuracy was not very high due to the use of asymmetric scheme in the inner boundary points.Han et al.[14]constructed a class of pure alternating explicit implicit difference numerical methods,and proved the unconditional stability and high accuracy of the scheme for the diffusion equation.Zhang et al.[12,13] first named the most general explicit implicit hybrid scheme of the parabolic equation as difference scheme with parallel nature,then analyzed the theoretical issues such as the existence,uniqueness,convergence and stability of difference scheme solution,and established the basic theory of difference method with intrinsic parallelism.Now,these parallel difference schemes have been applied to the discrete solution of many development equations.For example,Wang[15]constructed a finite difference scheme with parallel nature for the Korteweg-de Vries(KDV)equation,and the linear absolute stability of the scheme was proved.Yuan et al.[16]proposed a parallel difference scheme with second-order accuracy and unconditional stability for nonlinear parabolic equation.
There are two kinds of parallel difference methods,one of which is developed from the point of view of numerical algebra parallel computing.For example,Hao et al.[17]suggested a parallel iterative method for solving the fully implicit difference scheme on parabolic equations.The other kind is based on the exploration of the parallel of the traditional difference scheme.Such as,Wu et al.[18]presented a difference method with intrinsic parallelism which is alternating segment Crank-Nicolson(ASC-N)difference scheme.And Zhao et al.[19]proposed the alternating segment explicit-implicit(ASE-I)and implicit-explicit(ASI-E)difference schemes for nonlinear Leland equations.But the calculation accuracy is poor due to the asymmetric form of its inner boundary.In order to improve the whole accuracy of the calculation,we can apply classical explicit and classical implicit to connect the inner boundary points.Then we get pure alternative segment explicitimplicit(PASE-I)and pure alternative segment implicit-explicit(PASI-E)difference schemes.Theoretical analysis and numerical experiment demonstrate that these schemes are absolutely stable and second-order accurate.Numerical experiment also shows that these two schemes are better than the existing ASC-N scheme,ASE-I scheme and ASI-E scheme,and the computational efficiency is much higher than the classical C-N scheme.
2 The PASE-I Scheme
2.1 The nonlinear Leland equation
In order to solve the nonlinear Leland equation,the initial and boundary value condition of nonlinear Leland equation will be given in this section.Considering that the underlying asset is the transaction cost-paying stock,by the slack-hedging principle,we can get the following nonlinear Leland equation[1-4]:

Here V is the price of European call option(dollar),S is the price of the underlying asset,r is risk-free interest rate,is the revised volatility,In the revised volatility,is the Leland number,σ is the volatility,k is a volume of transaction cost,δt is the time difference between the two transactions and t is the time.

In order to numerically solve the equation of the European call option pricing with transaction costs,we combine equation(1)with the corresponding boundary conditions as follows[1-4]:
(i)V(S,t)=max{S−K,0},that is,the price is its pay-o ffwhen the option expires and K is the strike price.
(iii)V(0,t)=0,that is,once the stock price is zero,it will not return to the original state generally.
In theory,the solving area of equation(1)is

But in the actual transaction,the price of the underlying asset will not always appear to be zero or infinity.Therefore,the financial institution provides a small enough value Smin>0 as the lower bound and a large enough value Smax>0 as the upper bound for it.Then the pricing problem can be solved in the bounded area
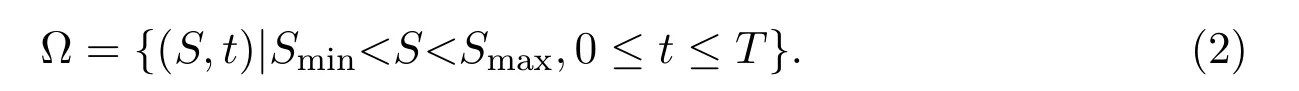
We need to solve equation(1)for the European call option with the initial condition

and the boundary conditions

In order to solve problem(1)-(4),we can substitute its variables as follows[1-3]:
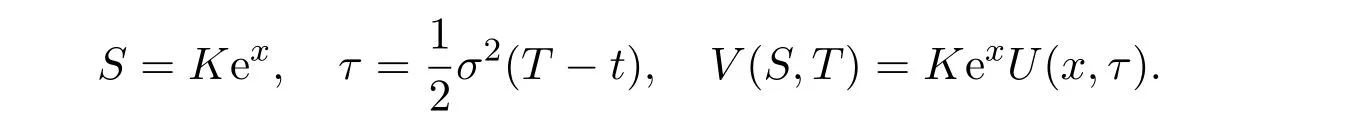
Then this pricing model(1)will be transformed into the initial-boundary value problem of a partial differential equation with constant coefficients:

Then the initial condition will be translated into

And the boundary conditions will be translated into

The solution region is transformed intoWhen making specific calculation,we can select the number M+of sufficiently large and M−of small enough.The value region is changed to[M−,M+],and the boundary condition is transformed into

2.2 Construction of the PASE-I scheme
Let us make a mesh partition on the area Ω and consider the function U(x,τ)at the discrete set of points
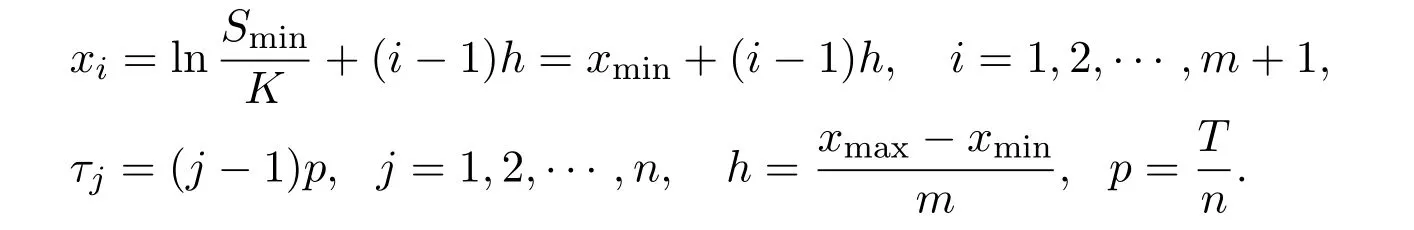
Here h is the space step,p is the time step,and m,n are the numbers of grid points in the x and t directions,respectively.We useto denote the solution of equation(5)at point U(xi,τj).In order to construct the PASE-I scheme,we give some difference schemes of the equation(5).Let
First,the classical explicit scheme is
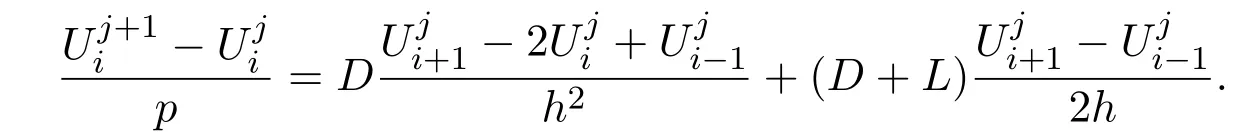
The above scheme can be written as

Second,the classical implicit scheme is

which can be transformed as

Since the classical explicit scheme(6)has the ideal parallelism,it is very suitable for the parallel computing.But this scheme is only conditionally stable.Classical implicit scheme(7)is absolutely stable,so it is not easy to apply the scheme in parallel machine directly and effectively due to the difficulty of solving three diagonal equations[20].In order to combine the classical explicit scheme(6)and the classical implicit scheme(7),we construct a special class of hopscotch algorithm for solving problem(1)-(4).We separate the space net points into finite segments,and use pure explicit scheme(6)and pure implicit scheme(7)alternating on the segments.Then we use alternating technique again in the time direction.The specific scheme is as follows.
Let m−1=(2s+1)l=Nl,here N is an odd number and s,l∈Z+,l≥3(Z+represents positive integer).We divide points on each time layer into the(2s+1)sections and mark in sequence as S1,S2,···,S2s+1.In even time layer,the calculated points are arranged from left to right by the rules of classical explicit scheme-classical implicit scheme-classical explicit scheme.And in odd time layer,the computation scheme is carried out alternately,that is,classical explicit scheme is replaced by classical implicit scheme while classical implicit scheme is replacd by classical explicit scheme.The calculation rule becomes classical implicit schemeclassical explicit scheme-classical implicit scheme.In Figure 1,we use the classical explicit scheme in circle and the classical implicit scheme in square.

Figure 1:Schematic diagram of the PASE-I scheme
Solution for each implicit segment depends on the calculation of the first or last point of the adjacent explicit segment,which gives the inner boundary value.There is a certain correlation between the computation of the explicit segment and the implicit segment in any time layer,that is,calculation of implicit segment is not completely independent.Therefore,we can perform parallel calculation on the explicit segment first,and then on the implicit segment based on the endpoint value given by the explicit segment.
The matrix form of the PASE-I scheme is

where j=1,3,···,n − 1.
Here I is a unit matrix of(m−1)×(m−1)order,G1and G2are matrices of(m−1)×(m−1)order,specifically given by

2.3 Existence and uniqueness of numerical solution of PASE-I scheme
From the initial-boundary value condition of Leland equation,we can get the value of the first layer of difference scheme(8).Assuming that the valueof the(2j−1)-th time layer is known,the matrix equation for calculating the value of the 2j-th time layer is

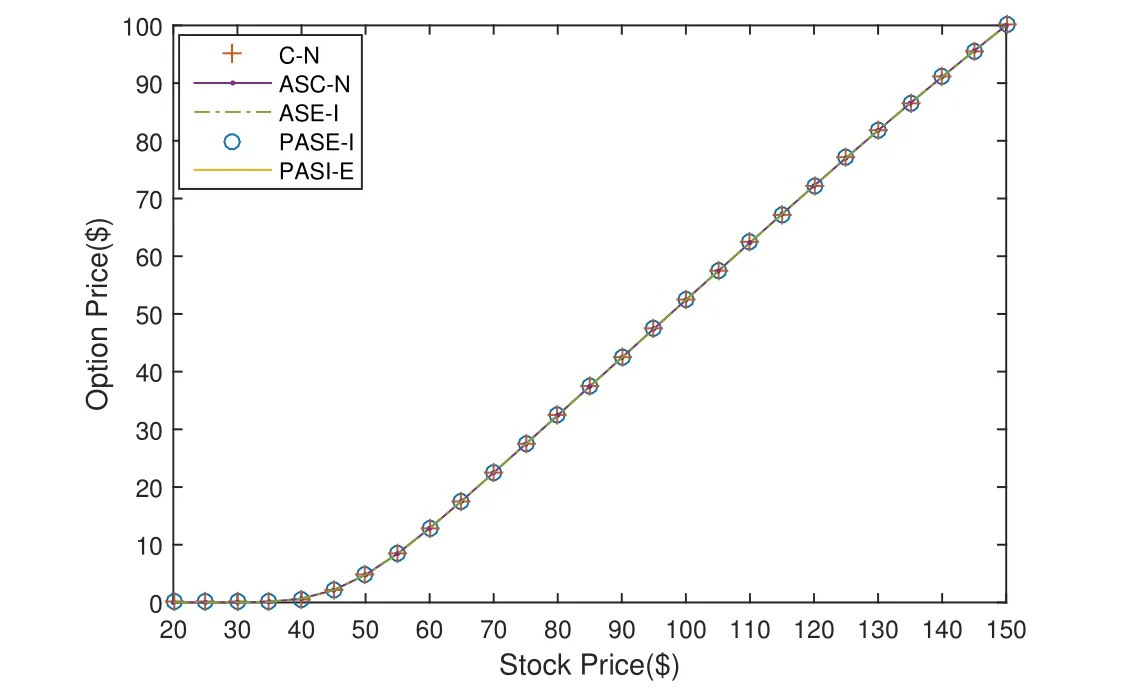
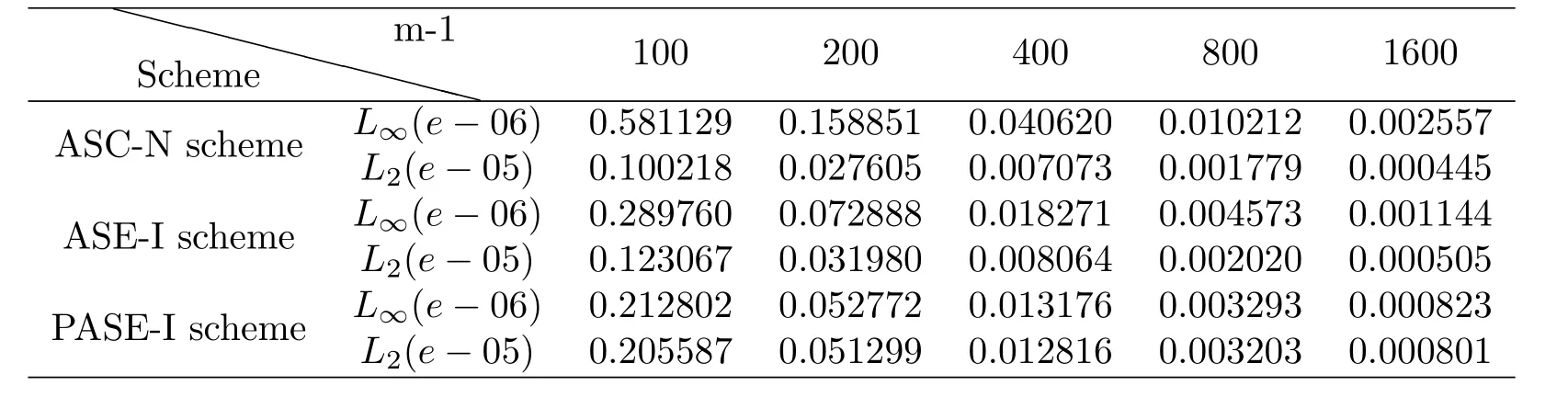
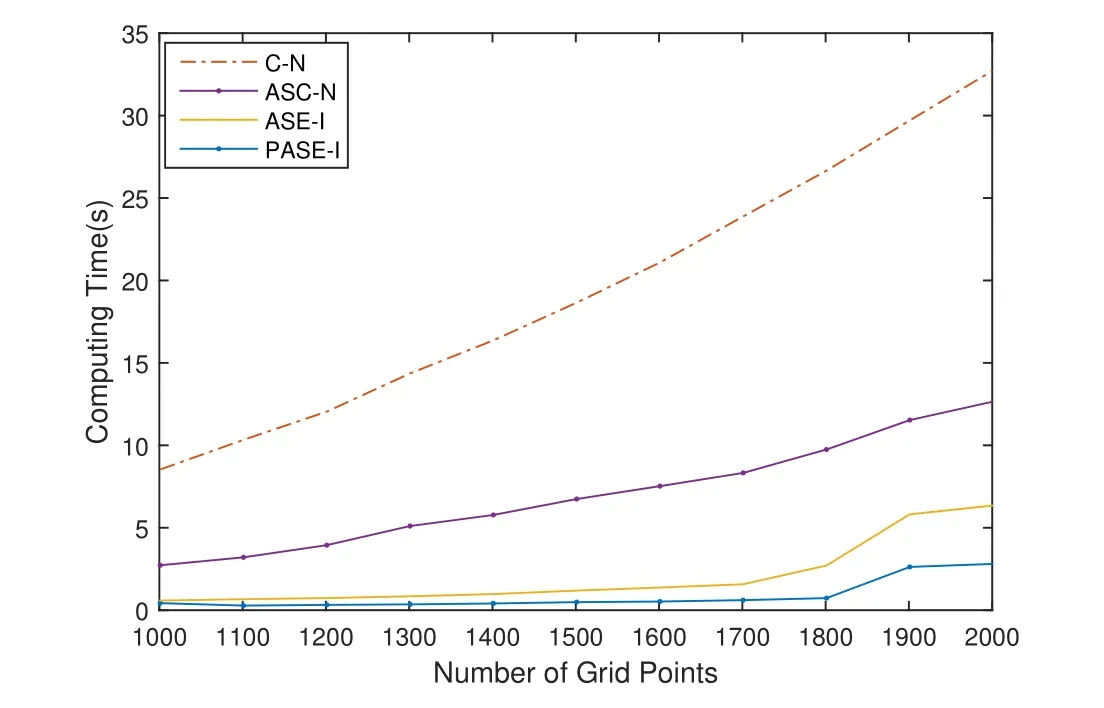
The coefficient matrix is I+r1G1.If I+r1G1is a non-singular matrix,(9)has only one solution.So for the coefficient matrix I+r1G1,we just need to prove that the implicit part is non-singular.From the expression of Gl,we can see that Glis a diagonally dominant matrix when a In the same way,assuming that the valueof the 2j-th layer is known,the matrix equation for calculating the value of the(2j+1)-th layer is We can also prove that equation(10)also has a unique solution. Based on the above analysis,we will get the following theorem. Theorem 1For solving nonlinear Leland equation,the solution of the PASE-I scheme(8)is existing and unique. The stability of the PASE-I scheme(8)for solving the nonlinear Leland equation will be analyzed in this section.The growth matrix of the PASE-I scheme is In order to discuss the stability of PASE-I scheme(8),we need two lemmas as follows. Lemma 1[1]If ρ ≥ 0 and C+CTis a non-negative real matrix,then(I+ρC)−1exists,and Lemma 2and r2G2in the growth matrix of the PASE-I scheme(8)for solving the nonlinear Leland equation are non-negative matrices. We just need to testify thatandare non-negative real matrices,because in the process of obtaining the solution for each implicit segment,its inner boundary value only depends on the calculation of the first or last point of the adjacent explicit segment. From By Lemma 1,we can easily get the following estimation Then we can get Therefore,we get the following theorem. Theorem 2The PASE-I scheme(8)for solving the nonlinear Leland equation is unconditionally stable. The accuracy of classical explicit-implicit(E-I)scheme and classical implicitexplicit(I-E)scheme is[19].In the inner boundary points,the accuracy analysis of the PASE-I format will be given below.Performing Taylor expansion at the pointfor the explicit scheme(11)and implicit scheme(12),and denoting the truncation errors as T1(p,h)and T2(p,h)respectively,we can get Here,α+β=4.Taking into account then we can obtain From the expressions of(13)and(14),we can see parts of the error terms will cancel each other.Therefore,the accuracy in interior boundary points is secondorder convergent.Accordingly,we can get the following theorem. Theorem 3For the nonlinear Leland equation,the accuracy of PASE-I scheme(8)is For the existing ASC-N scheme,ASE-I scheme and ASI-E scheme of the nonlinear Leland equation,the accuracy in ‘interior boundary points’is close to secondorder,because the accuracy of Saulyev asymmetric scheme is O(p2+h2)and the overall accuracy is reduced.Thus,the precision of PASE-I scheme is better than that of the existing ASC-N scheme,ASE-I scheme and ASI-E scheme.The theoretical analysis will be testified in the following numerical experiment. Similarly,we can get the pure alternating segment implicit-explicit(PASI-E)scheme of the nonlinear Leland equation as follows where j=1,3,···,n − 1.With the analysis similar to that of the PASE-I scheme,we can get the following theorem. Theorem 4For the nonlinear Leland equation,the solution of the PASI-E scheme(15)is existing and unique,unconditionally stable and second-order convergent is O(p2+h2). For comparison,we choose the numerical example in[18,19].Numerical experimentation is based on Core i5-2400 CPU Intel,running in the Matlab R2014b environment. Example 1[18,19]We consider a European call option on stocks with transaction cost.Assuming the initial price of the underlying stock is 70 dollars,the strike price of option is 50 dollars and the risk-free interest rate is 0.01 per year.The deadline of the options are 3,6,9 and 12 months.The volatility is 0.2 per year and the ratio of transaction cost is 0.02,δt is(considering the case of paying transaction costs monthly). SolutionDenote the following symbols: Figure 2:Comparison of numerical results for several different schemes From Figure 2,we see the PASE-I scheme solution and the PASI-E scheme solution of the nonlinear Leland equation are well approximated by C-N scheme solution of the option pricing model(2).And there appears little difference from the existing ASC-N scheme solution,ASE-I scheme solution and ASI-E scheme solution. In particular,when the stock price was$70,we give the option price at different time,computing time as well as the relative error at T=6.The calculation results are shown in Table 1. Table 1:Comparison of numerical results and the analytic solution of several schemes From Table 1,we can get the calculating time of PASE-I scheme and PASI-E scheme as 0.2822s and 0.2530s respectively at T=6.The efficiency is higher than the existing C-N scheme and ASC-N scheme.The relative errors of PASE-I scheme solution and PASI-E scheme solution are 1.59633307×10−1and 1.54742036×10−7respectively,so we can expect that the PASE-I scheme solution and PASI-E scheme solution are very close to the C-N scheme solution. We know that the accuracy of PASE-I scheme and that of PASI-E scheme are consistent.Therefore,we only need to compare the convergence precision of PASE-I scheme and ASC-N scheme.We regard the solutionof the classical C-N scheme as the control solution.Also we view the solutionof the PASE-I scheme,ASE-I scheme and the ASC-N scheme as perturbation solutions.The definitions of L2-error and L∞-error are as follows The convergence order of space(COS)and the convergence order of time(COT)are defined as follows[21]. Table 2:Comparison of L2-error and L∞-error in space(T=6)for several schemes Table 3:Comparison of COS(T=6)for several schemes Table 4:Comparison of L2-error and L∞-error in time(T=12)for several schemes Table 5:Comparison of COT(T=12)for several schemes In Tables 2 and 4,we can see from L2-error or L∞-error,the error of PASEI scheme in time layer or space layer shows little difference from ASC-N scheme and ASE-I scheme.From Tables 3 and 5,we know that ASC-N scheme and ASE-I scheme are second-order convergent in space and close to second-order convergent in time.However,PASE-I scheme is second-order convergent in both time and space.The reason is that in the interior boundary point,ASC-N scheme and ASE-I scheme are use asymmetric scheme to reduce the overall accuracy.In summary,the PASE-I scheme has a higher accuracy than the ASC-N scheme and ASE-I scheme. In order to get a better stability of the PASE-I scheme and the PASI-E scheme,we regard the solutionof the classical C-N scheme as the control solution.Also we view the solutionof the PASE-I scheme and the PASI-E scheme as perturbation solutions.Then we analyze the distribution of the sum of relative error at every time level(SRET)and the difference total energy(DTE)at space grid points.The definitions of DTE and SRET are as follows: The results of numerical experimentation are shown in Figures 3 and 4. Figure 3:The curves of SRET at time layer Figure 4:Distribution of DTE at space grid points Figure 3 gives the sum of relative error at every time level of PASE-I scheme and PASI-E scheme with C-N scheme.We can see that the maximum of SRET is no more than 5 and at the beginning the SRET is larger.With the time elapsing,the SRET decreases rapidly and eventually becomes stable.Figure 4 is the difference total energy of PASE-I scheme and PASI-E scheme with C-N scheme.The overall DTE is between 0 and 2.5×10−6,but it is the biggest number when is equal to 500.This is because when the stock price K is equal to the stock price S,the error will reach the maximum.When K is equal to 50,it is just in the vicinity of m=500.So there is the largest error in the vicinity of m=500.But the overall DTE goes to zero.Notice that the PASE-I scheme and PASI-E scheme of the nonlinear Leland equation are quite approaching to the C-N scheme.It shows that the PASE-I scheme and PASI-E scheme are computationally stable for solving nonlinear Leland equations. As to the computational efficiency,the calculation times of PASE-I scheme,PASI-E scheme,ASC-N scheme and ASE-I scheme are much less than that of C-N scheme in Table 1.This is because the C-N scheme is the serial scheme which needs to solve three diagonal equations by chasing method.But in the calculation of the PASE-I scheme,PASI-E scheme,the ASC-N scheme and ASE-I scheme,the numerical problem Ax=b is divided into five small problems Aix=bi,i=1,2,···,5.And the parallel computation is carried out by using parfor cycle.That is,when parfor is performing,the cycle is divided into separate parts and various parts are then calculated in parallel.Thus,the execution efficiency of the program is improved and calculation time is effectively reduced[22,23]. From the above analysis,it is obvious that parallel difference scheme has the advantage of saving the calculation time.In order to better reflect the superiority of parallel difference schemes,we select different spatial layers.Because of the same computation time of PASE-I scheme and PASI-E scheme,we just need to compare the Sp(speedup,Sp)of the PASE-I scheme,the ASC-N scheme,ASE-I scheme and the C-N scheme.We take the option validity period T=6 and the time layer n=1000,and the space layer m=2001.Results are shown in Table 6 and Figure 5 as follows. Table 6:Comparison of calculating time for several schemes Figure 5:Comparison of computing time for several schemes For the nonlinear Leland equation,we can get from Figure 5 that with the increase of the number of grid,the computation time of the difference scheme is increasing.And the computation time of the C-N scheme is greater than those of the PASE-I scheme,the ASC-N scheme and the ASE-I scheme.This is because that last three schemes use the parallel reduced computation time greatly.However,the computation time of ASC-N scheme and ASE-I scheme are more than PASE-I scheme,which is less efficient than that of PASE-I scheme. From Table 6,compared with the classic C-N scheme,the Spof ASC-N scheme,ASE-I scheme and PASE-I scheme are 2.60,4.94,9.89 in separately.This fully illustrates the highest computational efficiency of PASE-I scheme. For nonlinear Leland equation,the non-symmetric scheme with low accuracy in the inner boundary points is adopted in the ASC-N scheme,ASE-I scheme and ASI-E scheme,and the overall accuracy is close to second-order.The PASE-I and PASI-E difference schemes in this paper are unconditionally stable,and the computational accuracies are second-order in both space and time.So the accuracies of the PASE-I scheme and the PASI-E scheme are better than those of the ASC-N scheme,ASE-I scheme and ASI-E scheme. The computing times of the PASE-I scheme and the PASI-E scheme are far less than C-N scheme because of the properties of parallel computing.The numerical experimentation confirms the validity of the parallel difference method in PASE-I scheme and PASI-E scheme for solving the nonlinear Leland equation.The PASE-I scheme and the PASI-E scheme given by this paper can be extended to solve nonlinear multidimensional B-S equation.When solving the effective pricing problem of multi-asset options,the advantages of the parallel computing will be more apparent. AcknowledgmentsThe authors are indebted to Dr.Lifei Wu of North China Electric Power University for his advice and help.
2.4 Stability of the PASE-I scheme

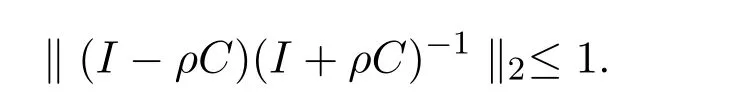
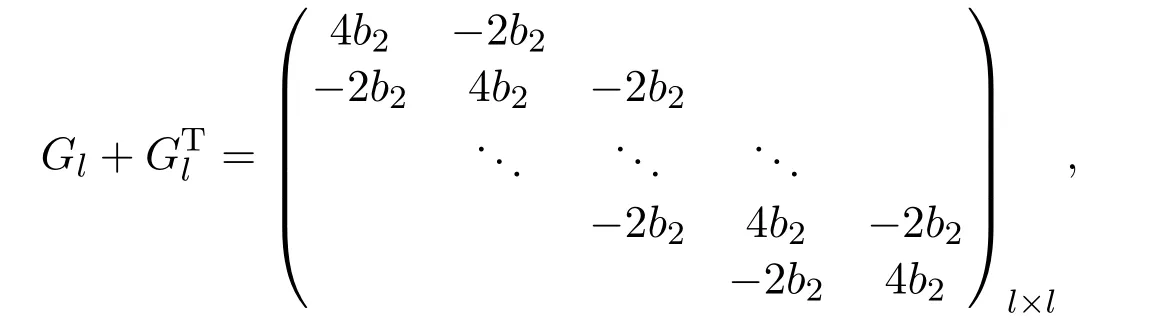

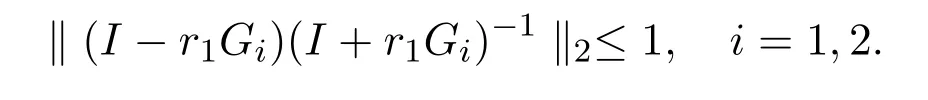
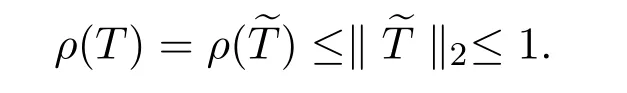
2.5 Convergence of the PASE-I scheme



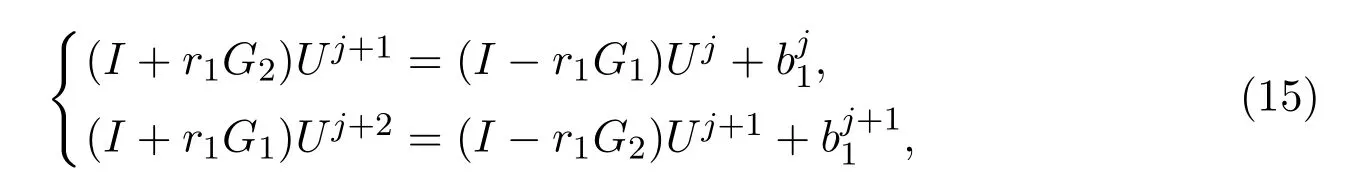
3 Numerical Experiments
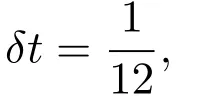











4 Conclusion
杂志排行
Annals of Applied Mathematics的其它文章
- SEMICLASSICAL LIMIT TO THE GENERALIZED NONLINEAR SCHRÖDINGER EQUATION∗†
- THREE KIRCHHOFFIAN INDICES OF THE CACTUS GRAPHS∗†
- ON q-WIENER INDEX OF UNICYCLIC GRAPHS∗†
- SOME LIMIT PROPERTIES AND THE GENERALIZED AEP THEOREM FOR NONHOMOGENEOUS MARKOV CHAINS∗†
- EXISTENCE OF PERIODIC SOLUTION FOR A KIND OF THIRD-ORDER GENERALIZED NEUTRAL FUNCTIONAL DIFFERENTIAL EQUATION WITH VARIABLE PARAMETER∗
- ON THE CONDITIONAL EDGE CONNECTIVITY OF ENHANCED HYPERCUBE NETWORKS∗†
