ON q-WIENER INDEX OF UNICYCLIC GRAPHS∗†
2018-10-13XingFengJianpingOuShaihuaLiu
Xing Feng,Jianping Ou,Shaihua Liu
(1.Faculty of Science,Jiangxi University of Science and Technology,Ganzhou 341000,Jiangxi,PR China;
2.Department of Math.,Wuyi University,Jiangmen 529020,Guangdong,PR China)
Abstract The q-Wiener index of unicyclic graphs are determined in this work.As an example of its applications,an explicit expression of q-Wiener index of caterpillar cycles is presented.
Keywords q-Wiener index;unicyclic graphs;caterpillar cycles
1 Introduction
All graphs considered in this paper are connected and simple.As usual,the distance between two vertices u,v of a graph G is denoted by dG(u,v),or d(u,v)for short.The maximum of such numbers,denoted by d(G),is called the diameter of graph G.
Let u0u1u2···unbe a molecular chain.Note the interaction between two atoms decreases when the distance between them increases.Let q<1 be a positive real number,and suppose that the contribution of atom u1to atom u0is unity.Then the total interaction of atoms to atom u0can be modeled by

And the total interaction between individual atoms of a molecule with graph G can be modeled by the following formula[1,2]
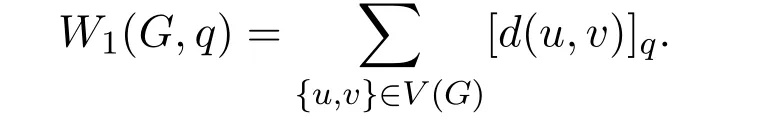
In[1,2],other two concepts of q-Wiener index of a graph G are also introduced as follows
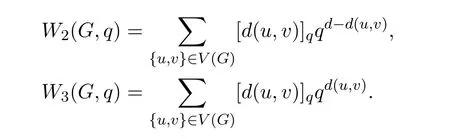
On the one hand,these three q-Wiener indices have close relationship with the classic Wiener index,which can be exemplified by the following equations
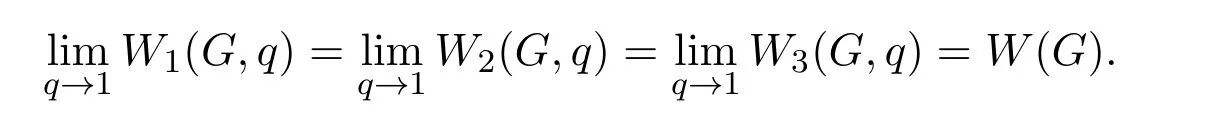
On the other hand,these three q-Wiener indices are also mutually related as follows

The earliest q-analog studied in detail is the basic hypergeometric series,which was introduced in the 19th century[3].q-Analogs find their applications in lots of areas,such as fractals and multi-fractal measures,the entropy of chaotic dynamical systems,and quantum groups.For derails in this field,the readers are suggested to refer to[4,5]for example.Based on equations(1)and(2),in this work,we only consider the first case of q-Wiener index.As a result,the q-Wiener index of unicyclic graphs are determined.As an example of its applications,an explicit expression of q-Wiener index of caterpillar cycles is also presented.
Before proceeding,let us introduce some more symbols and terminology.For any complete graph Knand a forest F,letdenote the graph obtained by pasting one vertex of Knand a vertex of T.For any two trees T1and T2with u∈V(T1)and v∈V(T2),let T1uvT2denote a graph obtained by joining T1and T2with an new edge uv.In this paper,we shall obtain a q-Wiener index ofat first,and then use the obtained observation to determine the q-winer index of unicyclic graphs.For other symbols and terminology not specified herein,we follow that of[6].
2 q-Wiener Index of Unicyclic Graphs
For any two vertices of u and v of G,we writeandthen

When q=1,we have
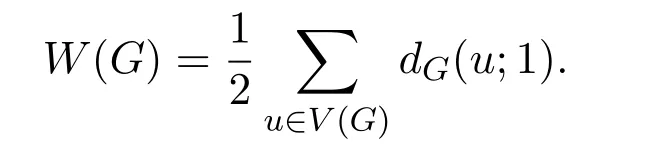
For simplicity,we write W1(G)for W1(G,q)in this paper.
Lemma 2.1[1]Let T1and T2be two trees on n1and n2vertices,respectively,with v1∈V(T1)and v2∈V(T2).If the tree T is obtained by linking v1and v2with an edge,then

Lemma 2.2If we denote by{v1,v2,···,vn}the vertex set of the subgraph Knofby Tithe component ofthat contains vertex viandthen
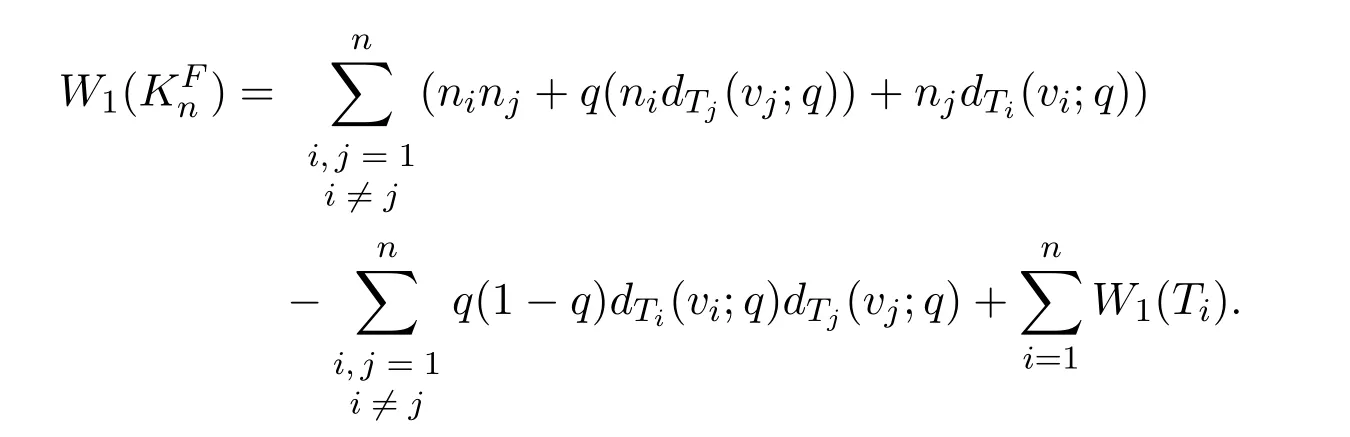
ProofLetBy(1)of Lemma 2.1,we have
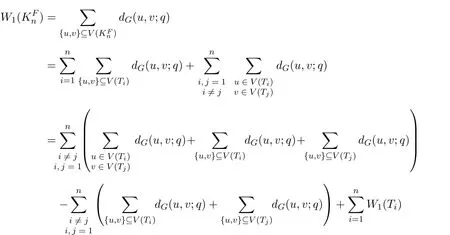

And so,the lemma follows.
Theorem 2.1Let G be a unicyclic graph with cycle C=v1v2···vnv1.If Tiis the subgraph of G−E(C)that contains vertex viandthen
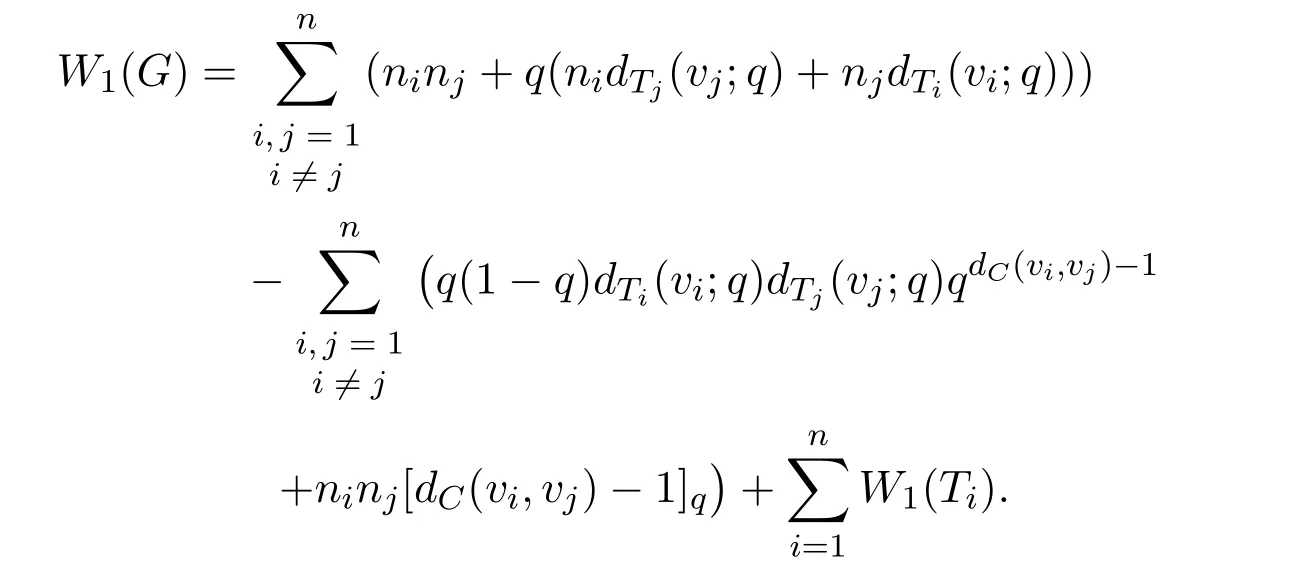
ProofAdd as few as possible edges to G such that in the new obtained graph G′,every vertex viis adjacent to every vertex vjwithFor every pair of vertices u∈V(Ti)and v∈V(Tj),we have

Combining this observation with the definition of dG(u,v;q),we have
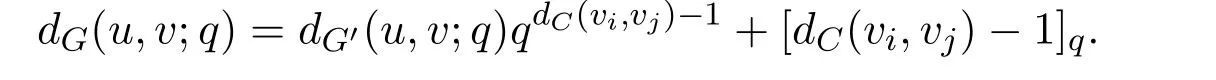
And so,

It follows from the combination of Lemma 2.1 and the above formula that

And so,the theorem follows.
As an application of Theorem 2.1,we shall present the explicity expression of the caterpillar cycles.This kind of graphs are constructed as follows[5].Let Ck=v1v2···vkv1be a cycle on k vertices with k ≥ 3.Then caterpillar cycle Ck(n1,n2···nk)is obtained from Ckby attaching nivertices to vi,where ni≥ 0 for all i=1,2,···,k.
Lemma 2.3[1,2]If n≥2,then

The following corollary follows directly from the combination of Theorem 2.1 and Lemma 2.3,and so we leave its proof to the readers.
Corollary 2.1Let Ck(n1,n2,···,nk)be a caterpillar cycle with k ≥ 3,ni≥0 for all i=1,2,···,k.If denote by C=v1v2···vkv1the unique cycle of this caterpiller cycle,and Tiby the tree of Ck(n1,n2,···,nk)−E(C)that contains vertex vi,then
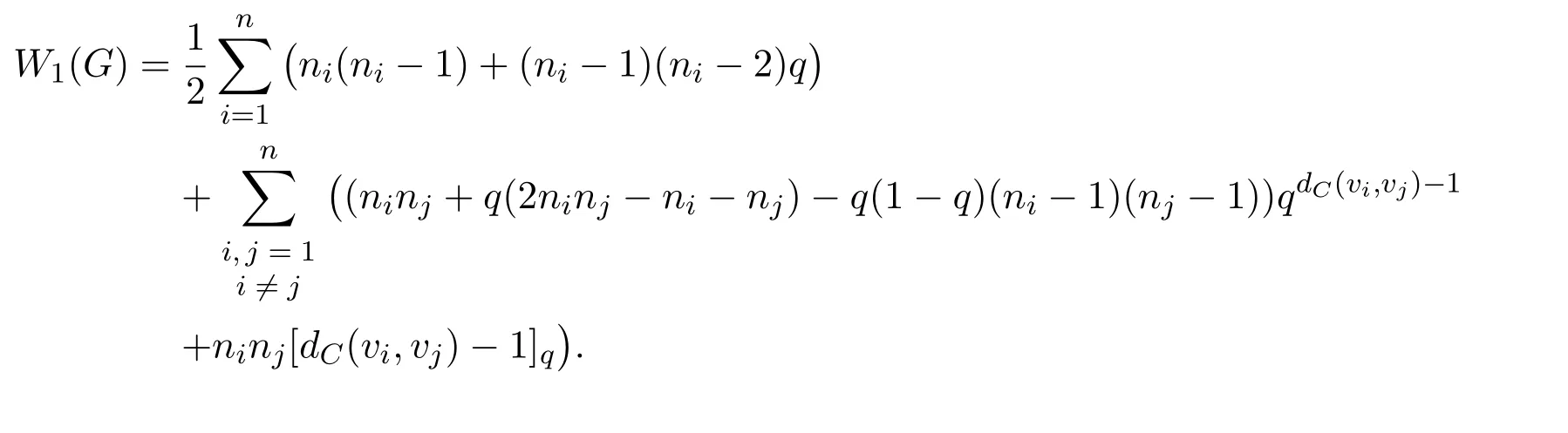
杂志排行
Annals of Applied Mathematics的其它文章
- SEMICLASSICAL LIMIT TO THE GENERALIZED NONLINEAR SCHRÖDINGER EQUATION∗†
- THREE KIRCHHOFFIAN INDICES OF THE CACTUS GRAPHS∗†
- SOME LIMIT PROPERTIES AND THE GENERALIZED AEP THEOREM FOR NONHOMOGENEOUS MARKOV CHAINS∗†
- EXISTENCE OF PERIODIC SOLUTION FOR A KIND OF THIRD-ORDER GENERALIZED NEUTRAL FUNCTIONAL DIFFERENTIAL EQUATION WITH VARIABLE PARAMETER∗
- PARALLEL COMPUTING METHOD OF PURE ALTERNATIVE SEGMENT EXPLICIT-IMPLICIT DIFFERENCE SCHEME FOR NONLINEAR LELAND EQUATION∗†
- ON THE CONDITIONAL EDGE CONNECTIVITY OF ENHANCED HYPERCUBE NETWORKS∗†
