SEMICLASSICAL LIMIT TO THE GENERALIZED NONLINEAR SCHRÖDINGER EQUATION∗†
2018-10-13BolingGuo
Boling Guo
(Institute of Applied Physics and Computational Math.,China Academy of Engineering Physics,Beijing 100088,PR China)
Guoquan Qin‡
(Graduate School of China Academy of Engineering Physics,Beijing 100088,PR China)
Abstract In this paper,we investigate the semiclassical limit of the generalized nonlinear Schrödinger equation for initial data with Sobolev regularity.Also,we will analyze the structure of the fluid dynamical system with quantum effect corresponding to the semiclassical limit of the generalized nonlinear Schrödinger equation.
Keywords quantum hydrodynamics;dispersive limit;compressible Euler equation
1 Introduction
Hydrodynamics equations with quantum effect describe the hydrodynamical properties and states of some important physical phenomena such as semiconductor,superconductor and super flow.This kind of equations have theoretical significance and practical value.From the semiclassical limit of the nonlinear Schrodinger(NLS)equation with Plank constant h,we can derive various hydrodynamics equations with quantum effect when h→0.
It is well known that the quantum hydrodynamics equations(QHD)can be derived based on the moment method,which is analogous to the derivation of the compressible Euler equation from the Boltzmann equation by taking the zeroth,first and second order velocity moments of the quantum Boltzmann equation and resulting in a hydrodynamical model which then has to be closed in an approximate way,that is,a reasonable macroscopic approximation for the quantum heat flow tensor has to be derived by using additional(quantum)physical properties of the particle ensembles.Moreover,in the case of high electric fields,small mean-free-path asymptotics have been used to derive QHD-models.
When the time and distance scales are large enough relative to the Plank constant h,the system will approximately obey the laws of classical,Newtonian mechanics.That is,quantum mechanics becomes Newtonian mechanics as h→0.The asymptotics of quantum variables as h→0 are known as semiclassical expressing this limiting behavior.
In the semiclassical limit or WKB limit and when ∇xand ∂tscale like ϵ as ϵ→ 0(ϵ is the scaled Planck constant),the quantum-mechanical pressure becomes negligible.The isentropic compressible Euler equation can be formally recovered from the nonlinear Schrödinger equation in this limit.This fact was proven rigorously by Jin,Levermore and McLaughlin[5,6]for the one-dimensional integrable case using the inverse scattering technique and by Grenier[3]for higher dimensions in situations where no vortices are involved.
Very similar model equations have been used for quite a while in other areas of theoretical and computational physics,for instance,in super fluidity[11,12]and in superconductivity[2].
2 Semiclassical Limit to the Nonlinear Schrödinger Equation in Short Time Range
In this section,we consider the following nonlinear Schrödinger(NLS)equation with rapidly oscillating data
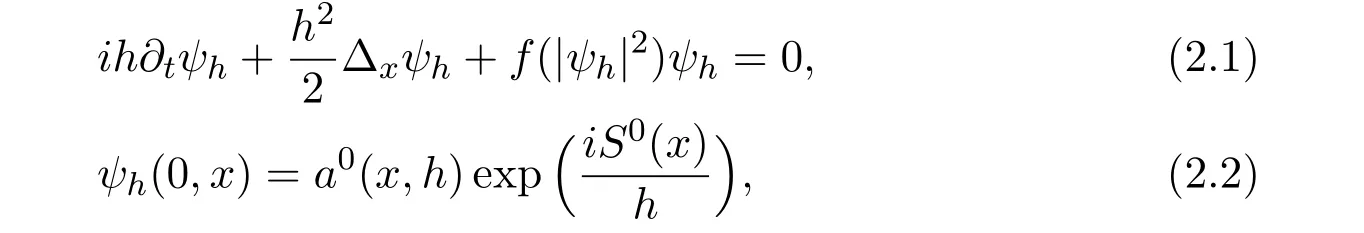
where f∈C∞(R+,R),S0(x)∈Hs(Rd)for s large enough.And a0is a function,polynomial in h with coefficients of Sobolev regularity in x.h is the Plank constant and ψhis the wave function.
We will study the semiclassical limit of equation(2.1)-(2.2)and determine the limiting dynamics of any function of the field ψhas h → 0.
Remark 2.1When f(x)=x,equation(2.1)appears in the phenomenological description of super fluidity of an almost ideal Bose gas[10].In this case,the squared modulus of the wave function ψ¯ψ is interpreted as the particle number density in the condensate state,while the gradient of the phase is proportional to the super fluid velocity u= ∇argψ.Moreover,the nonlinear Schrödinger equation is very helpful for the mathematical analysis of the isentropic irrotational QHD-system[4–6,15].
Employing the WKB method,we will look for the solution to(2.1)-(2.2)having the following form

where

and aj(x,t)satisfies certain equations so that we could solve(2.1)locally in time.
Let

then(2.1)is transformed to

The above equation is a perturbation of the following isentropic compressible Euler equation
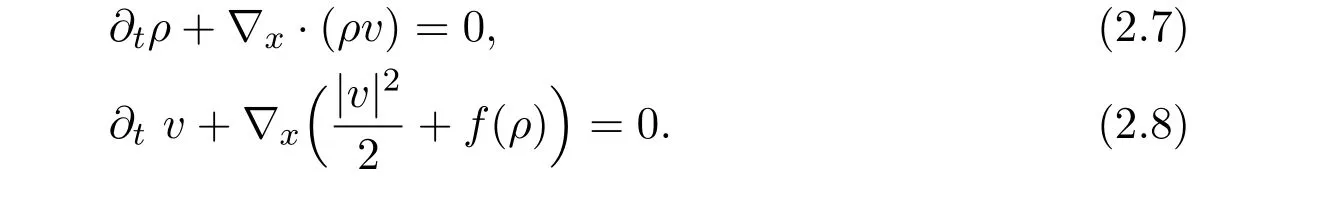
If f′>0,then equation(2.7)-(2.8)admits a local smooth solution in[0,T∗]for T∗sufficiently small.In fact,we have the following theorems.
Theorem 2.1SupposeHs(Rd)and a0(x,h)be uniformly bounded in Hs(Rd)with respect to x.Then there exists a constant T >0 such that equation(2.1)-(2.2)admits a solution ψh=ah(x,t)exp(iSh(x,t)/h),where ahand Share bounded in L∞([0,T];Hs).
Theorem 2.2Under the assumption of Theorem 2.1,assume further a0(x,h)as h → 0 and equation(2.7)-(2.8)with initial data(ρ(0,x),v(0,x))=admits a solution.Then,equation(2.1)admits a formal solution ψh(x,t)=ah(x,t)exp(iSh(x,t)/h)on[0,T]satisfying the initial condition(2.2)for h small enough,where ahand Share uniformly bounded in L∞([0,T],Hs)with respect to h.
Theorem 2.3Under the assumption of Theorem 2.2,if a0(x,h)admits the following expansion
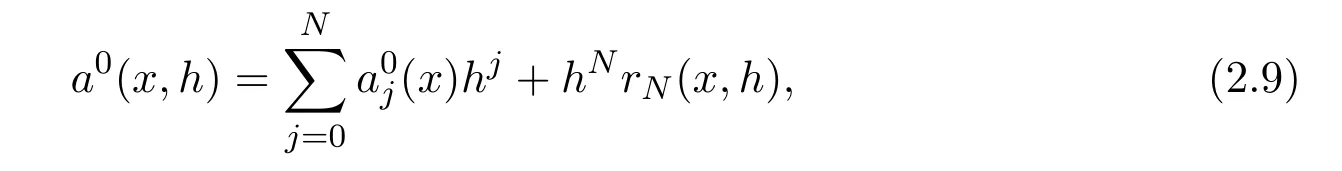
where N∈N,s−2N−2−d/2>0 and rNsatisfy

Then for interval[0,T]given in Theorem 2.2,one has as h→0
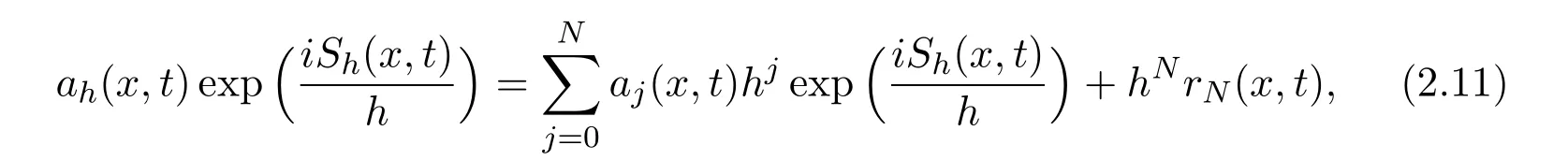
where S and ajare determined by the WKB method and

Proof of Theorem 2.1Suppose
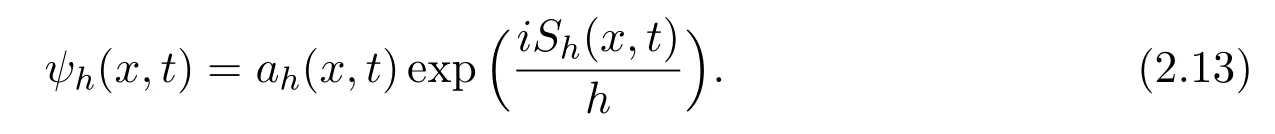
Substituting(2.13)into(2.1)yields

which can be rewritten as
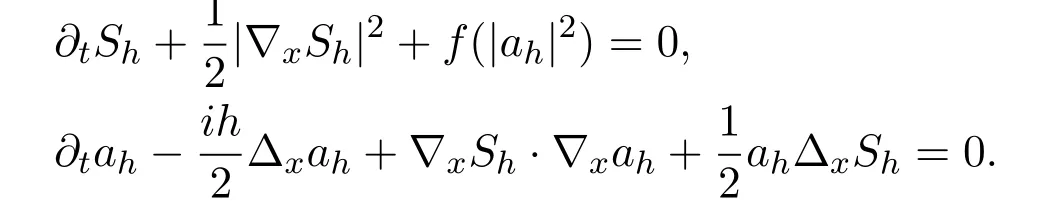
Setting ωh= ∇xSh,we have

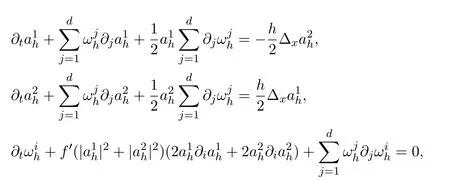

where

The matrix A(uh,ξ)can be symmetrized for f′>0 by


with S symmetry.
For the first term,we have

Since
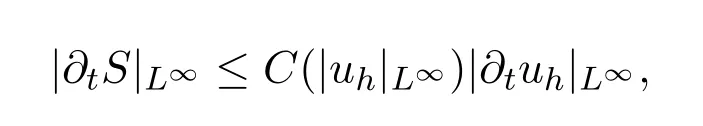
employing the Sobolev embedding and the equation(2.14)yield

For the second term,one easily obtains

Using integration by parts leads to

The second term on the right hand side of(2.15)can be written as
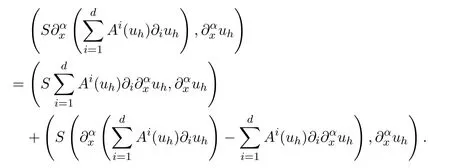
Invoking the symmetry of SAi(uh)yields

therefore,one finds

By the commutator estimates,there holds

Consequently,we find

Proof of Theorem 2.2Assume there exists a solution(ρ,v) ∈ L∞([0,T],Hs+2(Rd))of(2.7)-(2.8)on[0,T]withand the initial condition

We will prove there exists a solution of(2.14)in a interval[0,T)with T independent of h for h small enough and the solution is uniformly bounded in L∞([0,T];Hs).The formal limit of equation(2.14)is

where u=(a1,a2,ω)admits a solution in the maximal interval[0,T′]with T′≥ T.Set vh=uh−u,then we find
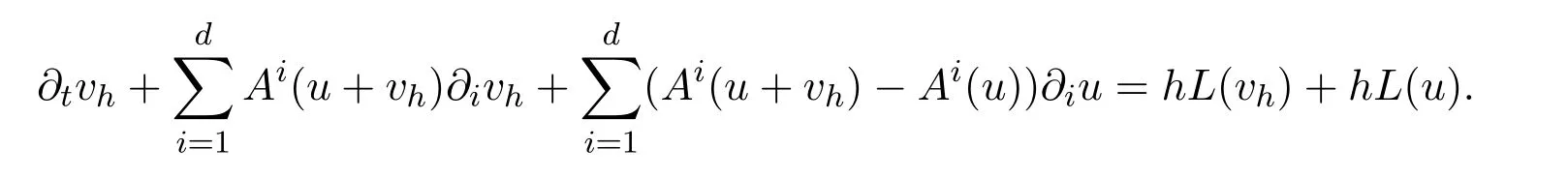

Note that
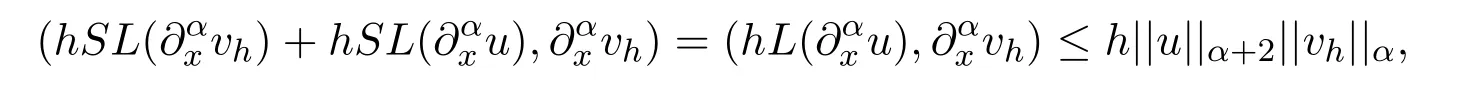
so
When she got to the outskirts24 of the town, led by the light of the moon, she met a fox, who offered to accompany her, an offer which Grannonia gladly accepted, saying You are most heartily25 welcome, for I don t know my way at all about the neighbourhood

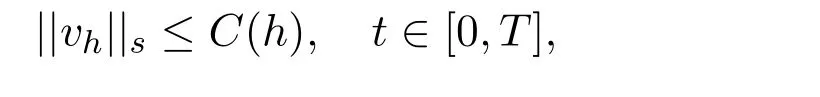
where C(h)→0 and h→0.We thus complete the proof of Theorem 2.2.
Proof of Theorem 2.3We prove the theorem in four steps.
1.Zero order approximation
From Theorem 2.2,we know that ahand ωhare uniformly bounded in L∞([0,T];Hs(Rd)).Therefore, ∂tahand ∂tωhare bounded in L∞([0,T];Hs−2(Rd)). We can extract subsequences of ahand ωhconverging toand,respectively in L∞([0,T];Hs−2(Rd))and the limits are the unique solution of

2.First order approximation
Let vh=uh−u,we can prove the following energy estimates
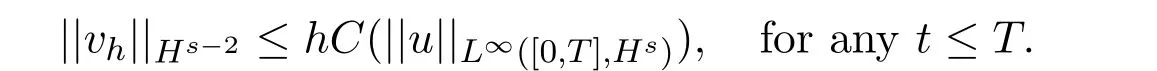
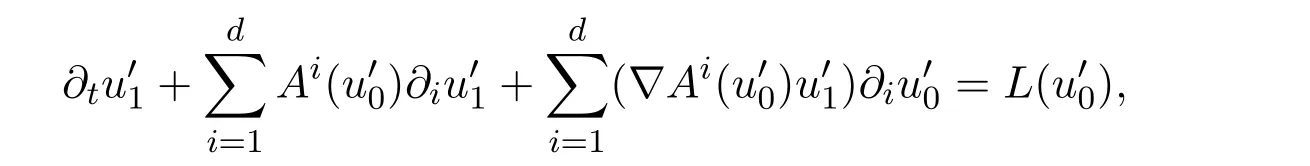
and the initial condition
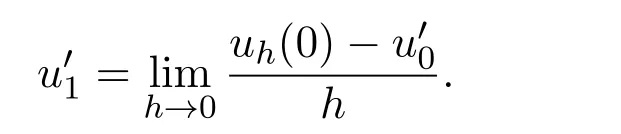
The solution to this problem is unique.In fact,there exists a subsequence of evhconverge to
3.Higher order approximation
Assume the N-th approximation to be
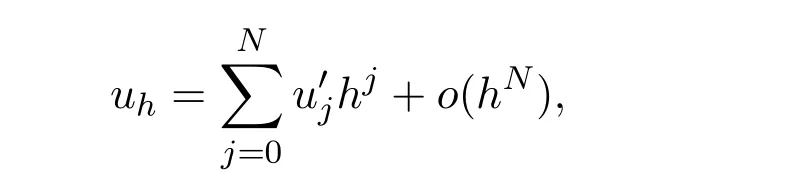
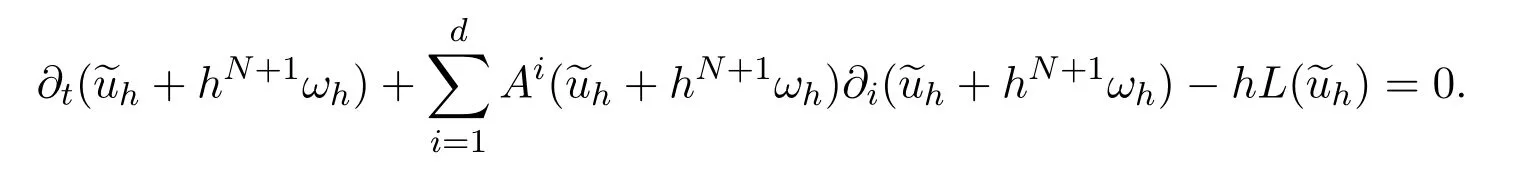
4.WKB expansion
We have expanded the formal solution ahand Shto any order.To return to the WKB expansion,one can write the following two formal series

3 Semiclassical Limit to the Derivative Schrödinger equation
Now,let us consider the following derivative Schrödinger equation(GDNLS)

where f∈C∞(R+,R),S0∈Hs(R)for s large enough,is a polynomial in h with coefficients of Sobolev regularity in x.We consider the limit of(3.1)-(3.2)when h→0,for−∞ When f(x)=x in equation(3.1),the resulting equation is used to describe the nonlinear propagation of magnetosonic wave trains parallel to the magnetic field in a hot or collisionless ideal plasma with dispersion due to Hall currents[7,13]. Introducing the new variables ρ =A2=|ψ|2,u=Sx,we have where Thus,equation(3.5)-(3.6)can be regarded as a perturbation to the following compressible Euler equation Multiplying(3.6)by ρ and using(3.5)lead to where µ = ρu is the momentum and P′(ρ)=2ρf′(ρ)= ρΦ′(ρ).From(3.5),using P(ρ)= ρΦ′(ρ)− Φ(ρ),one finds or where Thus,there holds Adding(3.10)and(3.12)leads to As in[1],we denote by M= µ+Φ(ρ)the noncanonical momentum.Using Q(ρ)=equation(3.5)-(3.6)can be written as and this can be rewritten as the local conservation laws of ρ,M,Φ Collecting the above arguments,we obtain the following theorem. Theorem 3.1Equation(3.1)is equivalent to the dispersive perturbation of the quasilinear hyperbolic equation(3.14)-(3.15)or(3.16)-(3.17).The density ρ and the noncanonical momentum M are the conserved quantities of the GDNLS equation.In particular,whenand,(3.16)-(3.17)is equivalent to In addition,we will prove the following theorem. Theorem 3.2Let∗be the complex conjugate.The GDNLS equation admits the following conserved quantities where the fluid dynamical variablescan be represented by the wave function ψ as ProofObviously,the theorem can be deduced directly by(3.14)-(3.15).Here,we will derive it from(3.1)and thus we can better understand the relation between the classical mechanics and the quantum mechanics. Note that we have the following equality Because the third term in(3.26)only depends on ψψ∗=|ψ|2,we can integrate it with respect to x to obtain This proves(3.20). Also,one easily deduces Subtracting(3.28)from(3.29),we obtain Next,note that the following equality is equivalent to(3.5)-(3.6)with Integrating(3.31)yields Multiplying(3.28)by Φ′(ρ)leads to Adding(3.30)and(3.34)and using we obtain which leads to This complete the proof. For the GDNLS equation with the initial condition where the amplitude A0(x)is nonnegative,the phase S0(x)is real-valued and smooth and is independent of h.One can take We can prove that ψhis a dispersive perturbation with O(h2)error as h → 0 to the following deformed Euler equation with the initial condition Consider Then(3.18)-(3.19)can be transformed to From we have On the other hand with Consequently,one obtains the energy equation Assume f(ρ)= ρ,then the Euler equation derived by the semiclassical limit is with initial data Energy equation(3.52)is then One can rewritten(3.54)-(3.55)as with The eigenvalues of B are the roots of or the corresponding right and left eigenvector are respectively The Riemann invariants is The eigenvalues λ+,λ−can be represented by the Riemann invariants as The equation can be rewritten by the Riemann invariants as with initial data Theorem 3.3The blowup time tbcan be estimated as with where and x±(t)satisfying ProofThe break-time tbcan be estimated by Laxs recipe[8,14]. From(3.65),we obtain Similarly, Differentiating(3.68)with respect to x and setting Z+=∂xR+,we obtain (3.69)leads to Therefore Substituting(3.72)into(3.70)yields one can derive the standard Raccati equation The solution to(3.75)is where The integration is along the characteristic of λ+and the sign of q0K(t)impact its singularity essentially.If the initial data satisfiesnamely,q0<0,then q+(x,t)will tend to infinity in finite time,which implies that q+(x,t)certainly will blowup and 1+q0K(t)=0.Therefore,the blowup time tbcan be estimated as follows. Let t+,bsatisfy with The particle trajectory x=x+(t)satisfies Similarly,to estimate t−,b,we consider the characteristic of.When f(ρ)= −ρ,we have and the energy equation is (3.77),(3.78)can be write as a matrix form as follows where of which the eigenvalues are the roots of that is, then the corresponding eigenvector are The Riemann invariants are The equation can be written as with the initial data This completes the proof. Similarly,we can derive the estimate of the blowup time Theorem 3.4The blowup timecan be estimated as where and Consider the generalized NLS Setting one obtains where When ϵ=0,the MNLS is where we define the sonic We consider the inverse scattering method to MNLS. To do so,we first consider the initial condition of(4.6), Assume ρ0(x)andare real-valued Schwartz functions for x ∈ R and In particular,choose u0(x)and S0(x)as where S0(0),δ and µ are real-valued parameters andTherefore, Without loss of generality,let ν=1,S0(0)=0. When ν =1,Q in the definition of(4.7)becomes In the transonic domain,Q(x)will necessarily change sign.From(4.12),it is easy to see that Q(x)is a quadratic equation of T(x)and has two roots.For simplicity,suppose T has only one root for T ∈ (−1,1).For this,assume and According to inequalities(4.13)-(4.15),(4.12)has a unique solution in(−1,1), Consequently,when t=0,x Theorem 4.1Let ϕϵ(x,t)be a solution of Cauchy problem to the MNLS equation(4.1)with the initial data(4.3),where A0(x)and S0(x)are given by(4.10).Then there exists a smooth curve x=xc(t),t≥ 0,xc(0)=xc,such that for all t≥ 0 and x ProofWe use Riemann-Hilbert method to solve this problem.Assume the unknown matrix M(k;x,t)admits a discontinuous matrix in the complex plane, where are the Pauli spin matrices. where r(k)= −r(−k)is the reflection coefficient,and Then the solution to the MNLS equation can be derived from M(k;x,t) We thus complete the proof. Remark 4.1Here,the error term holds uniformly in any compact subset of(x,t).A(x,t)and S(x,t)are smooth real-valued functions,independent of ϵ and satisfy A(x,0)=A0(x)and S(x,0)=S0(x).When x satisfy the MNLS equation(4.6).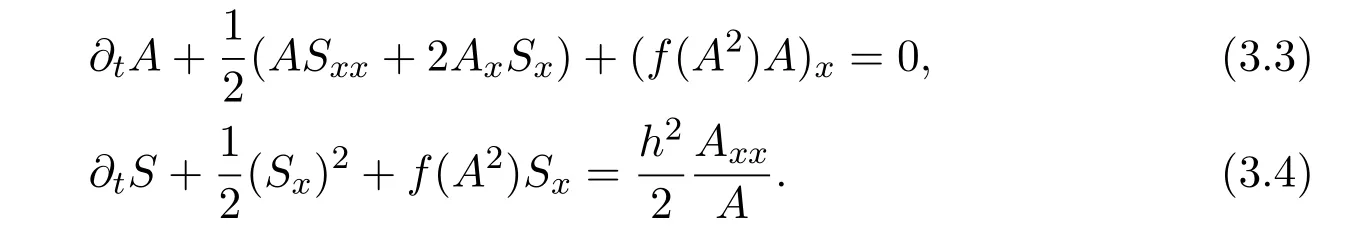

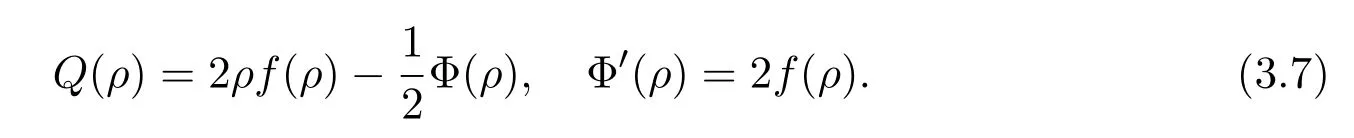
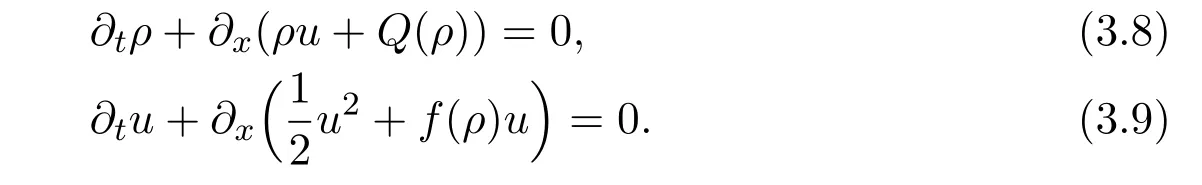

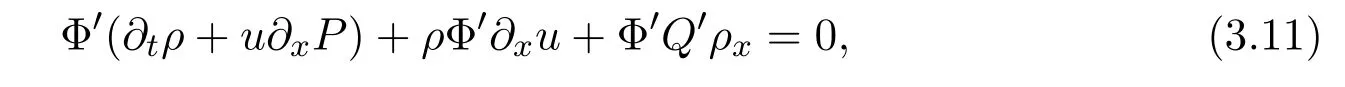
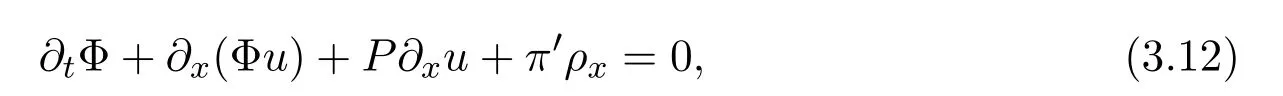


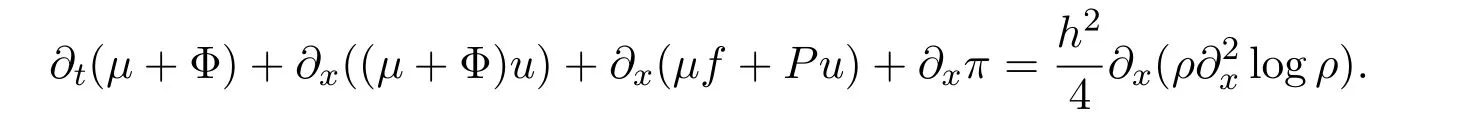
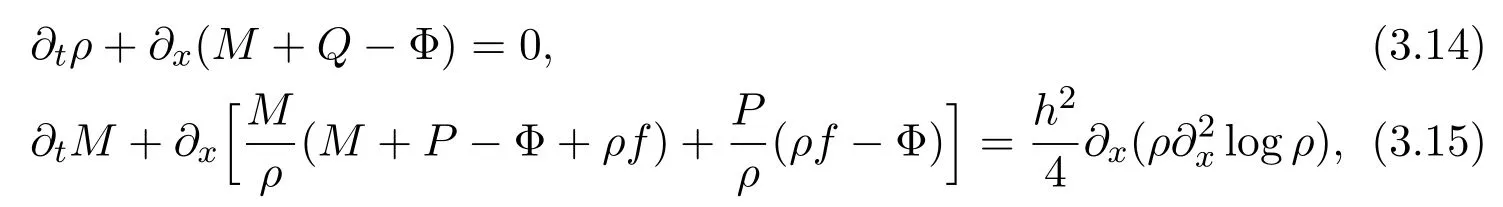
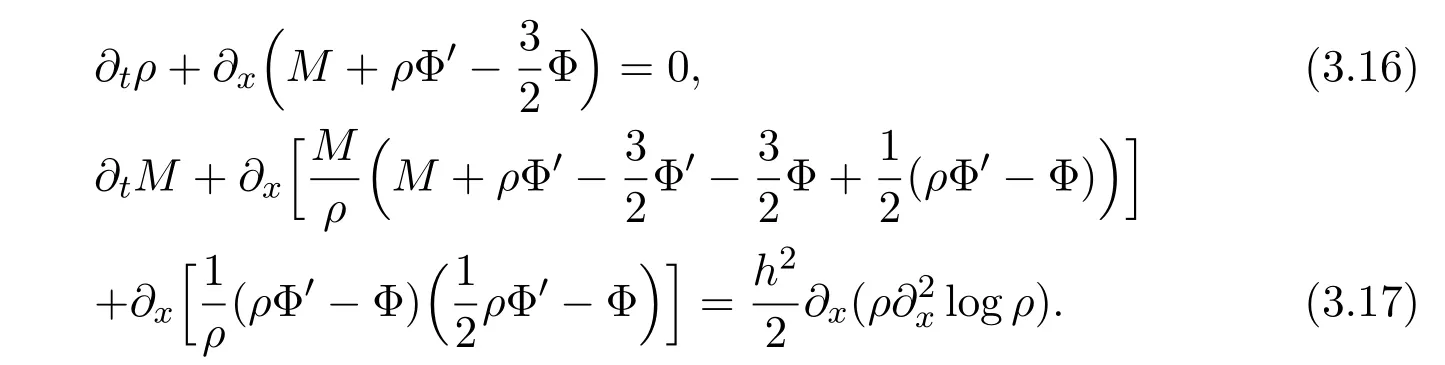
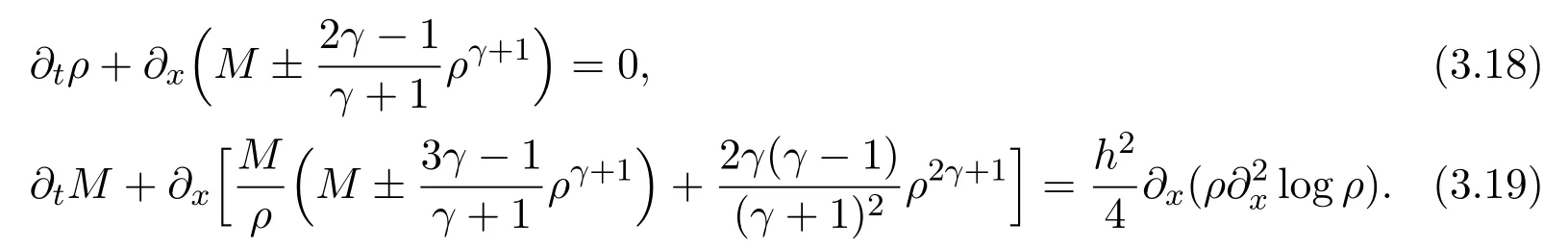

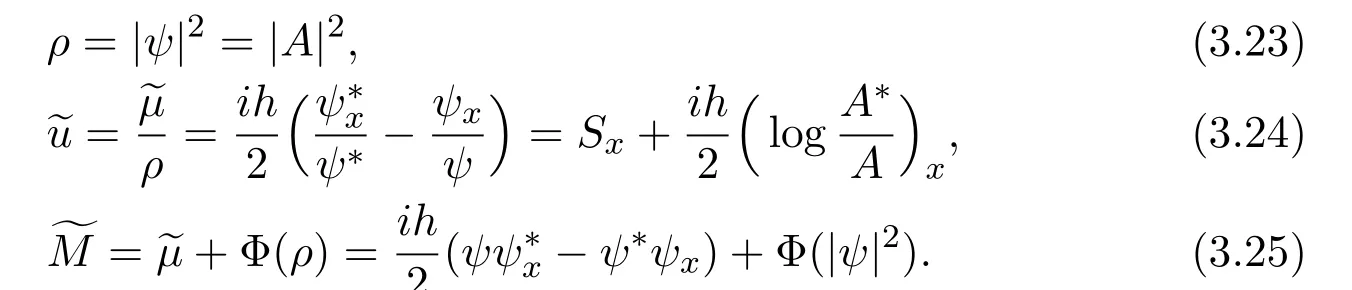


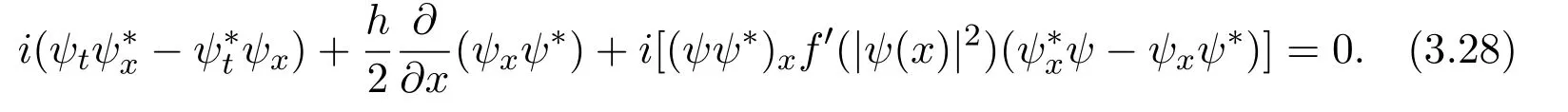
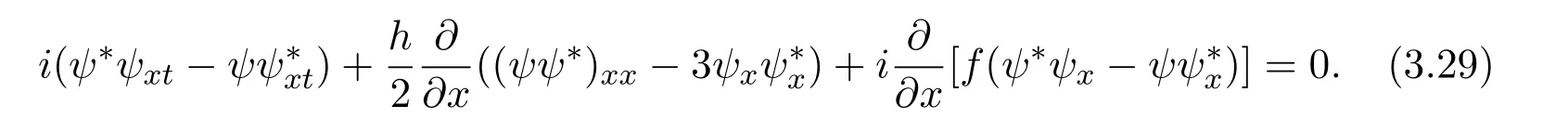


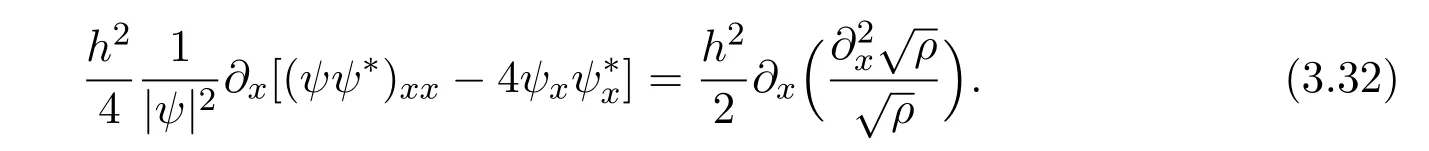

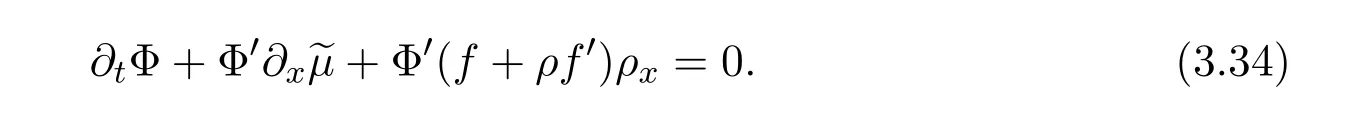






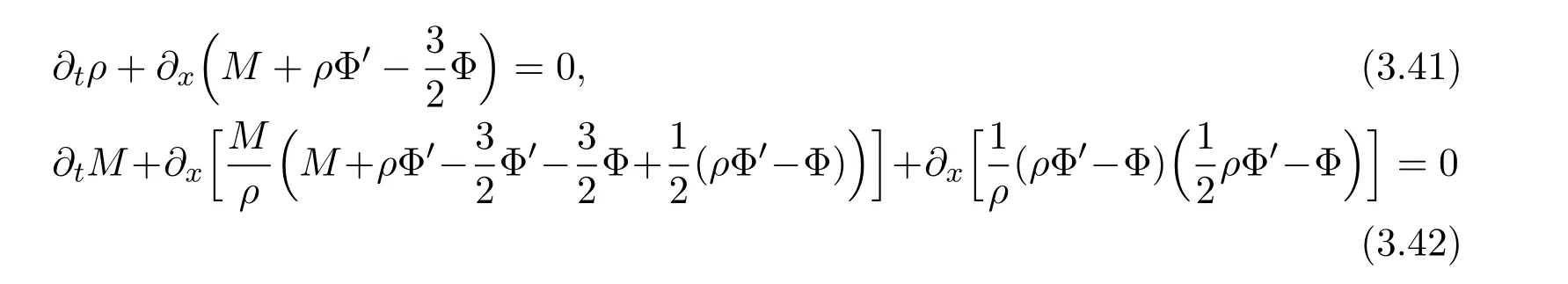
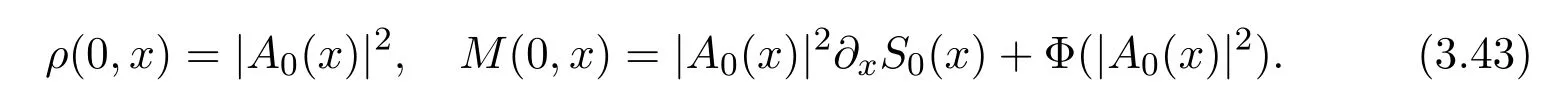


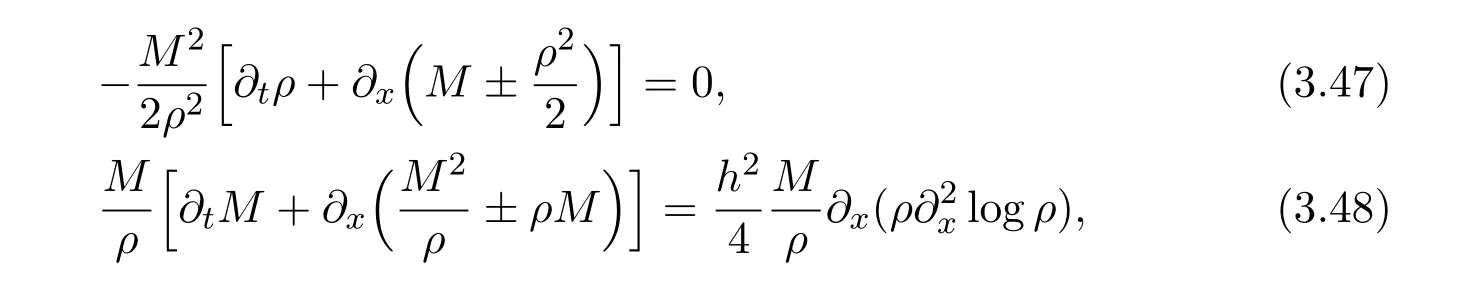

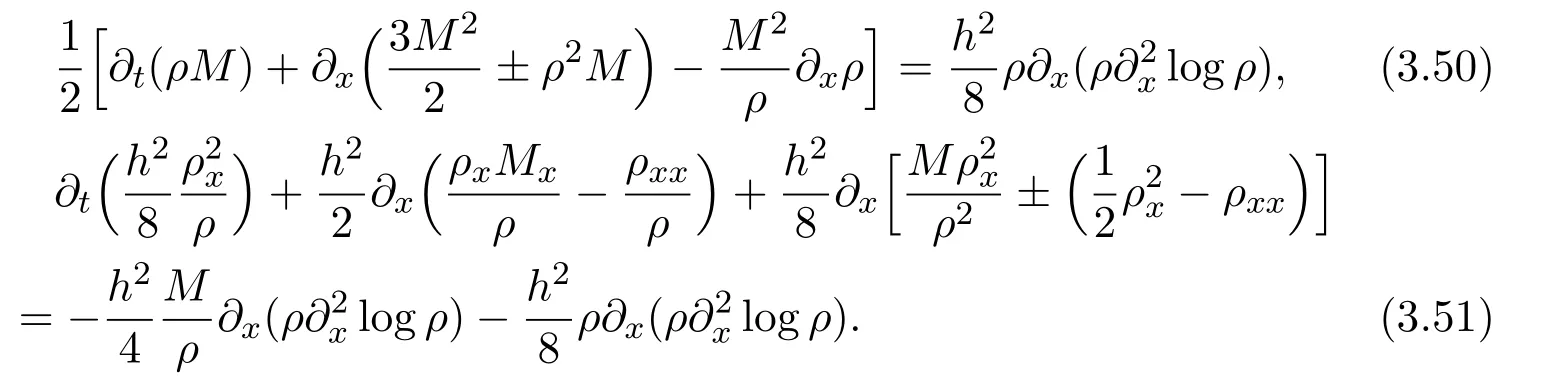
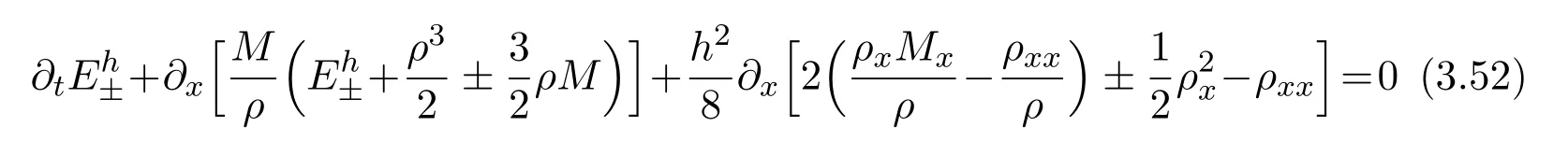
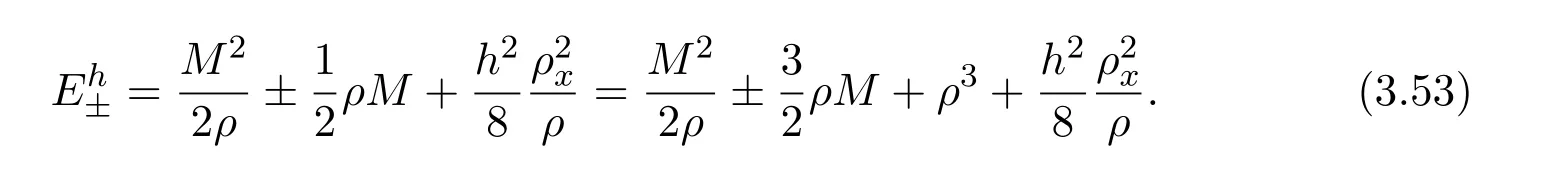





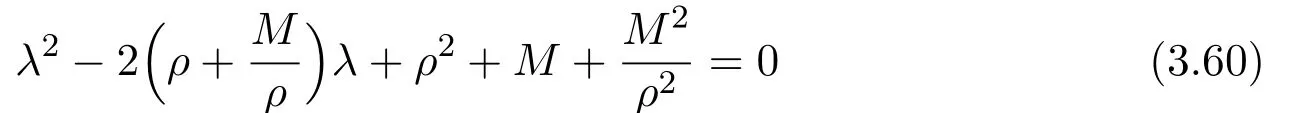

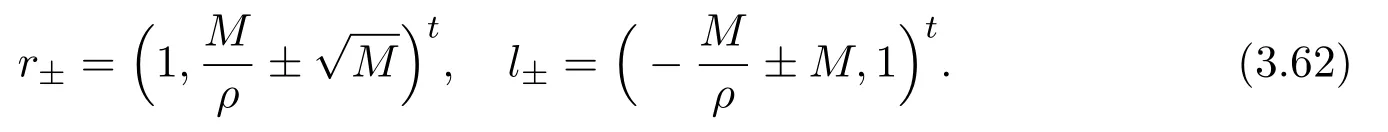

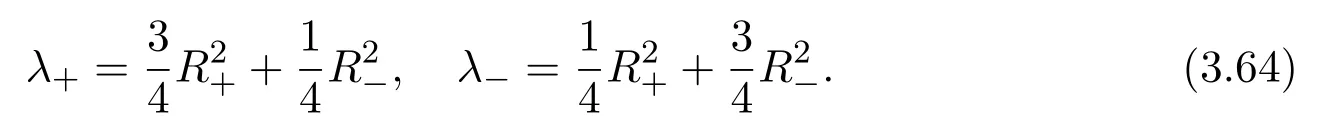


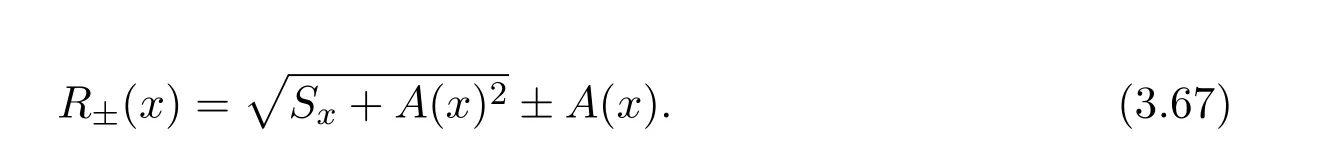

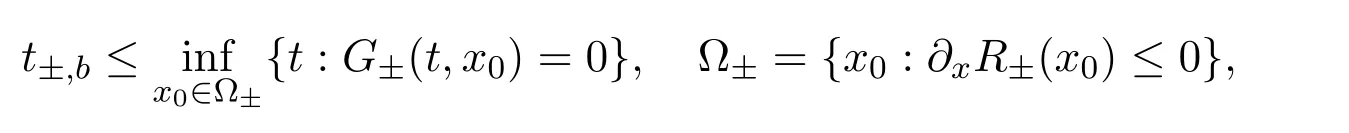
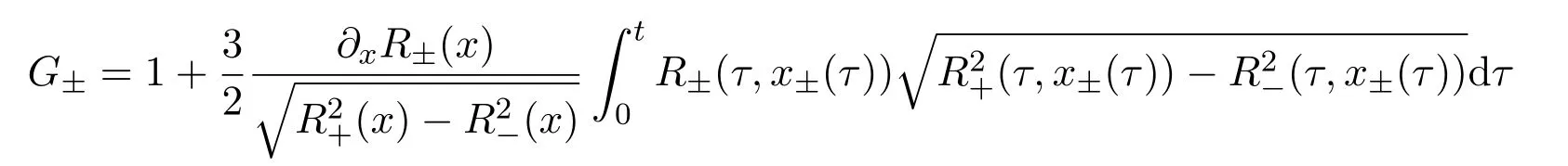


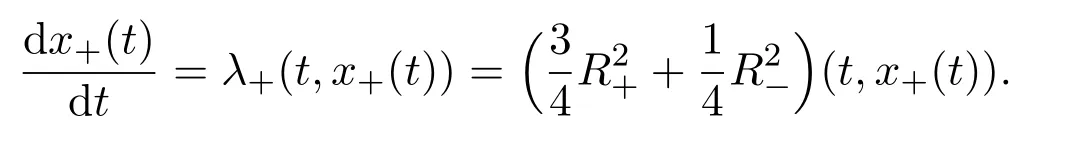
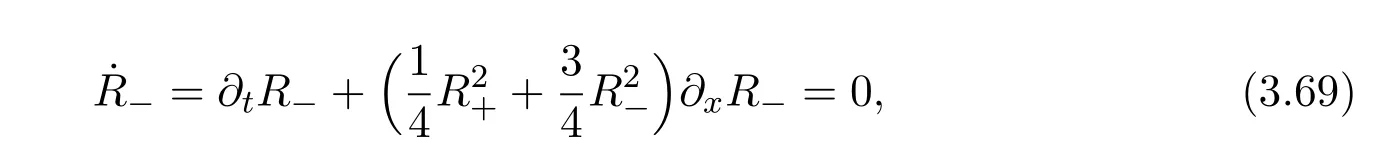
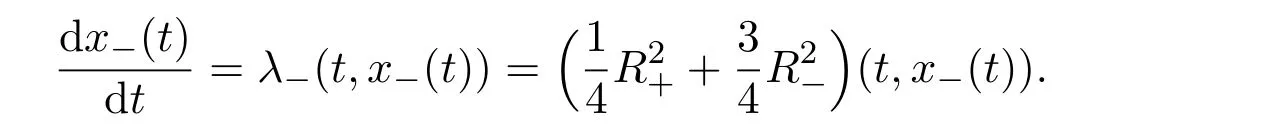





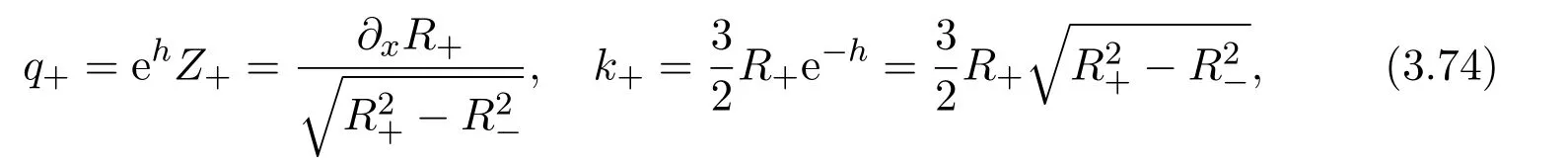


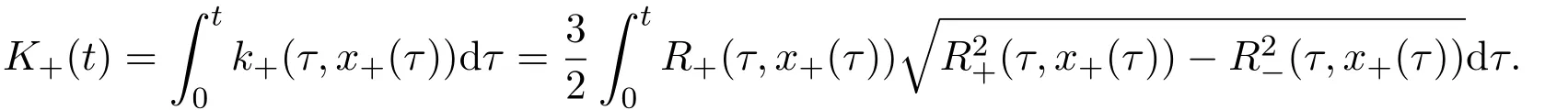
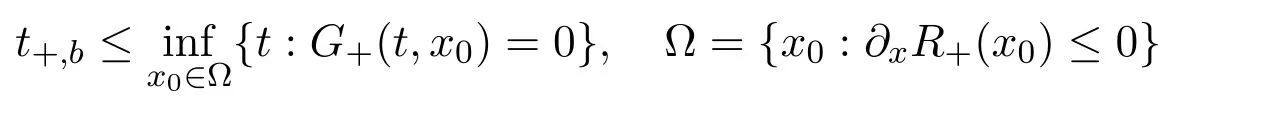
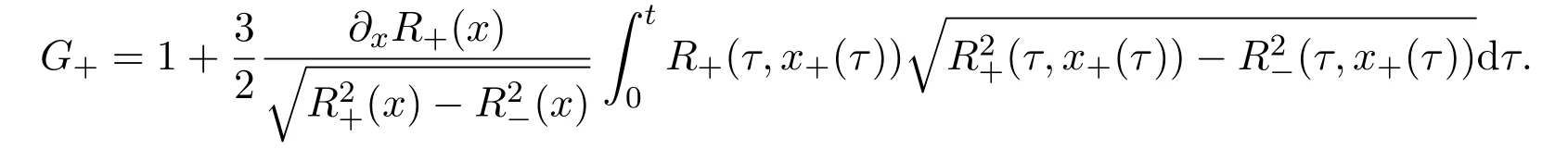
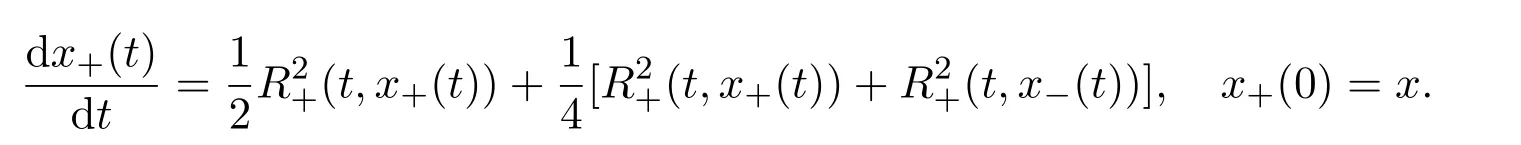

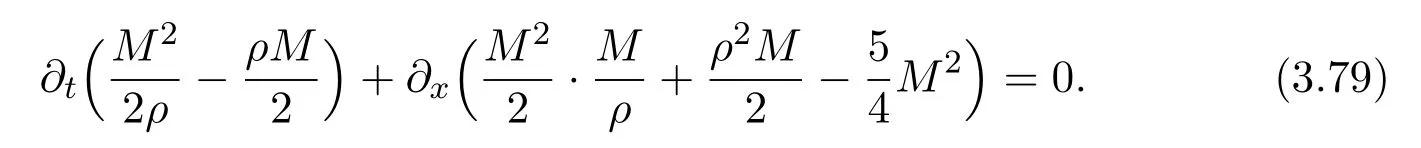
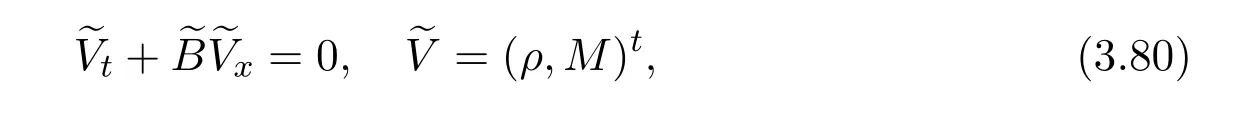
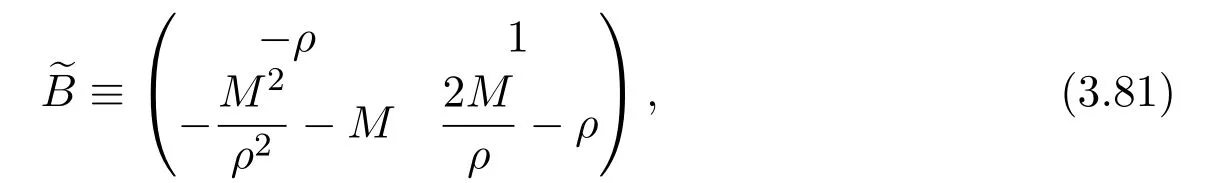






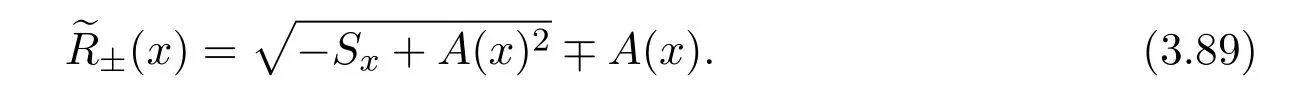


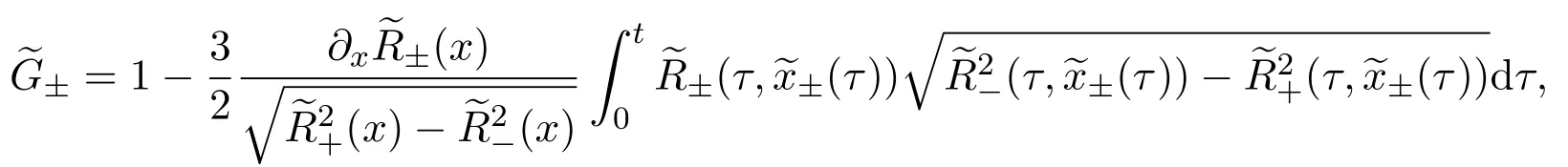
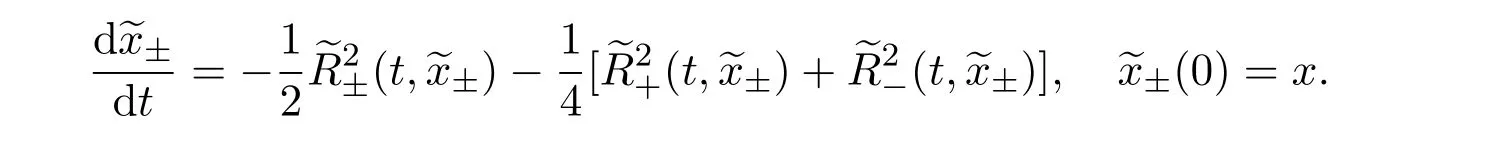
4 Semiclassical Limit to the Generalized NLS:Subsonic,Supersonic,Transonic
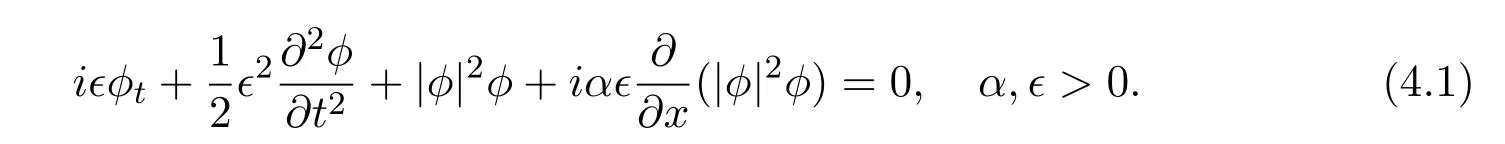








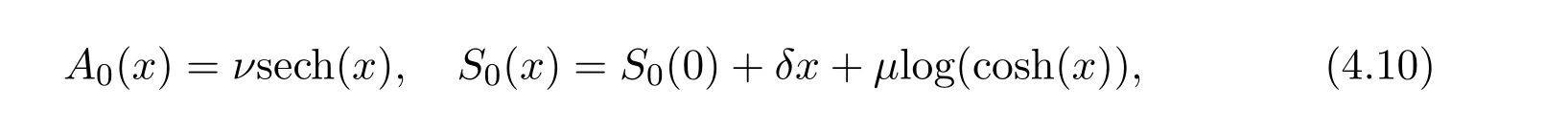

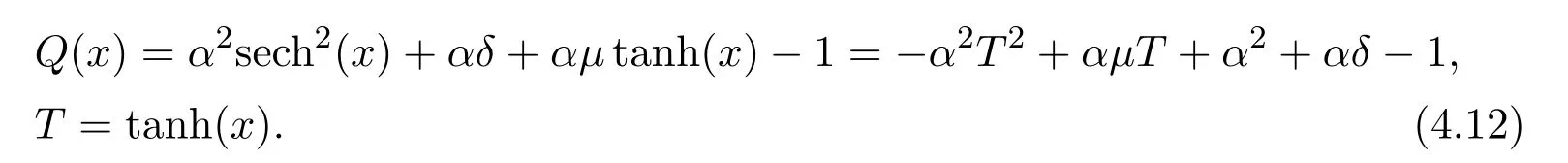




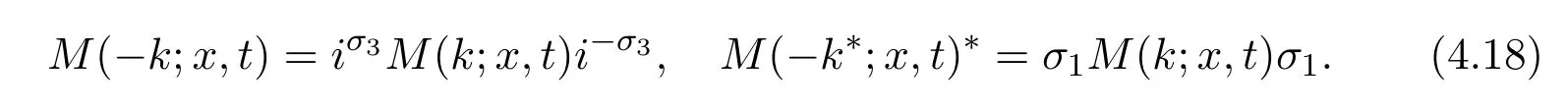
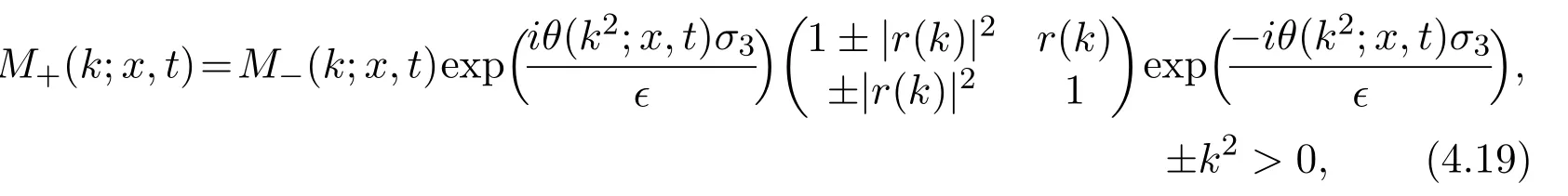





杂志排行
Annals of Applied Mathematics的其它文章
- THREE KIRCHHOFFIAN INDICES OF THE CACTUS GRAPHS∗†
- ON q-WIENER INDEX OF UNICYCLIC GRAPHS∗†
- SOME LIMIT PROPERTIES AND THE GENERALIZED AEP THEOREM FOR NONHOMOGENEOUS MARKOV CHAINS∗†
- EXISTENCE OF PERIODIC SOLUTION FOR A KIND OF THIRD-ORDER GENERALIZED NEUTRAL FUNCTIONAL DIFFERENTIAL EQUATION WITH VARIABLE PARAMETER∗
- PARALLEL COMPUTING METHOD OF PURE ALTERNATIVE SEGMENT EXPLICIT-IMPLICIT DIFFERENCE SCHEME FOR NONLINEAR LELAND EQUATION∗†
- ON THE CONDITIONAL EDGE CONNECTIVITY OF ENHANCED HYPERCUBE NETWORKS∗†
