ON THE CONDITIONAL EDGE CONNECTIVITY OF ENHANCED HYPERCUBE NETWORKS∗†

Yanjuan Zhang,Hongmei Liu,Dan Jin

(College of Science China Three Gorges University,Yichang 443002,Hubei,PR China)

Abstract Let G=(V,E)be a connected graph and m be a positive integer,the conditional edge connectivityis the minimum cardinality of a set of edges,if it exists,whose deletion disconnects G and leaves each remaining component with minimum degree δ no less than m.This study shows that for n-dimensional enhanced hypercube Qn,k.Meanwhile,another easy proof aboutfor n≥3 is proposed.The results of enhanced hypercube include the cases of folded hypercube.

Keywords interconnected networks;connectivity;conditional edge connectivity;fault tolerance;enhanced hypercube

1 Introduction

A multiprocessor system may contain numerous number of nodes,some of which may be faulty when the system is implemented.Reliability and fault tolerance are two of the most critical concerns of multiprocessor systems.Based on the definition proposed by Esfahanian[1],a multiprocessor system is fault tolerance if it can remain functional when failures occur.Two basic functionality criteria have received many attention.The first one is whether the network logically contains a certain topological structure.This problem occurs when embedding one architecture into another.This approach involves system wide redundancy and reconfiguration.The second functionality criterion considers a multiprocessor system function if a faultfree path exists between any two fault-free nodes.Hence,connectivity and edge connectivity are two important measurements of this criterion[2].A vertex cut of a connected graph G is a set of vertices whose removal disconnects G.The connectivity κ(G)of a connected graph G is the cardinality of a minimum vertex cut.An edge cut of a connected graph G is a set of edges whose removal disconnects G.The edge connectivity λ(G)of a connected graph G is the cardinality of a minimum edge cut[3].However this two parameters may result in an isolated vertex.This is practically impossible in some network applications.To address this deficiency,many specific terms forbidden fault set and forbidden fault edge set are introduced such as conditional connectivity[4],extra connectivity and extra edge connectivity[5].

The n-dimensional hypercube Qnis one of the most versatile and efficient interconnected networks because of its regular structure,small diameter,and good connection with a relative small node degree[2],all of which are very important for designing parallel systems.As the importance of hypercubes,many variants of Qnhave been proposed,among which,for instance,are crossed hypercube,argument hypercube,folded hypercube and enhanced hypercube.As an enhancement on the hypercube Qn,the enhanced hypercube Qn,kproposed by Tzeng and Wei[6],not only retains some of the favorable properties of Qn,but also improve the efficiency of the hypercube structure,since it possesses many properties superior to hypercube[7-9].For example,the diameter of the enhanced hypercube is almost half of the hypercube.The hypercube is n-regular and n-connected,whereas the enhanced hypercube is(n+1)-regular and(n+1)-connected.Its special case of k=1 is the well-known Folded hypercube(denoted by FQn),which has been used as underlying topologies of several parallel systems,such as ATM switches[10,11]PM2I networks[12],and 3D-FoIHNOC networks[13]for high-speed cell-switching and reducing the diameter and traffic congestion of the hypercube with little hardware overhead.

The conditional edge connectivitywhich is the generalization of edge connectivity,is defined as the cardinality of the minimum edge cut,if it exists,whose deletion disconnects G and leaves each component with minimum degree δ no less than m.Xu[2]providedandObviously,Paper[14]made a good job on the conditional edge connectivity of Qnand proved thatfor n ≥ 2,for n ≥ 3 andfor n ≥ 4.However there is nothing about the conditional edge connectivity of enhanced hypercube.In this paper,we discuss the properties of enhanced hypercubes Qn,kand show thatfor n ≥ 3 which includes the results of folded hypercube.Meanwhile,this paper proposes an easy proof offor n≥3.

2 Preliminaries

The graph theoretical definitions and notations follow[2].A network is usually modeled by a connected graph G=(V,E),where V and E represent the vertex and edge sets of G=(V,E)respectively.G is bipartite if V can be partitioned into two subsets V1and V2,such that every edge in G joins a vertex of V1with a vertex in V2.A bipartite graph is bipancyclic if it contains a cycle of every even length from 4 tothenis a bipartition.A graph is said to be pancyclic if it contains a cycle of every length from 3 to|V(G)|.Two graphs G1and G2are isomorphic,denoted asif there is a one to one mapping f from V(G1)to V(G2)such that(u,v)∈E(G1)if and only if(f(u),f(v))∈E(G2).Two vertices which are incident with a common edge are adjacent.As are two edges which are incident with a common vertex.A path is a sequence of adjacent vertices,with the original vertex v0and end vertex vm,represented as P(v0,vm)=(v0,v1,v2,···,vm)where all the vertices v0,v1,v2,···,vmare distinct except that possibly the path is a cycle when v0=vm.A cycle is called a Hamiltonian cycle if it traverses every vertex of G exactly once.Two paths are internode disjoint if and only if they don’t have any vertices in common.If u,v∈V(G),d(u,v)denotes the length of a shortest path between u and v.The diameter of G is defined as diam(G)=max{d(u,v):u;,v∈V(G)}.Letbe a subset of V,G[V1]=(V1,E1)is an induced subgraph by V1such that for any edgeif and only ifis an induced subgraph by deleting both of all vertices in V1and all edges incident with vertices in V1,whereLetbe a subset ofis a subgraph induced by F satisfying x∈ V′if and only if x being incident with some edges ofis a subgraph obtained by deleting all edges of F.For X,Y⊂V,denote by[X,Y]the set of edges of E(G)with one end in X and the other in Y,certainly,[X,Y]is an edge cut of graph G.

An n-dimensional hypercube denoted by Qnhas 2nvertices,and has vertex set V(Qn)={x1x2···xn:xi=0 or 1,1 ≤ i≤ n},with two vertices x1x2···xnand y1y2···ynbeing adjacent if and only if they differ in exactly one bit.Let x and y be two vertices of hypercube Qn,dQn(x,y)be the length of the shortest path between vertices x and y in hypercube Qn.The Hamming distance between x and y,denoted by h(x,y),is the number of different bits between the corresponding strings of x and y,that is the length of the distance of the shortest path between the x and y in Qn.Obviously,by the definition of Hamming distance,we know thatwhere dQn(x,y)is the shortest path between the vertex x and node y in Qn.The Hamming weight of a vertex x is defined asso whether a vertex is even or odd,bases on whether the hamming weight of the vertex is even or odd.In this paper,if we denote the nodethenfor some i∈{1,2,···,n},in other words,the binary strings of the two vertices x and xiis different exactly on the ith position.And the edge(x,xi)represents the i-dimensional hypercube edge in Qn.The set of i-dimensional edges is denoted by

An n-dimensional enhanced hypercube Qn,kis obtained by adding some complementary edges from hypercube Qn,and it can be defined as follows:

Definition 1The enhanced hypercube Qn,k=(V,E)(1≤k≤n−1)is an undirected simple graph.It has the same vertices of Qn,that is,V={x1x2···xn:xi=0 or 1,1 ≤ i≤ n}.Two vertices x=x1x2···xnand y are connected by an edge of E if and only if y satisfies one of the following two conditions:

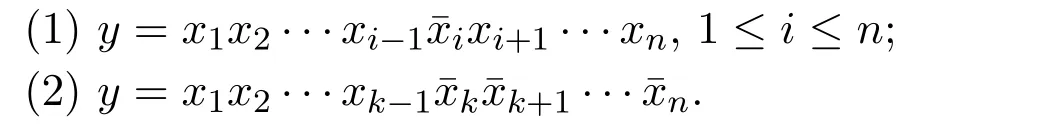
From Definition 1,the enhanced hypercubeis the extension of the hypercube Qnby adding the edgeswhich called complementary edges of enhanced hypercube,denoted bywhere u=x1x2···xn,andAs mentioned above,Qn,kcontains hypercube Qnas its subgraph.In addition,the folded hypercube FQn,which is the extension of the hypercube,is regarded as the special case of the enhanced hypercube when k=1.It has been showed that the enhanced hypercube Qn,kis(n+1)-regular,has 2n vertices and(n+1)2n−1edges,vertex-transitive and edge-transitive.Due to its good properties,the enhanced hypercube Qn,khave received substantial researches.

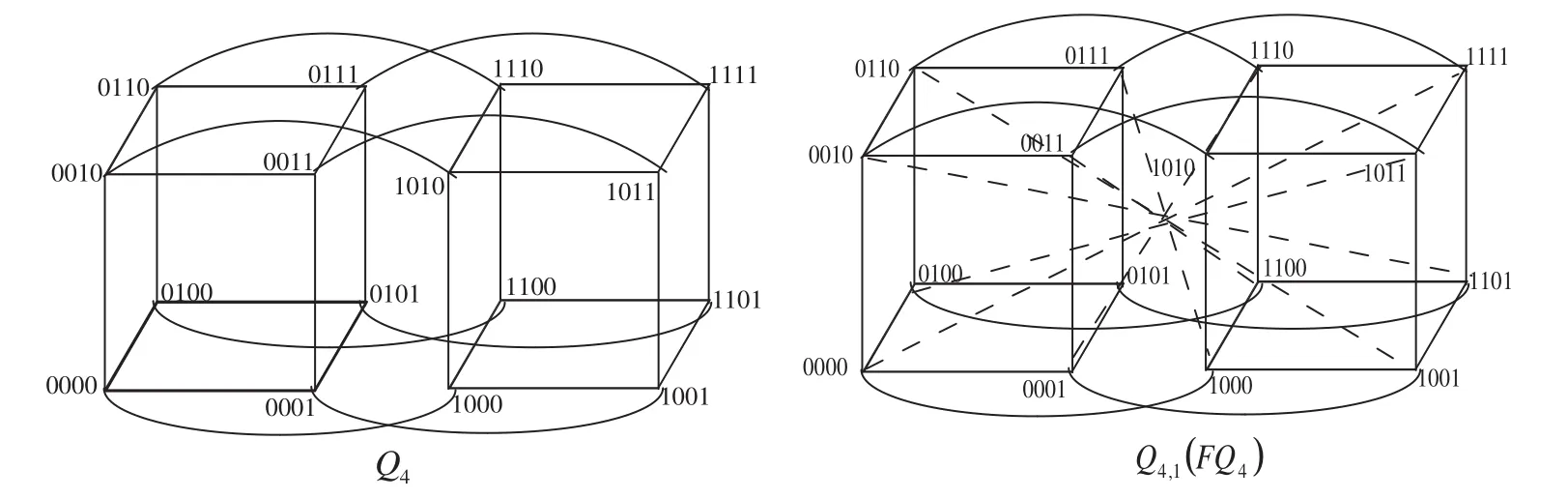
Figure 1:Q4,Q4,1(FQ4)(Dotted lines represent the complementary edges.)

Lemma 1[7]The enhanced hypercube Qn,kcan be partitioned into two subgraphs along some component i(1 ≤ i≤ n)such thatA vertex x1x2···xnbelongs toif and only if the ith position xi=0;similarly,x1x2···xnbelongs toif and only if the ith positionandare two(n − 1)-dimensional enhanced hypercubes;andare two(n−1)-dimensional hypercubes.

Guo made a good job in[14]and obtained thatfor n ≥ 2,for n ≥ 3.Next,We will propose a simple proof forfor n≥3.

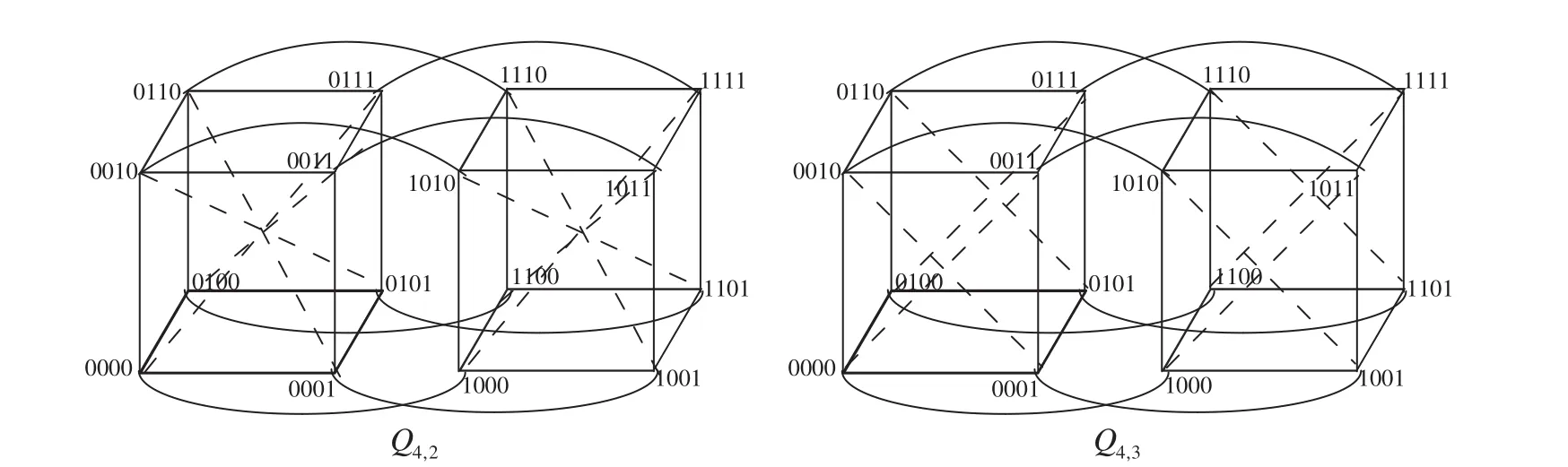
Figure 2:Q4,2,Q4,3(Dotted lines represent the complementary edges.)

Lemma 2[14](1)for n ≥ 2.(2)for n ≥ 3.

ProofSelect a 4-cycle C4,thenfor any vertex x ∈ C4,dC4(x)=2 and δ(Qn−C4)≥ 2,and Qn−C4is connected.ThereforeIn the following,we will proveby induction.

When n=3,it is easy to check that the conclusion is true.Suppose the conclusion is true for all positive integers less than n.We will consider the case of n≥4.

Let F ⊂E with|F|≤4n−9 such that each component of Qn−F has minimum degree greater than or equal to 2.We will prove Qn−F is connected.

Since n≥4,{(x,x1),(x2,x21),···,(xn,xn1)}⊂E1,there is{(x,x1),(x2,x21),···,that is,either(x,x1)is an edge joining x andor(2≤ i≤ n)is a required path connecting x and

The proof is complete.

3 Main Results

In this section,we demonstrate the conditional edge connectivity for enhanced hypercube networks.

Theorem 1

ProofSince the conditional edge connectivityis the cardinality of the minimum edge cut such that each component after removing the edge cut has minimum degree no less than k.This theorem means that there exists an edge cut F withsuch that Qn,k−F is disconnected and each component of Qn,k−F has minimum degree δ≥ 1.

If n=3,then k=2 or k=1.It is easy to checkandWe just consider n≥4.

Take a path P1of length one,that is an edge in Qn,k,thenis an edge cut ofwithand for any vertex x∈V(P1),The connectivity and the edge connectivity of Qn,kare n+1,that isis connected,thereforeThis leads to

On the other hand,the proof ofis needed.This will be proved by showing that for any edge subsetwithis connected.

According to Lemma 1,When i

Case 1Assume that there exists some dimension i ∈ {1,2,···,n}such thatIfthenforthenfor n>4.

No matter whatever cases occur,sinceandare connected.Furthermore there exists some vertexsuch that the edgeNoting thatis connected,hence

Case 2If there exists some dimension i∈ {k,k+1,···,n}such thatSince.Nowthenandare connected by Lemma 1.Sincefor n≥4.Then there exists some vertexjoined toby edgeor edgeThusis connected and

Case 3If there exists some dimension i∈ {k,k+1,···,n}such thatSinceWe have the following subcases:

Case 3.1If fL≤fR≤2n−5,the proof is similar to Case 2.

Case 3.2If fR=2n−4,thenis connected.For any vertex x∈whensaythe vertex x is joined toby the edge

Case 4If there exists some dimension i∈ {k,k+1,···,n}such thatSinceWe have the following subcases:

Case 4.1If fL≤fR≤2n−5,similar to Case 2,the the conclusion is true.

Case 4.2If fL≤1,fR≥2n−4,thenis connected.For any vertexwhen,saythe vertex x is joined toby the edge

Case 5If there exists some dimension i∈ {1,2,···,k−1}such that

Case 5.2.2If fL≤1,fR≥2n−4,thenis connected.For convenience,let i=1,thenFor any vertexwhenthe vertex x is joined toby the edge(x,x1).

When(x,x1)∈F,sincethere exists a j ∈ {2,3,···,n},say,Ifx can be connected toby the paththenNotingand the edgesare the same,ifthenWhenfR=2n−4;when fL=0,fR=2n−3,which implies that there exist some edgesHence eitheroris a path connecting x andThusis connected and

By analyzing the above cases,the proof of the theorem is complete.

And when the people saw it, there arose general laughter and derision,34 and she was so ashamed that she would rather have been a thousand fathoms33 below the ground

Theorem 2for 2 ≤ k ≤ n−1,n ≥ 3.

ProofIt is straightforward to prove the theorem when n=3 or 4.In the following,we just verify the conclusion n≥5 in Qn,k.

Select a 4-cycle C4in Qn,k,thenFor any vertexand for any vertexis connected.This leads to

On the other hand,we need to proveThis will be proved by consideringwithandis connected.

when i≥ k,Qn,kcan be partitioned into two(n−1)-dimensional hypercubesandalong some components i.In the following,letandthenFor convenience,suppose that fL≤fR.There are several cases needed to be considered according to the distribution of edges in F.

Case 1.1When i4.Since i≤k−1,for convenience,letting i=1,for any vertexwe will find a path joining x and

Case 1.1.2If the edge(x,x1) ∈ F,F.If|A|

Case 1.2When i≥k,Qn,kcan be partitioned into(n−1)-dimensional hypercubes along some components i,that isthenfor n≥4.Since i≥k,for convenience,let i=n,then for any vertexwe will find a path joining x and

Case 1.2.1If the edge(x,xn)ornot in F,the required path is(x,xn)orjoining x and

Case 2If there exists some dimension i∈ {1,2,···,n}such that fR≥ 4n − 8,thensois connected.We consider the following two subcases:

Case 2.1When i≥k,Qn,kcan be partitioned into two(n−1)-dimensional hypercubes along some components i,that isandthen.For any vertexif edgesthe conclusion is true.If edgessincefor any vertexwe can suppose edgeand(x,xt)∈/F.Becausesayso xxsxsiis the required path joining x and

Case 2.2When i

By analyzing the above cases,the proof of the theorem is complete.

4 Conclusion

Network topology is an important issue in the design of computer networks since it is crucial to many key properties such as the efficiency and fault tolerance.We consider the conditional edge connectivity for hypercube and enhanced hypercube networks.This parameter is the generalization of edge connectivity of graph,and can reflect the real cases more better.The results show that at least 2n edges must be removed to disconnect the n-dimensional enhanced hypercube networks,provided that the removal of these edges will preserve the each component having minimum degree one,and at least 4n−4 edges must be removed to disconnect the n-dimensional enhanced hypercube networks,provided that the removal of these edges will preserve the each component having minimum degree two.

This paper reveals the conditional edge connectivity of enhanced hypercube.The study of other conditional connectivity in the enhanced hypercube is one of our further projects.