SOME LIMIT PROPERTIES AND THE GENERALIZED AEP THEOREM FOR NONHOMOGENEOUS MARKOV CHAINS∗†

Ping Hu,Zhongzhi Wang

(School of Math.&Physics Science and Engineering,AnHui University of Technology,Ma’anshan 243002,Anhui,PR China)

Abstract Letbe a Markov chain with the state space X={1,2,···,b},be functions defined on X × X,and

Keywords AEP;nonhomogeneous Markov chains;limit theorem;generalized relative entropy density

1 Introduction

Throughout this paper,let the random variablesbe defined on a fixed probability space(Ω,F,P)taking on values in a finite set X={1,2,···,b}.Given two integers,we denote by ξm,nthe random vector of(ξm,···,ξn)and by xm,n=(xm,···,xn)a realization of ξm,n.Suppose the joint distribution of ξm,nis

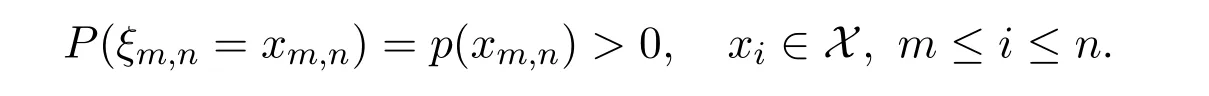
In what follows we shall assume thatis a fixed sequence of positive integers,is a sequence of integers satisfying:For every

Let

where log is the natural logarithm.The defined quantity ofis referred to as generalized relative entropy density of(see Wang and Yang[13]).Ifis a nonhomogeneous Markov chain with the state space X={1,2,···,b},the initial distribution

and the transition matrices

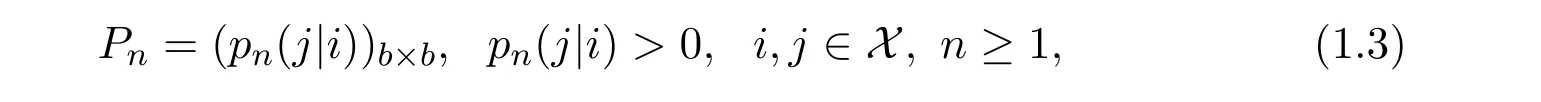
then

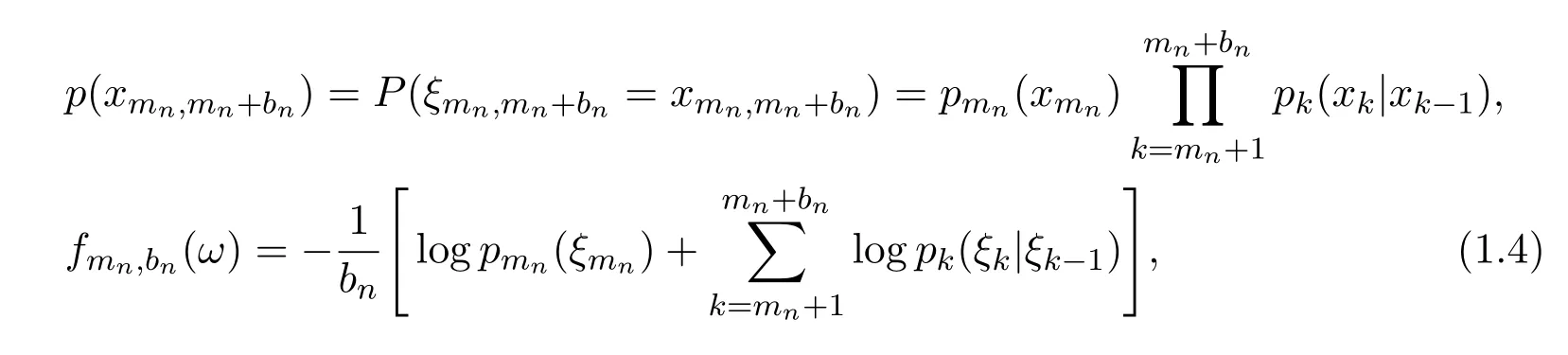
The statement of convergence of the relative entropy density f0,n(ω)to a constant limit called the entropy rate of the process is known as the ergodic theorem of information theory or asymptotic equipartition property(AEP).Shannon[11] first showed that for the stationary ergodic Markov chain f0,n(ω)converges in probability to a constant.McMillan[7]and Breiman[2]proved,respectively,that ifis stationary and ergodic,then f0,n(ω)converges inand almost everywhere to a constant.Since then,numerous extension have been made in many directions,such as weakening the hypothesis on the reference measure,state space,index set and required properties of the process.For example,in Feinstein[5],Chung[4],Moy[8],Kiefer[6],Perez[9]and Barron[1].

In the paper of Mark Schwartz[10],it is shown that ifandare two sequences of positive integers,and a measure-preserving ergodic transformation τ,the moving averagesconverge a.s..Motivated by the work of Schwartz,in this paper we first establish a class of limit theorems for finite nonhomogeneous Markov chains,then give an extend Shannon-McMillan(AEP)theorem.The conditions of our main theorems are slightly weaker than those of[13].

Theorem 1Let the Markov chainandandbe as in Theorem 7.Letbe the generalized relative entropy density ofdefined by(1.4).If

then

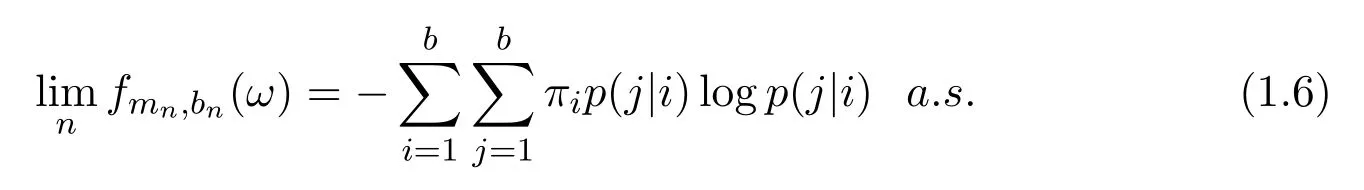
Remark 1Let mn=0,bn=n in(1.1),f0,n(ω)become the classical entropy density,then Theorem 9 in[12]is a special case of Theorem 1.In particular,if

then equation(1.6)also holds.

The rest of this paper is organized as follows:In Section 2,we prove some limit theorem for the delayed sum of the functions of two variables of finite nonhomogeneous Markov chains.In Section 3,we get some other limits for Markov chains and some limit theorems for the generalized relative entropy density,and finally,we give an extension of AEP theorem to the case of finite nonhomogeneous Markov chains.In the proof of our main results,the analytical technique put forward by Wang and Yang[13]is applied.

2 Preliminaries

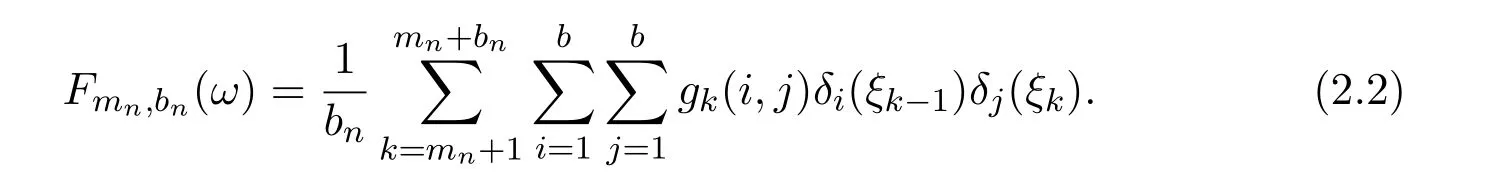
Lemma 1Ifis a sequence of positive random variables withc,for some constant c>0,then

ProofBy Markov inequality,for every ε>0,we have

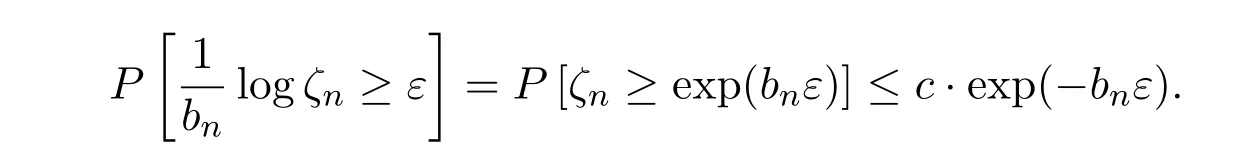
Hence

By the Borel-Cantelli lemma,taking a union over positive rational values of ε,with probability 1,The proof is completed.

The proof here is adapted from the proof of Theorem 2.1 in Wang and Yang[13].

Theorem 2Letbe a Markov chain defined by(1.2)and(1.3),be defined by(2.1),andbe as in Lemma 1.If there exists a constant α >0 satisfying that

then

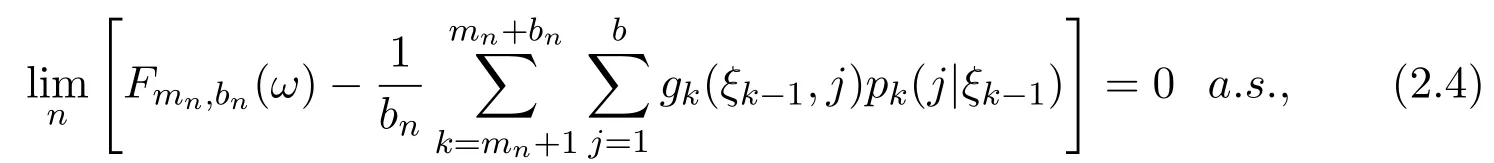
that is

ProofLetbe a constant.Define,for any i,j ∈ X,

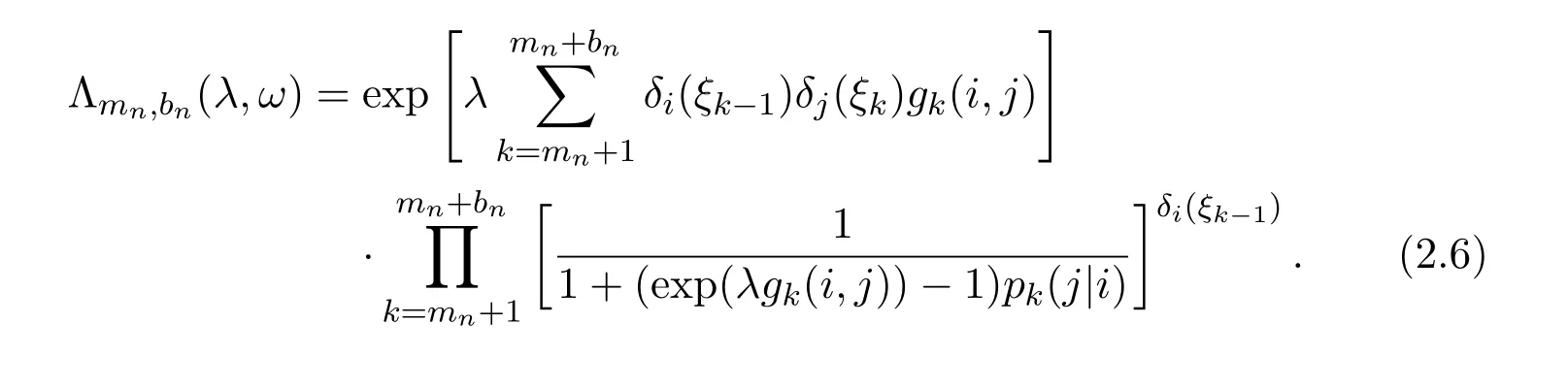
Note that

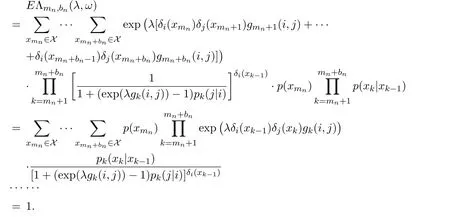
From equation(2.6),we have

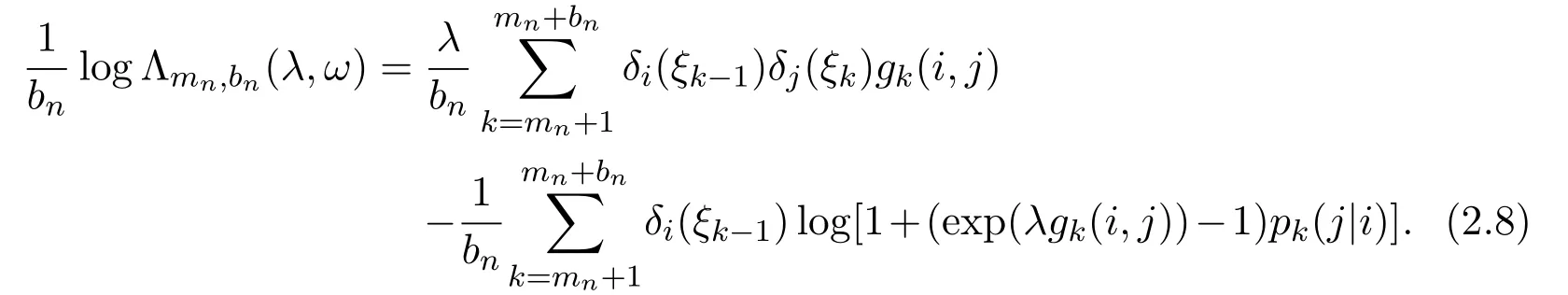
Equations(2.7)and(2.8)yield

(a)Putting λ >0,and dividing both sides of equation(2.9)by λ,we have

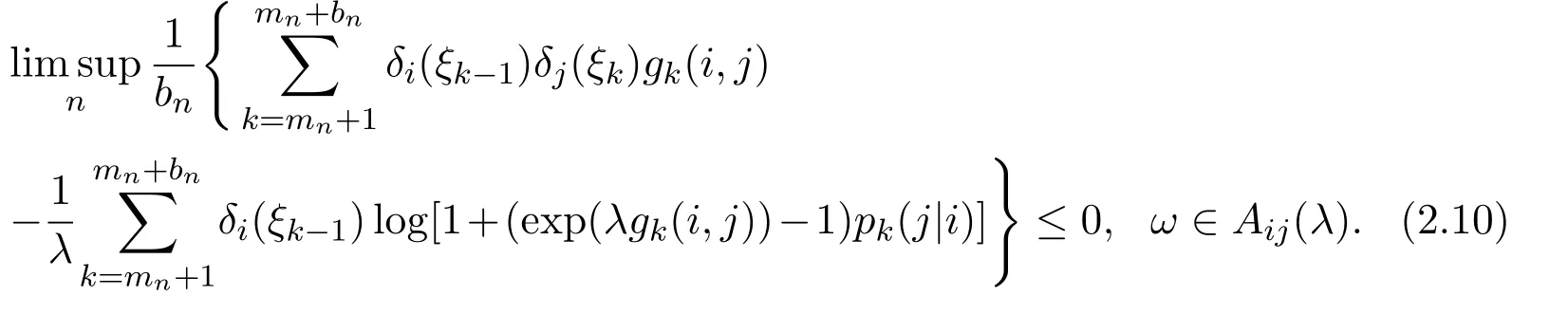
From equation(2.10)and the property of superior limit

and the facts log(1+x)≤x(x>−1)andwe obtain

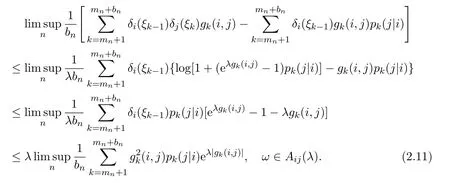
Choose λl∈ (0,α),l=1,2,···,such that λl→ 0 as l→ ∞,and denoteThen for all l≥ 1,we have by equations(2.11)and(2.3)

Since λl→ 0 as l→ ∞,we have by equation(2.12)that

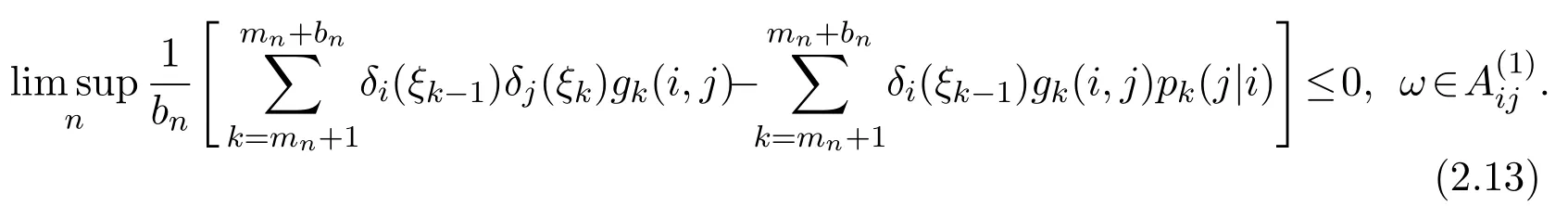
(b)Putting λ<0,an argument similar to the one used in(a)shows that there exists a setwithand

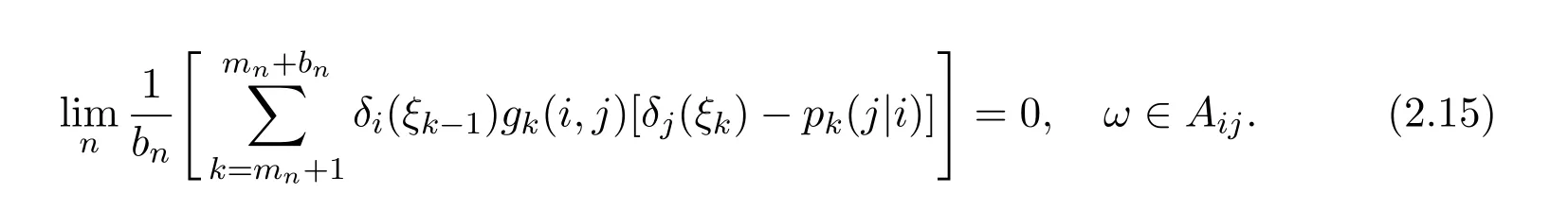
Since P(A)=1,equation(2.5)follows from equation(2.16)immediately.The proof is complete.

3 Some Limit Properties for Nonhomogeneous Markov Chains

Theorem 3Letbe Markov chain with the initial distribution(1.2)and the transition matrices(1.3),andbe the generalized relative entropy density defined as(1.4).Then

ProofPuttingin Theorem 1,we get

noticing that

By equations(3.2),(3.3),(1.4)and Theorem 1,equation(3.1)follows.The proof is completed.

Lemma 2Letbe a sequence of random variables taking value in X,g(·)andbe functions defined on X,and,be the number of i in the segment of,that is,

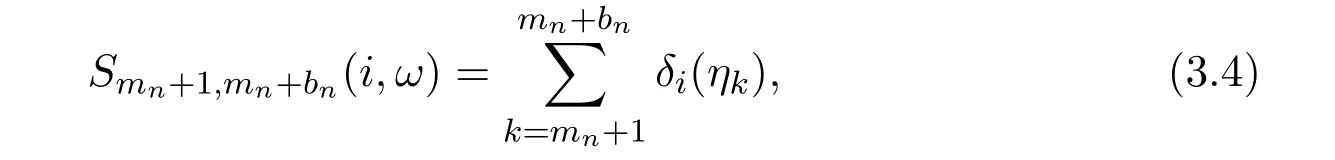
if

and the following limits exists

then

ProofApplying the triangle inequality|a−b|≤|a−c|+|c−b|,we have by equation(3.4)that

By equation(3.5),we get

By equation(3.6),we get

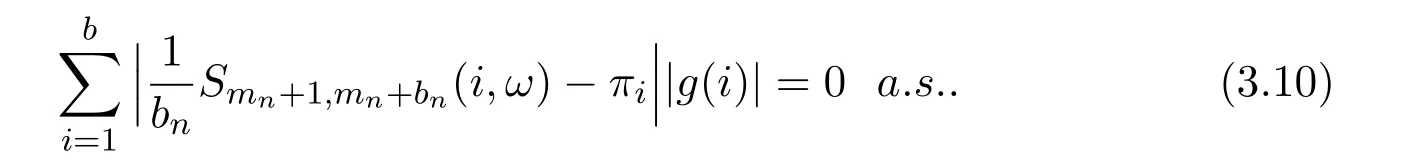
Then equation(3.7)follows immediately from equations(3.9)and(3.10).The proof is completed.

Theorem 4Let the Markov chainandbe as in Theorem 2,and g(x)be a function defined on X,andbe the number of i in the segmentthat is,

Assume that:

(a)There exists an α >0 such that equation(2.3)holds for all i,j ∈ X;

(b)

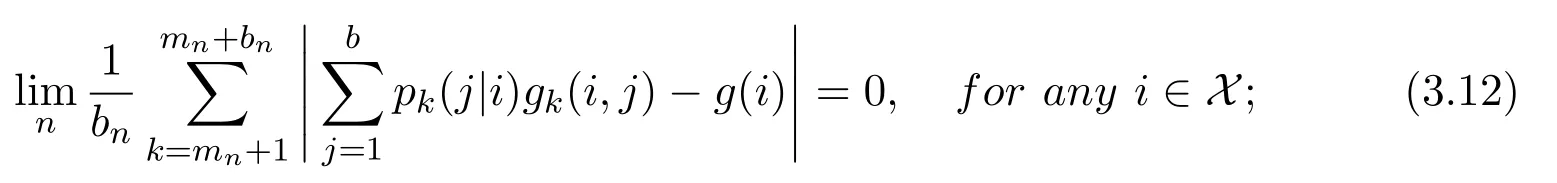
(c)the following limits exist

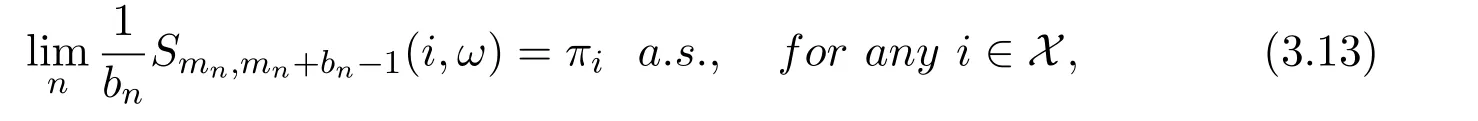
then

ProofPutin Lemma 1 and

We have by equations(3.12)and(3.13)that,

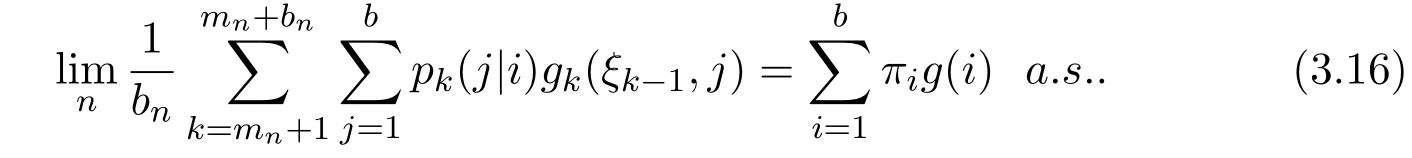
By(a)and Theorem 1,equation(2.4)holds.Then equation(3.14)follows from equations(3.15)and(3.16).The proof is completed.

Theorem 5Letandbe defined as in Theorem 4 andbe defined by(1.4).If

(a)

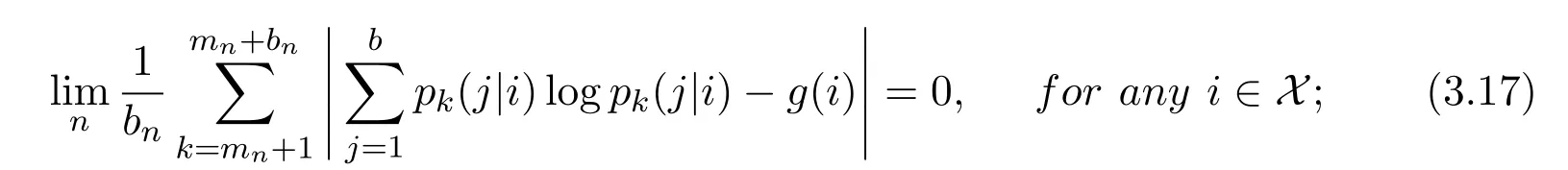
(b)the equality(3.13)holds for all i∈X.Then

ProofPuttingand

in Lemma 1,we have by equations(3.13)and(3.16)that

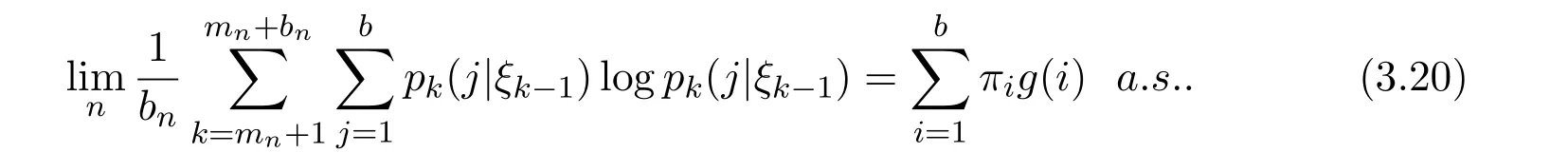
By Theorem 2,equation(3.1)holds.It is straightforward to show that equation(3.18)follows from equations(3.20)and(3.1).The proof is completed

Theorem 6Let the Markov chainandbe defined as in Theorem 4.Then

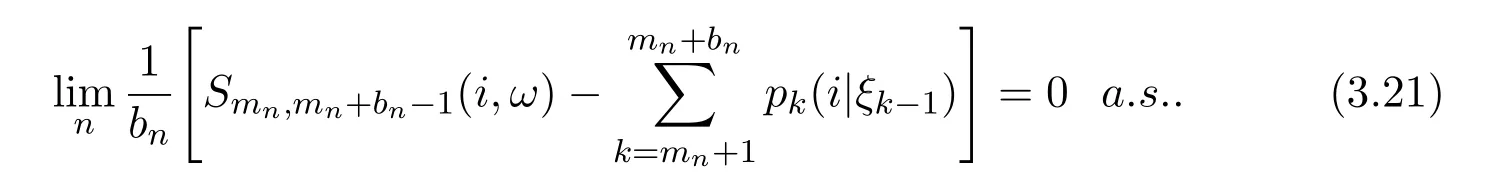
ProofPutting gk(x,y)= δi(y)(k ≥ 1)in Theorem 1,by equation(2.5)we have

By equation(3.22)and Theorem 2,equation(3.21)follows.The proof is completed.

Theorem 7Letbe a Markov chain defined as in Theorem 4,P=be an ergodic transition matrix,andbe the stationary distribution determined by P.For real number,denote

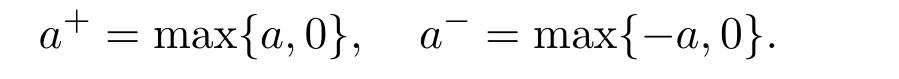
(a)For fixed j∈X,if

Then

(b)For fixed j∈X,if

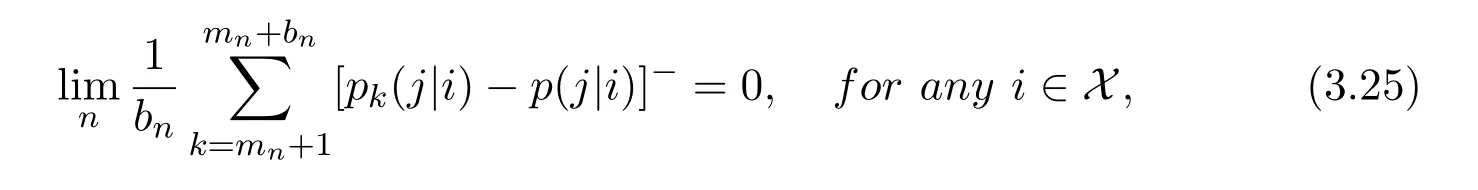
then

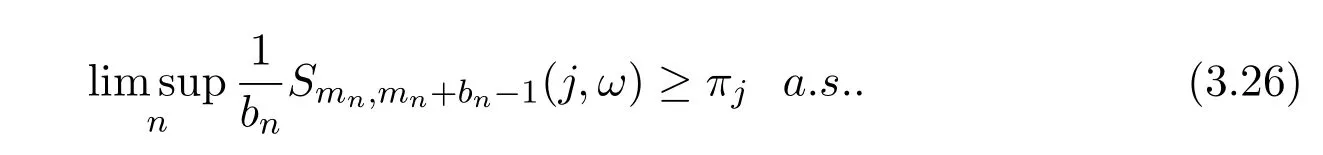
(c)For fixed j∈X,if

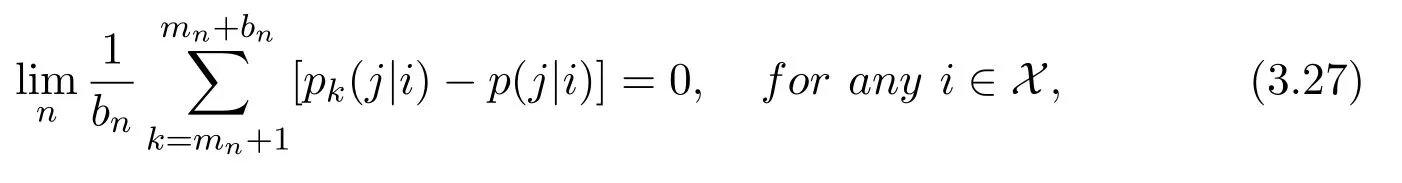
then

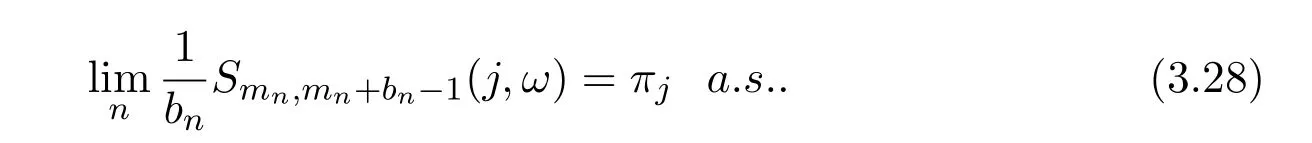
ProofWe have by equation(3.21)that

It is simple to show that,for the fixed j∈X,

Applying the properties of superior and inferior limits,we have by equations(3.24)and(3.30)that

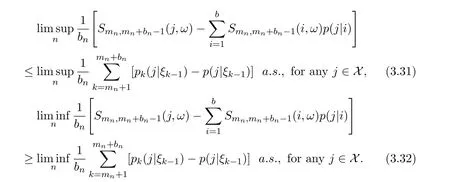
Obviously,

Multiplying both sides of equation(3.35)by p(k|j),and adding the obtained inequalities for j∈X,we have

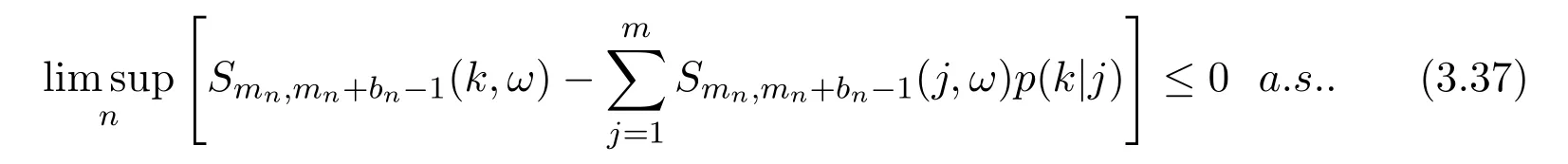
By equations(3.36)and(3.37),we obtain

By induction we have for all l≥1,

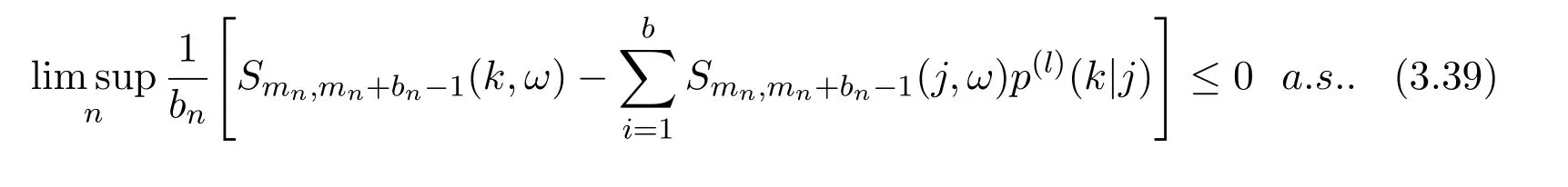
It follows that

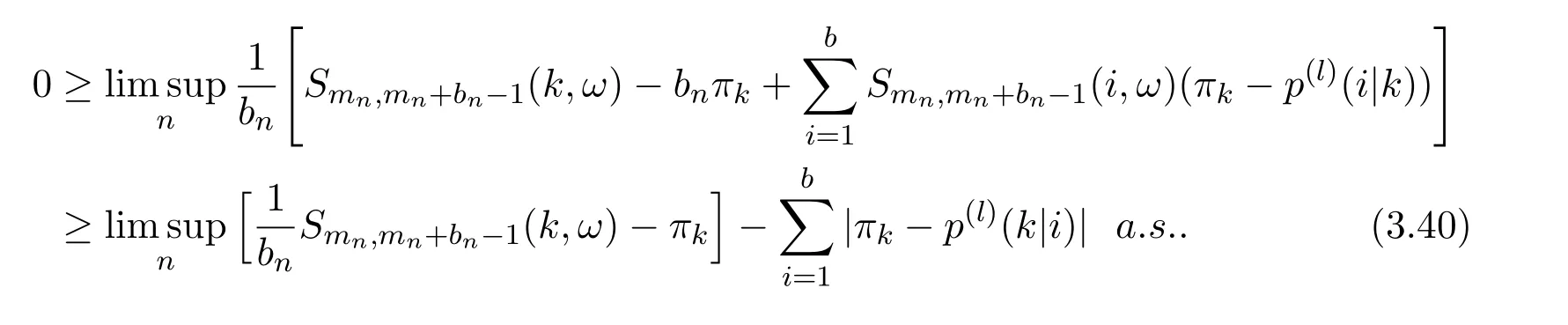
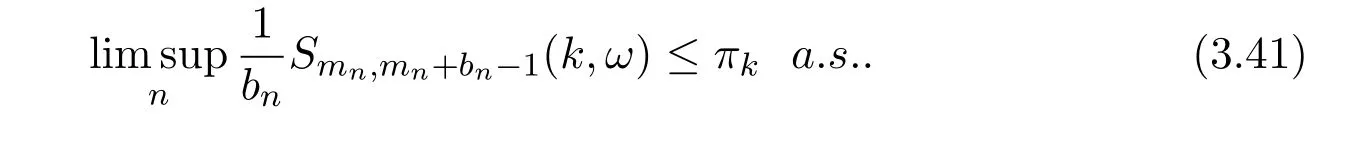
Hence,equation(3.24)follows.

(b)Suppose equation(3.25)holds,from(3.32)and(3.34),then we obtain

Thus,using arguments similar to those used to derive equation(3.39),we can show that

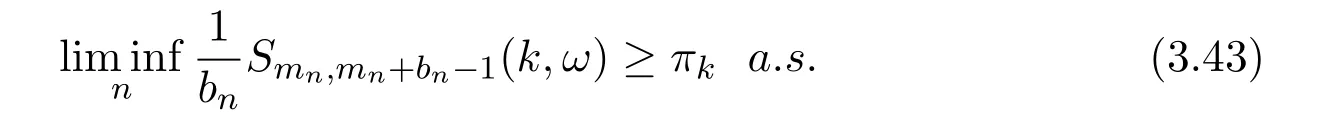
Hence,equation(3.26)follows.

(c)Suppose equation(3.27)holds.Obviously equations(3.23)and(3.25)follow from equation(3.27).

Therefore,equations(3.24)and(3.26)are true,and equation(3.28)follows.The proof is completed.

Theorem 8Letbe defined as in Theorem 7,and g(x)andbe functions defined on X.If equations(3.5)and(3.27)holds,then

ProofWe have by(c)of Theorem 7 that

Applying Lemma 1,equation(3.34)follows from equations(3.45)and(3.5).The proof is completed.

Lemma 3[3]Let f(x)be a bounded function defined on an interval I,andbe a sequence in I.If

and f(x)is continuous at point a,then

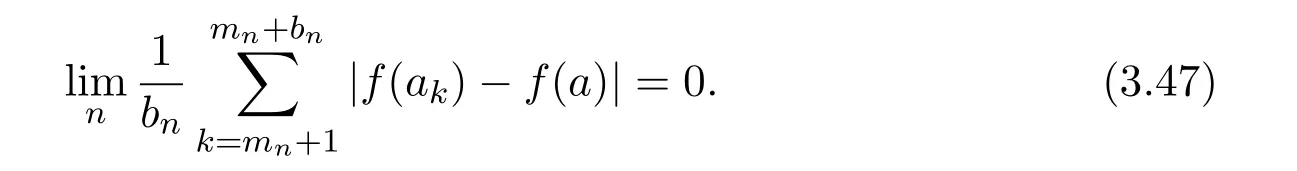
Theorem 9Letbe a Markov chain with the initial distribution(1.2)and the transition matrices(1.3),and g(x)be a continuous function defined on the interval(0,1]such that

Suppose that:

(a)There exists an α>0 such that

(b)

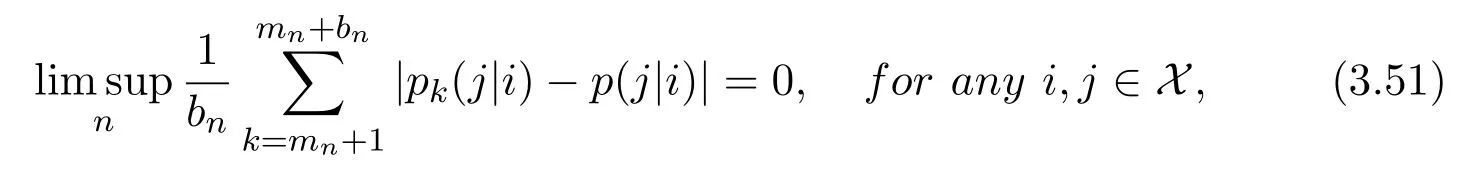
then

ProofLet

By equations(3.48)and(3.53),f(x)is continuous on[0,1],then from equation(3.51)and according to Lemma 2,we have

By equation(3.51)and Theorem 6,there is

Finally,we present the proof of Theorem 1.

Proof of Theorem 1Note that

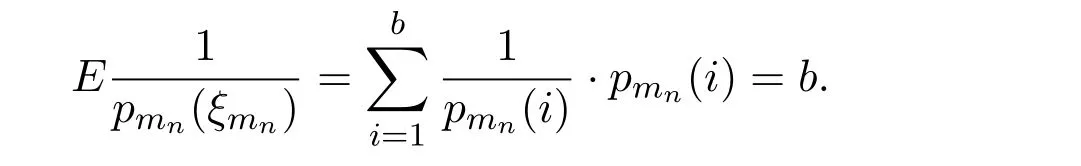
By Lemma 1,we have

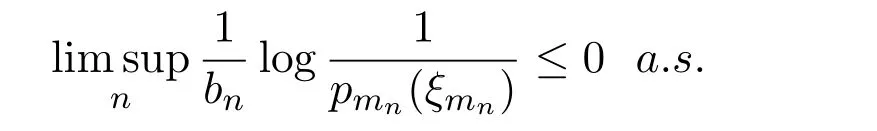
Notice that

By the condition(1.5),we have

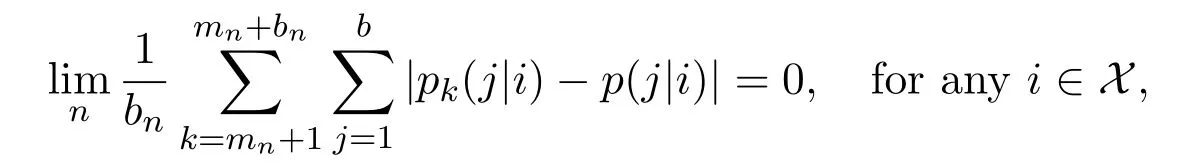
which implies

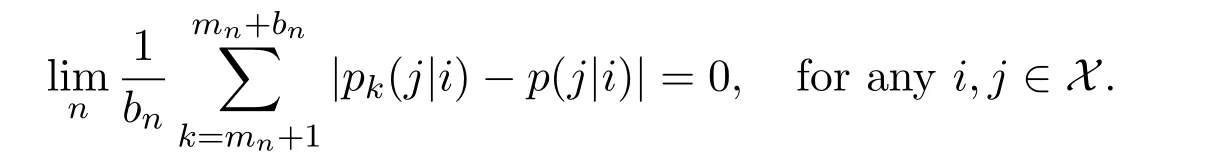
By this together with the inequalitywe have

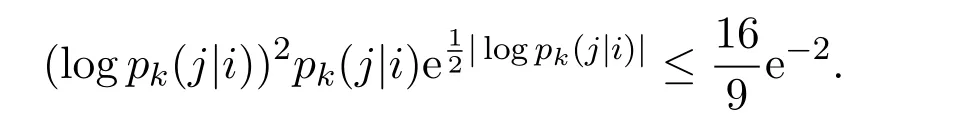
Putting g(x)=logx in Theorem 8,it is easy to verify that equation(3.50)holds(see Theorem 2 and equation(3.3)).

Thus equation(1.6)follows from(1.4),(3.56)and Theorem 8.The proof is completed.

AcknowledgmentThe authors would like to thank the anonymous reviewers for their suggestions to improve the presentation.