THREE KIRCHHOFFIAN INDICES OF THE CACTUS GRAPHS∗†

Ailian Chen,Minyin Yang

(College of Math.and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)

Abstract In this paper we give six explicit formulae to compute the Kirchho ffindex,the multiplicative degree-Kirchho ffindex and the additive degree-Kirchhoffindex of the k-cactus chain and the cactus graph which can be obtained from a k-cactus chain by expanding each of the cut-vertices to a cut edge.

Keywords polyphenyl chain;cactus graph;Kirchho ffindex;multiplicative degree-Kirchho ffindex;additive degree-Kirchho ffindex

1 Introduction

The objects nowadays known as cactus appeared in the scientific literature more than half a century ago.Motivated by papers of Husimi[28]and Riddell[41],[44]dealt with cluster integrals in the theory of condensation in statistical mechanics.Besides statistical mechanics,where cacti and their generalizations serve as simplified models of real lattices[36,42],the concept has also found applications in the theory of electrical and communication networks[56]and in chemistry[25,55].Many topological indices have been studied for these structures,including the matching and independence polynomials[4,16],the Hosoya indices[1],π-electron energy[52],the Hosoya polynomials[32],and the subtree numbers[50].

A cactus graph G is a connected graph in which each edge lies on at most one cycle.Therefore,each block in G is either an edge or a cycle.A k-cactus is a cactus in which each block is a k-cycle.A k-cactus chain is a k-cactus in which each block contains at most two cut-vertices and each cut-vertex lies in exactly two blocks.The number of blocks in a k-cactus chain is the length of the chain.A 6-cactus chain is also called spiro hexagonal chain,and a polyphenyl chain is a cactus graph which can be obtained from a 6-cactus chain by expanding each of the cut-vertices to an cut edge.For example,see the first graph in Figure 1.

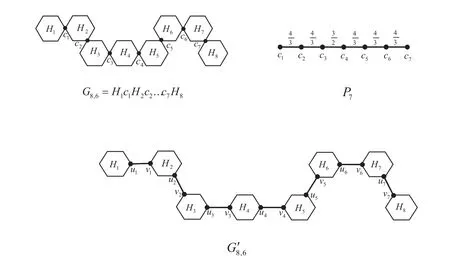
Figure 1:A spiro hexagonal chain,its corresponding weighted path and polyphenyl chain

Let G be a connected graph.The vertex set and edge set of G are denoted by V(G)and E(G),respectively.Based on the theory of electrical networks,Klein and Randić[30]introduced a new distance function named resistance distance.The resistance distance between a pair of vertices u and v in G,denoted by rG(u,v)or r(u,v),is the effective resistance between them in the electrical network N constructed from G by replacing each edge with a unit resistor.This new intrinsic graph metric has being recognized as having more nice purely mathematical,chemical and physical interpretations[7,12,29–31].

Analogous to distance-based graph invariants,various graph invariants based on resistance distance have been defined and studied.Among these invariants,the most famous one is the Kirchho ffindex[30],also known as the total effective resistance[21]or the effective graph resistance[18].Like many topological indices,the Kirchho ffindex is a structure descriptor and has been found very useful in purely mathematical,physical and chemical interpretations[30,31,54].If the ordinary distance is replaced by the resistance distance in the expression for the Wiener index[47],one arrives at the Kirchho ffindex[30].

Definition 1.1The Kirchho ffindex of a graph G is denoted by Kf(G)and defined as follows:

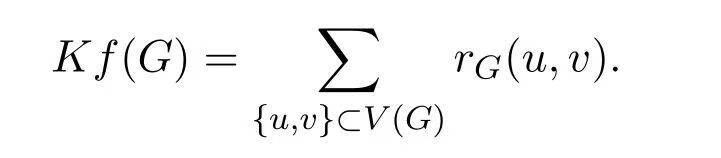
Recently,two modifications of the Kirchho ffindex,which takes the degrees of the graph into account,have been considered.One is the multiplicative degree-Kirchhoffindex introduced by Chen and Zhang[11].If the ordinary distance is replaced by resistance distance in the expression for the Gutman index[22],then one arrives at the multiplicative degree-Kirchho ffindex.

Definition 1.2The multiplicative degree-Kirchho ffindex of a graph G is denoted by Kf∗(G)and defined as follows:

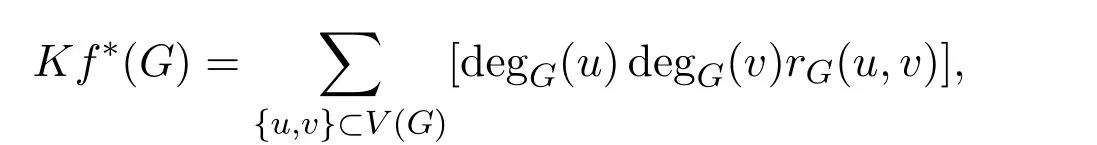
where degG(u)is the degree of u in G.

The other one is the degree resistance distance introduced by Gutman et al.[24].If the ordinary distance is replaced by resistance distance in the expression for the degree distance[15,22],then one arrives at the degree resistance distance.

Definition 1.3The degree resistance distance of a graph G is denoted by Kf+(G)and defined as follows:

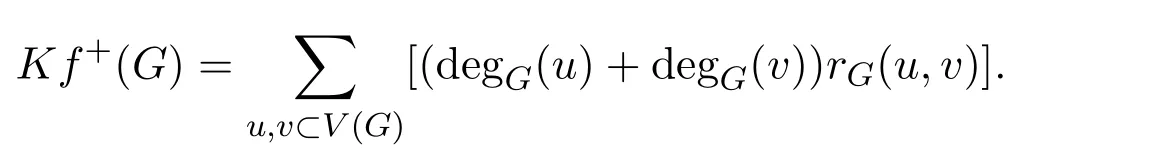
Palacios[38]named the same graph invariant“additive degree-Kirchho ffindex”.

The three Kirchhoffian indices have received much attention in recent years.Much work has been done to compute the three indices of some classes of graphs,or give some bounds for the three indices of graphs and characterize extremal graphs.In particular,Yang and Klein[49]gave formulae for the three indices of iterated subdivisions and triangulations of graphs.Huang et al.[27]gave some relations among the three indices of a connected graph and extended some results in[49].In[17,34],the authors determined the first three minimum additive degree-Kirchhoffindices among all the cacti possessing fixed number of the vertices and cycles and characterized the corresponding extremal graphs.Deng et al.[14]obtained the explicit formulae to compute the Kirchho ffindices of spiro and polyphenyl hexagonal chains,determined the extremal values and characterized the extremal graph with respect to the Kirchho ffindex among all spiro and polyphenyl hexagonal chains with h hexagons.Palacios[40]reviewed some known facts of the three indices,and found new relations among them.Motivated by the above results,in this paper we study the three Kirchhoffian indices of the k-cactus chain.

In this paper we obtain six explicit formulae to compute the Kirchho ffindex,the multiplicative degree-Kirchho ffindex and the additive degree-Kirchho ffindex of the k-cactus chain and the cactus graph which can be obtained from a k-cactus chain by expanding each of the cut-vertices to a cut edge.Our results extend the main results in[14].Moreover it reduces the problems on the three Kirchhoffian indices of the the graphs in the above two classes to the Winer index of the weighted-path,which make it trivial to determine the extremal problems on the three indices of the cactus graphs in the above two classes.The rest of the paper is organized as follows.We present our results in Section 2 and their proofs in Section 3.

2 Main Results

It is not difficult to see that beginning from a Ck,a k-cactus chain can be obtained by stepwise additions of a new terminal Ck.Denote bya k-cactus chain with h k-cycles,where Hiis the ith k-cycle of Gh,kand ciis the common cut vertex of Hiand Hi+1,i=1,2,···,h − 1.Denote bythe corresponding cactus graph obtained by expanding each of the cut-vertices ciof Gh,kto a cut edge(ui,vi)with ui∈Hiand vi∈Hi+1.For an example see Figure 1.Obviously,Gh,kis determined completely by its cut vertex sequence c1,c2,···,ch−1.

Recall that for an edge-weighted graph(G,ω),the length of a path in(G,ω)is the sum of the weights of all the edges in the path and the distance between u and v,and denote by dG(u,v)the minimum length of all the(u,v)-path.The Wiener index of an edge-weighted graph(G,ω)is defined as

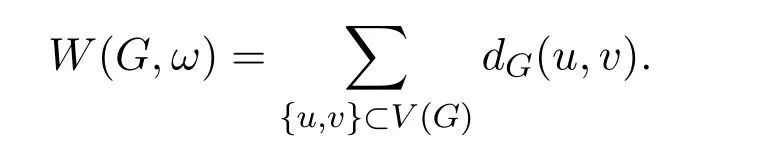
Therefore,for a k-cactus chain

Theorem 2.1Let Gh,kbe a k-cactus chain with h k-cycles,be the corresponding cactus graph obtained by expanding each of the cut-vertices ciof Gh,kto a cut edge and(Ph−1,ωr)be the corresponding edge-weighted path.Then

(1)

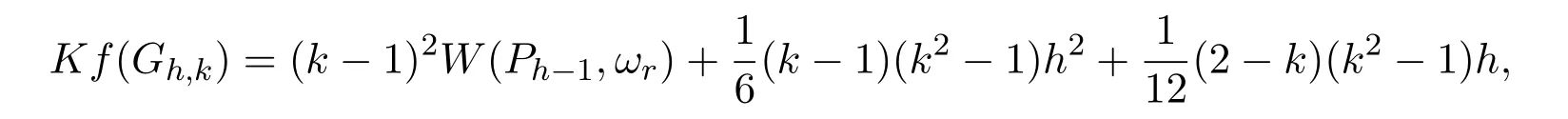
(2)

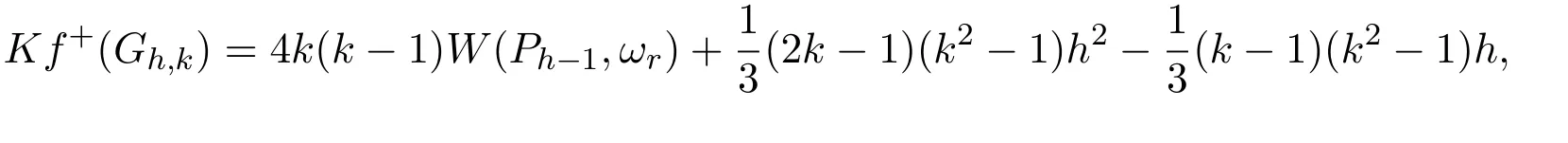
(3)

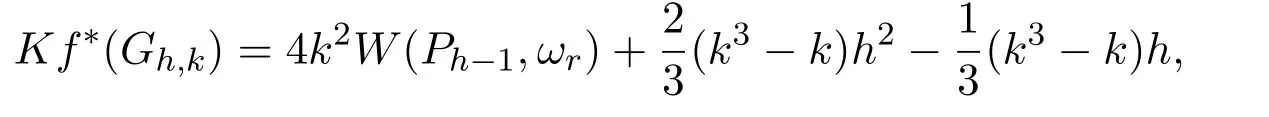
(4)

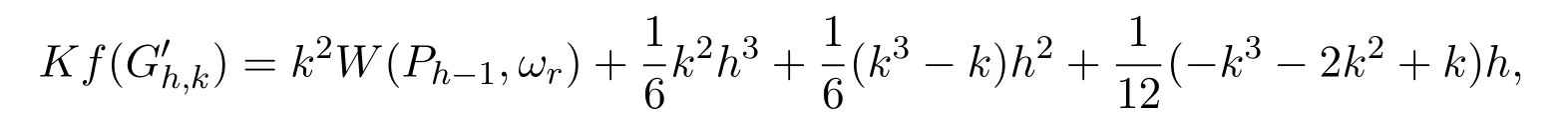
(5)

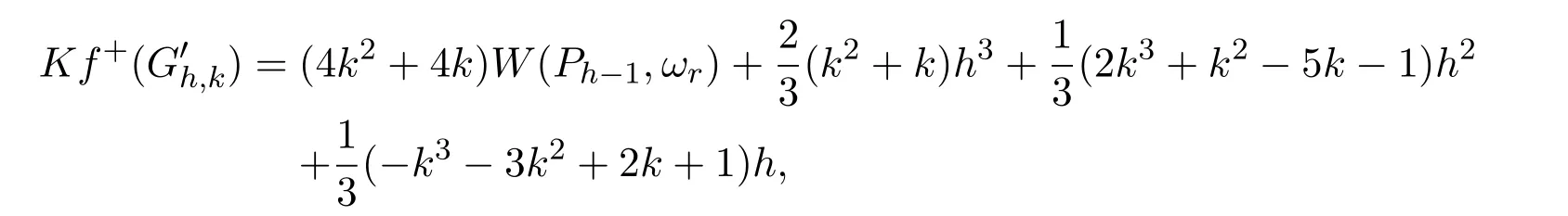
(6)

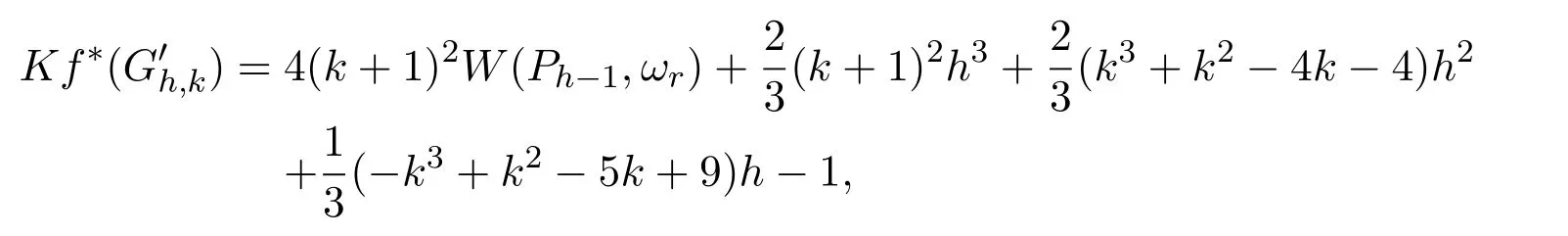
which imply that

(7)

(8)

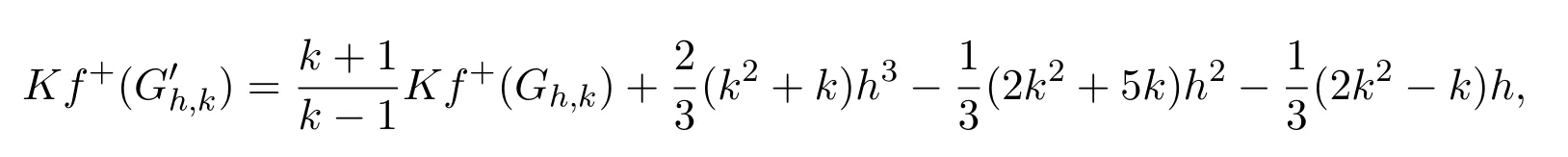
(9)

Let k=6.Then we have the following corollary.

Corollary 2.1Suppose that PPChis a polyphenyl chain with h(h≥2)hexagons,SPChis the corresponding 6-cactus chain obtained from PPChby squeezing o ffits cut edges and(Ph−1,ωr)is the corresponding edge-weighted path to SPCh.Then

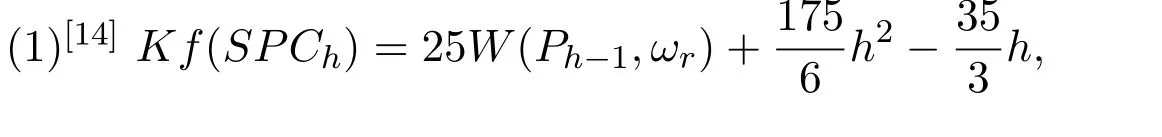
Our main results reduce the problems on the Kirchho ffindex(or multiplicative degree-Kirchho ffindex,additive degree-Kirchho ffindex)of the k-cactus chain and the corresponding cactus graph,which can be obtained from a k-cactus graph by expanding each of the cut-vertices to a cut edge to the corresponding problems on the Wiener index of the weighted path,in which the weight of each edge is in the set

For example,if k=6,then extremal problems on the polyphenyl and spiro chains with h hexagons are determined on the extremal problems on the Wiener of the weighted path Ph−1,in which the weight of each edge is

Corollary 2.2Supposeto be a k-cactus chain with h k-cycles.Then the Kirchho ffindex(or multiplicative degree-Kirchho ffindex,additive degree-Kirchho ffindex)of Gh,kreceives the maximum value when

and the minimum value when

Remark 2.1From the proof of Theorem 2.1,it can be found that,the above results also hold if we replace“Gh,ka cactus chain”by “Gh,kis a k-cactus graph,in which any cut vertex is at most in two k-cycles”.

3 The Proof of Main Result

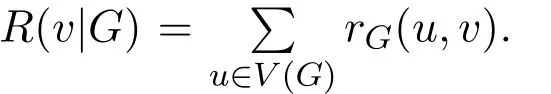
Lemma 3.1[24]Let Ckbe the cycle with k vertices,and v∈V(Ck).Then

Lemma 3.2[46]Suppose that G1and G2are two connected graphs withniandIf we identify any vertex,say x1,of G1with any other vertex,say x2,of G2as a new common vertex x,and obtain a new graph G,then

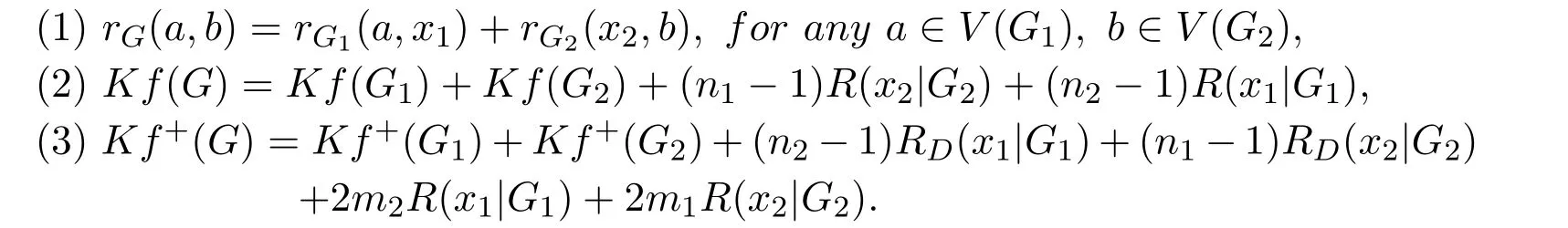
Lemma 3.3Suppose that G1and G2are two connected graphs withni,andIf we identify any vertex,say x1,of G1with any other vertex,say x2,of G2as a new common vertex x,and obtain a new graph G,then

ProofBy the definition of the multiplicative degree-Kirchho ffindex of a graph G,we have

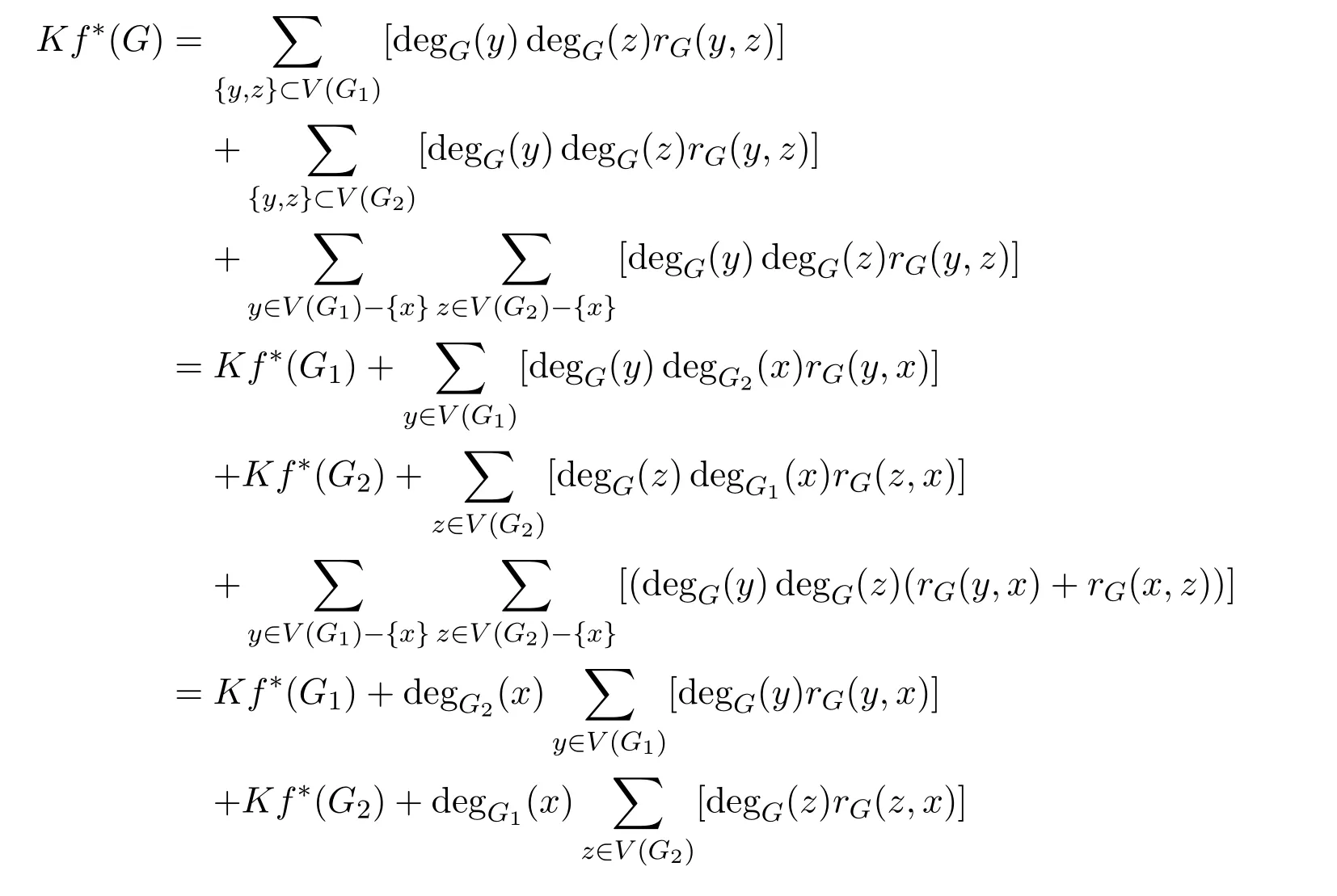
The proof is completed.

Lemma 3.4Let e=(x1,x2)be a cut edge of G.Suppose that G1and G2are two connected components of G−e with(i=1,2).Then

ProofBy the definition of the Kirchho ffindex and Lemma 3.2,we have

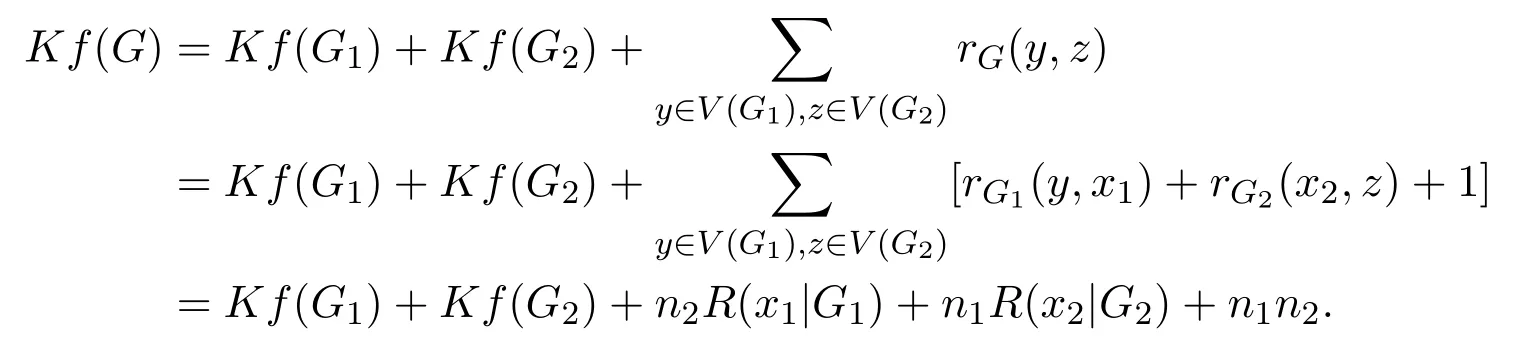
Similarly,

The proof is completed.

Lemma 3.5Letbe a k-cactus chain with h kcycles andbe the corresponding cactus graph obtained by expanding each of the cut-vertices ciof Gh,kto a cut edge(ui,vi)with ui∈Hiand vi∈Hi+1,as showed in Figure 1.Denote bythe corresponding subgraph of Gh,k.Then

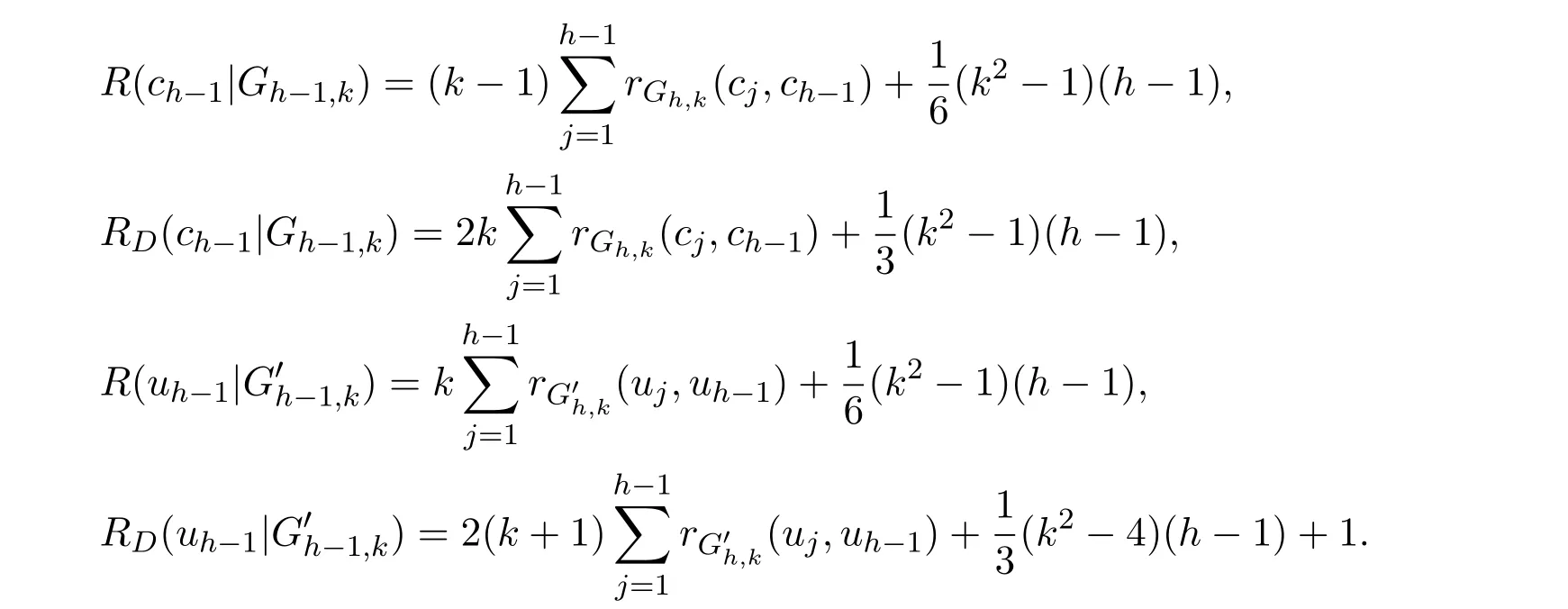
ProofBy Lemma 3.1which implies that in Gh,kthe sum of the resistance distances between ch−1and all the vertices inis

Then

Similarly,

The proof is completed.

Proof of Theorem 2.1SupposeDefine bythe corresponding subgraphs of Gh,k.Obviously,

Then by Lemma 3.2,

By the same way

It is not difficult to see thatSo

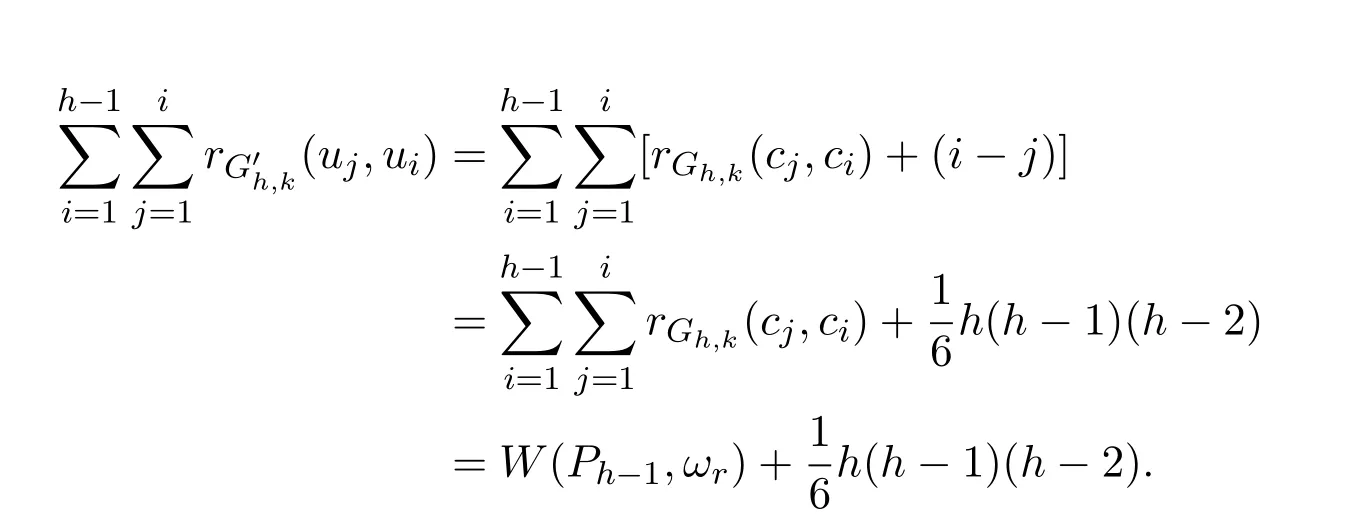
Then

Similarly,by Lemmas 3.4 and 3.5

The proof is completed.