EXISTENCE OF PERIODIC SOLUTION FOR A KIND OF THIRD-ORDER GENERALIZED NEUTRAL FUNCTIONAL DIFFERENTIAL EQUATION WITH VARIABLE PARAMETER∗

A.M.Mahmoud

(Dept.of Math.,Faculty of Science,New Valley Branch,Assiut University,New Valley,El-Khargah 72111,Egypt)

E.S.Farghaly

(Dept.of Math.,Faculty of Science,Assiut University,Assiut 71516,Egypt)

Abstract In this paper,we investigate a third-order generalized neutral functional differential equation with variable parameter.Based on Mawhin’s coincidence degree theory and some analysis skills,we obtain sufficient conditions for the existence of periodic solution for the equation.An example is also provided.

Keywords existence of periodic solution;third-order neutral functional differential equation;variable parameter;Mawhin’s continuation theorem;coincidence degree

1 Introduction

Neutral differential equations are widely used in many fields including biology,chemistry,physics,medicine,population dynamics,mechanics,economics,and so on(see[6,8,10,27]).For example,in population dynamics,since a growing population consumes more(or less)food than a matured one,depending on individual species,this leads to neutral equations[10].These equations also arise in classical cobweb models in economics where current demand depends on price,but supply depends on the previous periodic[6].In recent years,the problem of the existence of periodic solutions for neutral differential equations has been extensively studied in the literature.We refer the reader to[1-5,11-14,17-19,21-24]and the references cited therein for more details.

In this paper,we consider the generalized neutral functional differential equation with variable parameter

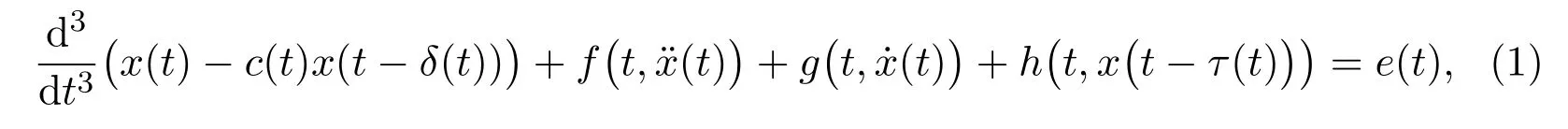
In recent years,when c(t)is a constant c or δ(t)is a constant δ or both of them are constants,many researchers have extensively studied such types of neutral functional differential equations.We refer the reader[9,15-17,20,26]and their references therein.But the work to study the existence of periodic solutions for neutral functional differential equations with variable parameter has rarely appeared.There are two reasons for this.The first reason is that the criterion of L-compact of nonlinear operator N on the setis difficult to establish when c(t)is not a constant.The second reason is that the linear operatorfor all t∈[0,T],has continuous inverse A−1,which is far away from the answer.

For example,Du et al.[5]investigated the second-order neutral equation

by using Mawhin’s continuous theorem,the authors obtained the existence of periodic solution for(2).

Afterwards,in[19],Ren et al.considered the following neutral differential equation with deviating arguments:

by the continuation theorem and some analysis techniques,some new results on the existence of periodic solutions were obtained.

Recently,Xin and Zhao[25]studied the neutral equation with variable delay

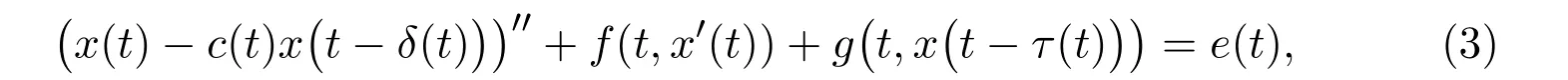
by coincidence degree theory and some analysis skills,the authors obtained sufficient conditions for the existence of periodic solution for(3).

Motivated by[5,19,25],in this paper,we consider the generalized neutral equation(1).Notice that here the neutral operator A is a natural generalization of the familiar operatorBut A possesses a more complicated nonlinearity than Ai,i=1,2,3.For example,the neutral operator A1is homogeneous in the following sensewhereas the neutral operator A in general is inhomogeneous.As a consequence,many of the new results for differential equations with the neutral operator A will not be a direct extension of known theorems for neutral differential equations.

The paper is organized as follows.In Section 2,we first analyze qualitative properties of the generalized neutral operator A,which will be helpful for further studies of differential equations with this neutral operator;in Section 3,by Mawhin’s continuation theorem,we obtain the existence of periodic solution for the generalized neutral equation with variable parameter.An illustrative example is given in Section 4.

2 Analysis of the Generalized Neutral Operator with Variable Parameter

Let

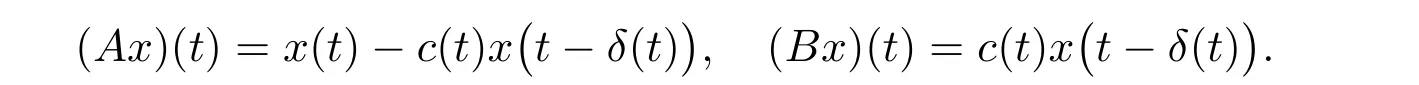
Lemma 2.1[25]If,then the operator A has a continuous inverse A−1on Cωsatisfying

(1)

(2)

(3)

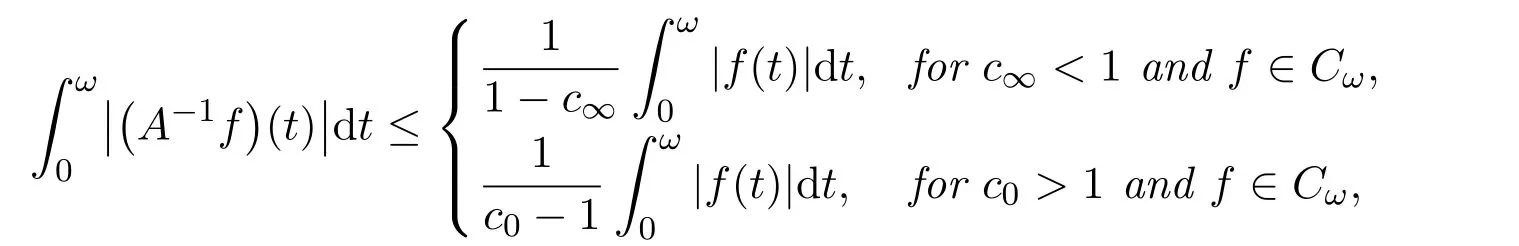
3 Existence of Periodic Solution for(1)

We first recall Mawhin’s continuation theorem,which our study is based upon.Let X and Y be real Banach spaces andbe a Fredholm operator with index zero,here D(L)denotes the domain of L.This means that ImL is closed in Y and dimKerConsider supplementary subspaces X1,Y1,of X,Y,respectively such thatLetanddenote the natural projections.Clearly,Kerthus the restrictionis invertible.Letdenote the inverse of LP1.

Let Ω be an open bounded subset of X with.A mapis said to be L-compact inifis bounded and the operatoris compact.

Lemma 3.1[7]Suppose that X and Y are two Banach spaces,and L:D(L)⊂X→Y is a Fredholm operator with index zero.Furthermore,Ω⊂X is an open bounded set andis L-compact onAssume that the following conditions hold:

In order to use Mawhin’s continuation theorem to study the existence of ωperiodic solutions for(1),we rewrite(1)in the following form:

by

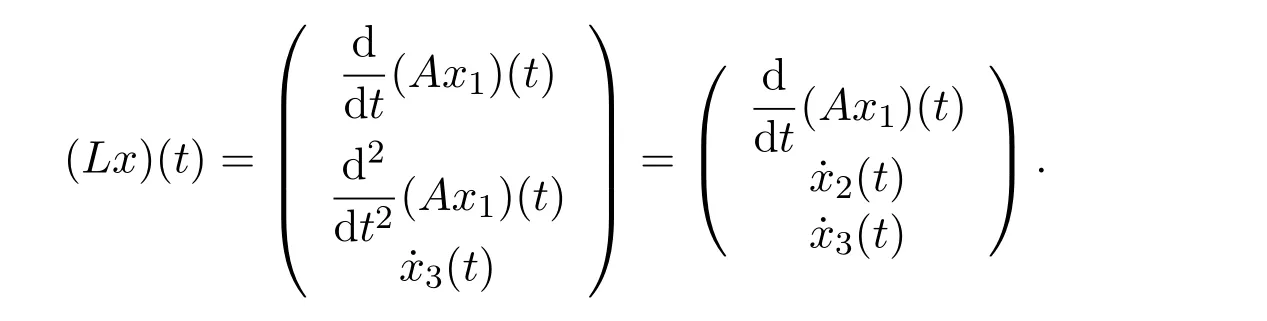
Also define N:X→Y by

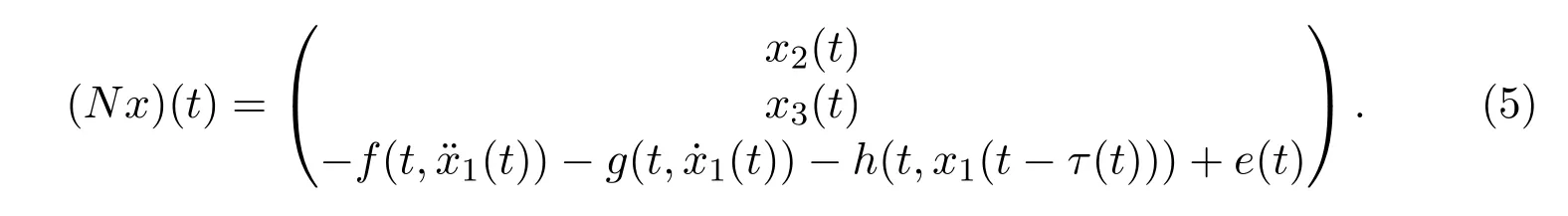
Then(4)can be converted to the abstract equation Lx=Nx.From the definition of L,one can easily see that

So L is a Fredholm operator with index zero.Let P1:X→KerL and Q1:Y→ImQ1⊂R3be defined by

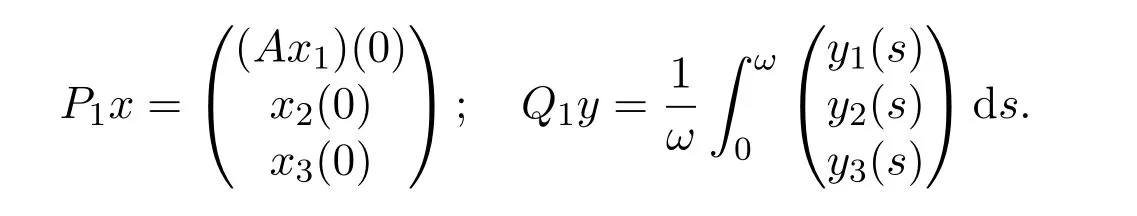
Then ImP1=KerL,KerQ1=ImL.Setand let:ImL →D(L)denote the inverse of LP1,then it follows that

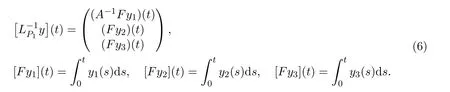
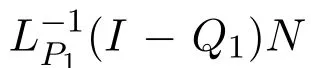
(H1)There exists a positive constant K1such that|f(t,u)|≤K1for(t,u)∈R×R;

(H2)there exists a positive constant K2such that|g(t,u)|≤K2for(t,u)∈R×R;

(H3)there exists a positive constant D such that|h(t,x)|>K1+K2and x[f(t,u)+for t,u,v,x ∈ R and|x|>D;

(H4)there exists a positive constant mosuch thatfor all t,x1,x2∈R.

Now we give our main results on periodic solutions for(1).

Theorem 3.1Assume that conditions(H1)-(H4)hold.Suppose that one of the following conditions is satisfied:

(i)If c∞<1 and 1− c∞− c∞δ1(δ1− 2)− M6>0;

(ii)if c0>1 and c0−1−c∞δ1(δ1−2)−M6>0,

where

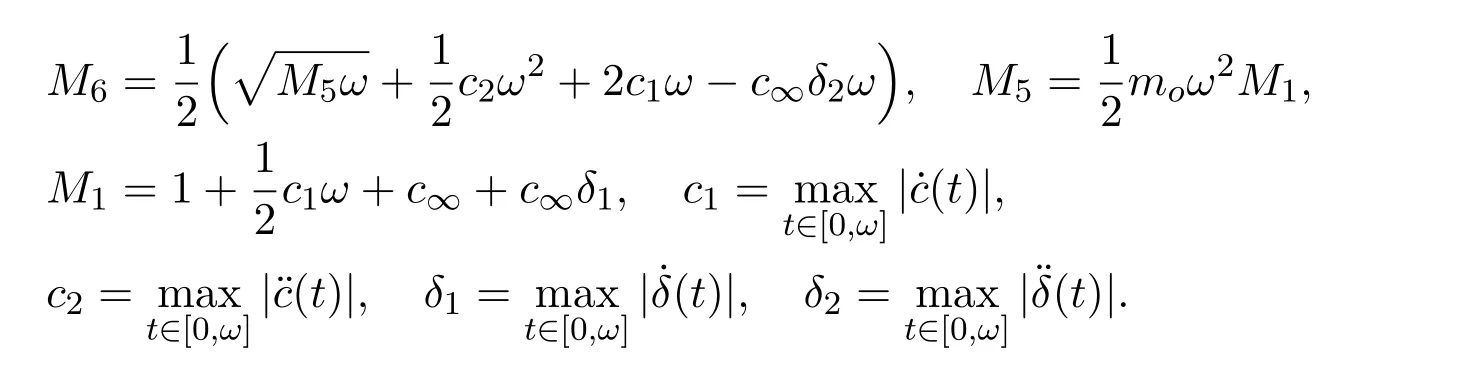
Then equation(1)has at least one ω-periodic solution.

ProofBy construction,(4)has an ω-periodic solution,if and only if,the following operator equation

has an ω-periodic solution.From(5)we see that N is L-compact onwhere Ω is any open,bounded subset of Cω.For λ ∈ (0,1],define Ω1={x ∈ Cω:Lx= λNx}.Thensatisfies

Therefore we find

Integrating both sides of(8)over[0,ω],we have

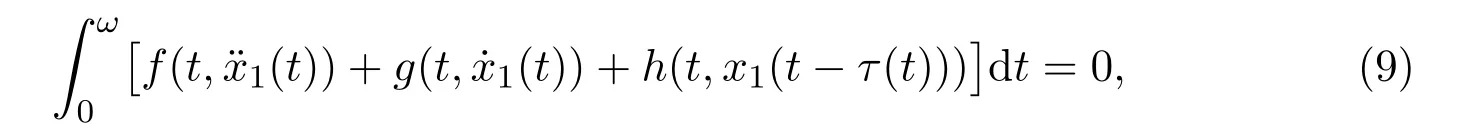
which yields that there exists at least one point t1such that

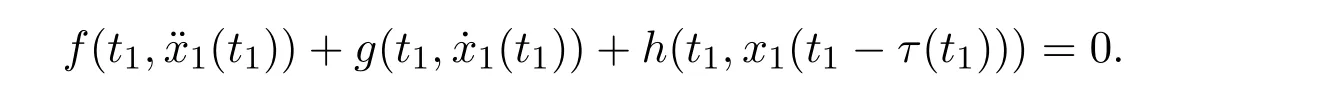
Thus by(H1)and(H2)we have

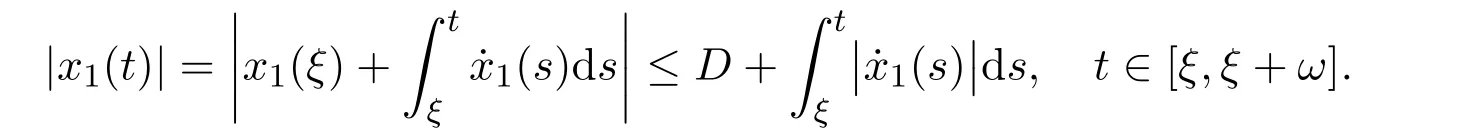
And

Combining the above two inequalities,we obtain

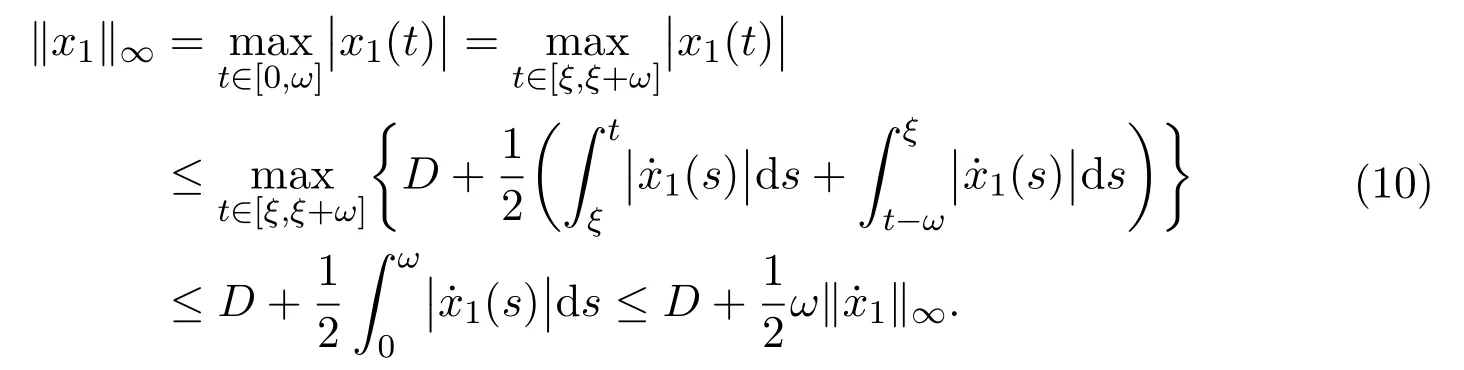
Since x1(0)=x1(ω),there exists a constant η∈[0,ω]such that.Hence

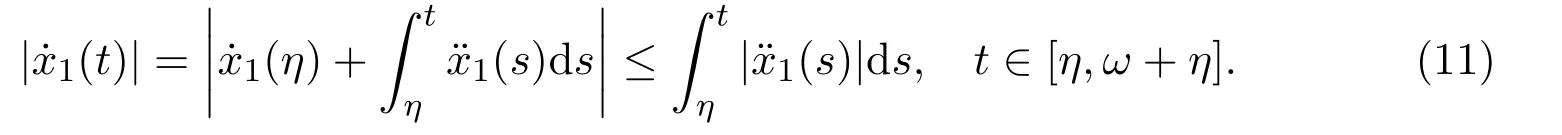
Also

From the above inequalities we have

From the definition of the operator A,we have

Then from(10)and condition(ii)of Theorem 3.1,we have

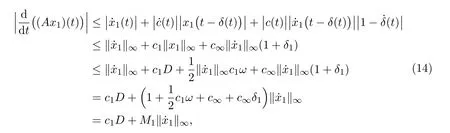
Therefore we get

On the other hand,multiplying both sides of(8)byand integrating it over[0,ω],we get

Hence,we obtain

Therefore from(H4)we have

Using(H1),(H2)and(14)we get

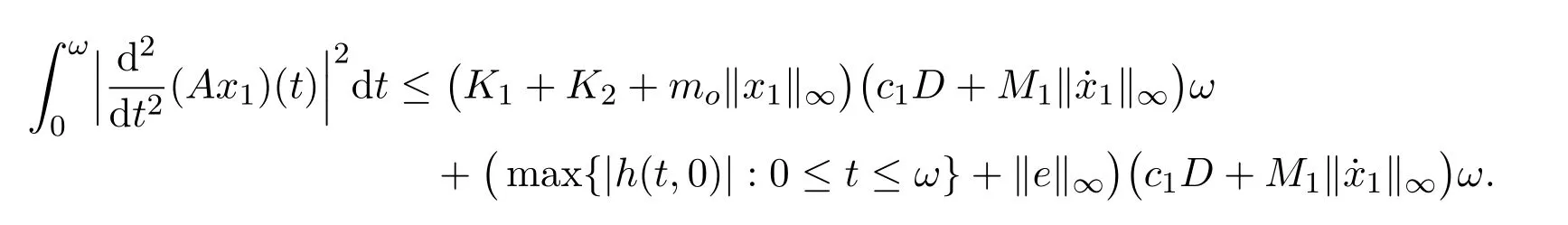
Hence from(10),we obtain

where

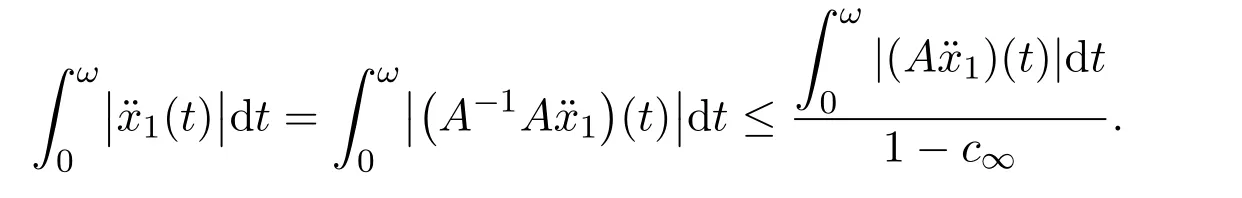
Substituting from(15)and using condition(ii)of Theorem 3.1 we have

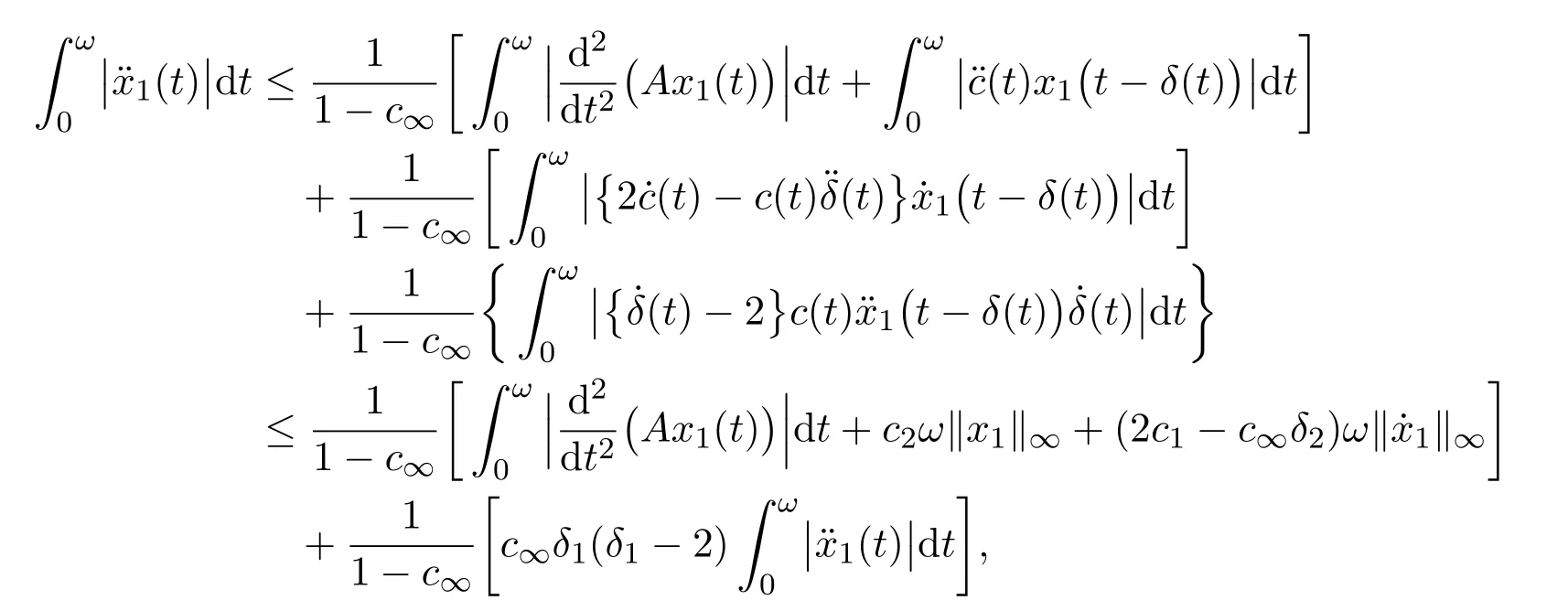
where

From(10)and by Schwarz inequality,we have

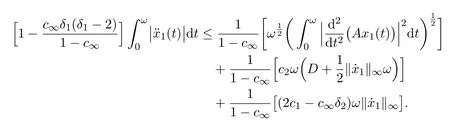
Thus it follows that

Substituting from(13),we get

Therefore we obtain

It follows from(13)that

Thus,from(10)we obtain

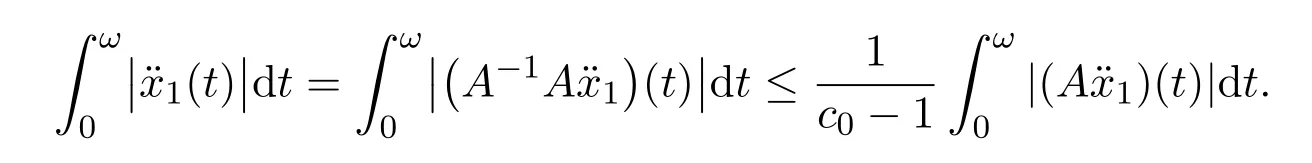
Following the same manner as in Case(i),we can get

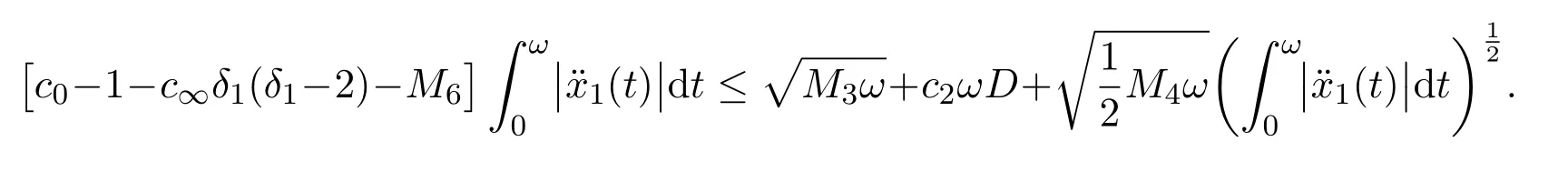
By the first equation of system(7)we have

which implies that there is a constant t1∈ [0,ω],such that x2(t1)=0,hence from(16)we find

In view of Cases(i)and(ii),it is easy to see that there exists a constant M2>0(independent of λ)such that

By the second equation of system(7),we obtain

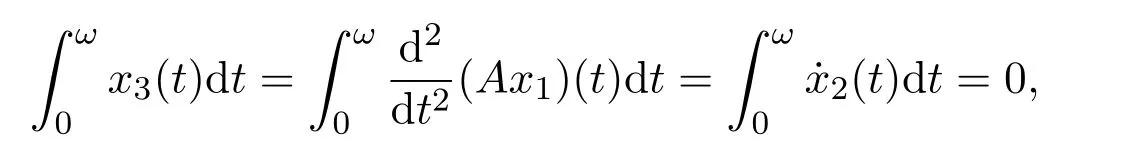
which implies that there is a constant t2∈ [0,ω]such that x3(t2)=0,hence

By the third equation of system(7),we have

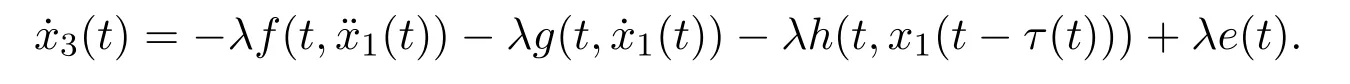
Using(H1),(H2)and(H4),we get

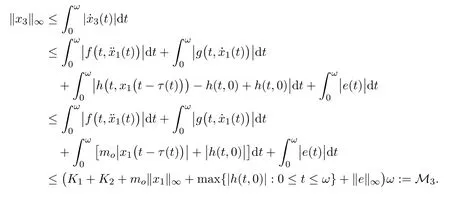
To prove condition(1)of Lemma 3.1,we assume that for any λ∈(0,1)and any x=x(t)in the domain of L,which also belongs to ∂Ω,we must haveFor otherwise in view of(7),we obtain

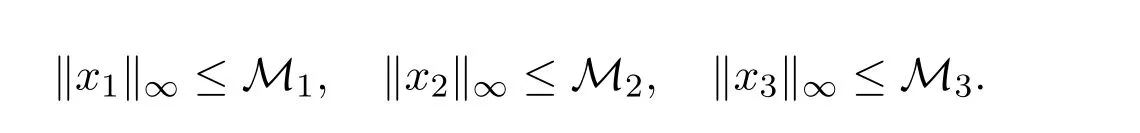
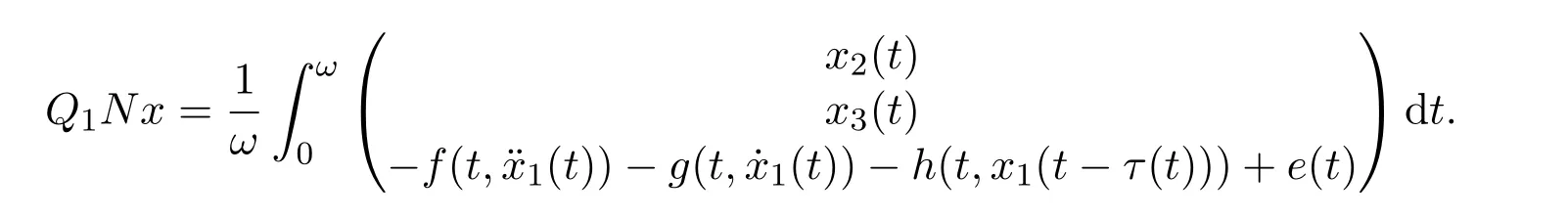
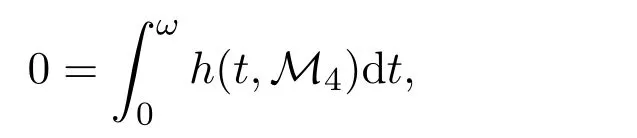
from which there exists a point t2such thatFrom assumption(H3),we havewhich yields a contradiction.Similar analysis holds forTherefore we havehence for all x∈∂Ω∩KerL,so condition(2)of Lemma 3.1 is satisfied.

Define an isomorphism J:ImQ1→KerL as follows:

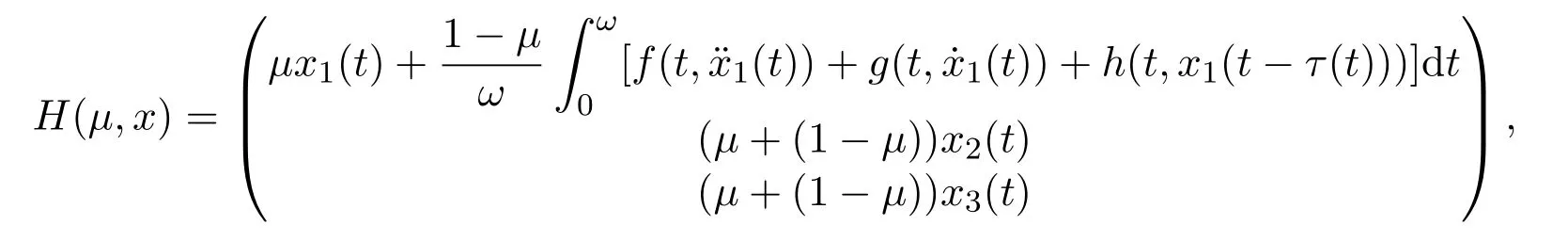
So condition(3)of Lemma 3.1 is satisfied.By applying Lemma 3.1,we conclude that equation Lx=Nx has a solutionthus(1)has an ω-periodic solution x(t).

4 Example

Example 4.1Consider the following third-order neutral functional differential equation:

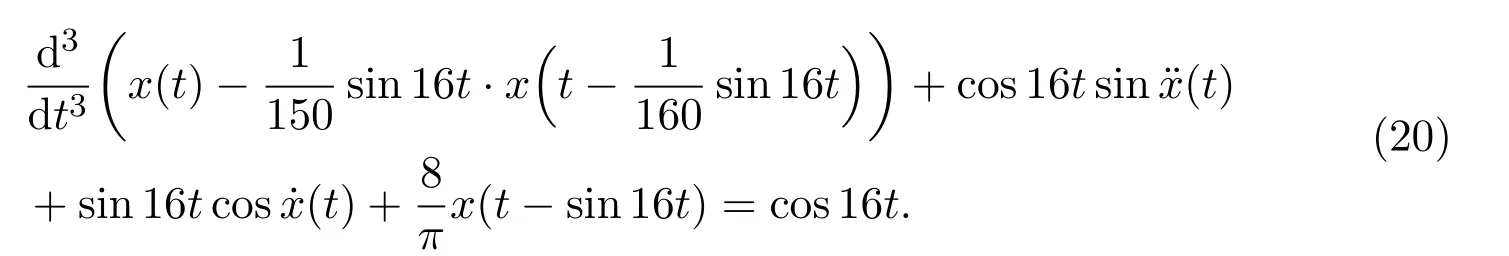
Comparing(20)to(1),we find f(t,u)=cos16tsinu,g(t,v)=sin16tcosv,h(t,x)=sin16t,τ(t)=sin16t,e(t)=cos16t and let

Therefore we get

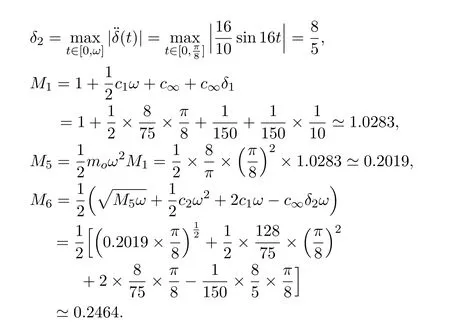
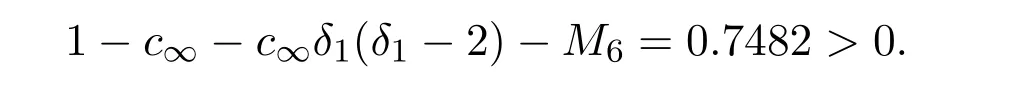
To verify obtain(17),we calculate

Then(17)becomes

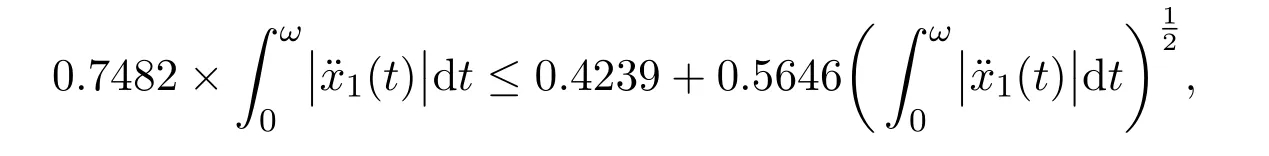
which can be considered as a quadratic inequality,whose roots are

From this,we obtain

The rest of the proof is clear.Hence,by Theorem 3.1,(20)has at least one-periodic solution.