火星着陆器抛背罩分离体气动特性

徐国武，李 齐，周伟江

(1. 中国航天空气动力技术研究院，北京 100074；2. 中国空间技术研究院，北京 100094)

0 引 言

火星着陆任务中，为确保着陆巡视器能安全着陆于火星表面，普遍采用的一种方式是进入、下降和着陆(Entry，Descent and Landing，EDL)方法[1-2]。EDL执行过程包括：巡航段分离、升力式再入、超声速开伞、防热大底分离、背罩分离、着陆平台动力下降与着陆缓冲、空中吊车飞离等。防热大底分离与背罩分离是其中比较关键且容易发生风险的阶段，均属于大钝头分离问题。为了确保分离过程中前体与后体相对运动的安全，除了两者不发生碰撞外，还应包括在规定的高度上两者的相对距离大于最低要求。背罩分离是以形状较为不规整的着陆平台作为前体，比防热大底分离更为复杂一些。

抛背罩过程中，当气流经过着陆平台时，在其背后会形成一个尾流区，在尾流区内靠近着陆平台底部的一段区域内，气流的流动方向与来流方向相反，称为回流区。

当着陆平台与背罩分离后，整个背罩将处于着陆平台的尾流之中，由于回流的作用带给背罩一个向前的吸力，使得着陆平台由阻力产生的减速度大于背罩的减速度。因此，为使着陆平台与背罩能完全分离且不发生碰撞，必须赋予着陆平台一定的初始分离速度，而且着陆平台与背罩还必须具有足够的弹道系数差使得着陆平台下降更快。然而，分离过程中存在很多不确定因素，尤其是在火星大气环境下，很有必要开展背罩分离气动问题的研究。

美国在火星探测方面开展的工作很多[3-6]，其中不乏对分离问题的研究。早期Lang[7]等人曾对海盗号火星巡视器进行过大底分离的风洞试验，后来Behzad[8]等人对试验结果进行了系统的分析，研究了大底与后体的阻力系数随两者之间距离的变化规律，另外，他还通过计算获得了防热大底分离瞬间分离弹簧所产生的推力大小与分离时间的关系[9]。国内虽然在火星探测方面也开展过相关研究，但大多为综述性文章[10-11]或是对EDL方案及技术的分析概括等[12-14]，而并未见到关于背罩分离的相关研究性文献。

基于此，本文将开展背罩分离的定常数值模拟，研究着陆平台与背罩在不同间距情况下的气动特性，分析其中的变化规律，为抛背罩安全性仿真提供必要的支撑。

1 计算模型

由于着陆平台外形十分复杂，开展背罩分离的计算难度较大，为此对背罩分离体做了适当的简化，得到简化模型如图1所示。在此基础上开展背罩分离的定常数值计算，研究分离后着陆平台与背罩之间不同间距情况下各自的气动力系数并进行对比分析，其中，着陆平台与背罩的分离距离可分为轴向距离Δx和侧向距离Δz，如图2所示，作为初步研究，本文只开展不同轴向距离Δx的相关计算分析。

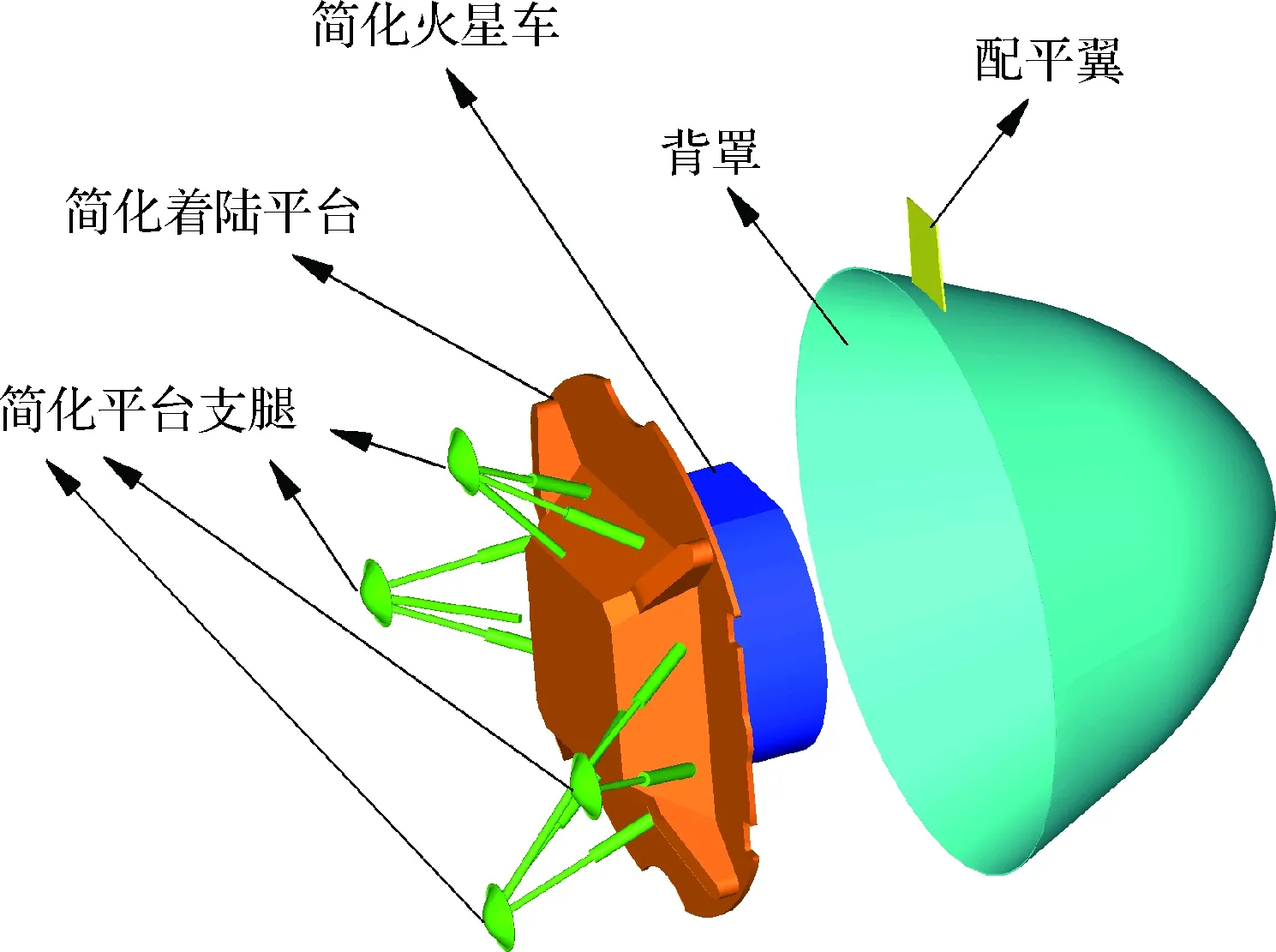
图1 背罩分离体简化模型Fig.1 Simplified model of back shell separator

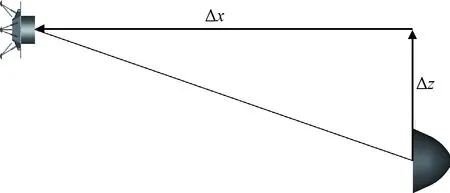
图2 背罩分离距离Fig.2 Back shell separation distance

2 数值方法

2.1 控制方程及计算网格

针对大分离问题，本文计算采用RANS-LES(Reynolds Average Navier Stokes-Large Eddy Simulation)混合方法[15]，它的基本思想是采用RANS高效可靠地模拟高频小尺度运动占主导地位的近壁区域，同时采用LES准确计算低频大尺度运动占优的分离流动区域。由经典的分离涡模拟方法[16-17](Detached Eddy Simulation, DES)改进得到延迟DES方法[18](Delayed Detached Eddy Simulat-ion, DDES)，通过这个方法保护了在附着流边界层的RANS区域计算，同时不会影响在其他区域的DES计算。该方法基于传统的RANS湍流模型方程构造而来。

流场控制方程采用可压缩流粘性气体动力学方程组[19]，具体表述如下：

(1)

(2)

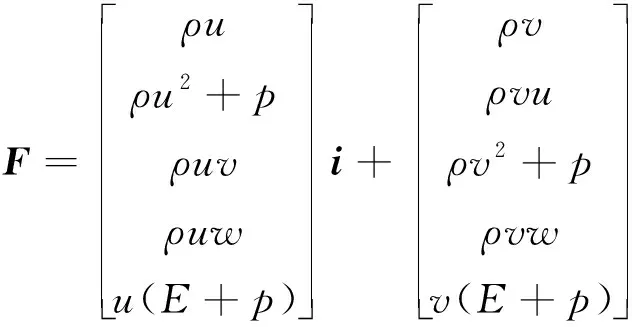
(3)

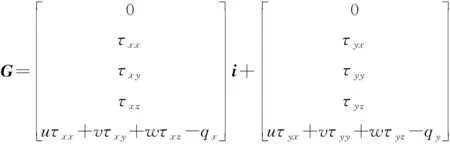
(4)

数值计算网格采用三维自适应笛卡尔网格。这种网格的最大优点是网格生成速度快，自动化程度高，同时完成了黏性边界层网格的划分，使得网格具备粘性模拟能力。

2.2 方法验证

为验证计算方法的可信度，利用神舟飞船返回舱外形进行了典型算例考核。该外形在中国航天空气动力技术研究院FD-12风洞进行过吹风试验，这里针对试验马赫数0.9、单位长度雷诺数1.8×107，采用本文计算方法进行数值计算并与试验结果对比，表1给出了计算轴向力与试验轴向力的比对结果，可以看出，两者误差在2%以内，说明本文计算方法的准确性。

表1 计算结果与试验结果对比Table 1 Contrast of computational result and experimental result

3 分离体气动特性

根据飞行弹道，抛背罩时的分离高度为MOLA(Mars Orbital Laser Altimeter)[20]高度3.387 km，对应的火星大气参数见表2，分离马赫数Ma=0.4，此时火星大气环境下的等效比热比γ=1.29。

表2 火星大气参数Table 2 Mars atmospheric parameter

3.1 抛背罩初始时刻

抛背罩初始时刻，着陆平台与背罩尚未分离，此时两者的轴向力系数如表3所示。可以发现，背罩的轴向力系数远大于着陆平台。这是由于初始分离瞬间，着陆平台嵌入背罩的内部，造成背罩内部不在着陆平台的底部绕流流场内，图3显示了此时两者的压力云图，可以明显发现背罩内部压力接近于着陆平台的前体驻点压力，使得着陆平台前后压差小，因此其轴向力系数很小，而背罩外侧则处于底部绕流的低压区，使得背罩前后压差大，因此背罩轴向力系数远大于着陆平台。

表3 抛背罩初始时刻前后体轴向力系数Table 3 Front and rear of the body axial force coefficient at the beginning of back shell separation

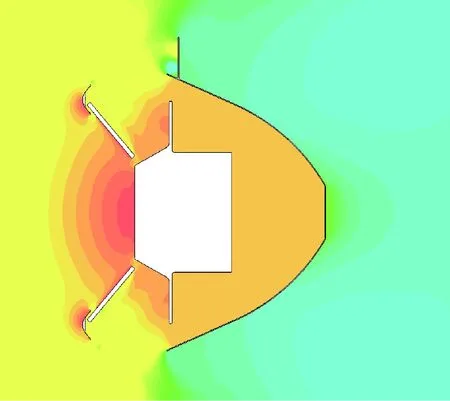
图3 抛背罩初始时刻分离体压力云图Fig.3 Pressure contour at the beginning of back shell separation

3.2 短距分离

抛背罩开始后，随着着陆平台与背罩轴向分离间距Δx的慢慢增加，两者的轴向力系数也将产生变化，为便于分析，轴向距离Δx以火星着陆器大底直径D的倍数给出。图4给出了轴向距离Δx从0D增加到0.1D过程两者的轴向力系数对比。

可以发现，随着轴向分离间距的增加，着陆平台的轴向力系数不断增大，而背罩的轴向力系数则不断减小，变化趋势均呈弱线性，至Δx=0.1D时背罩的轴向力系数变的很小。另一方面，Δx=0～0.06D范围内，背罩的轴向力系数大于着陆平台，说明此时两者的轴向力之差将使得着陆平台下降更快，容易分离；Δx=0.06D～0.1D范围时背罩的轴向力系数已小于着陆平台，此时存在分离后又重新结合碰撞的危险。

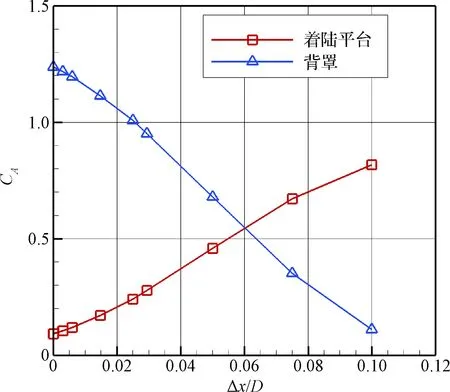
图4 着陆平台与背罩轴向力系数(0～0.1D)Fig.4 Axial force coefficient of landing platform and back shell(0～0.1D)

图5对比了不同轴向距离下的流场压力云图，着陆平台与背罩之间的压力随着轴向距离Δx的增加而逐渐变小，从开始(Δx=0D)的接近驻点压力逐渐变化到后来(Δx=0.1D)的接近底部绕流压力。可以认为，Δx=0.1D是一个突变点，在这之后的很长一段分离间距内，背罩都将处于着陆平台的底部绕流区，因此当Δx>0.1D后，着陆平台与背罩的轴向力系数随分离间距Δx的变化规律也将产生很大不同。

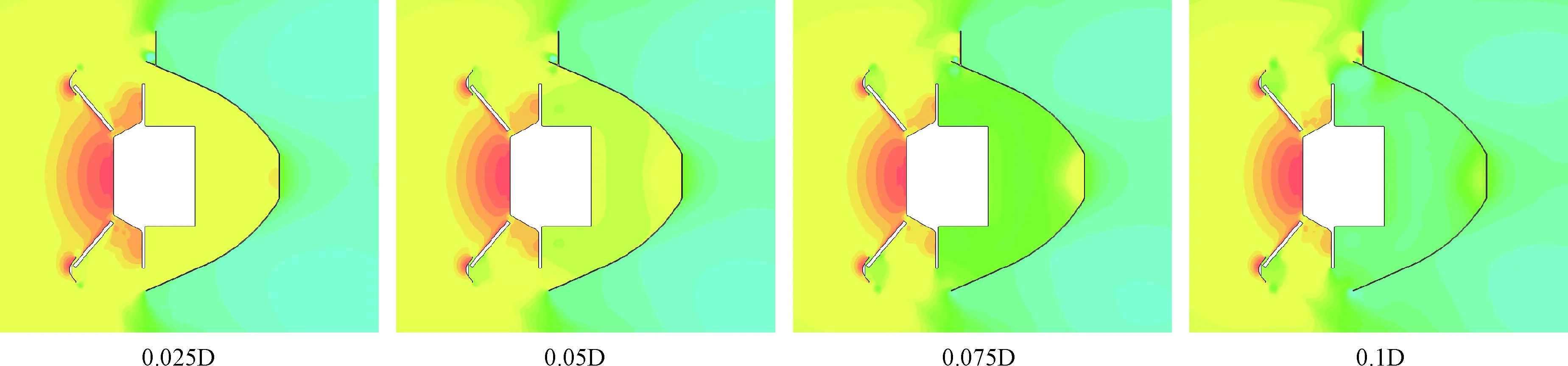
图5 不同轴向距离压力云图对比Fig.5 Contrast of pressure contour at different axial distances

3.3 分离关键区域

图6、图7分别给出了分离间距Δx=0～0.5D及Δx=0～1D范围内着陆平台与背罩的轴向力系数变化情况。可以看出，至Δx=0.1D往后，不管是着陆平台还是背罩，轴向力系数随分离间距的变化规律均发生了很大改变，再一次说明Δx=0.1D是突变点。另外，当Δx=0.5D及Δx=1D时，背罩的轴向力系数变为负值，说明此时背罩受到着陆平台的吸力作用。在此区域内，两者之间产生相互吸引的力，是背罩分离的关键区域。从图8给出的Δx=1D下的流场结构可以看出，着陆平台与背罩之间由于回流作用而产生低压区，从而促使两者之间产生相互吸引的力，这也是此时背罩轴向力系数为负值的原因。需要指出的是，由于背罩外壁上配平翼的存在，外形上下不对称，因此也导致了上下两处分离涡大小存在差异。

3.4 长距分离

图9给出了分离间距Δx=0.1D～10D范围内着陆平台与背罩的轴向力系数变化规律。可以发现，随着分离间距的增加，着陆平台的轴向力系数呈现先增大后减小并最终趋于平稳的趋势，背罩的轴向力系数呈现先减小而后不断增大的趋势。Δx=0.1D～6D范围内，着陆平台的轴向力系数始终大于背罩，在此区间着陆平台与背罩的轴向力之差将使得背罩下降速度更快，存在分离后重新结合并发生碰撞的危险。尤其是在Δx=0.2D～1.8D范围内，背罩的轴向力系数为负值，与着陆平台之间产生吸力，且在Δx=1D时达到峰值，说明Δx=1D时发生碰撞的危险系数最大。Δx>6D之后，着陆平台的轴向力系数变化很小，而背罩的轴向力系数还在不断增大，说明Δx>6D后着陆平台已基本不受背罩的影响，而着陆平台绕流对背罩的影响还在持续。另外，Δx>6D之后，背罩的轴向力系数已超越着陆平台，此时它们的轴向力系数差将促使两者之间越拉越远，可以确保抛背罩安全分离。

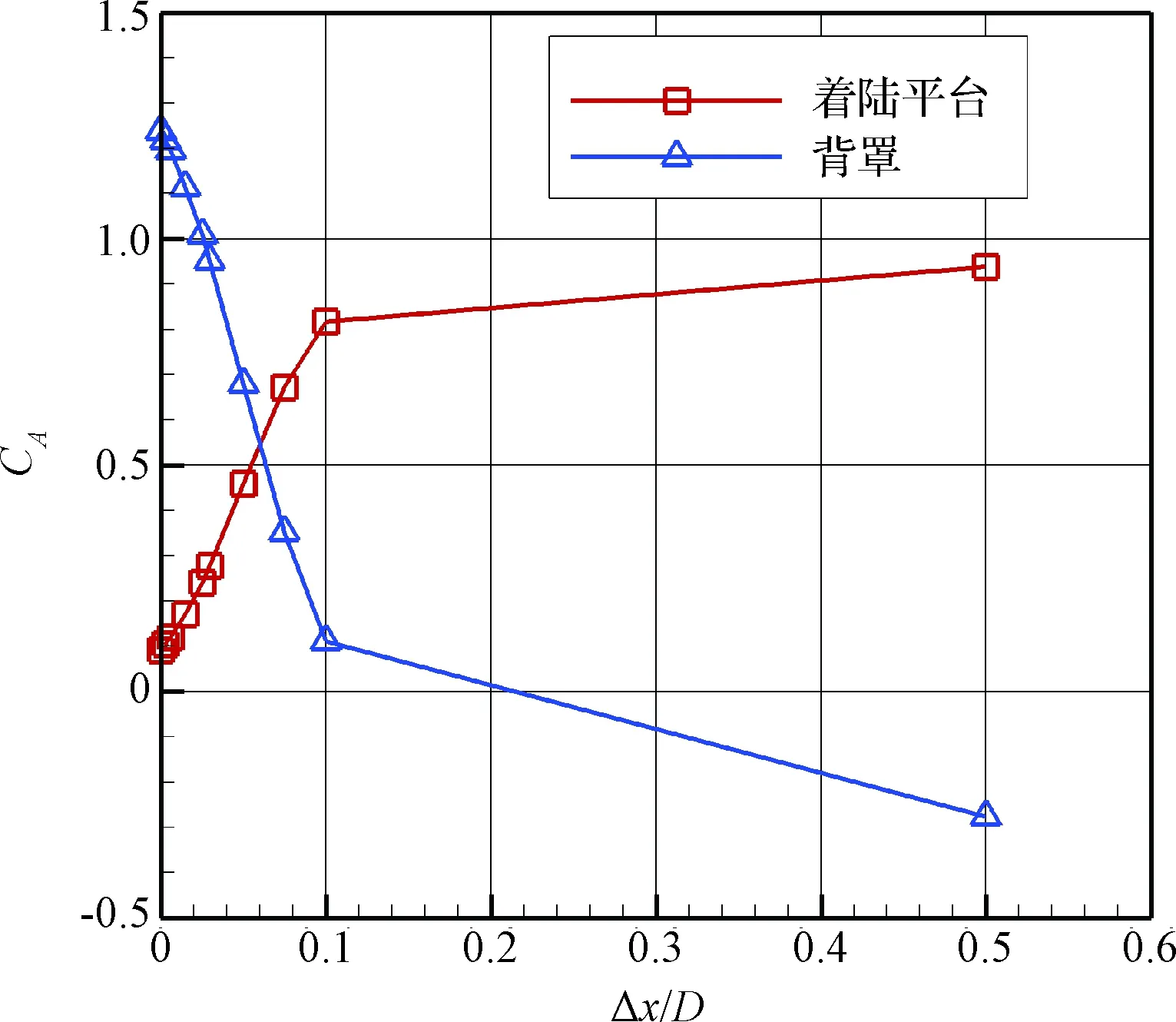
图6 着陆平台与背罩轴向力系数(0～0.5D)Fig.6 Axial force coefficient of landing platform and back shell(0～0.5D)

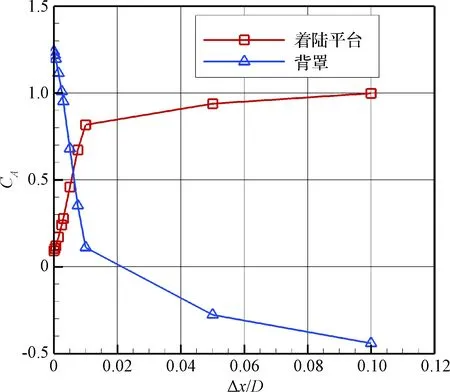
图7 着陆平台与背罩轴向力系数(0～1D)Fig.7 Axial force coefficient of landing platform and back shell(0～1D)

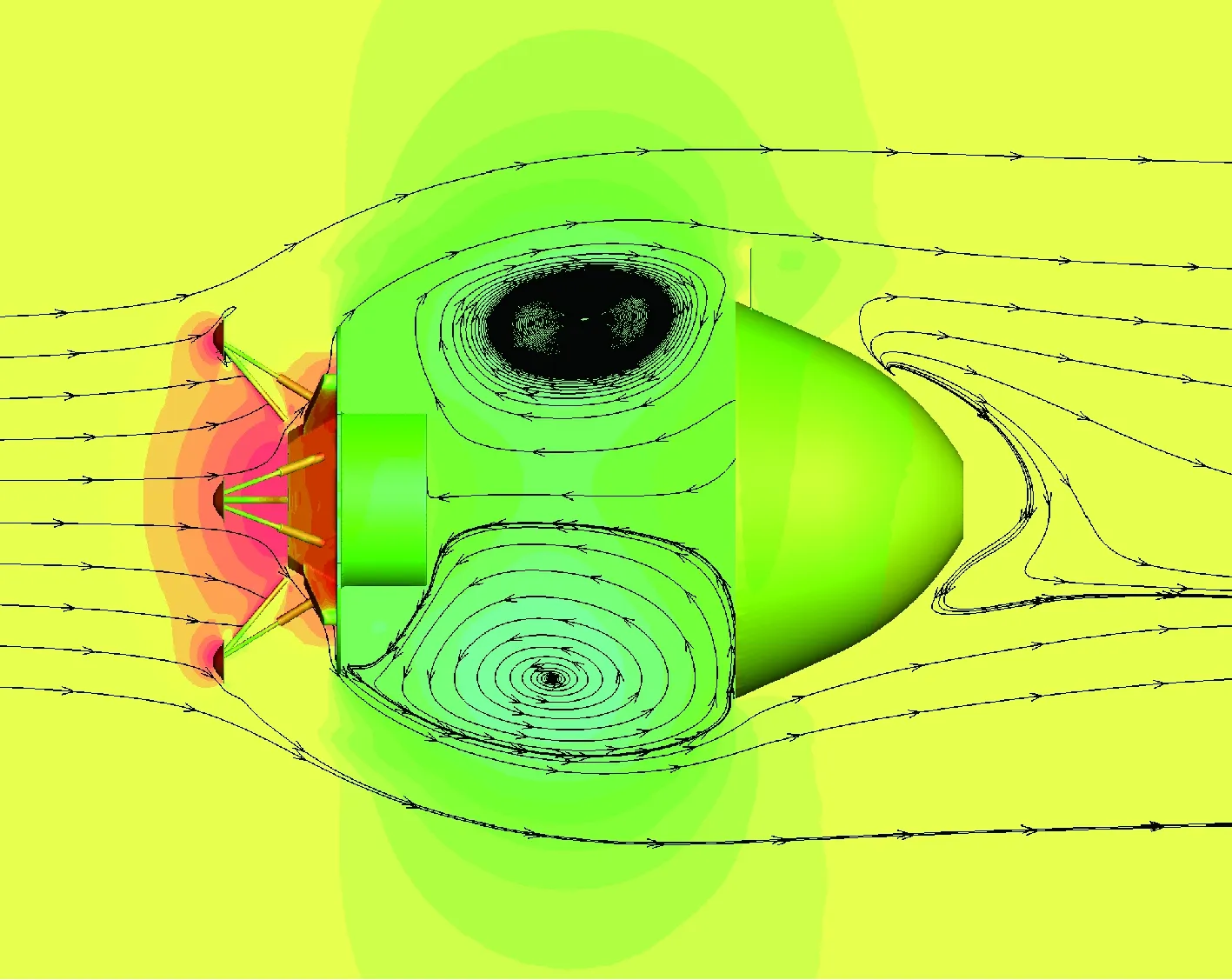
图8 Δx=1D流场结构Fig.8 Flow field structure at Δx=1D

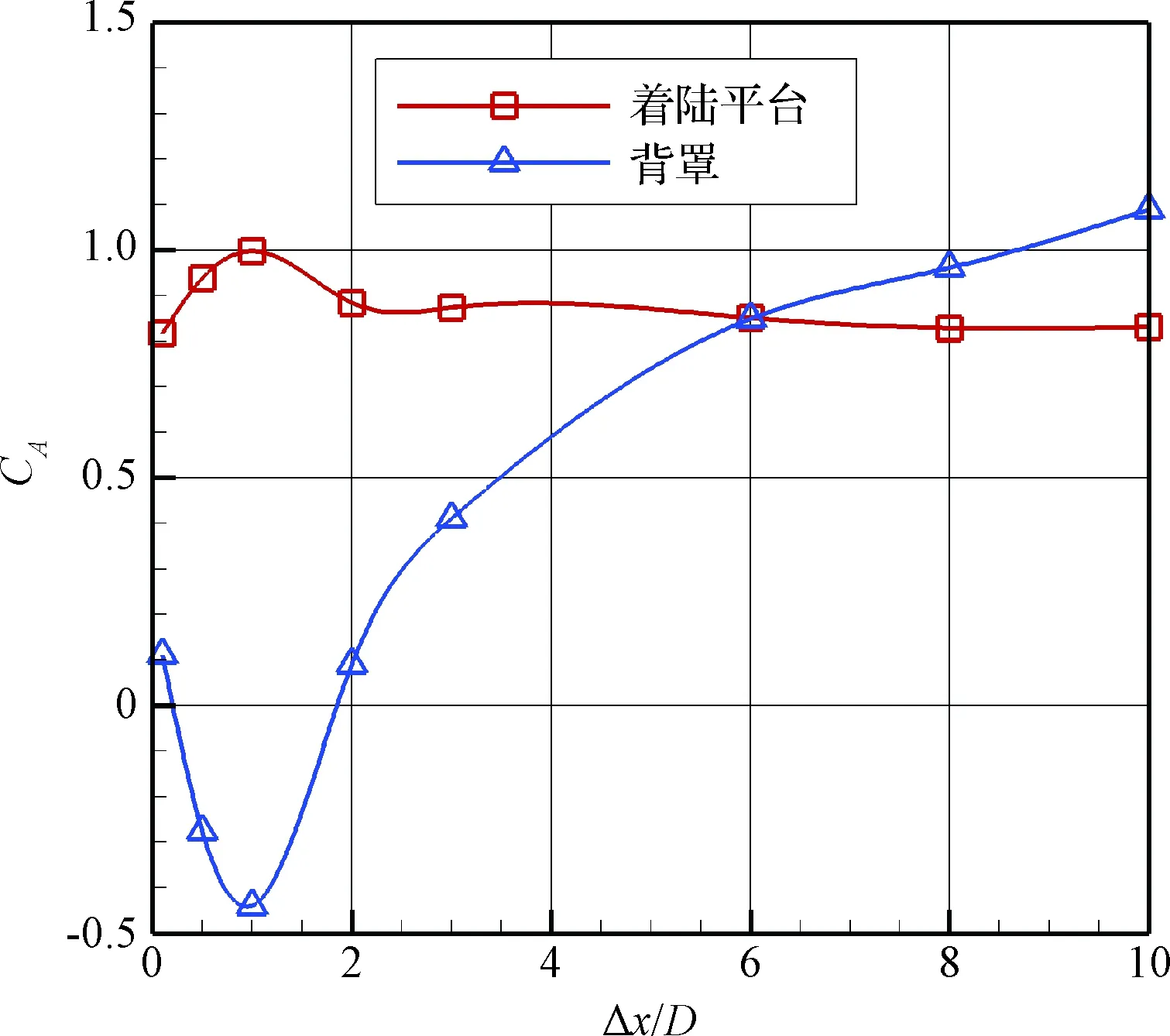
图9 着陆平台与背罩轴向力系数(0.1D～10D)Fig.9 Axial force coefficient of landing platform and back shell(0.1D～10D)

图10给出了Δx=6D时的流场结构，从着陆平台底部两处呈基本对称分布的分离涡，说明此时背罩对着陆平台已基本不存在影响，然而着陆平台底部绕流作用却持续影响着背罩。

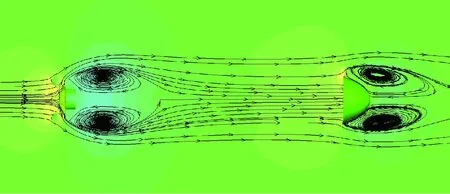
图10 Δx=6D流场结构Fig.10 Flow field structure at Δx=6D

3.5 与文献结果对比

文献[8]针对火星探测漫游者(Mars Exploration Rover, MER)开展过防热大底分离的试验研究工作，图11给出了其试验结果(大底与背罩轴向力系数随分离距离的变化趋势)。MER外形与本文研究的火星着陆器外形均为钝头体外形，两者的气动力作用机理相同，升力主要由轴向力产生，气动特性主要由前体决定，气动特性变化规律相似，气动系数也相当。此外，防热大底分离与背罩分离又都属于大钝头体分离问题，其气动原理相同，因此，可以将MER防热大底分离与本文背罩分离的研究结果进行定性对比。通过比较本文背罩分离的数值计算结果(图9)与文献[8]对防热大底分离的试验结果(图11)，可以看出，分离体(包含前体和后体)的轴向力系数随分离间距的变化规律基本一致，这也从定性上验证了本文对背罩分离数值模拟的准确性。

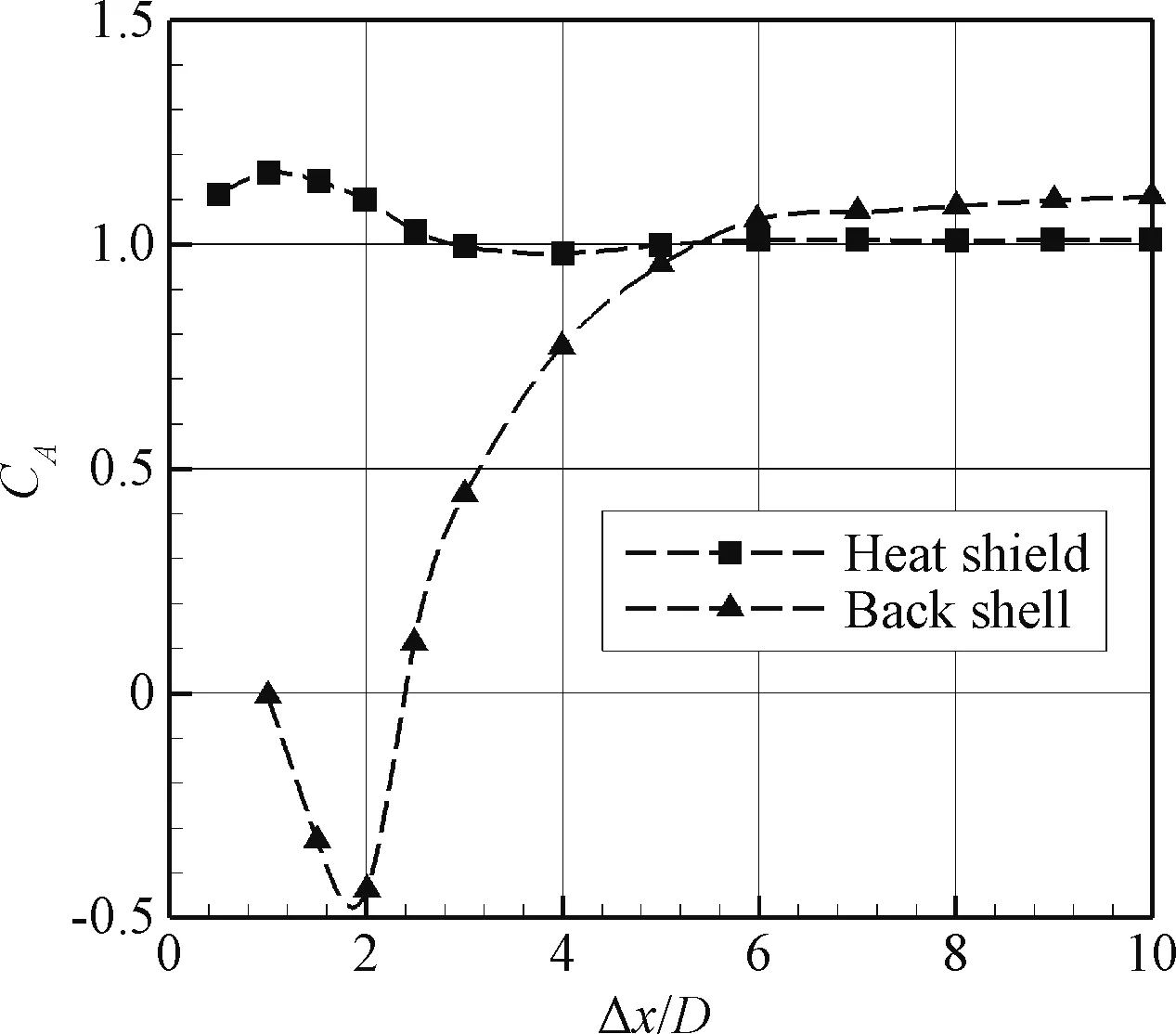
图11 MER外形防热大底分离试验结果Fig.11 Experimental result of MER heat shield separation

4 结 论

基于传统的RANS湍流模型方程构造得到改进的RANS-LES方法，并通过神舟飞船返回舱的算例验证了该计算方法的准确性。通过RANS-LES方法中的DDES方法，采用笛卡尔网格技术对火星着陆器抛背罩分离进行了定常数值计算与分析，获得了着陆平台与背罩轴向力系数随分离间距的变化规律。具体结论如下：

(1)抛背罩初始时刻，背罩的轴向力系数远大于着陆平台。

(2)短距分离(Δx=0～0.1D)，着陆平台的轴向力系数呈弱线性增大，背罩的轴向力系数呈弱线性减小。

(3)Δx=0.1D是背罩分离的突变点。在此之前，背罩与着陆平台之间的压力由接近驻点压力逐渐过渡到接近底部绕流压力；在此之后，背罩将长期处于着陆平台的底部绕流区。

(4)Δx=0.2D～1.8D是背罩分离的关键区域，此时背罩与着陆平台之间产生相互吸引的力，背罩的轴向力系数为负值。

(5)长距分离(Δx=0.1D～10D)，着陆平台的轴向力系数先增大后减小最后趋于平稳，背罩的轴向力系数先减小而后不断增大。

(6)Δx=0～0.06D时，背罩的轴向力系数大于着陆平台，容易分离；Δx=0.06D～6D时，着陆平台的轴向力系数大于背罩，存在分离后重新结合并发生碰撞的危险，Δx=1D时发生碰撞的危险系数最大；Δx>6D后，背罩的轴向力系数再次超越着陆平台，可以确保抛背罩安全分离。

(7)通过与MER防热大底分离的试验结果进行比较，从定性上验证了本文对背罩分离数值模拟的准确性。