高中数学函数分类讨论解题的思考

（湖南广益实验中学 湖南长沙 410019）

引言

分类讨论思想是高中数学解题中极为有效的方法之一，在实际的解题过程中运用这一解题思路，可以进一步实现题目的简化，有利于培养我们的数学解题思维，进一步提高解题效率，在未来的高考中也会发挥很大的作用。

一、分类讨论思想在函数概念解题中的应用

在高中函数概念题型解题时，充分利用函数定义与限制条件，可以更好地进行题目解析。

例1：函数f（x）=ax-x-a（a＞0，且a≠0）含有两个零点，求a的取值范围。

解析：由题意可知函数f（x）含有两个零点，因此可得y=ax和y=x+a之间存在两个交点，通过绘制函数图像可以看出，如果0＜a＜1，则y=ax和y=x+a之间只有一个交点，与题目条件不符；如果a＞1，y=ax图像经过点（0，1），直线y=x+a存在一个高于（0，1）的y轴交点，因此两个函数存在两个交点，a的取值范围为a＞1。

该题是高中数学函数的典型题目，除此之外，还有许多数学概念类题目可以通过分类讨论来解决，比如直线斜率问题、指数函数与对数函数问题等。在进行相关题目的解析时，需要对数学概念进行有目的地分类，以更好地解答相关问题。

二、分类讨论思想在函数图形解题中的应用

运用分类讨论思想解析函数问题时，还可以基于函数的对称轴位置变化、图像变化、斜率变化与交点变化来解答数学函数题型。

例2：xOy平面上，存在曲线y2=2x，存在点A（a，0），其中a∈R。在y2=2x的曲线上，存在点M与点A之间距离最短，其距离为f（a），求取f（a）的表达式。

解析：设曲线y2=2x（x≥0）中存在任意点M（x，y），

三、分类讨论思想在题目运算需要中的应用

高中数学函数题目中，许多题目基于运算的需要，会应用到分类讨论思想，如函数单调性问题中确定导数为正数或负数的问题等[1]。

（1）求取该函数f（x）的值域；

在第一问中，首先可以对值域进行分段求取，最后求其并集。对第二问中的取值范围进行分类讨论，将之分成a＞0，a=0，a＜0三种情况进行讨论来解析题目。

解析：（1）如果x∈[-2，-1），则在[-2，-1）上，为增函数，则

（2）当a=0的情况下，g（x）恒为-2，当且仅当x1∈[-1，1/2）时，f（x1）=g（x0）=-2，不满足题设；

当a＞0的情况下，g（x）=ax-2为[-2，2]上的增函数，且g（x）∈[-2a-2，2a-2]。任意给出的x1∈[-2，2]，

如果存在x0∈[-2，2]，能够成立g（x0）=f（x1），

当a＜0的情况下，g（x）=ax-2为[-2，2]上的减函数，且g（x）∈[2a-2，-2a-2]，

综合以上论述：

四、分类讨论思想在二次函数解题中的应用

1.动轴定区间的二次函数

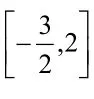
在题目中，可根据题意将其划分为a=0，a≠0两种不同情况进行讨论，通过这种方式可以将题中函数变为一次函数与二次函数，并有差别地对其进行讨论。而二次函数又可以划分为a＞0与a＜0两种不同情况，按照两种情况进行函数图像绘制，基于区间端点数值以及对称轴情况进行分类讨论。在这个过程中，最为关键的环节，是对称轴与区间位置的讨论，以避免重复讨论。

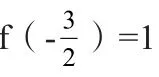
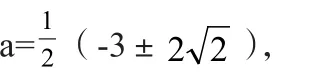
2.定轴动区间的二次函数

针对这一类型的二次函数，其重点在于通过对对称轴在定义域区间位置的讨论来解决该类题型[2]。

结语

分类讨论思想的有效应用，对于我们高中生的思维缜密性提出了较高的要求，在运用的过程中可以有效提高数学思维水平，进一步实现数学题型的化繁为简，确保数学题目的解析更加精准而高效。因此对于我们高中生来说，学会分类讨论解题思想，熟练掌握分类讨论解题思维并在接下来的数学题目解析中加以应用是极为重要的。