加权Motzkin数的恒等式及其组合意义

辛华,杨胜良

(兰州理工大学理学院,甘肃 兰州 730050)

1 引言

以简洁地描述Motzkin路的概念开始.定义n阶的Motzkin路是这样的路,它是指在平面直角坐标系的第一象限内从原点(0,0)到点(n,0)的格路径,并且允许的步法只能为(1,1),(1,0),(1,−1).在点(n,0)结束的Motzkin路的个数记作Mn并且称作n阶Motzkin数.一个在x轴没有水平步的Motzkin路称为一个Riordan路.在点(n,0)结束的Riordan路的个数称为第n个Riordan数Rn.

大量文献对Motzkin路进行了研究,其中一些文献研究了它和其他组合对象的关系,如文献[1-4].更一般地,文献[4]对水平步着k种颜色的Motzkin路进行了讨论并给出了峰和谷的计数方法,而文献[5]则对水平步和下步分别着d和c种颜色的Motzkin路进行了深刻的研究,文献[6-9]则得到了Motzkin序列之间的一些递推关系.本文主要通过Riordan矩阵的A序列和Z序列计算了水平步、上步和下步加权Motzkin路的矩阵及其逆矩阵,在此基础上得到加权Motzkin路的相关递推关系式.以下对本文中使用到的Riordan矩阵的相关概念做简要介绍.

一个Riordan矩阵

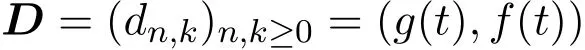
是一个无限下三角形矩阵,它的第k列的生成函数是g(t)f(t)k,即

其中

为形式幂级数,且 g0=1,f0=0,f1̸=0.

2012年,文献[10]引入了Riordan矩阵的概念,本文以引理的形式给出.

引理 1.1 一个 Riordan矩阵 R=(d(t),h(t))可以在文献 [11-13]中分别由两个序列 A=(a0,a1,···) 和 Z=(z0,z1,···) 描述如下:

如果A(z)和Z(z)分别是A序列和Z序列的生成函数,那么就有：

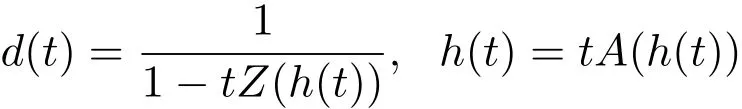
且

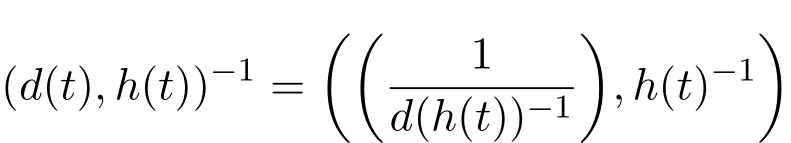
本文的结构如下.第二部分集中讨论了本文的主要结果,在对水平步加权的Motzkin路研究的基础上,利用A序列和Z序列计算出了水平步、上步和下步加权的Motzkin路和Riordan路的矩阵表达式,分别由定理2.1和定理2.2呈现;此外还给出了其逆矩阵的表达式,分别由推论2.1和推论2.2呈现.推论2.2还给出了Riordan矩阵逆矩阵的一般元.第三部分,主要给出了加权Motzkin数的递推关系恒等式并利用二次方程的微分变换给出了证明.

2 加权 Motzkin路与加权 (α,β,γ)-Motzkin数

这一部分将会对不同步加权的 Motzkin路给出组合解释.考虑所谓的 (α,β,γ)-Motzkin路,这种路是水平步有α种颜色,上步有β种颜色以及下步有γ种颜色的部分Motzkin路.用 M(α,β,γ)n(t) 和 R(α,β,γ)n(t) 分别表示在 (n,0) 结束的 (α,β,γ)-Motzkin 路的个数和 (α,β,γ)-Riordan 路的个数,相对应的生成函数分别记作 M(α,β,γ)(t) 和 R(α,β,γ)(t).

根据对非空的(α,β,γ)-Motzkin路的第一个返回点进行分解,所有的这些路都可以通过明确的语法对象构造如图1所示：

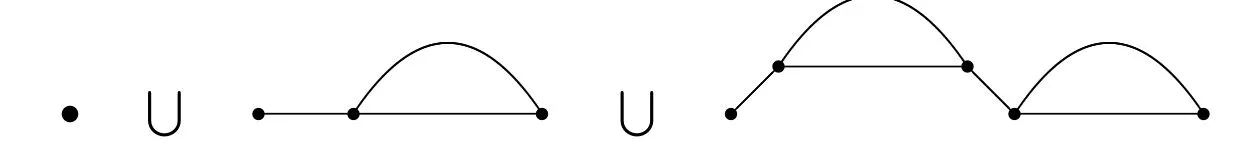
图1 Motzkin路的第一个返回点分解

设

是 (α,β,γ)-Motzkin 路的发生函数,现假设 α,β,γ 固定,且一般将 m(α,β,γ)n记作 mn. 根据上图,则有

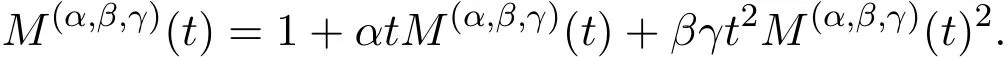
因此 M(α,β,γ)(t)是二次方程 βγt2y2+(αt− 1)y+1=0 的解. 而该二次方程的解是：

其中,由于第一个解不给出非负整数,因此它不可能是加权Motzkin数的生成函数.于是有:

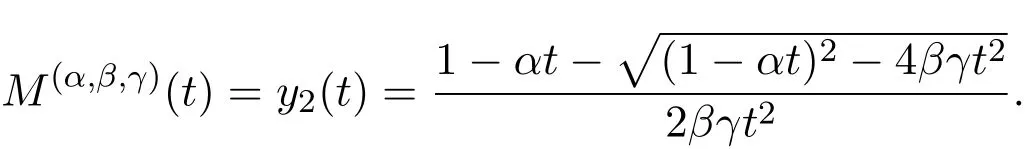
根据对非空的(α,β,γ)-Riordan路的第一个返回点进行分解,所有的这些路都可以通过明确的语法对象构造如图2所示:

图2 Riordan路(在x轴没有水平步的Motzkin路)的第一个返回点分解

故有 R(α,β,γ)(t)=1+ βγt2M(α,β,γ)(t)R(α,β,γ)(t),求解此方程,则可得

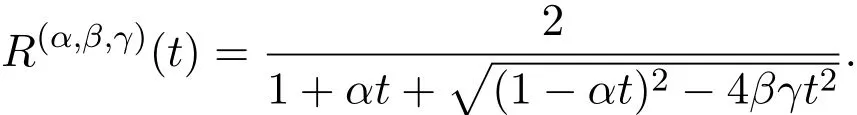
定理 2.1 设Mn,k表示从(0,0)到(n,k)的(α,β,γ)-Motzkin路的个数,则矩阵(Mn,k)n,k∈N是由

给出的Riordan矩阵,其中

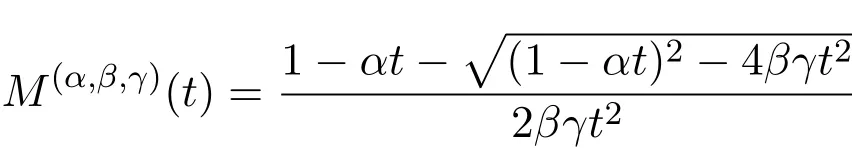
是 (α,β,γ)-Motzkin路个数的发生函数.

证明 因为Mn,k满足以下的递推关系(如图3所示)：

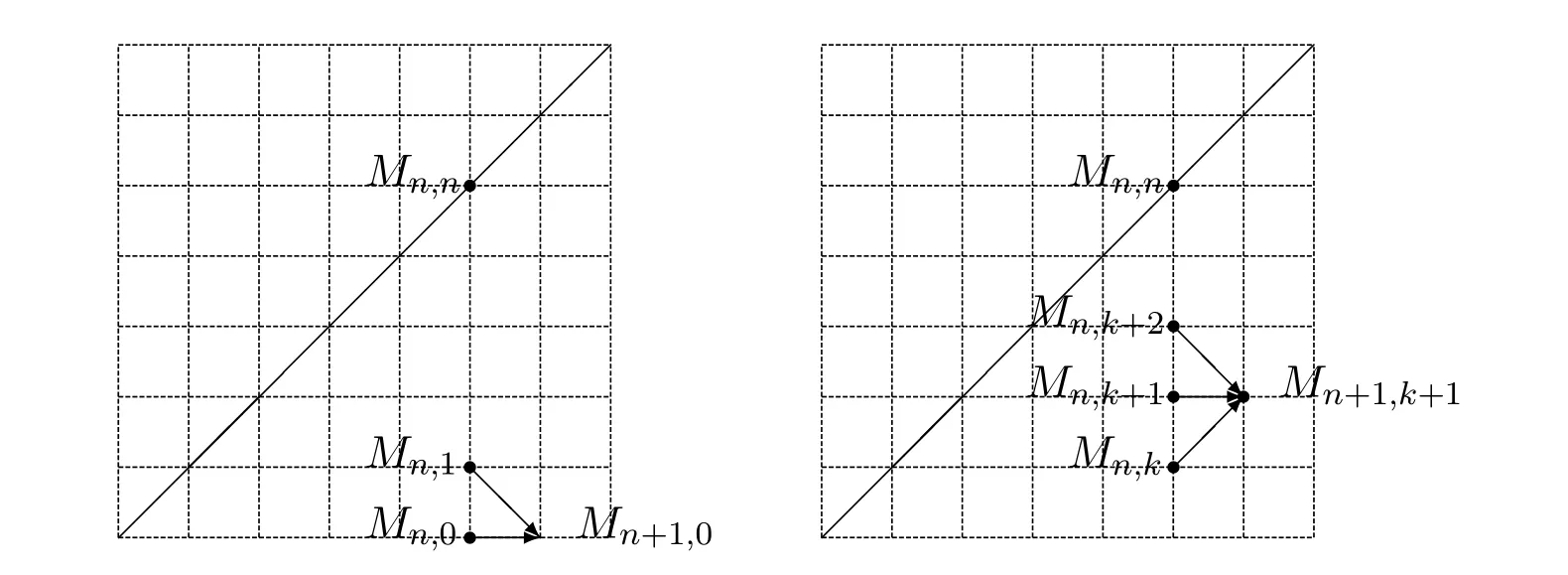
图3 Motzkin路之间的关系

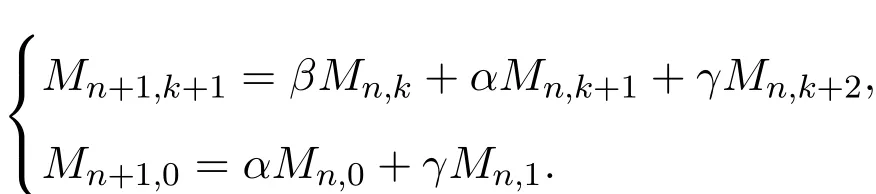
所以

则有

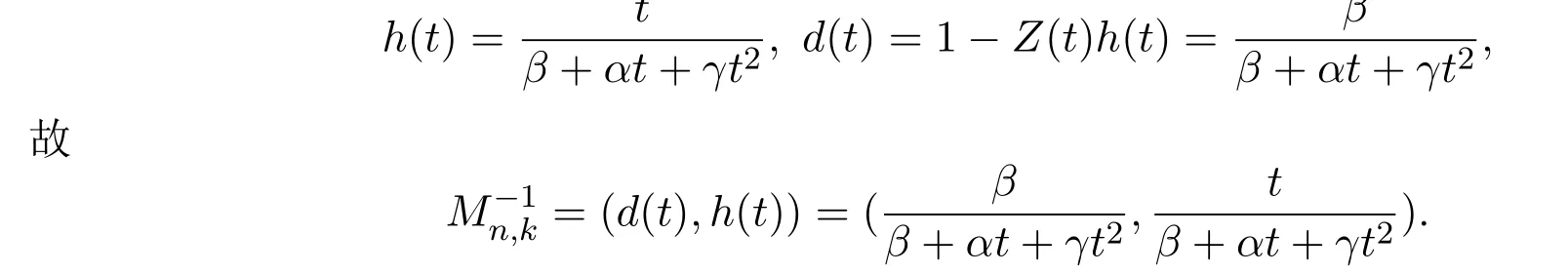
由引理1.1可知,f(t)= ¯h(t),即 h(f(t))=t,则有

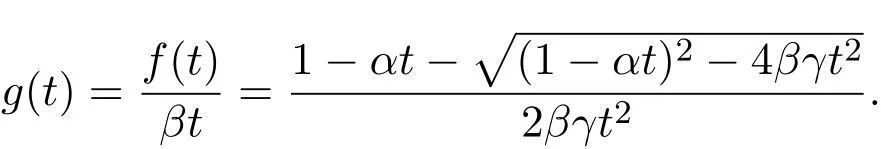
即证

令 ω(t)=tM(α,β,γ)(t),则

利用拉格朗日反演公式,有

推论 2.1 (M(α,β,γ)(t),βtM(α,β,γ)(t)) 的逆矩阵给出如下：

例 2.1 当 (α,β,γ)=(1,1,1),(1,2,1)和 (1,3,1)时,对应的(Mn,k)n,k∈N前几行矩阵如下:

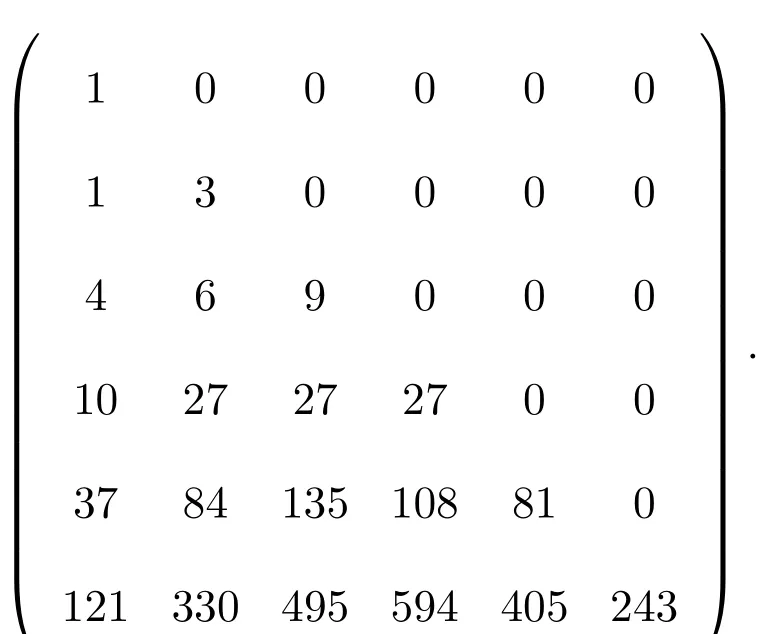
定理 2.2 设Rn,k表示从(0,0)到(n,k)的(α,β,γ)-Riordan路的个数,则矩阵(Rn,k)n,k∈N是由

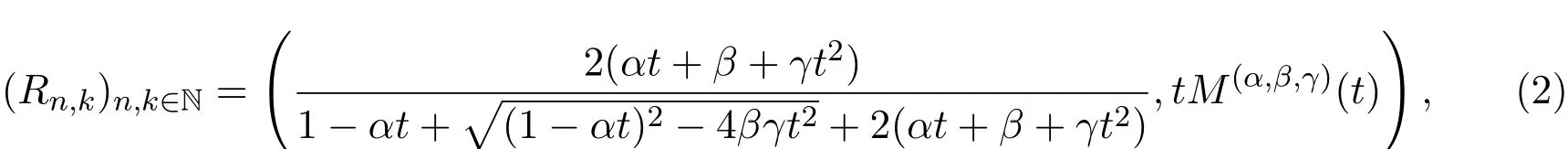
给出的 Riordan 矩阵,其中 M(α,β,γ)(t) 是 (α,β,γ)-Motzkin 路的个数的发生函数.

证明 与定理2.1的证明类似,因此这里省略细节.

推论 2.2(Rn,k)n,k∈N的逆矩阵给出如下:

其中

3 加权 (α,β,γ)-Motzkin数的递推关系

由第 2 部分,可知 (α,β,γ)-Motzkin 路的发生函数 M(α,β,γ)(t) 满足二次方程

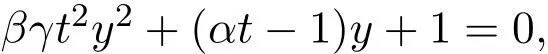
对该方程两边关于t求导,则可得

因此,有

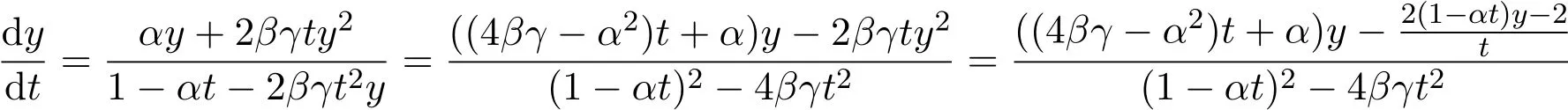
上面最后的等式可以通过交叉相乘然后利用二次方程βγt2y2+(αt−1)y+1=0而得到证明.现在有

可以把上式重新写成

令这个方程左边表达式中tn的系数等于0,其中n≥1,得到

这与文献[4,14]中给出的加权Motzkin数的递推关系式相同,递推关系(4)是非常数系数的2阶齐次线性递推关系.

当 α,β,γ取以下特殊值时,(α,β,γ)-Motzkin数满足不同的递推关系式,而且得到了几个著名的序列:

例 3.1 当α=1,β=1,γ=1时,(1,1,1)-Motzkin数的递推关系式为:

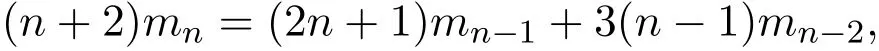
它的前几项是m0=1,1,2,4,9,21,···,这个序列是Motzkin数序列A001006.

例 3.2 当α=2,β=1,γ=1时,(2,1,1)-Motzkin数的递推关系式为:

它的前几项是m0=1,2,5,14,42,···,这个序列是Catalan数序列A000108.

例 3.3 当α=3,β=1,γ=2时,(3,1,2)-Motzkin数的递推关系式为:

它的前几项是 m0=1,3,11,45,197,903,···,这个序列是小 Schr¨oder数序列 A001003.